
A HYBRID GENETIC ALGORITHM FOR THE AIRLINE CREW
ASSIGNMENT PROBLEM
Wagner P. Gomes and Nicolau D. F. Gualda
Universidade de São Paulo, Escola Politécnica, Departamento de Engenharia de Transportes
Av. Professor Almeida Prado, Trav. 2, nº 83, Cidade Universitária, CEP 05508-900, São Paulo, SP, Brazil
Keywords: Air transportation, Airline crew assignment, Metaheuristic, Hybrid genetic algorithm.
Abstract: A typical problem related to airline crew management consists of optimally assigning the required crew
members to flights for a period of time, while complying with labor regulations, safety rules and policies of
the airline. This problem, called the Crew Assignment Problem (CAP), is a combinatorial optimization
problem. Hence, a Hybrid Genetic Algorithm (HGA) associated with a constructive heuristic and a local
search was developed. The HGA was tested and applied to solve instances related to a Brazilian airline.
1 INTRODUCTION
The Crew Assignment Problem (CAP) treated in this
study is defined as the problem of assigning a set of
flights of a given aircraft type to a set of crew
members of the same category (in this case, pilots).
CAP is a combinatorial optimization problem,
making it difficult (or even impossible) to be solved
by exact methods (Barnhart et al., 2003); (Kohn and
Karisch, 2004); (Gopalakrishnan and Johnson,
2005).
Zeghal and Minoux (2006) formulated the CAP
as a large scale integer linear problem. Since feasible
integer solutions could not be reached for some
instances, they proposed a heuristic based on a
rounding strategy embedded in a partial tree-search.
Lucic and Teodorovic (2007) solved real
instances through Simulated Annealing, Genetic
Algorithm and Tabu Search. Souai and Teghem
(2009) proposed a Genetic Algorithm associated
with three local search heuristics to solve CAP.
In this study, a Hybrid Genetic Algorithm (HGA)
is proposed, tested and applied to solve CAP
instances related to a Brazilian airline. Relative to
the research of Souai and Teghem (2009), the
proposed HGA incorporates new mechanisms in the
initial population generation, in the crossover
operator and in the local search.
The paper is organized as follows. In Section 2,
the proposed HGA is describes. Section 3 presents
the results of tests and applications, and Section 4
the conclusions.
2 THE PROPOSED HGA
The input to a CAP is the set of flights to be
covered. Initially, the flights are grouped to form
duty periods that are series of sequential flights
comprising a day’s work for a crew member. Then,
the duty periods are assigned to the crew members,
considering the rules and regulations, the crew
members’ availabilities, and the minimization of
crew total cost.
The rules and regulations applicable to CAP in
the Brazilian context present some specific
constraints, but comply with international ones
(ANAC, 2011); (SNA, 2011).
Each crew member has a personalized calendar
of availability, which takes into account a set of
previously assigned activities. The crew members
receive a fixed salary for 54 flying hours per month
(minimum guarantee) and an additional
remuneration for each exceeding flying hour. As a
quality criterion, the total flying time should be
balanced among the crew members, aiming at the
equalization of salaries.
Figure 1 presents the HGA pseudocode. The
HGA is executed until the number of generations
(Gen) reaches a predefined value (MaxGen). At each
generation, N new solutions (offspring) are
produced, where N is the population size. The
mutation operator is applied with probability Pm to
one of the solutions generated at the crossover. A
local search heuristic (LHS) is applied to the best
solution produced at each generation. A new
190
P. Gomes W. and D. F. Gualda N..
A HYBRID GENETIC ALGORITHM FOR THE AIRLINE CREW ASSIGNMENT PROBLEM.
DOI: 10.5220/0003670601900195
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 190-195
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

population is formed by the best parents and
offspring of the current generation.
function HGA (seed, MaxGen)
1. Build the initial population(Gen=0);
2. While (Gen < MaxGen) do
3. Repeat
4. Select parents for reproduction
(roulette wheel method);
5. Perform crossover;
6. Perform mutation;
7. Apply repair heuristic;
8. Until
(N offspring are created);
9. Evaluate fitness of offspring;
10. Apply local search heuristic;
11. Select the new population (Gen++)
;
12. End While
;
end HGA
Figure 1: The HGA pseudocode.
The following notation is considered:
J
: set of days of the planning horizon (j
J);
K : set of crew members (kK);
F
: set of flights to be covered in the considered
planning horizon (iF);
D : set of all legal duty periods (dD);
j
K
K : set of crew members available to work
on day j
J;
j
FF : set of all flights that start on day j
J;
j
DD : set of all legal duty periods that start on
day j
J;
*
jj
DD : optimal (or initial) set of duty periods
that covers all flights
j
iF exactly once;
k
jj
DD : set of all legal duty periods that can be
assigned to the crew member k on day j, satisfying
all rules and regulations;
dj
F : set of covered flights by duty period
j
dD
on day
jJ ;
nj
Fnc : set of non covered flights by solution n on
day j
J;
nj
Foc : set of over-covered flights by solution n
on day j
J;
nj
Pena : penalty of the solution n related to non
covered and over-covered flights on day j
J, given
by
nj nj nj
Pena Fnc Foc;
n
Pena : penalty of the solution n related to non
covered and over-covered flights, given by
nnj
jJ
Pena Pena
.
2.1 Chromosome Encoding
A matrix
x
()
kj
K
J
Xx
represents the chromosome.
A gene
kj
x
takes value 0 if the crew member k is not
assigned to any duty period on day j (day free),
value -1 if the crew member k is unavailable to work
on day j, or a positive integer value d representing
the code associated to the duty period
j
dD
assigned to crew member k on day j.
The cost of a chromosome n is computed through
expression (1), where
k
c is the cost of the duty
periods assigned to the crew member k, and
k
y is
equal to 1 if the crew member k is used in the
solution n, and zero otherwise.
nkk
kK
Ccy
(1)
The cost of the duty periods assigned to each crew
member k
K is computed through expression (2),
where
1
is the fixed salary of a crew member,
k
D
is the set of duty periods assigned to the crew
member k,
d
f
t is the total flying time of the duty
period d, MG is the minimum guarantee of a crew
member,
2
is the additional remuneration for each
exceeding flying hour, and
d
c is the cost of duty
period d.
12
max 0,
kdd
dD dD
kk
cftMGc
(2)
The cost of a duty period d is computed through
expression (3) and equals the idle time cost of the
crew member plus the overnight rest period cost. So,
is the work cost per minute of a crew member,
elapse is the maximum elapsed time allowed for a
duty period, bt is the brief time,
d
f
t is the total
flying time of the duty period d, dt is the debrief
time, and
c
oc
is the overnight cost in city c.
ddc
c elapse bt ft dt oc
(3)
2.2 Initial Population
The initial population of N chromosomes is built
using a constructive heuristic. It is a simple greedy
approach that sequentially defines the duty period
assignments for the first day of the planning horizon,
then for the second, and so on (day-by-day). This
method is composed of the following steps:
Step 1: Build the optimal (or initial) set of duty
periods
*
j
dD that covers all flights
j
iF exactly
once (duty period determination);
A HYBRID GENETIC ALGORITHM FOR THE AIRLINE CREW ASSIGNMENT PROBLEM
191

Step 2: Build the set of crew members
j
kK
,
and assign the duty periods
*
j
dD to the crew
members
j
kK (duty period assignment).
Initially, a depth-first search procedure on a flight
network is accomplished.
The flight network has a node for each flight
j
iF and arcs representing legal connections
between flights. For each flight node, all legal duty
periods that starts with this flight are enumerated.
Afterward, a model based on set partitioning
problem is considered to determine the optimal set
of duty periods
*
j
dD (expression (4)), where
id
a is
equal to 1 if flight i is covered by duty period d, and
zero otherwise; and
d
y is equal to 1 if duty period d
is included in the set
*
j
D
, and zero otherwise.
*
1,min : , {0,1}
jddiddjd
dD dD
jj
cy i FDayy
(4)
The set partitioning problem is NP-Hard
(Nemhauser and Wolsey, 1999). So, it is very
unlikely that there is an efficient algorithm which
will always solve the problem optimally. Thus, a
strategy based on savings heuristic is also proposed.
The savings heuristic is an adaptation of the
parallel version of the savings heuristic introduced
by Clarke and Wright (1964).
At first, each flight
j
iF represents a duty
period and must be assigned to a distinct crew
member. Next, iteratively, duty periods are merged
based on savings
ij ic cj ij
s
ddd, where
ij
s
is the
savings achieved by merging flights i and j in the
same duty period,
ic
d is the debrief time of flight i in
city c,
cj
d is the brief time of flight j in city c, and
ij
d is the time interval between the flights i and j.
Hence, the number of duty periods
*
j
dD needed to
cover all flights
j
iF on day jJ is reduced.
The duty period assignment is addressed to
produce a legal solution. The pseudocode of this step
is show in Figure 2.
The choice order of the crew members (line 3)
and duty periods (line 6) at each iteration influences
the balance of total flying time among the crew
members. Hence, eight combined alternatives were
proposed for this choice, as shown in Table 1.
function Duty_Period_Assignment (
*
j
D
)
1. Build the set
j
K
;
2. While
( 0
j
K and
*
0
j
D ) do
3. Choose a crew member
j
kK ;
4. Build the set
k
j
D ;
5. If
(
0
k
j
D ) then
6. Choose a duty period
k
j
dD
;
7. Assign the duty period
d to
crew member
k ;
8. Update the set
\
kk
jj
DDd ;
9.
End If
10.
Update the set
\
jj
KKk;
11.
End While;
12.
Update the penalty
nj
Pena ;
end Duty_Period_Assignment
Figure 2: Pseudocode for duty period assignment.
Three distinct strategies were considered, to say,
DET, RAND and GRASP. In the DET strategy, the
first crew member
j
kK
is selected to receive a
duty period d, or the first duty period
k
j
dD is
selected for assignment to the crew member k.
In the RAND strategy, crew members or duty
periods are randomly selected. The GRASP strategy
follows a procedure based on the construction phase
of the GRASP metaheuristic (Feo and Resende,
1995). In this case, a restricted candidate list (RCL)
of the top q crew members
j
kK or p duty periods
k
j
dD is built, where
2
j
qK
and
2
k
j
pD
.
Finally, a crew member k
RCL or a duty period
d
RCL is randomly chosen.
Table 1: Choice of crew members and duty periods.
Alternative Combined strategy
Choice
strategy of
crew members
Choice
strategy of
duty periods
A DET / RAND DET RAND
B RAND / DET RAND DET
C RAND / RAND RAND RAND
D DET / GRASP DET GRASP
E GRASP / DET GRASP DET
F GRASP/ GRASP GRASP GRASP
G GRASP / RAND GRASP RAND
H RAND / GRASP RAND GRASP
The crew members
j
kK
are initially sorted in
an ascending order of priority assignment,
considering two groups: first, the crew members
who have already received some duty period in the
solution, and second, the crew members not used in
the solution. Then, crew members of each group are
reclassified in a total flying time ascending order.
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
192

The duty periods
k
j
dD are sorted in descending
order of number of covered flights
j
iF .
The constructive heuristic does not guarantee the
coverage of all planned flights. In some cases the
crew members can fly as passengers in a duty
period. This type of flight is used to reposition a
crew member to a city, or to enable the crew
member to return to his home base. Consequently,
the fitness of a chromosome n with non covered or
over-covered flights is penalized (see Section 2.3).
2.3 Fitness Function
The fitness function of a chromosome is defined by
expression (5), considered by Souai and Teghem
(2009), where
0,1
n
FF
is the fitness function of
the chromosome n,
n
TC is the total cost of the
chromosome n, and
max
TC is the largest total cost of
the current population.
max maxnn
FF TC TC TC
(5)
The expression (6), adapted from Souai and Teghem
(2009), is used to calculate the total cost of each
chromosome n of the current population, where
n
Pena is the penalty of the solution n related to non
covered and over-covered flights,
n
C is the cost of
chromosome n (expression (1)), and
n
is the
standard deviation function of flying time assigned
to the crew members in the chromosome n.
12
nnnn
TC Pena C
(6)
The parameters
1
and
2
must be adequately
defined to hierarchically minimize the three terms of
the expression (6).
The value of the parameter
1
must ensure that
1
,
nn
Pena C n
.
1
is calculated as follows:
first, the inactive duty period cost is determined;
then a illegal solution is generated, where the
inactive duty period is assigned to the all crew
members k
K in each day jJ; and finally the
value of
1
is determined by expression (7), where
max 1 d
ccJ
is the maximum cost of illegal
schedule assigned to a crew member k.
1max
cK
(7)
The value of
2
is defined through expression (8),
where
1
1,..., . . 0
min
n
nn
nNstC
A
Pena C
and
1,..., . . 0
max
n
nn
nNstC
B
C
.
2
2 if 0,
if 0.
AB A
BA
(8)
2.4 Crossover and Mutation
The crossover operator consists of swapping g genes
1
kj
x
between the selected parents. At this point,
three different crossover strategies were considered,
named as SC (Simplified Crossover), PC
(Probabilistic Crossover), and RC (Random
Crossover). SC and PC strategies were introduced
by Souai and Teghem (2009).
In the SC strategy, a number g is randomly
defined, where
1min,
g
KJ
. Next, g distinct
genes are selected at random, so that two genes are
not selected in the same row k or same column j.
Finally, only the selected genes are swapped.
In the PC strategy, the random selection of g
distinct genes is performed as in the SC strategy.
Next, the selected genes that do not violate the
legality of the solution are automatically swapped.
For other selected genes, the exchange will depend
on the degree of illegality of the solution, measured
by the penalty of day j. More precisely, if
'Xj Xj
P
ena Pena then the exchange is accepted,
where X is the current solution (parent) and X' is the
new solution (offspring). Otherwise, the exchange is
accepted with a probability
1
'
1
Xj Xj
P Pena Pena
.
In the RC strategy, a number g is determined at
random, where
1max,
g
KJ . Then, g distinct
genes are randomly selected, so that two genes can
be selected in the same row k or same column j.
The mutation operator consists to randomly
swapping two genes
1
kj
x
of an offspring.
The legality of the solutions is not assured by the
crossover and mutation operators. Therefore, the set
k
j
D is built for each infeasible gene '
kj
x
. If
k
j
D
then the set of flights
rh
F to be subject to the repair
heuristic is determined. If
rh
F
then the duty
period
k
j
dD that covers the largest number of
flights
rh
iF
and the least number of flights
rh
iF
is assigned to the crew member k on day j.
Otherwise, if
rh
F
then all flights
j
iF are
covered and gene
'
kj
x
is equal to zero. So, the duty
period
k
j
dD
that covers the least number of flights
j
iF
is assigned to crew member k.
A HYBRID GENETIC ALGORITHM FOR THE AIRLINE CREW ASSIGNMENT PROBLEM
193

When a legal duty period is not identified in the
repair heuristic (
k
j
D ), gene
kj
x
removed during
crossover or mutation is restored. Accordingly, the
legality of any solution at the end of the repair
heuristic is ensured.
2.5 Local Search Heuristic (LSH)
A LSH is applied to the best offspring produced at
each generation, in search for a better solution.
Hence, given a solution x*, two neighbouring
solutions x' are explored through two distinct
movements: the reassignment and the exchange
movements.
The reassignment movement consists of
removing a duty period assigned to a given crew
member and then reassigning it to another crew
member available on the same day. The exchange
movement consists of swapping the duty periods
assigned to two crew members on the same day. In
both movements, the selection of days, crew
members and duty periods is done at random.
If one of the neighbouring solutions x' is better
than the solution x*, then x* is replaced by x'. The
illegal solutions x' are discarded.
3 TESTS AND APPLICATIONS
The developed HGA was tested to solve two
instances of the CAP associated to the operation of a
Brazilian airline:
Instance 1: assign 208 flights to 10 pilots for the
period from 02/01/2011 to 02/14/2011;
Instance 2: assign 416 flights to 12 pilots for the
period from 02/01/2011 to 02/28/2011.
The HGA was implemented in C and compiled
using the Microsoft Visual Studio 6.0. The program
was run on a microcomputer PC Intel Core Duo,
1.66 GHz, with 1GB of RAM, under Microsoft
Windows XP - SP3.
The mathematical model used in the duty period
enumeration (Section 2.2) was solved by the linear
programming package CPLEX 11.0 (ILOG, 2007).
The random number generator was the Mersenne
Twister (Matsumoto and Nishimura, 1964).
The HGA was run 10 times for each instance,
with 10 different random seeds (seeds from 1 to 10
on the Mersenne Twister). For each run, it was
considered a maximum of 50,000 generations, a
population of 200 chromosomes, and a probability
of mutation Pm=0.3%.
It is important to emphasize that in the step 1 of
the constructive heuristic both strategies achieved
the same optimal set
*
j
D . Accordingly, these
strategies did not directly influence the HGA results.
Tables 2 and 3 summarize the HGA results for
instances 1 and 2, respectively. The average total
cost value was calculated by
10
1
10
avg w
w
TC TC
,
where
w
TC represents the best total cost value
(expression (6)) obtained in run w .
Table 2: Results obtained by HGA for instance 1.
Initial
population
Crossover
strategy
Average
total cost
(
avg
TC )
Average
CPU time
(seconds)
% Deviation
A
SC 197.52 339 20.44%
PC 194.26 256 18.45%
RC 183.38 405 11.82%
B
SC 228.30 342 39.20%
PC 216.58 267 32.06%
RC 210.77 407 28.52%
C
SC 225.93 319 37.76%
PC 220.72 264 34.59%
RC 213.80 409 30.37%
D
SC 189.85 357 15.76%
PC 179.09 264 9.20%
RC 164.00 426 0.00%
E
SC 202.22 359 23.31%
PC 184.97 262 12.79%
RC 179.52 418 9.47%
F
SC 197.41 386 20.37%
PC 196.82 260 20.01%
RC 177.78 413 8.40%
G
SC 205.10 337 25.06%
PC 201.20 263 22.68%
RC 192.86 400 17.60%
H
SC 227.72 338 38.85%
PC 219.86 279 34.06%
RC 212.63 402 29.65%
Note that the D alternative with random
crossover (RC) produced the best average total cost
value for both instances. Alternatives D, E and F
provided more robustness in the largest instance
(instance 2). In contrast, alternatives A, C and G
showed less robustness for the larger instances.
Predominantly, the RC crossover strategy led to
more effective solutions than other crossover
strategies (SC and PC) for both instances.
The average total cost value as a function of the
association of HGA with the local search heuristic
(LHS) was also evaluated, taking into account the
results obtained for the D alternative combined with
RC crossover strategy (the best one).
Without the association with LSH, HGA achieved
an average total cost of 171.07 for instance 1 (4.31%
higher) and an average total cost of 252.42 for
instance 2 (2.49% higher).
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
194
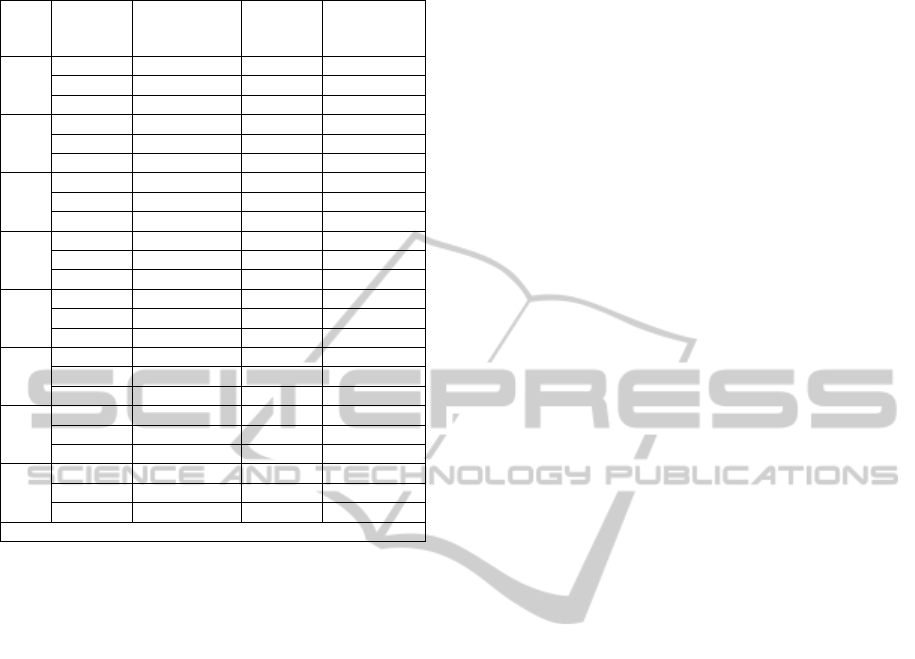
Table 3: Results obtained by HGA for instance 2.
Initial
pop.
Crossover
strategy
Average total
cost (
avg
TC )
Average
CPU time
(seconds)
% Deviation
A
SC 43,035.66* 455 17,374.58%
PC 128,479.62* 387 52,068.99%
RC 85,750.71* 795 34,718.97%
B
SC 393.67 501 59.85%
PC 393.45 407 59.76%
RC 382.21 826 55.19%
C
SC 43,109.16* 480 17,404.42%
PC 391.80 407 59.09%
RC 85,820.74* 821 34,747.41%
D
SC 271.29 570 10.16%
PC 262.67 378 6.65%
RC 246.28 807 0.00%
E
SC 290.57 491 17.99%
PC 288.28 382 17.06%
RC 279.24 813 13.38%
F
SC 279.20 485 13.37%
PC 280.46 377 13.88%
RC 259.47 803 5.36%
G
SC 85,755.44* 468 34,720.89%
PC 85,762.53* 391 34,723.77%
RC 43,040.22* 802 17,376.43%
H
SC 392.97 497 59.56%
PC 393.88 405 59.93%
RC 381.33 823 54.84%
*Solutions where flights were not all covered, resulting in penalty
4 CONCLUSIONS
This study treated the Crew Assignment Problem
(CAP), important part of the airlines operational
planning. A Hybrid Genetic Algorithm (HGA)
associated with a constructive heuristic and a local
search was developed. The HGA yielded feasible
and efficient solutions for the considered instances
with reduced CPU times (order of 8 to 14 minutes).
Elements of the GRASP metaheuristic combined
with a constructive heuristic led HGA to be more
robust and effective. The introduction of the local
search heuristic (LSH) proved to be a way to get
more effective solutions for the CAP. Besides, the
RC (random crossover) strategy proposed in this
study was more effective than other crossover
strategies (SC and PC) found in the literature.
ACKNOWLEDGEMENTS
The authors acknowledge CAPES (Coordenação de
Aperfeiçoamento de Pessoal de Nível Superior),
CNPq (Conselho Nacional de Desenvolvimento
Científico), and LPT/EPUSP (Laboratório de
Planejamento e Operação de Transportes da EPUSP)
for supporting this research.
REFERENCES
ANAC, 2011. Lei do aeronauta (7.183/74). Available at:
<http://www2.anac.gov.br/biblioteca/leis/lei7183%20.
pdf> [Accessed 4 May 2011].
Barnhart, C. et al., 2003. Airline crew scheduling. In: R.
W. Hall, ed.
Handbook of Transportation Science.
Boston: Kluwer Scientific Publishers, p. 1-48.
Clarke, G., Wright, J. W., 1964. Scheduling of vehicles
from a central depot to a number of delivery points.
Operations Research, 12, p. 568-581.
Feo, T. A., Resende, M. G. C., 1995. Greedy randomized
adaptive search procedures.
Journal of Global
Optimization
, 6, p. 109-133.
Gopalakrishnan, B., Johnson, E., 2005. Airline crew
scheduling: State-of-the-art.
Annals of Operations
Research
, 140 (2), p. 305-337.
ILOG, 2007.
CPLEX 11.0 User’s manual. France: ILOG.
Kohn, N., Karisch, S. E., 2004. Airline crew rostering:
Problem types, modeling and optimization.
Annals of
Operations Research
, 127, p. 223-257.
Lucic, P., Teodorovic, D., 2007. Metaheuristics approach
to the aircrew rostering problem.
Annals of Operations
Research
, 155, p. 311-338.
Matsumoto, M., Nishimura, T., 1998. Mersenne Twister:
A 623-dimensionally equidistributed uniform
pseudorandom number generator.
ACM Transactions
on Modeling and Computer Simulation
, 8 (1), p. 3-30.
Nemhauser, G. L., Wolsey, L. A., 1999. Integer and
combinatorial optimization. Wiley – Interscience.
SNA, 2011.
Convenção coletiva de trabalho - 2010/2012.
Available at: <http://www.aeronautas.org.br/images/
stories/convcol/cc_2010_2012.pdf> [Accessed 4 May
2011].
Souai, N., Teghem, J., 2009. Genetic algorithm based
approach for the integrated airline crew-pairing and
rostering problem.
European Journal of Operational
Research
, 199, p. 674-683.
Zeghal, F. M., Minoux, M., 2006. Modeling and solving a
crew assignment problem in air transportation.
European Journal of Operational Research, 175, p.
187-209.
A HYBRID GENETIC ALGORITHM FOR THE AIRLINE CREW ASSIGNMENT PROBLEM
195
