
FUZZY CONNECTEDNESS IN SEGMENTATION OF
MEDICAL IMAGES
A Look at the Pros and Cons
Pawel Badura, Jacek Kawa, Joanna Czajkowska, Marcin Rudzki and Ewa Pietka
Institute of Electronics, Silesian University of Technology, Akademicka 2A, 44-100 Gliwice, Poland
Keywords:
Fuzzy connectedness, Medical image segmentation.
Abstract:
An attempt to recapitulate and conclude numerous experiences with the fuzzy connectedness theory applied
to medical image segmentation is made in this paper. The fuzzy connectedness principles introduced in 1996
have been developed and tested in dozens of studies in past 15 years; many advantages, as well as shortcomings
have been discovered and described. Some aspects of the method and its applications have been summarized
here, including the examples of specific 2D and 3D medical studies with various objects, subjected to fuzzy
connected segmentation. Deliberation about the usefulness of multiseeded and multiobject variants is also
present. An algorithm optimized for matrix computations-based programming languages is introduced. Fi-
nally, 3 fuzzy connectedness-based computer aided diagnosis systems are described and evaluated.
1 INTRODUCTION
There are plenty of areas in the wide world of fuzzy
computations. One of them is the fuzzy connected-
ness (FC) theory, taking advantage of basics of fuzzy
logic, sets and relations. Defined as a methodology
operating on multidimensional and multifeature sets
of ordered and connected data, FC is suited for im-
age processing, in particular for image segmentation.
Segmentation is a process of partitioning an image
into multiple, separate objects – sets of image points,
like pixels or voxels, depending on image dimension-
ality. The points classified into single objects are
strongly connected to each other by some more or less
abstract relations, whilst their relations to points con-
stituting other objects have relatively lower values. If
the features associated with the points are multival-
ued (e.g. grayscale images, like in most medical im-
ages and volumes, taken from Computed Tomogra-
phy CT, Magnetic Resonance MR or Ultrasonography
USG studies), then the fuzzy computations seem to be
perfect in an advanced analysis. For this reason im-
age processing researchers in past decades willingly
introduced some fuzziness into their job.
The point of view that can be taken on such a topic
is twofold: (1) FC method applied to a specific task of
image segmentation or (2) image segmentation per-
formed by a specific tool – FC. Anyway, this paper
comprises a broad look at the fuzzy connectedness in
the segmentation of medical images. After a short re-
view of FC fundamentals, an analysis of character-
istic segmentation subjects is performed, with some
notes on FC variants. Then, the dimensionality and
computational complexity is taken into consideration.
An algorithm optimized for Matlab
r
applications is
proposed. Finally, after a brief presentation of 3 com-
puter aided diagnosis (CAD) systems along with re-
sults obtained at the evaluation stage, some conclu-
sions are made.
2 FUZZY CONNECTEDNESS
The idea of fuzzy connectedness relies on performing
soft computations in digital spaces. The basic work
(Udupa and Samarasekera, 1996) provides definitions
of multiple fuzzy relations within topologically or-
dered dataset C, in particular the fuzzy affinity κ:
κ = {((c, d), µ
κ
(c, d)) | c, d ∈ C×C}, (1)
where µ
κ
∈ [0, 1] is the fuzzy affinity membership
function, and c, d are spels (spatial elements) in C.
If C is a set of image points, then c and d might be
treated as pixels or voxels. The value of µ
κ
is based
on the c and d features, like coordinate adjacency,im-
age intensities I(c), I(d) or local intensity gradients.
Fuzzy affinity has to be reflexive: µ
κ
(c, c) = 1 and
486
Badura P., Kawa J., Czajkowska J., Rudzki M. and Pietka E..
FUZZY CONNECTEDNESS IN SEGMENTATION OF MEDICAL IMAGES - A Look at the Pros and Cons.
DOI: 10.5220/0003670904860492
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 486-492
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

symmetric: µ
κ
(c, d) = µ
κ
(d, c) for all c, d ∈ C. It is
mostly used in the form of:
µ
κ
(c, d) = µ
α
(c, d) · g(µ
φ
(c, d), µ
ψ
(c, d)) (2)
with µ
α
being the functional form of adjacency rela-
tion α (e.g. hard 6-neighbourhoodin a 3D or 4-neigh-
bourhood in a 2D image) and µ
φ
, µ
ψ
– the intensity-
based, and intensity gradient-based parts of the affin-
ity, respectively. Several forms of (2) have been illus-
trated and discussed in (Saha et al., 2000). Most of
the studies prefer the weighted gaussian variant:
µ
κ
(c, d) = µ
α
(c, d)
w
1
e
I(c)+I(d)
2
−m
1
2
2σ
2
1
+
+w
2
e
(
|I(c)−I(d)|−m
2
)
2
2σ
2
2
. (3)
m
1
, σ
1
, m
2
, σ
2
are parameters of κ related to the inten-
sities of segmented object; they are often computed
based on the features of seed points and their neigh-
bours. Weights w
1
, w
2
balance the influence of µ
φ
, µ
ψ
,
both being positive and w
1
+ w
2
= 1.
Adjacency relation α causes µ
κ
to be nonzero
only for pairs of neighbouring spels c and d. Such
a pair is called a link, and the value of µ
κ
(c, d) –
its strength. Consequently, a path is any sequence
of spels he
1
, e
2
, ..., e
m
i such that for any i ∈ [1, m− 1]
a pair he
i
, e
i+1
i is a link. It is noted p
cd
if c = e
1
and d = e
m
. The strength of a path is a strength of
its weakest link – the smallest affinity along the path:
µ
N
(p
cd
) = min
i
{µ
κ
(e
i
, e
i+1
)} (4)
Finally, any image spels c and d are fuzzy connec-
ted according to relation K. The membership function
of fuzzy connectedness µ
K
(c, d) is the strength of the
strongest path p
cd
of all the paths between c and d,
forming a set P
cd
:
µ
K
(c, d) = max
p
cd
∈P
cd
[µ
N
(p
cd
)] (5)
FC-based segmentation requires the selection of
seed point o inside an object, and then computation
of fuzzy connectivity scene C
o
for all spels c ∈ C:
C
o
(c) = µ
K
(o, c), (6)
with the unitary connectivity of a seed point:
C
o
(o) = µ
K
(o, o) = 1. The Dijkstra’s Algorithm (Car-
valho et al., 1999) has been proposed to solve such
a specific shortest path problem faster than with the
dynamic programming approach (Udupa and Sama-
rasekera, 1996). It is also valid in case of all multi-
seeded applications (Saha and Udupa, 2001), where
set O of M (M > 1) seed points o
i
is indicated, as well
as in the relative fuzzy connectedness (RFC) methods
(Herman and Carvalho, 2001), (Udupa et al., 2002),
(Ciesielski et al., 2007), (Badura and Pietka, 2007), to
be discussed later in the paper. Nevertheless, if there
is indeed more than a single seed point for the object,
the scene C
O
for a set O is a fuzzy union:
C
O
(c) =
[
o
i
∈O
C
o
i
(c) = max
o
i
∈O
[µ
K
(o
i
, c)]. (7)
The final determination of segmented object might
be done by the binarisation of sceneC
o
with threshold
θ ∈ [0, 1], resulting in binary image O
κθ(o)
:
O
κθ(o)
(c) =
1 ⇔ C
o
(c) ≥ θ
0 otherwise.
(8)
The RFC variant uses the second object, treated as
a background region with its own seed point b, to de-
termine O
κθ(o)
in a rivalry mode. Spel c ∈ C belongs
to an object according to affinity κ and connectedness
K if µ
K
(o, c) > µ
K
(b, c). The above condition leads
to fuzzy connectivity scenes C
o
and C
b
and their com-
parison in a form of a ”division of spoils”.
The list of medical image processing applications,
where the FC method has been used is already long,
yet still far from completion. Let us notice here
just a few segmentation applications: airway trees
(Tschirren et al., 2005), multiple sclerosis (Udupa
et al., 1997), (Admasu et al., 2003), (Kawa and Pietka,
2008), brain cancer (Moonis et al., 2002), lung cancer
(Badura and Pietka, 2008), (Dehmeshki et al., 2008),
bone cancer (Czajkowska et al., 2010), angiography
(Abrahams et al., 2002), colonoscopy (Udupa et al.,
2001). In many cases FC is treated as a part of a wider
methodology, mostly used for fine segmentation. The
authors of this paper have adapted various models of
FC into segmentation of a variety of anatomical struc-
tures. Some examples and an analysis presented in the
following sections are an attempt to point out areas,
where FC provides an effective outcome, mentioning
also applications requiring modifications.
3 SUBJECT ANALYSIS
3.1 Solid & Well Circumscribed Tissues
If an anatomical structure to be delineated features
an intensity distinctly different than the surrounding
regions, most of the well known segmentation meth-
ods may show their best. The above rule refers both
to: the edge detection (because the edges are sharp
enough), and the region-based methods. The FC ap-
proach belongs to the latter, as a particular type of
FUZZY CONNECTEDNESS IN SEGMENTATION OF MEDICAL IMAGES - A Look at the Pros and Cons
487
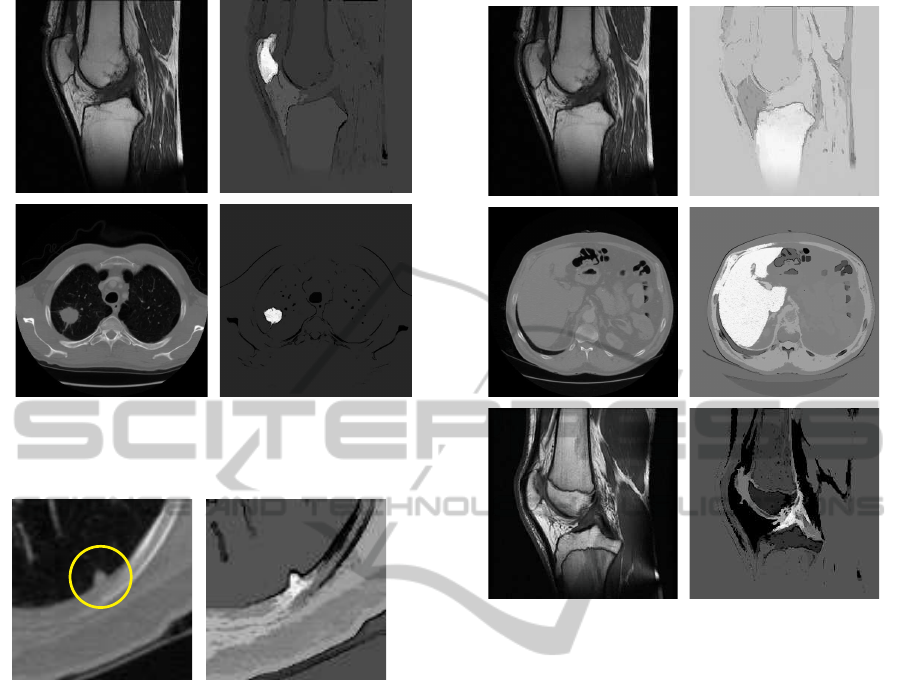
(a)
(b)
Figure 1: Typical well circumscribed objects (left) and their
FC scenes (right). Objects (M – number of seed points):
patella in MR, M = 1 (a), lung nodule in CT, M = 1 (b).
Figure 2: ROI within a thoracic CT with the juxtapleural
lung nodule (left) and its FC scene (right).
a region growing algorithm. In cases of clearly vis-
ible tissues without significant level of noise (or de-
noised by some sort of prefiltering) the canonic form
of FC usually yields very good results. The selection
of threshold θ is quite simple, due to the histogram
bimodality of fuzzy connectivity scene C
o
. Moreover,
such approaches are practically insensitive to the lo-
cation of a seed point, if only located inside an object.
The fuzzy connectivity scenes of a couple of typical
structures are illustrated in Figure 1.
As in all the region growing applications there is
a danger of a ”leak” if there are any ”bridges” be-
tween the object and a region with similar intensity.
Such a problem is visible in case of pleura-connected
lung nodules, where the employment of some prepro-
cessing methods is indispensable (Figure 2).
3.2 Soft Tissues
The fuzziness brought in by the method seems to be
more interesting in difficult cases. Already (Udupa
and Samarasekera, 1996) point out the FC’s good per-
(a)
(c)
(b)
Figure 3: Typical objects more difficult to delineate (left)
and their FC scenes (right): tibia in MR, M = 2 (a), liver in
CT, M = 1 (b), anterior cruciate ligament in MR, M = 2 (c).
formance in the presence of object-independent ”in-
tensity ramps”, mainly due to an enhancement pro-
vided by the gradient-based affinity component µ
ψ
(Figure 3a). Another, yet more frequent example is
a segmentation of regions with slight intensity dif-
ferences, which corresponds to e.g. the abdominal
structures in the CT studies (Figure 3b).
In all cases mentioned above it is advisable to ob-
tain a larger number of seed points, since it leads to
more reliable values of affinity parameters m and σ.
Besides, the computations (growth) of a fuzzy con-
nectivity scene start from many points. If the process-
ing stages preceding the FC analysis are trustworthy
enough, they might even produce full binary masks
corresponding to the core of an object, passed as sets
of seed points to the FC.
Because of the blurred edges between the struc-
tures and therefore less evident slopes in the fuzzy
connectivity scene, the relative FC modes are always
recommended here, despite their greater time con-
sumption. Figure 3c shows the anterior cruciate liga-
ment in a MR slice well separated from the bone, fat
and muscle regions, yet hardly distinguishable from
articular capsule fluids and tissues. Treating the lat-
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
488

Figure 4: ROI within a thoracic CT with the low intensity
lung nodule (left) and its FC scene (right).
ter as a background region with its own seed points
and fuzzy connectivity scene and giving permission
for a ”battle for pixels” usually increases the method
performance.
3.3 Homogeneous vs Inhomogeneous
Regions
Homogeneity of a segmentation subject is a separate
issue, although it refers mainly to the previous sec-
tion. The noise present in the images brings more
problems within the regions, where the intensities
of adjacent structures differ slightly. In the FC ap-
proaches it might lead to leaks or more or less sig-
nificant ”holes” within the fuzzy connectivity scene
region corresponding to an object. Note the liver in
Figure 3b: the inhomogeneity is even more appar-
ent in the fuzzy connectivity scene than in the orig-
inal slice. The image data for the FC analysis should
be prepared, e.g. by the anisotropic diffusion (Per-
ona and Malik, 1990), and additionally postprocessed
e.g. using the mathematical morphology (Gonzalez
and Woods, 2002).
An even more clear example is illustrated in Fig-
ure 4, including an inhomogeneous, vascular lung
nodule with very low intensity. The vessel is sepa-
rated well enough; the lung parenchyma, however, is
not. Thresholding the scene could make binary object
O
κθ(o)
torn or expanded. It is a perfect case to em-
ploy the RFC with a seed point somewhere within the
parenchyma and determine the boundary between the
object and the background by comparing two scenes.
Compare this boundary-setting mechanism to the wa-
tershed algorithm (Gonzalez and Woods, 2002).
3.4 Multiseeded and Multiobject
Approaches
As mentioned above, the performance of FC algo-
rithms improves with an increasing number of seed
points (as in each seeded segmentation method). Usu-
ally, the seed points indicate the core of an object.
With many seed points, the mean distance from the
Figure 5: ROI within an abdominal MR slice with the Ew-
ing’s sarcoma (left) and its FC scene (right).
seed to the object boundaries shorten, which avoids
a potential undersegmentation mechanism. On the
other hand, the determination of fuzzy affinity func-
tion parameters (m, σ in (3)), often relies on the fea-
tures of seed points and their neighbours. In case of
a multiseeded approach such a way of computations
makes the parameters better representatives of an ob-
ject, due to averaging phenomenons. However, the
parameters can be estimated using clustering methods
(e.g. Fuzzy c-Means or Gaussian Mixture Models).
The manual indication of multiple seed points
is rarely performed, because the segmentation ap-
proaches should rather be as automatised as possi-
ble. However, ”indication” might be understood as
”getting as a result of some preprocessing opera-
tion”, which actually allows full automatisation. Sev-
eral such solutions have been designed in our re-
search, e.g. automatic selection of multiple seed
points spread within an object via an evolutionary
algorithm (Badura and Pietka, 2007) or passing the
presegmentation-made binary masks as sets of seed
points (Kawa and Pietka, 2008), (Czajkowska et al.,
2010). The exemplary fuzzy connectivity scene re-
sulting from the latter is presented in Figure 5, where
the object region (a Ewing’ssarcoma) is mostly white,
which relates to the connectivity level at 1.0.
If many adjacent objects have to be determined,
the multiobject FC (Herman and Carvalho, 2001)
might be employed, with at least one seed per each of
the M objects. After getting the M fuzzy connectiv-
ity scenes a defuzzifying decision is made, about the
membership of each point: it is attached to the object
with the strongest connectivity value. In particular, if
two objects are taken into consideration, the method is
called relative fuzzy connectedness. At least one seed
is sown in the object, and at least one – in the back-
ground. In our research this mode has been used a lot
of times, many of them involving object-multiseeded
approaches, as described above.
FUZZY CONNECTEDNESS IN SEGMENTATION OF MEDICAL IMAGES - A Look at the Pros and Cons
489

Figure 6: ROI within prefiltered abdominal CT volume with
liver vasculature (left) and corresponding FC scene (right).
3.5 Dimensionality Analysis
The challenge presented by the FC in the image do-
main is connected with the digital space dimensional-
ity. In the 3D analysis, a number of possible paths is
much higher than in the 2D space and analysis time
increases. In our works both, 2D and 3D modes of
the FC have been performed in multiple, indepen-
dent researches. Depending on the segmentation sub-
ject, various hard adjacency relations α have been em-
ployed: 4- or 8-neighbourhood in 2D as well as 6-,
18- and 26-neighbourhood in 3D. The rule is clear in
all the dimensions: the smaller (closer) the neighbour-
hood for fuzzy affinity κ is: (1) the lower the mean
value of fuzzy connectivity scene is, (2) the lower
the possibility of a ”leak” occurrence is, (3) the faster
the computations are. You may find any of these fea-
tures more important than the other. We mostly prefer
smaller neighbourhoods, since they produce good re-
sults in reasonable time.
A similar remark does not have to be made refer-
ring to the µ
κ
form. It practically does not depend on
the image dimensionality, since equations (1)-(8) take
into consideration two points, independently of how
many coordinates they have. So, we did not make any
particular distinction between 2D and 3D µ
κ
-s.
The practical application in a 3D space may also
be complicated by the inhomogeneous dimensions of
a voxel (a cuboid instead of a cube). Mainly, an in-
terpolation is to be performed in the Z-direction to
ensure the FC not to discriminate any axis. However,
we tried to analyse the FC within uninterpolated vol-
umes, achieving proper segmentation results.
A few consecutive slices of the fuzzy connectivity
scene for a 3D segmentation of liver vasculature are
presented in Figure 6.
Due to the increased computation time, testing
various FC-based methods in the 3D medical images
is harder than in 2D. A robust and fast implemen-
tation is necessary that could be easily deployed in
various image segmentation tasks and integrated with
our prototyping environment (currently Matlab). In
the following section an algorithm optimized for such
conditions is presented.
4 MATLAB OPTIMIZED FC
ALGORITHM
In Matlab the standard FC method (Udupa and Sama-
rasekera, 1996), as well as the Dijkstra’s search
algorithm-based version (Carvalho et al., 1999) can
both be implemented. Both these approaches are far
from optimal for direct use in Matlab, as they operate
iteratively on the separate image points.
Matlab is a weakly-typed, interpreted language
optimized for the matrix computation. In Matlab,
an algorithm implemented by means of standard for
loops and indexing can be much slower than the same
algorithm implemented by operations on the whole
matrices. The process of optimization, that replaces
slow element-wise operations by fast matrix-based
ones is in Matlab known as vectorization.
As images are represented as 3D matrices (tables)
with a basic type of floating point or integer num-
ber, the vectorized implementation can significantly
speed processing. The algorithm presented below
uses the basic 3D manipulation functions available:
circshift
,
padarray
and the matrix-wise
min/max
operations. It can process any number of seed points
in parallel, providing all of them has been chosen
within a single processed object. Using the precom-
puted affinity tables (step 4), the operations are sped
up, but if the memory is a critical factor, the affinity
tables can also be recomputed in each iteration.
1. Chose the hard adjacency relation α.
2. Decompose α to the series of shifts s denoting
neighbouring elements (e.g. a 2D 4-connectivity
consists of: (1) one to the left, (2) one to the right,
(3) one to the bottom and (4) one to the top).
3. Preprocess the original image by padding rows,
columns and layers as not to permit for wrapping
the original values in the later steps.
4. Precompute the fuzzy affinity values for each
neighbourhood member (one table T
s
containing
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
490

the affinity values for each α-connected member;
e.g. 4 tables if 4-connectivity has been chosen;
e.g. T
1
for the one to the left).
5. By using circular shift of the precomputed fuzzy
affinity tables ensure, that the element of a new
T
s
(c) denotes the affinity of original spel c with
respect to the s-th neighbour; e.g. for a pixel c =
(c
x
, c
y
) T
1
(c
x
, c
y
) contains µ
κ
(c, d) with respect to
the left pixel d = (c
x
− 1, c
y
).
6. Prepare zeroed matrix C
o
and set all the elements
matching the seed point locations to ones.
7.
repeat
for each Ts
TEMP = min(Co, Ts);
1
Co = max(Co, TEMP);
2
end
while Co changes
where
min
and
max
are the element-wise matrix
operations.
This can be further sped up if the FC is to be used
in the segmentation by thresholding. Each T
s
ma-
trix can be thresholded and
min/max
can be replaced
by the logical
and/or
operations, respectively. Our
experiences show that the proposed implementation
shortens the computation time compared to the clas-
sic Dijkstra search algorithm by a few times.
5 RESULTS
As mentioned above, in most applications the FC
analysis is used as a part of a wider methodology. It is,
however, usually the critical part of the segmentation
step. It is also the case in our research. Let us point
out 3 of our CAD applications with a brief description
and a results summary.
5.1 Multiple Sclerosis CAD
A 2D relative FC has been used in a Multiple Scle-
rosis (MS) CAD system (Kawa and Pietka, 2008).
The FC is used in the second step of segmentation
in the MR FLAIR images (when location of plaques
has already been established). The MS plaques are
visible in the MR as small, confluent lesions. Due
to a low spatial resolution and small differences in
a signal level, it is not always clear, also to the ra-
diologists, where a boundary of a separate lesion is
located. Using the FC permits to set the continuous
1
zero for elements, that have not been reached yet, tested
path strength otherwise.
2
update, if tested path strength is best so far.
border between a normal and affected tissue. The FC
analysis is initiated in regions surrounding previously
segmented lesions, with a standard affinity and auto-
matically estimated parameters. The results are veri-
fied using gold standard images obtained by the expe-
rienced radiologist. The mean sensitivity for various
test sets varies from 83% to 91%.
5.2 Lung Nodule CAD
A 3D FC in a modified relative mode stands for
a main segmentation stage (Badura and Pietka, 2007),
(Badura and Pietka, 2008). It is preceded by the
presegmentation (including the manual selection of
two seed points, determination of the primary bi-
nary masks for the objects and automatic selection
of the sets of seed points) and followed by post-
processing stage (the vessel removal and correction
procedures). The Lung Image Database Consortium
(LIDC) database, containing 23 cases of various pul-
monary nodules, has been used for evaluation (note
Figures 1b, 2 and 4). The CT studies have been de-
scribed by the voxel probability maps, obtained in the
multistage delineation process, involving experienced
radiologists. At the evaluation stage all cases have
been segmented with the various pairs of manually in-
dicated seed points. The mean sensitivities obtained
in the study were 99.94% for the voxels, whose values
in the probability map were equal to 1.0 and 90.94%,
when their values exceeded 0.5. The mean false posi-
tive rate was 0.39%.
5.3 Bone Cancer CAD
A 3D relative FC on the basis of a gaussian mix-
ture model has been used in the Bone Cancer CAD
(Czajkowska et al., 2010). The database consists of
71 examinations of 48 patients with various types of
bone lesions (tumour and tumour-like),grouped into 8
classes, i.a. Osteosarcomas, Ewing’s sarcomas (Fig-
ure 5) and Chondrosarcomas. A total of 118 differ-
ent MR series have been analysed (T1 contrast en-
hanced, T2 with fat saturation, STIR and PD). The
evaluation stage consists of two parts: the model-
based and the radiologist opinion-based verification.
The model-based step has been performed on the ba-
sis of 24 series. The models have been prepared using
segmentation results verified by the radiologist in or-
der to create additional, synthetic volumes. The mean
sensitivity yielded using the model-based evaluation
was 96.05% with specificity at 98.74%. The second
verification step has been performed based on the ra-
diologist opinion. Here, the algorithm worked cor-
rectly in 74.5% of 118 cases.
FUZZY CONNECTEDNESS IN SEGMENTATION OF MEDICAL IMAGES - A Look at the Pros and Cons
491

6 CONCLUSIONS
In the computer aided diagnosis, the image seg-
mentation is often used as a first step in an au-
tomated case analysis. As such, it benefits from
the fuzzy notion provided by the fuzzy connected-
ness. After 15 years since being announced the fuzzy
connectedness-based algorithms appeared in multiple
segmentation applications and programming environ-
ments (e.g. note the specified FC filters in the ITK –
Insight Toolkit – environment). The properly defined
connectedness between points within objects is help-
ful in achieving precise and reliable delineation of the
structures. Sometimes the FC analysis is sufficient as
a standalone segmentation method; other times it pro-
vides just the most accurate part of a larger process.
The spatial relations and fuzziness used in the seg-
mentation step permit better resemblance to the pro-
cessing performed by the human brain and perceptual
system. In our work the fuzzy connectedness proved
to be a powerfull tool; we can conclude, that its fuzzi-
ness improves flexibility of the segmentation process.
REFERENCES
Abrahams, J. M., Saha, P. K., Hurst, R. W., LeRoux,
P. D., and Udupa, J. K. (2002). Three-Dimensional
Bone-Free Rendering of the Cerebral Circulation Us-
ing Computed Tomographic Angiography and Fuzzy
Connectedness. Neurosurgery, 51:264–269.
Admasu, F., Al-Zubi, S., Toennies, K., Bodammer, N., and
Hinrichs, H. (2003). Segmentation of Multiple Scle-
rosis Lesions from MR Brain Images Using the Prin-
ciples of Fuzzy-Connectedness and Artificial Neuron
Networks. In International Conference on Image Pro-
cessing, ICIP 2003, volume 2, pages II 1081–1084.
Badura, P. and Pietka, E. (2007). Semi-Automatic Seed
Points Selection in Fuzzy Connectedness Approach
to Image Segmentation. In Computer Recognition
Systems 2 (Advances in Soft Computing), volume 45,
pages 679–686. Springer-Verlag.
Badura, P. and Pietka, E. (2008). Pre- and Postprocessing
Stages in Fuzzy Connectedness-Based Lung Nodule
CAD. In Information Technologies in Biomedicine
(Advances in Soft Computing), volume 47, pages 192–
199. Springer-Verlag.
Carvalho, B. M., Joe Gau, C., Herman, G. T., and
Yung Kong, T. (1999). Algorithms for Fuzzy Seg-
mentation. Pattern Analysis & Applications, 2:73–81.
Ciesielski, K. C., Udupa, J. K., Saha, P. K., and Zhuge, Y.
(2007). Iterative Relative Fuzzy Connectedness for
Multiple Objects with Multiple Seeds. Comput. Vis.
Image Underst., 107(3):160–182.
Czajkowska, J., Badura, P., and Pietka, E. (2010). 4D Seg-
mentation of Ewing’s Sarcoma in MR Images. In
Information Technologies in Biomedicine: Volume 2
(Advances in Intelligent and Soft Computing), vol-
ume 69, pages 91–100. Springer-Verlag.
Dehmeshki, J., Amin, H., Valdivieso, M., and Ye, X.
(2008). Segmentation of Pulmonary Nodules in Tho-
racic CT Scans: A Region Growing Approach. IEEE
Transactions on Medical Imaging, 27(4):467–480.
Gonzalez, R. and Woods, R. (2002). Digital Image Process-
ing. Prentice Hall, Upper Saddle River, NJ.
Herman, G. T. and Carvalho, B. M. (2001). Multiseeded
Segmentation Using Fuzzy Connectedness. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 23(5):460–474.
Kawa, J. and Pietka, E. (2008). Automated Fuzzy-
Connectedness-Based Segmentation in Extraction of
Multiple Sclerosis Lesions. In Information Technolo-
gies in Biomedicine (Advances in Soft Computing),
volume 47, pages 149–156. Springer-Verlag.
Moonis, G., Liu, J., Udupa, J. K., and Hackney, D. (2002).
Estimation of Tumor Volume Using Fuzzy Connect-
edness Segmentation of MRI. Am. J. Neuroradiol.,
23(3):356–363.
Perona, P. and Malik, J. (1990). Scale-Space and Edge De-
tection Using Anisotropic Diffusion. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
12(7):629–639.
Saha, P. K. and Udupa, J. K. (2001). Fuzzy Connected Ob-
ject Delineation: Axiomatic Path Strength Definition
and the Case of Multiple Seeds. Computer Vision and
Image Understanding, 83(3):275–295.
Saha, P. K., Udupa, J. K., and Odhner, D. (2000). Scale-
Based Fuzzy Connected Image Segmentation: The-
ory, Algorithms, and Validation. Computer Vision and
Image Understanding, 77(9):145–174.
Tschirren, J., Hoffman, E. A., McLennan, G., and Sonka,
M. (2005). Intrathoracic Airway Trees: Segmentation
and Airway Morphology Analysis from Low-Dose
CT Scans. IEEE Transactions on Medical Imaging,
24(12):1529–1539.
Udupa, J. K., Odhner, D., and Eisenberg, H. C. (2001).
New Automatic Mode of Visualizing the Colon via
CT. In SPIE: Medical Imaging, volume 4319, pages
237–243, San Diego, CA.
Udupa, J. K., Saha, P., and Lotufo, R. (2002). Relative
Fuzzy Connectedness and Object Definition: Theory,
Algorithms, and Applications in Image Segmentation.
IEEE Transactions on Pattern Analysis and Machine
Intelligence, 24(11):1485–1500.
Udupa, J. K. and Samarasekera, S. (1996). Fuzzy Connect-
edness and Object Definition: Theory, Algorithms,
and Applications in Image Segmentation. Graphical
Models and Image Processing, 58(3):246–261.
Udupa, J. K., Wei, L., Samarasekera, S., Miki, Y., van
Buchem, M. A., and Grossman, R. I. (1997). Mul-
tiple Sclerosis Lesion Quantification Using Fuzzy-
Connectedness Principles. IEEE Transactions on
Medical Imaging, 16(5):598–609.
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
492
