
HYBRID RULES OF PERTURBATION
IN DIFFERENTIAL EVOLUTION FOR DYNAMIC OPTIMIZATION
Mikołaj Raciborski
1
, Krzysztof Trojanowski
2
and Piotr Kaczy´nski
1
1
Cardinal Stefan Wyszy´nski University, Faculty of Mathematics and Natural Sciences, College of Sciences, Warsaw, Poland
2
Institute of Computer Science, Polish Academy of Sciences, Warsaw, Poland
Keywords:
Adaptive differential evolution, Dynamic optimization, Symmetric α-stable distribution.
Abstract:
This paper studies properties of a differential evolution approach (DE) for dynamic optimization problems.
An adaptive version of DE, namely the jDE algorithm has been applied to two well known benchmarks:
Generalized Dynamic Benchmark Generator (GDBG) and Moving Peaks Benchmark (MPB) reimplemented
in a new benchmark suite
Syringa
. The main novelty of the presented research concerns application of
new type of solution, that is, solution mutated with an operator originated from another metaheuristics. The
operator uses a symmetric α-stable distribution variate for modification of the solution coordinates.
1 INTRODUCTION
Optimization in dynamic environments is a continu-
ous subject of interest for many research groups. In
the case of dynamic optimization the algorithm has to
cope with changes in the fitness landscape, i.e., in the
evaluation function parameters or even in the evalu-
ation function formula which appear during the pro-
cess of optimum search. There exists a number of dy-
namic optimization benchmarks designed to estimate
efficiency of optimization algorithms. Among these
benchmarks we selected two with the search space de-
fined in R
n
to evaluate the differential evolution (DE)
approach and especially the idea of hybrid population
application. DE approach which originated with the
Genetic Annealing algorithm (Price, 1994) has been
studied from many points of view (for detailed discus-
sion see, for example, monographs (Feokistov, 2006;
Price et al., 2005)). The adaptive version of the DE
algorithm (Brest et al., 2006) differs form the basic
approach in that a self-adaptive control mechanism is
used to change the control parameters F and CR dur-
ing the run.
In the presented research we are interested in ver-
ification of the positive or negative role of a muta-
tion operator originating from another heuristic ap-
proach when it is applied in the DE algorithm. The
proposed type of mutation employs random variates
controlled by the α-stable distribution which already
proved their usefulness in other version of evolution-
ary approach and in the particle swarm optimization.
The paper is organized as follows. In Section 2
a brief description of the optimization algorithm is
presented. Section 3 discuss properties of new type
of mutation introduced to jDE. The description of a
new benchmark suite
Syringa
is given in Section 4
whereas Section 5 includes some details of the ap-
plied measure and the range of the performed tests.
Section 6 shows the results of experiments. Section 7
concludes the presented research.
2 THE jDE ALGORITHM
The differential evolution algorithm is an evolution-
ary method with a very specific mutation operator
controlled by the scale factor F. Three different, ran-
domly chosen solutions are needed to mutate a target
solution x
i
: a base solution x
0
and two difference so-
lutions x
1
and x
2
. Then, a mutant undergoes discrete
recombination with the target solution which is con-
trolled by the crossover probability factor CR ∈[0, 1].
Finally, in the selection stage trial solutions compete
with their target solutions for the place in the pop-
ulation. This strategy of population management is
called DE/rand/1/bin which means that the base solu-
tion is randomly chosen, 1 difference vector is added
to it and the crossover is based on a set of independent
decisions for each of coordinates, that is, a number of
parameters donated by the mutant closely follows a
binomial distribution.
32
Raciborski M., Trojanowski K. and Kaczy
´
nski P..
HYBRID RULES OF PERTURBATION IN DIFFERENTIAL EVOLUTION FOR DYNAMIC OPTIMIZATION.
DOI: 10.5220/0003671800320041
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 32-41
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

Algorithm 1: jDE algorithm.
1: Create and initialize the reference set of (k·m) solutions
2: repeat
3: for l = 1 to k do {for each subpopulation}
4: for i = 1 to m do {for each solution in a subpopulation}
5: Select randomly three solutions: x
l,0
, x
l,1
, and x
l,2
such that: x
l,i
6= x
l,0
and x
l,1
6= x
l,2
6: for j = 1 to n do {for each dimension in a solution}
7: if (rand(0,1) > CR
l,i
) then
8: u
l,i
j
= x
l,0
j
+ F
l,i
·(x
l,1
j
−x
l,2
j
)
9: else
10: u
l,i
j
= x
l,i
j
11: end if
12: end for
13: end for
14: end for
15: for i = 1 to (k ·m) do {for each solution}
16: if ( f(u
i
) < f(x
i
) then {Let’s assume this is a minimization problem}
17: x
i
= u
i
18: end if
19: Recalculate F
i
and CR
i
20: Apply aging for x
i
21: end for
22: Do overlapping search
23: until the stop condition is satisfied
The jDE algorithm (depicted in Figure 1) extends
functionality of the basic approach in many ways.
First, each object representing a solution in the popu-
lation is extended by a couple of its personal param-
eters CR and F. They are adaptively modified every
generation (Brest et al., 2006). The next modifications
have been introduced just for better coping in the dy-
namic optimization environment. The population of
solutions has been divided into five subpopulations of
size ten. Each of them has to perform its own search
process, that is, no information is shared between sub-
populations. Every solution is a subject to the aging
procedure protecting against stagnation in local min-
ima and just the global-best solution is excluded from
this. To avoid overlapping between subpopulations a
distance between subpopulation leaders is calculated
and in the case of too close localization one of sub-
populations is reinitialized. However, as in previous
case the subpopulation with the global-best is never
the one to reinitialize. The last extension is a mem-
ory structure called archive. The archive is increased
after each change in the fitness landscape by the cur-
rent global-best solution. Recalling from the archive
can be executed every reinitialization of a subpopula-
tion, however, decision about the execution depends
on a few conditions. Details of the above-mentioned
extensions can be found in (Brest et al., 2009).
3 PROPOSED EXTENSION OF
jDE
The novelty in the algorithm concerns introduction of
new type of solutions into the population of size M. A
small number of new solutions (just one, two, or three
pieces) replace the classic ones so the population size
remains the same. The difference between the classic
solutions and the new ones lies in the way they are
mutated. New type of mutation operator is based on
the rules of movement governing quantum particles in
mQSO (Trojanowski, 2009).
In the first phase of the mutation, we generate
a new point uniformly distributed within a hyper-
sphere surrounding the mutated solution. In the sec-
ond phase, the point is shifted along the direction de-
termined by the hypersphere center and the point. The
distance d
′
from the hypersphere center to the final lo-
cation of the point is calculated as follows:
d
′
= d ·SαS(0, σ) ·exp(−f
′
(x
i
)), (1)
where d is a distance from the original location ob-
tained in the first phase, SαS(·, ·) denotes a symmet-
ric α-stable distribution variate, σ is evaluated as in
eq. (2) and f
′
(x
i
) as in eq. (3):
HYBRID RULES OF PERTURBATION IN DIFFERENTIAL EVOLUTION FOR DYNAMIC OPTIMIZATION
33

σ = r
SαS
·(D
w
/2) (2)
f
′
(x
i
) =
f(x
i
) − f
min
( f
max
− f
min
)
(3)
where:
f
max
= max
j=1,...,M
f(x
j
), f
min
= min
j=1,...,M
f(x
j
).
The α-stable distribution (called also a Lev´y distribu-
tion) is controlled by four parameters: stability index
α (α ∈ (0,2]), skewness parameter β, scale parame-
ter σ and location parameter µ. In our case we as-
sume µ = 0 and apply the symmetric version of this
distribution (denoted by SαS for ”symmetric α-stable
distribution”), where β is set to 0.
The resulting behavior of the proposed operator is
characterized by two parameters: the parameter r
SαS
which controls the mutation strength, and the param-
eter α which determines the shape of the α-stable dis-
tribution. The solutions mutated in this way are la-
beled as s
Lev´y
in the further text.
4 THE Syringa BENCHMARK
SUITE
For the experimental research we developed a new
testing environment
Syringa
which is able to sim-
ulate behavior of a number of existing benchmarks
and to create completely new instances as well. The
structure of the
Syringa
code originates from a fit-
ness landscape model where the landscape consists of
a number of simple components. A sample dynamic
landscape consists of a number of components of any
types and individually controlled by a number of pa-
rameters. Each of the components covers a subspace
of the search space. The final landscape is the result
of a union of a collection of components such that
each of the solutions from the search space is covered
by at least one component. In the case of a solution
belonging to the intersection of a number of compo-
nents the solution value equals (1) the minimum (for
minimization problems) or (2) maximum (otherwise)
value among the values obtained for the intersected
components or (3) this can be also a sum of the fit-
ness vales obtained from these components (not used
in our case). Eventually, the
Syringa
structure is a
logical consequence of the following assumptions:
1. the fitness landscape consists of a number of any
different component landscapes,
2. the dynamics of each of the components can be
different and individually controlled,
3. a component can cover a part or the whole of the
search space, thus, in case of a solution covered
by more than one component the value of this so-
lution can be a minimum, a maximum or a sum of
values returned by the covering components.
4.1 The Components
The current version of
Syringa
consists of six types
of component functions (Table 1) defined for the real-
valued search space. All of the formulas include
the number of the search apace dimensions n which
makes them able to define for the search spaces of
any given complexity.
There can be defined a number of parameters
which individually define the component properties
and allow to introduce dynamics as well. For each
of the components we can define two groups of pa-
rameters which influence the formula of the compo-
nent fitness function: the parameters from the former
one are embedded in the component function formula
whereas the parameters from the latter one control
rather the output of the formula application. For ex-
ample, when we want to stretch the landscape over the
search space each of the solution coordinates is multi-
plied by the scaling factor. For a non–uniform stretch-
ing we need to use a vector of factors containing in-
dividual values for each of the coordinates. We call
this type of modification a horizontal scaling and this
represents the first type of component changes. The
example of the second type is a vertical scaling where
just the fitness value of a solution is multiplied by a
scaling factor. The first group of parameters controls
changes like horizontal translation, horizontalscaling,
and rotation. For simplicity they are called horizon-
tal changes in the further text. The second group of
changes (called respectively vertical changes) is rep-
resented by vertical scaling and vertical translation.
All of the changes can be obtained by dynamic mod-
ification of respective parameters during the process
of search.
4.2 Horizontal Change Parameters
In this case the coordinates of the solution x (a vec-
tor, i.e., a matrix of size n by 1) are modified before
the component function equation is applied. The new
coordinates are obtained with the following formula:
x
′
= M·(W·(x+ X)) (4)
where X is a translation vector,W isa diagonal matrix
of scaling coefficients for the coordinates, and M is an
orthogonal rotation matrix.
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
34

Table 1:
Syringa
components.
name formula domain
Peak (F
1
) f(x) =
1
1+
∑
n
j=1
x
2
j
[-100,100]
Cone (F
2
) f(x) = 1 −
q
∑
n
j=1
x
2
j
[-100,100]
Sphere (F
3
) f(x) =
∑
n
i=1
x
2
i
[-100,100]
Rastrigin (F
4
) f(x) =
∑
n
i=1
(x
2
i
−10cos(2πx
i
) + 10) [-5,5]
Griewank (F
5
) f(x) =
1
4000
∑
n
i=1
(x
i
)
2
−
∏
n
i=1
cos(
x
i
√
i
) + 1 [-100,100]
Ackley (F
6
) f(x) = −20exp(−0.2
r
1
n
n
∑
i=1
x
2
i
) −exp(
1
n
n
∑
i=1
cos(2πx
i
)) + 20+ e [-32,32]
4.3 Vertical Change Parameters
Changes of the fitness function value are executed ac-
cording to the following formula:
f
′
(x) = f(x) ·v+ h (5)
where v is a vertical scaling coefficient and h is a ver-
tical translation coefficient.
4.4 Parameters Control
In the case of dynamic optimization the fitness land-
scape components has to change the values of their
parameters during the process of search. There were
defined four different characteristics of variability
which were applied to the component parameters:
small step change (T
1
— eq. (6)), large step change
(T
2
— eq. (7)), and two versions of random changes
(T
3
— eq. (8) and T
4
— eq. (9)). The change ∆ of a
parameter value is calculated as follows:
∆ = α·r·(max−min); α = 0.04, r = U(0, 1), (6)
∆ = (α·sign(r
1
) + (α
max
−α) ·r
2
) ·(max−min);
α = 0.04, r
1,2
= U(0, 1), α
max
= 0.1 (7)
∆ = N(0,1) (8)
∆ = U(r
min
,r
max
) (9)
In the above-mentioned equations max and min rep-
resent upper and lower boundary of the search space,
N(0,1) is a random value obtained with gaussian dis-
tribution where µ = 0 and σ = 1, U(0, 1) is a ran-
dom value obtained with uniform distribution form
the range [0,1], and [r
min
,r
max
] define the feasible
range of ∆ values.
The model of
Syringa
assumes that the compo-
nent parameter control is separated from the compo-
nent, that is, a dynamic component has to consist of
two objects: the first one represents an evaluator of
solutions (i.e., a component of any type mentioned in
Table 1) and the second one is an agent which con-
trols the behavior of the evaluator. The agent defines
initial set of values for the evaluator parameters and
during the process of search the values are updated by
the agent according to the assumed characteristic of
variability. Properties of all the types of components
are unified so as to make possible assignment of any
agent to any component. This architecture allows to
create multiple classes of dynamic landscapes.
In the presented research we started with simu-
lation of two existing benchmarks: Generalized Dy-
namic Benchmark Generator (GDBG) (Li and Yang,
2008) and the Moving Peaks Benchmark genera-
tor (Branke, 1999). In both cases optimization is
carried out in a real-valued multidimensional search
space, and the fitness landscape is built of multiple
component functions controlled individually by their
parameters. For appropriate simulation of any of the
two benchmarks there are just two things to do: select
a set of the right components and build agents which
will control the components in the same manner like
in the original benchmarks.
4.5 Simulation of Moving Peaks
Benchmark (MPB)
In the case of MPB, three scenarios of the benchmark
parameters control are defined (Branke, 1999). We
did experiments for the first and the second scenario.
The selected fitness landscape consists of a set of
peaks (F
1
— the first scenario) or cones (F
2
— the sec-
ond scenario) which undergo two types of horizontal
changes: the translation and the scaling and just one
vertical change, that is, the translation. The horizon-
tal scaling operator has the same scale coefficient for
each of the dimensions, so in this specific case this co-
efficient is represented as a one-dimensional variable
w instead of the vector W.
The parameters X, w and v are embedded into the
HYBRID RULES OF PERTURBATION IN DIFFERENTIAL EVOLUTION FOR DYNAMIC OPTIMIZATION
35

peak function formula f(x) in the following way:
f
peak
(x) =
v
1+ w·
∑
n
j=1
(x
j
−X
j
)
2
n
(10)
The parameters X, w and h are embedded into the
cone function formula f(x) in the following way:
f
cone
(x) = h −w·
s
n
∑
j=1
(x
j
−X
j
)
2
(11)
All the modifications of the component parame-
ters belong to the fourth characteristic of variability
T
4
where for every change r
min
and r
max
are rede-
fined in the way to keep the value of each modified
parameter in the predefined interval of feasible val-
ues. Simply, for every modified parameter of transla-
tion or scaling, which can be represented as a symbol
p: r
min
= p
min
− p and r
max
= p
max
− p. For the hor-
izontal scaling the interval is set to [1;12] and for the
vertical scaling — to [30;70]. For the horizontal trans-
lation there is a constraint for the euclidean length of
the translation: |X|≤3. For both scenarios in the first
version there are ten moving components whereas in
the second version 50 moving components is in use.
4.6 Simulation of Generalized Dynamic
Benchmark Generator (GDBG)
GDBG consists of two different benchmarks:
Dynamic Rotation Peak Benchmark Generator
(DRPBG) and Dynamic Composition Benchmark
Generator (DCBG). There are five types of com-
ponent functions: peak (F
1
), sphere (F
3
), Rastrigin
(F
4
), Griewank (F
5
), and Ackley (F
6
). F
1
is the base
component for DRPBG whereas all the remaining
types are employed in DCBG.
4.6.1 Dynamic Rotation Peak Benchmark
Generator (DRPBG)
There are four types of the component parameter
modification applied in DRPBG: horizontal transla-
tion, scaling and rotation and vertical scaling. As in
the case of MPB the horizontal scaling operator has
the same scale coefficient for each of the dimensions,
so in this specific case this coefficient is also repre-
sented as a one-dimensional variable w instead of the
vector W. The component function formula is the
same as in the eq. (10).
Values of the translation vector X in subsequent
changes are evaluated with use of the rotation ma-
trix M. Clearly, we apply the rotation matrix to the
current coordinates of the component function opti-
mum o, that is: o(t + 1) = o(t) · M(t) (where t is
the number of the current change in the component)
and then the final value of X(t + 1) is calculated:
X(t + 1) = o(t + 1) −o(0).
Subsequent values of the horizontal scaling pa-
rameter w and the vertical scaling parameter v are
evaluated according to the first, the second or the third
characteristic of variability, that is, T
1
, T
2
or T
3
.
For every change a new rotation matrix M is gen-
erated which is common for all the components. The
rotation matrix M is obtained as a result of multipli-
cation of a number of rotation matrices R where each
of R represents rotation in just one plane of the multi-
dimensional search space.
In DRPBG we start with a selection of the rotation
planes, that is, we need to generate a vector r of size
l where l is an even number and l ≤ n/2. The vec-
tor contains randomly selected search space dimen-
sion identifiers without repetition. Then for each of
the planes defined in r by subsequent pairs of indices:
[1,2], [3,4], [5,6], .. . [l −1,l] their rotation angles are
randomly generated and finally respective matrices
R
r[1],r[2]
,... R
r[l− 1],r[l]
are calculated (R
ij
(θ) represents
rotation by the θ angle along the plane i–j) (c.f. (Sa-
lomon, 1996)). Eventually, the rotation matrix M is
calculated as follows:
M(t) = R
r[1],r[2]
(θ(t))···R
r[l− 1],r[l]
(θ(t)). (12)
In
Syringa
the method of the rotation matrix gen-
eration slightly differs from the one described above.
Instead of the vector r there is a vector Θ which repre-
sents a sequence of rotation angles for all the possible
planes in the search space. The position in the vector
Θ defines the rotation plane. Simply, Θ(1) represents
the plane [1,2], Θ(2) represents the plane [2,3] and
so on until the plane [n-1,n]. Then there go planes
created from every second dimensions, that is, [1,3],
[2,4] and so on until the plane [n-2,n]. Then there
go planes created from every third dimensions, then
those created from every fourth, and so on until there
appears the last plane created from the first and the
last dimension. When Θ(i) equals zero this means,
that there is no rotation for the i-th plane, otherwise
the respective rotation matrix R is generated. The fi-
nal stage of generation of the matrix M is the same
as in the description above, that is, the rotation matrix
M is the result of multiplication of all the matrices R
generated from the vector Θ.
Finally, it is important to note that in the above
description the matrix M has been used twice for the
evaluation of the component modification parameters:
the first time when the translation vector X is calcu-
lated and the second time when the rotation is applied,
that is, just before the application of the equation (10).
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
36

4.6.2 Dynamic Composition Benchmark
Generator (DCBG)
DCBG performs five types of the component param-
eter modification: horizontal translation, scaling and
rotation and vertical translation and scaling. The re-
spective parameters are embedded into the function
formula f”(x) in the following way (Liang et al.,
2005; Suganthan et al., 2005):
f”(x) = (v·( f
′
(M·(W·(x+ X))) + h)) (13)
where:
v is the weight coefficient depending of the
currently evaluated x,
W is called a stretch factor which equals 1
when the search range of f(x) is the same as
the entire search space and grows when the
search range of f(x) decreases,
f
′
(x) represent the value of f(x) normalized
in the following way: f
′
(x) = C · f(x)/|f
max
|
where the constant C = 2000 and f
max
is
the estimated maximum value of function f
which is one of the four: sphere (F
3
), Rastri-
gin (F
4
), Griewank (F
5
), or Ackley (F
6
).
In
Syringa
the properties of some of the parame-
ters has had to be changed. The first difference is in
the evaluation of the weight coefficient v which due to
the structure of the assumed model cannot depend of
the currently evaluated x. Therefore, we assumed that
v = 1. There is also no scaling, i.e., W is an identity
matrix because we assumed that the component func-
tions are always defined for the entire search space.
The last issue is about the rotation matrix M which is
calculated in the same way as for the
Syringa
version
of DRPBG. Eventually, the
Syringa
version of f”(x)
has the following shape:
f”(x) = (( f
′
(M·((x+ X))) + h)) (14)
Thus, the
Syringa
version of DCBG differs from
the original one because it does not contain the hor-
izontal scaling, the rotation matrix M is evaluated in
the different way and the stretch factor always equals
one. However, a kind of the vertical scaling is still
present and can be found in the step of the f (x) nor-
malization.
Fitness landscapes of the selected benchmark in-
stances generated for two-dimensional search space
are depicted in Figure 1. Please note that the land-
scape generated by DRPBG with ten peak compo-
nents is in fact exactly the same as the one which
would be generated by MPB sc.1 with ten peak com-
ponents since in both cases the same component func-
tion is in use. Of course the dynamics of the two
benchmark instances is different so there is no chance
for duplication of the experiments.
5 PLAN OF EXPERIMENTS
5.1 Performance Measure
For comparisons between the results obtained for dif-
ferent benchmark instances and different versions of
the algorithms the offline error (Branke, 1999)(briefly
oe) was selected. The measure represents the aver-
age deviation from the optimum of the best individual
value since the last change in the fitness landscape.
Formally:
oe =
1
N
changes
N
changes
∑
j=1
1
N
e
( j)
N
e
( j)
∑
i=1
( f(x
∗j
) − f(x
ji
best
))
!
,
(15)
where N
e
( j) is a total number of solution evaluations
performed for the j-th static state of the landscape,
f(x
∗j
) is the value of an optimal solution for the j-th
landscape and f(x
ji
best
) is the current best value found
for the j-th landscape. It should be clear that the mea-
sure oe should be minimized, that is, the better result
the smaller the value of oe.
Our algorithm has no embedded strategy for de-
tecting changes in the fitness landscapes. Simply,
the last step in the main loop of the algorithm exe-
cutes the reevaluation of the entire current solution
set. Therefore, our optimization system is informed
of the change as soon as it occurs, and no additional
computational effort for its detection is needed.
5.2 The Tests
We performed experiments with a subset of GDBG
benchmark functions as well as with four versions of
MPB. For each of the components there is a defined
feasible domain which, unfortunately, is not the same
in every case (see the last column in Table 1). For
this reason the boundaries for the search space dimen-
sions in the test-cases are not the same but adjusted re-
spectively to the components. For GDBG the feasible
search space is within the hypercube with the same
boundaries for each dimension, namely [−7.1,7.1]
whereas for MPB — [−50,50]. These box constraints
mean that both solutions and components should not
leave this area during the entire optimization process.
The number of fitness function evaluations be-
tween subsequent changes was calculated according
to the rules as in the CEC’09 competition, that is,
for 10
4
·n fitness function calls between subsequent
changes where n is a number of search space dimen-
sions and in this specific case n equals five for all of
the benchmark instances.
To decrease the number of algorithm configura-
tions which would be experimentally verified we de-
HYBRID RULES OF PERTURBATION IN DIFFERENTIAL EVOLUTION FOR DYNAMIC OPTIMIZATION
37

-4
-2
0
2
4
x
1
-4
-2
0
2
4
x
2
0
10
20
30
40
50
60
70
0
10
20
30
40
50
60
70
-4
-2
0
2
4
x
1
-4
-2
0
2
4
x
2
0
5000
10000
15000
20000
25000
30000
0
5000
10000
15000
20000
25000
30000
-4
-2
0
2
4
x
1
-4
-2
0
2
4
x
2
0
5000
10000
15000
20000
25000
30000
0
5000
10000
15000
20000
25000
30000
-4
-2
0
2
4
x
1
-4
-2
0
2
4
x
2
0
200
400
600
800
1000
1200
1400
1600
1800
0
200
400
600
800
1000
1200
1400
1600
1800
-4
-2
0
2
4
x
1
-4
-2
0
2
4
x
2
0
5000
10000
15000
20000
25000
0
5000
10000
15000
20000
25000
-40
-20
0
20
40
x
1
-40
-20
0
20
40
x
2
0
10
20
30
40
50
60
70
0
10
20
30
40
50
60
70
Figure 1: Fitness landscapes of the benchmark instances for 2D search space: DRPBG with ten peak components and DCBG
with ten sphere components (first row), DCBG with ten Rastrigin components and DCBG with ten Griewank components
(second row), DCBG with ten Ackley components and MPB sc. 2 with ten cones (the last row).
cided to fix the value of the parameter r
SαS
and the
only varied parameter was α. In the preliminary
phase of experimental research we tested efficiency
of the algorithm for different values of r
SαS
and ana-
lyzed obtained values of error. Eventually, for GDBG
r
SαS
= 0.6 whereas for MPB it is ten times smaller,
that is, r
SαS
= 0.06. Thus, for each of the benchmark
instances there were performed just 32 experiments:
for α between 0.25 and 2 varying with step 0.25 and
for 0, 1, 2 and 3 solutions of new type present in the
population. For each of the configurations the experi-
ments were repeated 20 times and each of them con-
sisted of 60 changes in the fitness landscape. Graphs
and tables present mean values of oe calculated for
these series.
6 THE RESULTS
The best values of offline error obtained for each of
the benchmarkinstances are presented in Table 2. The
table contains names of the instances, the mutation
parameter configurations (i.e. values of α and ind
SαS
)
and the mean values of oe. The instances are sorted in
ascending order of obtained oe values (more or less).
This way we can easily show which of the instances
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
38
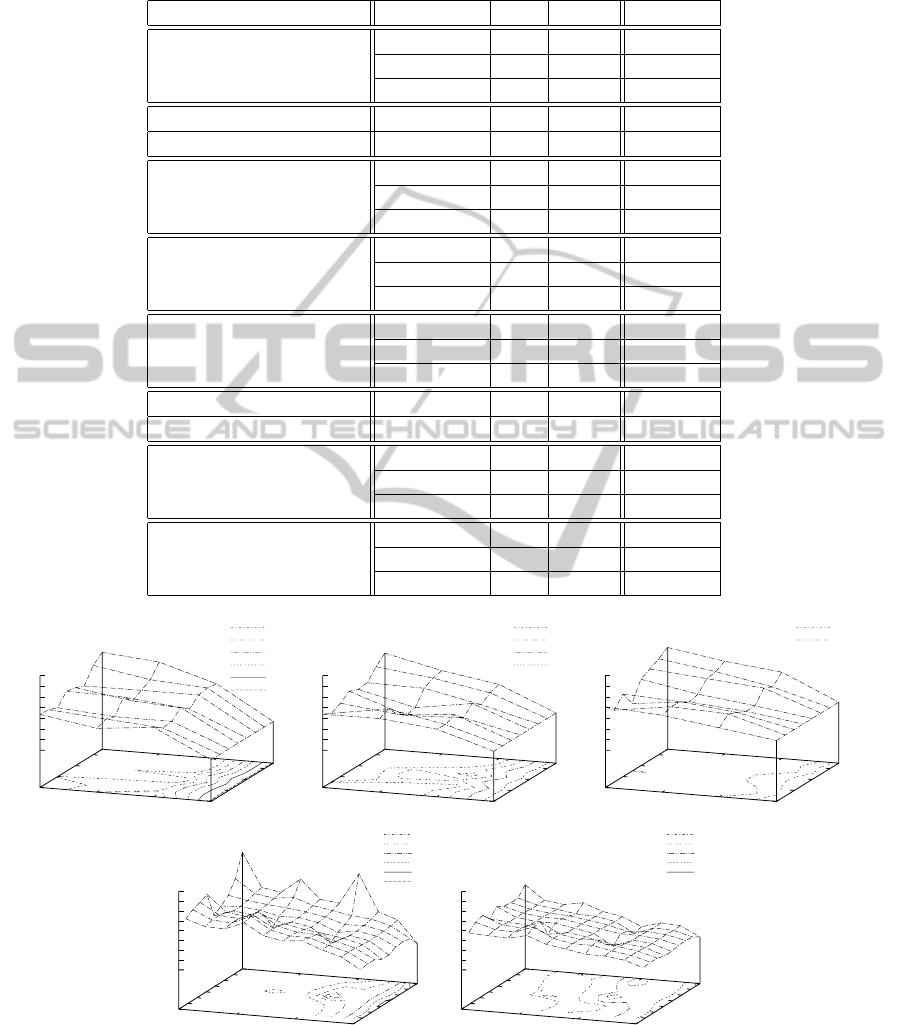
Table 2: The least offline error (oe) mean values obtained for all the benchmark instances; the instances are sorted in ascending
order of oe; for each of the instances three values are presented for three change types of the GDBG control parameters: T
1
,
T
2
and T
3
(except for MPB where there are two cases: with ten and 50 peaks/cones).
the benchmark instance change type α ind
SαS
oe
F
5
T
1
1.25 3.00 0.16813
(Griewank) T
2
1.50 3.00 0.13977
T
3
2.00 3.00 0.35606
MPB sc. 1 with ten peaks 1.00 1.00 0.35622
MPB sc. 1 with 50 peaks 1.50 1.00 0.66492
DCBG with F
3
T
1
1.50 2.00 1.22583
(sphere components) T
2
0.75 1.00 1.81625
T
3
1.75 3.00 5.32476
DRPBG with ten F
1
T
1
2.00 1.00 1.98783
T
2
1.00 1.00 2.51758
T
3
0.50 1.00 3.76098
DRPBG with 50 F
1
T
1
1.25 1.00 3.35855
T
2
1.00 1.00 4.24594
T
3
0.75 1.00 5.87459
MPB sc. 2 with ten cones — 0.00 4.11117
MPB sc. 2 with 50 cones 0.50 1.00 3.74856
DCBG with F
6
T
1
2.00 1.00 8.41941
(Ackley components) T
2
1.50 1.00 9.77345
T
3
1.50 1.00 14.24450
DCBG with F
4
T
1
— 0.00 570.72
(Rastrigin components) T
2
— 0.00 610.565
T
3
— 0.00 661.395
0
1
2
3
0.5
1
1.5
2
550
600
650
700
750
800
850
900
700
675
650
625
600
575
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
550
600
650
700
750
800
850
900
700
675
650
625
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
550
600
650
700
750
800
850
900
700
675
ind
S α S
α
0
1
2
3
0.25
0.5
0.75
1
1.25
1.5
1.75
2
4
5
6
7
8
9
10
11
12
7
6.5
6
5.5
5
4.5
ind
S α S
α
0
1
2
3
0.25
0.5
0.75
1
1.25
1.5
1.75
2
4
4.5
5
5.5
6
6.5
7
7.5
8
5.5
5.25
5
4.75
4.5
ind
S α S
α
Figure 2: Characteristics of oe for jDE: the cases where hybrid solution deteriorates the results, i.e., DCBG with F
4
(Rastrigin
components) (the first row) and MPB sc.2 with 10 and 50 F
2
(cones) (the second row); the subsequent graphs in the first row
represent three change types of the GDBG control parameters: T
1
, T
2
and T
3
.
were the most difficult and which were the easiest.
All the results are depicted in Figures 2 and 3. The
graphs are divided into two groups: where due to the
presence of s
Lev´y
solutions obtained results deterio-
HYBRID RULES OF PERTURBATION IN DIFFERENTIAL EVOLUTION FOR DYNAMIC OPTIMIZATION
39
0
1
2
3
0.5
1
1.5
2
0.1
0.12
0.14
0.16
0.18
0.2
0.22
0.24
0.26
0.28
0.3
0.2
0.18
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
0.1
0.12
0.14
0.16
0.18
0.2
0.22
0.24
0.26
0.28
0.3
0.2
0.18
0.16
0.14
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
0.3
0.4
0.5
0.6
0.7
0.8
0.5
0.45
0.4
ind
S α S
α
0
1
2
3
0.25
0.5
0.75
1
1.25
1.5
1.75
2
0.3
0.35
0.4
0.45
0.5
0.55
0.6
0.65
0.7
0.55
0.5
0.45
0.4
ind
S α S
α
0
1
2
3
0.25
0.5
0.75
1
1.25
1.5
1.75
2
0.5
0.6
0.7
0.8
0.9
1
1.1
0.8
0.75
0.7
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
1
1.5
2
2.5
3
3.5
4
2
1.75
1.5
1.25
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
1
1.5
2
2.5
3
3.5
4
2
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
5
5.5
6
6.5
7
7.5
8
8.5
9
6.5
6.25
6
5.75
5.5
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
2
3
4
5
6
7
8
5
4.5
4
3.5
3
2.5
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
2
3
4
5
6
7
8
5
4.5
4
3.5
3
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
3
4
5
6
7
8
9
7
6.5
6
5.5
5
4.5
4
3.5
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
3
4
5
6
7
8
9
10
6
5.5
5
4.5
4
3.5
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
3
4
5
6
7
8
9
10
6
5.5
5
4.5
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
5
6
7
8
9
10
11
12
13
8
7.5
7
6.5
6
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
8
10
12
14
16
18
20
22
14
13
12
11
10
9
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
8
10
12
14
16
18
20
22
14
13
12
11
10
ind
S α S
α
0
1
2
3
0.5
1
1.5
2
14
16
18
20
22
24
26
28
30
32
20
19
18
17
16
15
ind
S α S
α
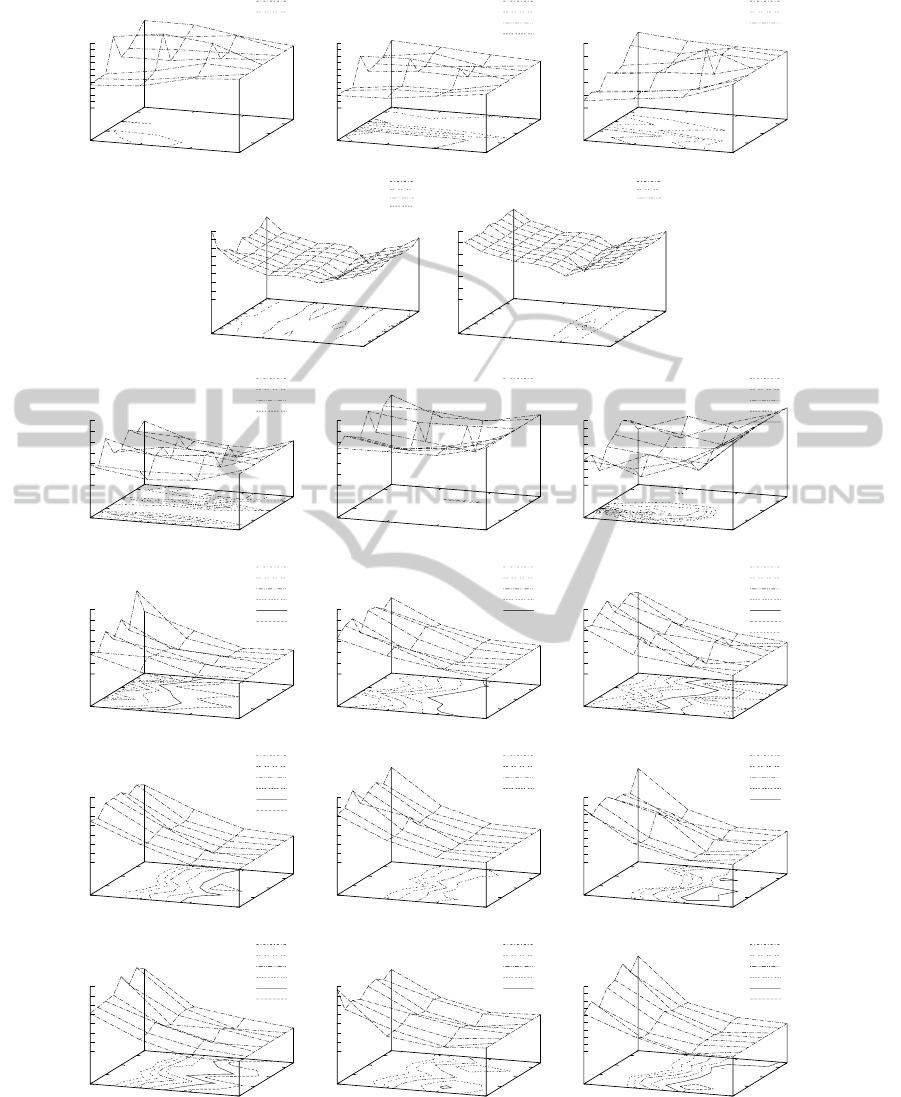
Figure 3: Characteristics of oe for jDE: the cases where hybrid solution improves the results: DCBG with F
5
(Griewank
components) (the first row), MPB sc.1 with ten and with 50 F
1
(peaks) (the second row) DCBG with F
2
(sphere components)
(the third row), DRPBG with ten and with 50 F
1
(peaks) (the fourth and the fifth row), DCBG with F
6
(Ackley components)
(the last row); the columns represent three change types of the GDBG control parameters: T
1
, T
2
and T
3
(except for MPB
where there are just two cases: with ten and 50 peaks).
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
40

rated (Figure 2), and where application of s
Lev´y
solu-
tions in the population improved the results, that is,
obtained error decreased (Figure 3).
For each of the benchmark instances there were
obtained 32 values of oe which are presented in a
graphicalform as a surface generated for different val-
ues of the number of s
Lev´y
solutions (that is, ind
SαS
)
and α. The benchmark instances in the Figures are
ordered in the same way as in Table 2.
7 CONCLUSIONS
In this paper we introduce hybrid structure of popula-
tion in differential evolution algorithm jDE and study
its properties when applied to dynamic optimization
tasks. This is a case of a kind of technology trans-
fer where promising mechanisms form one heuris-
tic approach appear to be useful in another. The re-
sults show that mutation operator using random vari-
ates based on α-stable distribution, that is, the oper-
ator where both fine local modification and macro-
jumps can appear, improves the values of oe. Lack
of improvement appeared in two cases, that is, for
the DCBG with F4 (Rastrigin components) which is a
very difficult landscape looking like a hedgehog (Fig-
ure 1, the graph in the second row on the left) and for
the MPB sc.2 with ten cones. In both cases macro-
mutation most probably introduces unnecessary noise
rather than a chance for exploration of a new promis-
ing area. Difficulty of the former benchmark instance
is confirmed by extremely high values of error ob-
tained for all three types of change.
In the remaining cases the influence of s
Lev´y
solu-
tion presence is positive, however, it must be stressed
that the number of these solutions should be small. In
most cases the best results were obtained for just one
piece. The exception is the DCBG with F5 (Grievank
components) which was the easiest landscape for the
algorithm, easier even than the landscape build of the
spheres. In the case of the DCBG with F5 the higher
number of s
Lev´y
, the smaller value of oe.
Finally, it is worth to stress that the different com-
plexity of the tested instances shows also that when
we take them as a suite of tests and evaluate over-
all gain of the algorithm we need to apply different
weight for the successes obtained for each of the in-
stances. Simply, an improvement of efficiency ob-
tained for DCBG with Grievank components havedif-
ferent significance than the same improvement for,
e.g., DCBG with Ackley components.
REFERENCES
Branke, J. (1999). Memory enhanced evolutionary algo-
rithm for changing optimization problems. In Proc. of
the Congr. on Evolutionary Computation, volume 3,
pages 1875–1882. IEEE Press, Piscataway, NJ.
Brest, J., Greiner, S., Boskovic, B., Mernik, M., and Zumer,
V. (2006). Self-adapting control parameters in dif-
ferential evolution: A comparative study on numeri-
cal benchmark problems. IEEE Trans. Evol. Comput.,
10(6):646–657.
Brest, J., Zamuda, A., Boskovic, B., Maucec, M. S., and
Zumer, V. (2009). Dynamic optimization using self-
adaptive differential evolution. In IEEE Congr. on
Evolutionary Computation, pages 415–422. IEEE.
Feokistov, V. (2006). Differential Evolution, In Search of
Solutions, volume 5 of Optimization and Its Applica-
tions. Springer.
Li, C. and Yang, S. (2008). A generalized approach to con-
struct benchmark problems for dynamic optimization.
In Simulated Evolution and Learning, SEAL, volume
5361 of LNCS, pages 391–400. Springer.
Liang, J. J., Suganthan, P. N., and Deb, K. (2005). Novel
composition test functions for numerical global opti-
mization. In IEEE Swarm Intelligence Symposium,
pages 68–75, Pasadena, CA, USA.
Price, K. V. (1994). Genetic annealing. Dr. Dobb’s Journal,
pages 127–132.
Price, K. V., Storn, R. M., and Lampinen, J. A. (2005). Dif-
ferential Evolution, A Practical Approach to Global
Optimization. Natural Computing Series. Springer.
Salomon, R. (1996). Reevaluating genetic algorithm perfor-
mance under coordinate rotation of benchmark func-
tions. BioSystems, 39(3):263–278.
Suganthan, P. N., Hansen, N., Liang, J. J., Deb, K., Chen,
Y.-P., Auger, A., and Tiwari, S. (2005). Problem defi-
nitions and evaluation criteria for the cec 2005 special
session on real-parameter optimization. Technical re-
port, Nanyang Technological University, Singapore.
Trojanowski, K. (2009). Properties of quantum particles in
multi-swarms for dynamic optimization. Fundamenta
Informaticae, 95(2-3):349–380.
HYBRID RULES OF PERTURBATION IN DIFFERENTIAL EVOLUTION FOR DYNAMIC OPTIMIZATION
41
