
GLOBAL COMPETITIVE RANKING FOR CONSTRAINTS
HANDLING WITH MODIFIED DIFFERENTIAL EVOLUTION
Abul Kalam Azad and Edite M. G. P. Fernandes
Algoritmi R&D Center, School of Engineering, University of Minho, 4710-057 Braga, Portugal
Keywords:
Constrained nonlinear programming, Constraints handling, Ranking, Differential evolution.
Abstract:
Constrained nonlinear programming problems involving a nonlinear objective function with inequality and/or
equality constraints introduce the possibility of multiple local optima. The task of global optimization is to
find a solution where the objective function obtains its most extreme value while satisfying the constraints.
Depending on the nature of the involved functions many solution methods have been proposed. Most of the
existing population-based stochastic methods try to make the solution feasible by using a penalty function
method. However, to find the appropriate penalty parameter is not an easy task. Population-based differential
evolution is shown to be very efficient to solve global optimization problems with simple bounds. To handle
the constraints effectively, in this paper, we propose a modified constrained differential evolution that uses
self-adaptive control parameters, a mixed modified mutation, the inversion operation, a modified selection and
the elitism in order to progress efficiently towards a global solution. In the modified selection, we propose a
fitness function based on the global competitive ranking technique for handling the constraints. We test 13
benchmark problems. We also compare the results with the results found in literature. It is shown that our
method is rather effective when solving constrained problems.
1 INTRODUCTION
Problems involving global optimization over contin-
uous spaces are ubiquitous throughout the scientific
community. Many real world problems are formu-
lated as mathematical programming problems involv-
ing continuous variables with linear/nonlinear objec-
tive function and constraints. The constraints can be
of inequality and equality type. Generally, the con-
strained nonlinear programming problems are formu-
lated as follows:
minimize f(x)
subject to g
k
(x) ≤ 0 k = 1, 2,. . ., m
1
h
l
(x) = 0 l = 1, 2, . . . , m
2
l
j
≤ x
j
≤ u
j
j = 1, 2, . . . , n,
(1)
where, f, g
k
, h
l
: R
n
−→ R with feasible set F = {x ∈
R
n
: g(x) ≤ 0, h(x) = 0 and l ≤ x ≤ u}. f, g
k
, h
l
may
be differentiable and the information about deriva-
tives may or may not be provided.
Problem (1) involving global optimization (here
we consider a minimization problem) of a multivari-
ate function with constraints is widespread in the
mathematical modeling of real world systems. Many
problems can be described only by nonlinear relation-
ships, which introduce the possibility of multiple lo-
cal minima. The task of the global optimization is to
find a solution where the objectivefunction obtains its
most extreme value, the global minimum, while satis-
fying the constraints.
In the last decades, manystochastic solution meth-
ods with different constraints handling techniques
have been proposed to solve (1). Stochastic meth-
ods involve a random sample of solutions and the
subsequent manipulation of the sample to find good
local (and hopefully global) minima. The stochas-
tic methods can be based on a point-to-point search
or on a population-based search. Most of the exist-
ing population-based stochastic methods try to make
the solution feasible by repairing the infeasible one
or penalizing an infeasible solution with a penalty
function method. However, to find the appropriate
penalty parameter is not an easy task. (Deb, 2000)
proposed an efficient constraints handling technique
for genetic algorithms based on the feasibility and
dominance rules. The author used a penalty function
that does not require any penalty parameter. (Bar-
bosa and Lemonge, 2003) proposed a parameter-less
adaptive penalty scheme for genetic algorithms ap-
plied to constrained optimization problems. In the
42
Kalam Azad A. and M. G. P. Fernandes E..
GLOBAL COMPETITIVE RANKING FOR CONSTRAINTS HANDLING WITH MODIFIED DIFFERENTIAL EVOLUTION.
DOI: 10.5220/0003672200420051
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 42-51
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

very recent paper the authors proposed this adap-
tive penalty scheme for differential evolution (Silva
et al., 2011). (Hedar and Fukushima, 2006) proposed
a filter simulated annealing method for constrained
continuous global optimization problems. The au-
thors used the filter method (Fletcher and Leyffer,
2002) rather than the penalty method to handle the
constraints. Runarsson and Yao proposed a stochas-
tic ranking (Runarsson and Yao, 2000) and a global
competitive ranking (Runarsson and Yao, 2003) tech-
nique for constrained evolutionary optimization based
on evolution strategy. The authors presented a new
view on the usual penalty function methods in terms
of the dominance of penalty and objective func-
tions. (Dong et al., 2005) proposed a swarm op-
timization based on constraint fitness priority-based
ranking technique. (Zahara and Hu, 2008) proposed
constrained optimization with a hybrid Nelder-Mead
simplex method and a particle swarm optimization.
The authors also used constraint fitness priority-based
ranking technique for constraints handling. Rocha
and Fernandes proposed the feasibility and domi-
nance rules (Rocha and Fernandes, 2008) and the self-
adaptive penalties (Rocha and Fernandes, 2009) in
the electromagnetism-like algorithm for constrained
global optimization problems. (Coello, 2000) pro-
posed constraints handling using an evolutionary mul-
tiobjective optimization technique. This author intro-
duced the concept of nondominance (commonly used
in multiobjective optimization) as a way to incorpo-
rate constraints into the fitness function of a genetic
algorithm. (Coello and Cort´es, 2004) proposed hy-
bridizing a genetic algorithm with an artificial im-
mune system for global optimization. The authors
used genotypic-based distances to move from infeasi-
ble solution to feasible one. Another constraints han-
dling technique is the multilevel Pareto ranking based
on the constraints matrix (Ray and Tai, 2001; Ray and
Liew, 2003). This technique is based on the concepts
of Pareto nondominance in multiobjective optimiza-
tion. (Ray and Tai, 2001) proposed an evolutionary
algorithm with a multilevel pairing strategy and (Ray
and Liew, 2003) proposed a society and civilization
algorithm based on the simulation of social behaviour.
Differential evolution (DE) proposed by (Storn
and Price, 1997) is a population-based heuristic ap-
proach that is very efficient to solve global opti-
mization problems with simple bounds. DE’s per-
formance depends on the amplification factor of dif-
ferential variation and crossover control parameter.
Hence self-adaptive control parameters have been im-
plemented in DE in order to obtain a competitive al-
gorithm. Further, to improve solution accuracy, tech-
niques that are able to exploit locally certain regions,
detected in the search space of the problem as promis-
ing, are also required. A local search starts from
a candidate solution and then iteratively moves to a
neighbour solution. Typically, every candidate solu-
tion has more than one neighbour solutions and the
choice of movement depends only on the information
about the solutions in the neighbourhood of the cur-
rent one. When the solutions ought to be restricted
to a set of equality and inequality constraints, an ef-
ficient constraints handling technique is also required
in the solution method. In this paper, we propose a
modified constrained differential evolution algorithm
(herein denoted as m-CDE) that uses self-adaptive
control parameters (Brest et al., 2006), a mixture of
modified mutations (Kaelo and Ali, 2006), and also
includes the inversion operation, a modified selection
and the elitism to be able to progress efficiently to-
wards a global solution of problems (1). To handle
the constraints effectively, the modified selection in-
corporates the global competitive ranking technique
to assess the fitness of all individual points in the pop-
ulation.
The organization of this paper is as follows. We
describe the constraints handling techniques in Sec-
tion 2. In Section 3 the modified constrained differ-
ential evolution is outlined. Section 4 describes the
experimental results and finally we draw the conclu-
sions of this study in Section 5.
2 CONSTRAINTS HANDLING
TECHNIQUES
Stochastic methods are mostly developed for the
global optimization of unconstrained problems. Fi-
nally, they are extended to the constrained problems
with the modification of solution procedures or by
applying penalty function methods. In population-
based techniques, the widely used approach to deal
with constrained optimization problems is based on
penalty functions. In penalty functions, a penalty term
is added to the objective function in order to penalize
the constraint violation. This enable us to transform
a constrained optimization problem into a sequence
of unconstrained subproblems, whose objective func-
tion is
ψ(x) = f(x) + µH[ζ(x)], (2)
where ζ(x) is a real-valued function and is greater
than or equal to 0 aiming at measuring the constraint
violation, H is a function of the constraint violation,
and µ defines a positive penalty parameter aiming at
balancing objective and constraint violation. An indi-
vidual point is feasible if ζ(x) = 0.
GLOBAL COMPETITIVE RANKING FOR CONSTRAINTS HANDLING WITH MODIFIED DIFFERENTIAL
EVOLUTION
43

In constrained optimization, it is very important
to find the right balance between the objective func-
tion and the constraint violation. The penalty func-
tion method can be applied to any type of constraints,
but the performance of penalty-type methods is not
always satisfactory. Usually, µ is updated throughout
the iterative process, so that the sequence of the solu-
tions of the unconstrained subproblems converges to
the solution of the constrained problem. Small values
of µ can produce almost optimal but infeasible solu-
tions. On the other hand, large values of µ can give
feasible solutions although an optimal solution in the
boundary may not be found. Hence, the most diffi-
cult aspect of a penalty function method is to deter-
mine the appropriate value to initialize the parameter
µ, as well as the rule for its updating. For this rea-
son alternative constraints handling techniques have
been proposed in the last decades. Here, three differ-
ent constraints handling techniques, usually used in
population-based methods - stochastic ranking, global
competitive ranking, and the feasibility and domi-
nance rules - have been implemented, and extensively
tested, in our m-CDE algorithm. They are briefly de-
scribed below.
2.1 Stochastic Ranking
(Runarsson and Yao, 2000) first proposed stochastic
ranking for the constrained optimization. This is a
bubble-sort-like algorithm to give ranks to individ-
uals in a population stochastically. In this ranking
method, two adjacent individual points are compared
and given ranks and swapped. The algorithm is halt
if there is no swap. Individuals are ranked primar-
ily based on their constraint violations. The objective
function values are then considered if: i) individu-
als are feasible, or ii) a uniform random number be-
tween 0 and 1 is less than or equal to P
f
. The proba-
bility P
f
is used only for comparisons of the objective
function in the infeasible region of the search space.
That is, given any pair of two adjacent individual
points, the probability of comparing them (in order to
determine which one is fitter) according to the objec-
tive function is 1 if both individuals are feasible; oth-
erwise it is P
f
. Such ranking ensures that good feasi-
ble solutions as well as promising infeasible ones are
ranked in the top of the population.
In our implementation of the stochastic ranking
(SR) method (Runarsson and Yao, 2000) in the modi-
fied constrained differential evolution, each individual
point x
i
is evaluated according to the fitness function
Φ
SR
(x
i
) =
I
i
− 1
N − 1
, (3)
where I
i
represents the rank of the point x
i
of the pop-
ulation and N is the number of individuals in a pop-
ulation. From (3), the fitness of an individual point
having the highest rank will be 0 and that with the
lowest rank will be 1. The best individual point in a
population has the lowest fitness value.
2.2 Global Competitive Ranking
(Runarsson and Yao, 2003) proposed another con-
straints handling technique for constrained problems
in order to strike the right balance between the ob-
jective function and the constraint violation. This
method is called global competitive ranking. In this
method, an individual point is ranked by comparing it
against all other members of the population.
In this ranking process, after calculating f and ζ
for all the individuals, f and ζ are sorted separately
in ascending order (since we consider the minimiza-
tion problem) and given ranks. Special considera-
tion is given to the tied individuals. In the case of
tied individuals the same higher rank will be given.
For example, in these eight individuals, already in as-
cending order, h6, (5, 8), 1, (2, 4, 7), 3i (individuals in
parentheses havesame value) the correspondingranks
are I(6) = 1, I(5) = I(8) = 2, I(1) = 4, I(2) = I(4) =
I(7) = 5, I(3) = 8. After the ranking of all the in-
dividuals based on the objective function f and the
constraint violation ζ, separately, the fitness function
of each individual point x
i
is given by
Φ
GR
(x
i
) = P
f
I
i, f
− 1
N − 1
+ (1− P
f
)
I
i,ζ
− 1
N − 1
, (4)
where Φ
GR
means fitness based on the global com-
petitive ranking (GR), and I
i, f
and I
i,ζ
are the ranks of
point x
i
based on the objective function and the con-
straint violation, respectively. P
f
indicates the prob-
ability that the fitness is calculated based on the rank
of objective function. It is clear from the above that
P
f
can be used easily to bias the calculation of fitness
accordingto the objectivefunction or the average con-
straint violation. The probability should take a value
0.0 < P
f
< 0.5 in order to guarantee that a feasible
solution may be found. From (4), the fitness of an in-
dividual point is a value between 0 and 1, and the best
individual point in a population has the lowest fitness
value.
2.3 Feasibility and Dominance Rules
(Deb, 2000) proposed another constraints handling
technique for population-based solution methods. It
is based on a set of rules that use feasibility and domi-
nance (FD) principles, as follows. First, the constraint
violation ζ is calculated for all the individuals in a
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
44

population. Then the objective function f is evalu-
ated only for feasible individuals. Two individuals are
compared at a time, and the following criteria are al-
ways enforced:
1. any feasible point is preferred to any infeasible
point;
2. between two feasible points, one having better ob-
jective function is preferred;
3. between two infeasible points, one having smaller
constraint violation is preferred.
In this case, the fitness of each individual point x
i
is
calculated as follows
Φ
FD
(x
i
) =
f(x
i
) if x
i
is feasible
f
max, f
+ ζ(x
i
) otherwise,
(5)
where f
max, f
is the objective function of the worst fea-
sible solution in the population. When all individuals
are infeasible then its value is set to zero. This fitness
function is used to choose the best individual point in
a population.
3 MODIFIED CONSTRAINED
DIFFERENTIAL EVOLUTION
The population-based differential evolution algorithm
has become popular and has been used in many prac-
tical cases, mainly because it has demonstrated good
convergence properties and is easy to understand. DE
is a floating point encoding that creates a new candi-
date point by adding the weighted difference between
two individuals to a third one in the population. This
operation is called mutation. The mutant point’s com-
ponents are then mixed with the components of target
point to yield the trial point. This mixing of com-
ponents is referred to as crossover. In selection, a
trial point replaces a target point for the next genera-
tion only if it is considered an equal or better point.
In unconstrained optimization, the selection opera-
tion relies on the objective function. DE has three
parameters: amplification factor of differential varia-
tion F, crossover control parameter Cr, and popula-
tion size N.
It is not an easy task to set the appropriate param-
eters since these depend on the nature and size of the
optimization problems. Hence, self-adaptive control
parameters ought to be implemented. (Brest et al.,
2006) proposed self-adaptive control parameters for
DE when solving global optimization problems with
simple bounds. In most original DE, three points are
chosen randomly for mutation and the base point is
then chosen at random within the three. This has an
exploratory effect but it slows down the convergence
of DE. (Kaelo and Ali, 2006) proposed a modified
mutation for differential evolution.
The herein presented modified constrained differ-
ential evolution algorithm - m-CDE - for constrained
nonlinear programming problems (1) includes:
1. the self-adaptive control parameters F and Cr, as
proposed by (Brest et al., 2006);
2. a modified mutation that mixes the modification
proposed by (Kaelo and Ali, 2006) with the cycli-
cal use of the overall best point as base point;
3. the inversion operation;
4. a modified selection that is based on the fitness of
individuals;
5. the elitism.
The modification in mutation allows m-CDE to en-
hance the local search around the overall best point.
In modified selection of m-CDE, we introduce and
test the three different techniques described so far for
calculating the fitness function of individuals that are
capable to handle the constrained problems (1). The
modified constrained differential evolution is outlined
below.
The target point of m-CDE, at iteration/generation
z, is defined by x
i,z
= (x
i1,z
, x
i2,z
, . . . , x
in,z
), where n
is the number of variables of the optimization prob-
lem and i = 1, 2, . . . , N. N does not change during the
optimization process. The initial population is cho-
sen randomly and should cover the entire component
spaces.
Self-adaptive Control Parameters. In m-CDE, we
use self-adaptive control parameters for F andCr pro-
posed by (Brest et al., 2006) by generating a different
set (F
i
,Cr
i
) for each point x
i
in the population. The
new control parameters for next generation F
i,z+1
and
Cr
i,z+1
are calculated by
F
i,z+1
=
F
l
+ λ
1
× F
u
if λ
2
< τ
1
F
i,z
otherwise
Cr
i,z+1
=
λ
3
if λ
4
< τ
2
Cr
i,z
otherwise,
(6)
where λ
k
∼ U[0, 1], k = 1, . . . , 4 and τ
1
= τ
2
= 0.1 rep-
resent the probabilities to adjust parameters F
i
and
Cr
i
, respectively. F
l
= 0.1 and F
u
= 0.9, so the new
F
i,z+1
takes a value from [0.1, 1.0] in a random man-
ner. The new Cr
i,z+1
takes a value from [0, 1]. F
i,z+1
and Cr
i,z+1
are obtained before the mutation is per-
formed. So, they influence the mutation, crossover
and selection operations of the new point x
i,z+1
.
Modified Mutation. In m-CDE, this is a mixture of
two different types of mutation operations. We use
the mutation proposed in (Kaelo and Ali, 2006). After
choosing three points randomly, the best point among
GLOBAL COMPETITIVE RANKING FOR CONSTRAINTS HANDLING WITH MODIFIED DIFFERENTIAL
EVOLUTION
45

three based on the fitness function is selected for the
base point and the remaining two points are used as
differential variation, i.e., for each target point x
i,z
, a
mutant point is created according to
v
i,z+1
= x
r
3
,z
+ F
i,z+1
(x
r
1
,z
− x
r
2
,z
), (7)
where r
1
, r
2
, r
3
are randomly chosen from the set
{1, 2, . . . , N}, mutually different and different from
the running index i and r
3
is the index with the best fit-
ness (among the three points). This modification has
a local effect when the points of the population form
a cluster around the global minimizer.
Furthermore, at every B generations, the best point
found so far is used as the base point and two ran-
domly chosen points are used as differential variation,
i.e.,
v
i,z+1
= x
best
+ F
i,z+1
(x
r
1
,z
− x
r
2
,z
). (8)
These mixed modifications allow m-CDE to maintain
its exploratory feature and at the same time to exploit
the region around the best individual of the population
expediting the convergence.
Crossover. In order to increase the diversity of the
mutant points’ components, crossover is introduced.
To this end, the crossover point u
i,z+1
is formed,
where
u
ij,z+1
=
v
ij,z+1
if (r
j
≤ Cr
i,z+1
) or j = s
i
x
ij,z
if (r
j
> Cr
i,z+1
) and j 6= s
i
.
(9)
In (9), r
j
∼ U[0, 1] performs the mixing of jth com-
ponent of points, s
i
is randomly chosen from the set
{1, 2, . . . , n} and ensures that u
i,z+1
gets at least one
component from v
i,z+1
.
Inversion. Since in m-CDE, a point has n-
dimensional real components, inversion (Holland,
1975) can easily be applicable. With the inversion
probability (p
inv
∈ [0, 1]), two positions are chosen on
the point u
i
, the point is cut at those positions, and
the cut segment is reversed and reinserted back into
the point to create the trial point u
′
i
. In practice, m-
CDE with the inversion has been shown to give better
results than those obtained without the inversion. An
illustrative example of inversion is shown in Figure 1.
Bounds Check. When generating the mutant point
and when the inversion operation is performed, some
components can be generated outside the bound con-
straints. So, in m-CDE after inversion the bounds of
each component should be checked with the follow-
ing projection of bounds:
u
′
ij,z+1
=
l
j
if u
′
ij,z+1
< l
j
u
j
if u
′
ij,z+1
> u
j
u
′
ij,z+1
otherwise.
(10)
Modified Selection. In original DE, the target and the
trial points are compared based on their correspond-
ing objective function to decide which point becomes
a member of the next generation, that is if the trial
point’s objective function is less than or equal to the
that of target point, then the trial point will be the tar-
get point for the next generation.
In this paper, for constrained nonlinear program-
ming problems, we propose a modified selection
based on one of the fitness functions of individuals
discussed so far. When using the global competitive
ranking technique, all the target points at generation
z and trial points at generation z + 1 are ranked to-
gether and their corresponding fitness Φ
GR
are calcu-
lated. Then the modified selection is performed, i.e.,
the trial and the target points are compared to decide
which will be the new target points for next genera-
tion based on their calculated fitness by the following
way
x
i,z+1
=
u
′
i,z+1
if Φ
GR
(u
′
i,z+1
) ≤ Φ
GR
(x
i,z
)
x
i,z
otherwise.
(11)
After performing selection in m-CDE, the best point
is chosen in the current generation based on the lowest
fitness function of the target points.
A similar procedure is performed when the
stochastic ranking technique is implemented.
On the other hand, when using the feasibility and
dominance principles, the trial and the target points
are compared based on the three feasibility and dom-
inance rules to decide which will be the new target
points for next generation. After performing selec-
tion, the fitness function Φ
FD
for all the target points
are calculated, and the best point based on the lowest
fitness function in the current generation is chosen.
We remark that this point is the overall best point in
the entire generations so far.
Elitism. The elitism is also performed to keep the
best point found so far in the entire generations. The
elitism aims at preserving in the entire generations the
individual point that, with the constraint violation 0
or smaller than others, has the smaller objective func-
tion. This is only required when either the stochas-
tic ranking or the global competitive ranking is used
to calculate fitness of individuals. We remark that in
these two techniques, fitness values of individuals are
calculated at every generation based on their corre-
sponding ranks. Thus, the fitness of best individual
point (based on the objective function and the con-
straint violation) may not be the lowest one.
Termination Criterion. Let G
max
be the maximum
number of generations. If f
max,z
and f
min,z
are the
objective function values of the points that have the
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
46
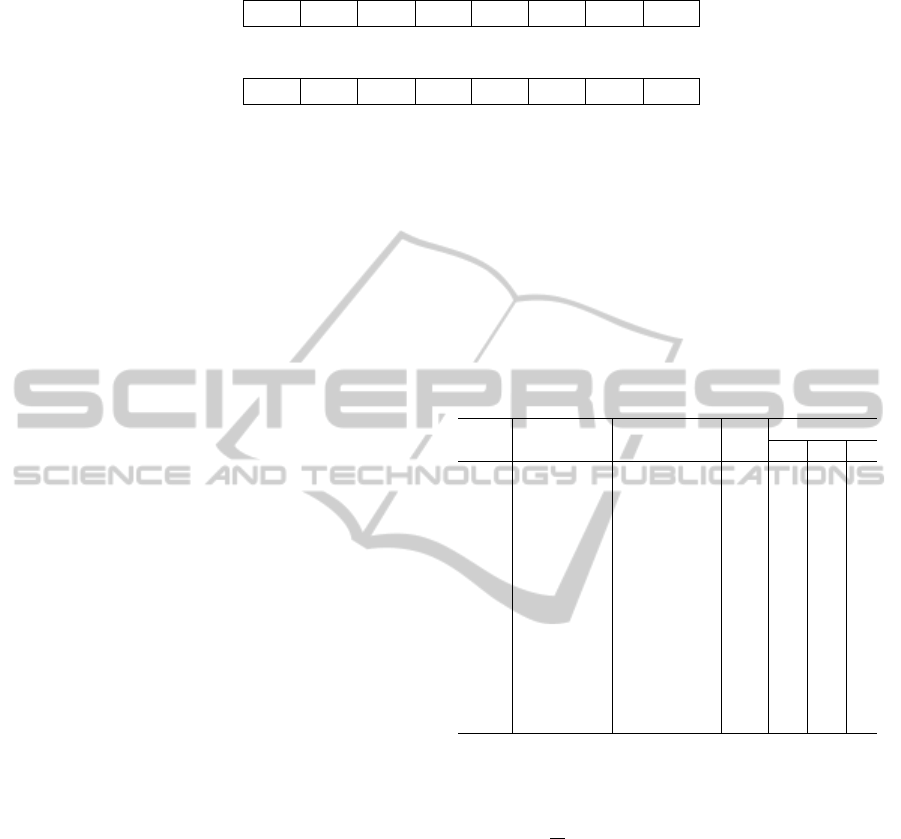
| |
u
i,z+1
=
u
i1,z+1
u
i2,z+1
u
i3,z+1
u
i4,z+1
u
i5,z+1
u
i6,z+1
u
i7,z+1
u
i8,z+1
⇓
| |
u
′
i,z+1
=
u
i1,z+1
u
i2,z+1
u
i6,z+1
u
i5,z+1
u
i4,z+1
u
i3,z+1
u
i7,z+1
u
i8,z+1
Figure 1: Inversion used in m-CDE.
highest and the lowest fitness function values respec-
tively, attained at generation z, then our m-CDE algo-
rithm terminates if (z > G
max
or ( f
max,z
− f
min,z
) ≤ η),
for a small positive number η.
3.1 The m-CDE Algorithm
The algorithm of the herein proposed modified con-
strained differential evolution for constrained global
optimization is described in the following:
Step 1. Set the values of parameters N, G
max
, B, P
f
,
F
l
, F
u
, τ
1
, τ
2
, p
inv
, and η.
Step 2. Set z = 1. Initialize the population x
1
, F
1
and
Cr
1
.
Step 3. Calculate the fitness function Φ(x
z
).
Step 4. Choose f
max,z
and f
min,z
from target points.
For stochastic and global competitive ranking,
perform the elitism to choose f
best
and x
best
.
Otherwise for feasibility and dominance rules
technique, set f
best
= f
min,z
and x
best
= x
min,z
.
Step 5. If the termination criterion is met stop. Oth-
erwise set z = z+ 1.
Step 6. Compute the control parameters F
z
and Cr
z
.
Step 7. Compute the mutant point v
z
:
If MOD(z, B) = 0; use (8). Otherwise use (7).
Step 8. Perform the crossover to make point u
z
.
Step 9. If a random number γ ∼ U[0, 1] ≤ p
inv
, per-
form inversion to make trial point u
′
z
.
Step 10. Check the bounds of the trial points.
Step 11. Calculate the fitness function Φ(x
z
) for all
the target and trial points.
Step 12. Perform the modified selection discussed
above.
Step 13. Go to step 4.
4 EXPERIMENTAL RESULTS
We code m-CDE in C with AMPL (Fourer et al.,
1993) interfacing and compile with Microsoft Visual
Studio 9.0 compiler in a PC having 2.5 GHz In-
tel Core 2 Duo processor and 4 GB RAM. We set
the value of parameters N = min(100, 10n), B = 10,
P
f
= 0.45, p
inv
= 0.05 and η = 10
−6
. We con-
sider 13 benchmark constrained nonlinear program-
ming problems (Runarsson and Yao, 2000). The char-
acteristics of these test problems are outlined in Ta-
ble 1. We model these problems in AMPL mod-
eling systems. To access these models please visit
http://www.norg.uminho.pt/emgpf/problems.htm.
Table 1: Characteristics of the test problems.
Prob.
Type of
f
opt
Var. Constraints
f n m
1
m
2
m
g01 quadratic -15.0000 13 9 0 9
g02 general -0.8036 20 2 0 2
g03 polynomial -1.0005 10 0 1 1
g04 quadratic -30665.5387 5 6 0 6
g05 cubic 5126.4967 4 2 3 5
g06 cubic -6961.8139 2 2 0 2
g07 quadratic 24.3062 10 8 0 8
g08 general -0.0958 2 2 0 2
g09 general 680.6301 7 4 0 4
g10 linear 7049.2480 8 6 0 6
g11 quadratic 0.7499 2 0 1 1
g12 quadratic -1.0000 3 1 0 1
g13 general 0.0539 5 0 3 3
The following average measure of constraint vio-
lation of an individual point x is used:
ζ(x) =
1
m
m
1
∑
k=1
max{0, g
k
(x)} +
m
2
∑
l=1
|h
l
(x)|
!
,
where m = m
1
+ m
2
is the total number of constraints.
In this paper, we consider an individual point as a fea-
sible one if ζ(x) ≤ δ, where δ is a very small positive
number. Here we set δ = 10
−8
.
We test m-CDE with the previously described
constraints handling techniques and compare their
performance using performance profiles (Dolan and
Mor´e, 2002). A comparison with other solution meth-
ods found in literature is also included.
4.1 Performance Profiles
For a fair comparison we run all the variants of m-
CDE in comparison for 30 times and reported the re-
sults. We used different G
max
for the 13 problems,
GLOBAL COMPETITIVE RANKING FOR CONSTRAINTS HANDLING WITH MODIFIED DIFFERENTIAL
EVOLUTION
47

but used the same value for all the variants. We
used the performance profiles proposed by (Dolan
and Mor´e, 2002) to evaluate and compare the per-
formance of the variants. Performance profiles are
the graphical representation of performance of differ-
ent solvers/variants/codes for a set of test problems
on the basis of their performance ratio. The perfor-
mance profile plot represents the cumulative distribu-
tion function of the performance ratio based on an ap-
propriate performance metric. The authors proposed
the computing time required to solve a problem as a
performance metric for different solvers (Dolan and
Mor´e, 2002), but other performance metrics could be
used.
In our comparative study, let P be the set of all
problems and S be the set of all variants of m-CDE.
Also let m
(p,s)
be the performance metric found by
variant s ∈ S on problem p ∈ P that measures the rel-
ative improvement of the objective function values, a
scaled distance to the optimal objectivefunction value
f
opt
(Ali et al., 2005), defined by
m
(p,s)
=
f
(p,s)
− f
opt
f
w
− f
opt
. (12)
In (12), f
(p,s)
is the average/best of objective func-
tion values found by variant s on problem p after 30
runs and f
w
is the worst objective function value of
problem p after 30 runs among all variants. Since
a zero value of min{m
(p,s)
: s ∈ S } may appear, the
performance ratios used in our comparative study are
defined (Vaz and Vicente, 2007) by
r
(p,s)
=
1+ m
(p,s)
− q if q ≤ 10
−5
m
(p,s)
q
otherwise,
where q = min{m
(p,s)
: s ∈ S }. Then ρ
s
(τ), the frac-
tion of problems for which the variant s has a perfor-
mance ratio r
(p,s)
within a factor τ, is given by
ρ
s
(τ) =
n
P
τ
n
P
where n
P
τ
is the number of problems in P with r
(p,s)
≤
τ and n
P
is the total number of problems in P . ρ
s
(τ)
is the probability (for variant s ∈ S ) that the perfor-
mance ratio r
(p,s)
is within a factor τ ∈ R of the best
possible ratio.
At first, we tested our program with the stochastic
ranking and the global competitive rankings for ob-
taining solutions of the above 13 constrained prob-
lems to check which technique is better than the oth-
ers in comparison. The variants were stochastic rank-
ing, global competitive ranking 1, with a fixed value
of P
f
, and global competitive ranking 2, with a ran-
dom value of P
f
in the interval (0, 0.45). Figure 2
shows the profiles of the performance metric f
avg
, the
average of the best solutions obtained over the 30
runs. If we are only interested in knowing which vari-
1.0 1.1 1.2 1.3 1.4 1.5 1.6
0.0
0.2
0.4
0.6
0.8
1.0
τ
ρ(τ)
Performance profile based on f_avg after 30 runs
Stochastic Ranking
Global Competitive Ranking 1
Global Competitive Ranking 2
Figure 2: Performance profile of average objective function
value for different variants.
ant is the most efficient, in the sense that it reaches the
best solutions mostly, we compare the values of ρ for
τ = 1, and find the highest value which is the prob-
ability that the variant will win over the remaining
ones. However, to know the robustness of variants,
we compare the values of ρ(τ) for large values of τ. It
means that variants with the largest probabilities ρ(τ)
for large values of τ are the most robust ones. In this
figure it is shown that variant global competitive rank-
ing 1 (for fixed value of P
f
) wins over the other two
variants of m-CDE.
1.0 1.1 1.2 1.3 1.4 1.5 1.6
0.0
0.2
0.4
0.6
0.8
1.0
Performance profile based on f_avg after 30 runs
τ
ρ(τ)
Feasibility and Dominance Rules
Stochastic Ranking
Global Competitive Ranking 1
Global Competitive Ranking 2
Figure 3: Performance profile of average objective function
value using fitness (5).
In the second experiment, we tested the follow-
ing four variants of m-CDE: feasibility and domi-
nance rules, stochastic ranking, global competitive
ranking 1 and global competitive ranking 2 (as pre-
viously defined). To be able to fairly compare with
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
48

Table 2: Experimental results of the 13 test problems by m-CDE1.
Prob. best worst avg. median std. dev. avg. vio. G
avg
g01 -15.0000 -15.0000 -15.0000 -15.0000 1.16E-06 0.00E+00 196
g02 -0.8036 -0.7926 -0.8007 -0.8036 4.95E-03 0.00E+00 1408
g03 -1.0000 -0.9998 -1.0000 -1.0000 3.90E-05 5.88E-09 1750
g04 -30665.5387 -30665.5387 -30665.5387 -30665.5387 2.38E-05 8.66E-09 1091
g05 5126.4978 5126.4986 5126.4979 5126.4978 1.83E-04 9.23E-09 1750
g06 -6961.8161 -6624.1610 -6950.5609 -6961.8161 6.16E+01 9.67E-09 1750
g07 24.2316 24.2319 24.2317 24.2316 7.44E-05 1.60E-09 1750
g08 -0.0958 -0.0958 -0.0958 -0.0958 2.71E-06 0.00E+00 42
g09 680.6301 680.6301 680.6301 680.6301 1.38E-06 0.00E+00 727
g10 7049.2533 7076.5860 7053.3441 7050.6330 6.99E+00 1.13E-09 1750
g11 0.7500 0.7670 0.7506 0.7500 3.11E-03 6.36E-09 158
g12 -1.0000 -1.0000 -1.0000 -1.0000 2.33E-06 0.00E+00 30
g13 0.0539 0.0539 0.0539 0.0539 3.53E-17 9.96E-09 1750
the variant feasibility and dominance rules, the other
variants were fairly modified. After the modified se-
lection step of the algorithm, the fitness function is re-
calculated now using (5) so that the best and the worst
target points of the populationare identified according
to the objective function and constraint violation val-
ues. Figure 3 shows the profiles of the performance
metric f
avg
for the four variants. In this figure it is
shown that variant global competitive ranking 1 here
also wins over the other three variants of m-CDE in
comparison.
From the above discussion it is clear that in both
cases the variant of m-CDE based on global competi-
tive ranking with fixed value of P
f
gave better perfor-
mance over the other ones. We also tested our m-CDE
with global dense ranking technique but the obtained
results were significantly worse than those obtained
by global competitive ranking technique.
4.2 Comparing with other Methods
We also compare our m-CDE (based on the global
competitive ranking with fixed value of P
f
) with the
stochastic ranking presented in (Runarsson and Yao,
2000) and the global competitive ranking presented
in (Runarsson and Yao, 2003). The authors proposed
these techniques based on a (30, 200) evolution strat-
egy. Here, the stochastic ranking technique is de-
noted by SRES and the global competitive ranking
technique is GRES. An adaptive penalty scheme for
constraint handling with dynamic use of variants of
differential evolution (DUVDE) (Silva et al., 2011)
is also used in the comparison. We set the same
value of maximum number of generations according
to (Runarsson and Yao, 2000; Runarsson and Yao,
2003). We set G
max
= 1750 for all the problems ex-
cept problem g12 for all the runs. G
max
= 175 was set
for g12. Here, we aim to get a solution within 0.001%
of the optimal solution f
opt
.
Firstly, we run all the 13 problems 30 times with
the global competitive ranking technique using modi-
fied constrained differential evolution. Here we iden-
tified f
min
and f
max
of the objective function based on
the current fitness function Φ
GR
at generation z. Then
elitism was performed to determine the f
best
. Here-
after we will denote this version by m-CDE1. We re-
port ‘best’, ‘worst’, ‘avg.’ (average), ‘median’ and
‘std. dev.’ (standard deviation) of the best objective
functions and ‘avg. vio.’ (average constraint viola-
tion) among all the 30 runs. The average number of
generations ‘G
avg
’ attained among the 30 runs is also
reported. These results are shown in Table 2.
Secondly, we run again all the 13 problems 30
times with the global competitive ranking technique
using modified constrained differential evolution, but
this time, both f
min
and f
max
are identified after recal-
culating the fitness of all individuals in the population
using function Φ
FD
, at each generation z. Then we
set f
best
= f
min
. Hereafter we will denote this version
by m-CDE2. We remark that m-CDE2 is the vari-
ant global competitive ranking 1 of the second expe-
rience reported in the previous subsection. The re-
sults are shown in Table 3. It is shown from Tables 2
and 3 that in almost all problems with respect to the
different objective function measures the results ob-
tained by m-CDE1 are relatively better than those of
m-CDE2.
Finally, to compare the results obtained by m-
CDE1, shown in Table 2, with DUVDE, SRES and
GRES, results of ‘best’, ‘avg.’ and ‘std. dev.’ of the
best objective functions among 30 runs are shown in
Table 4. These results are taken from the cited papers
(Silva et al., 2011), (Runarsson and Yao, 2000) and
(Runarsson and Yao, 2003) respectively. In m-CDE1,
we use the population size N dependent on the dimen-
sion of test problem and use the maximum number of
generations according to (Runarsson and Yao, 2000;
Runarsson and Yao, 2003), although in DUVDE the
GLOBAL COMPETITIVE RANKING FOR CONSTRAINTS HANDLING WITH MODIFIED DIFFERENTIAL
EVOLUTION
49
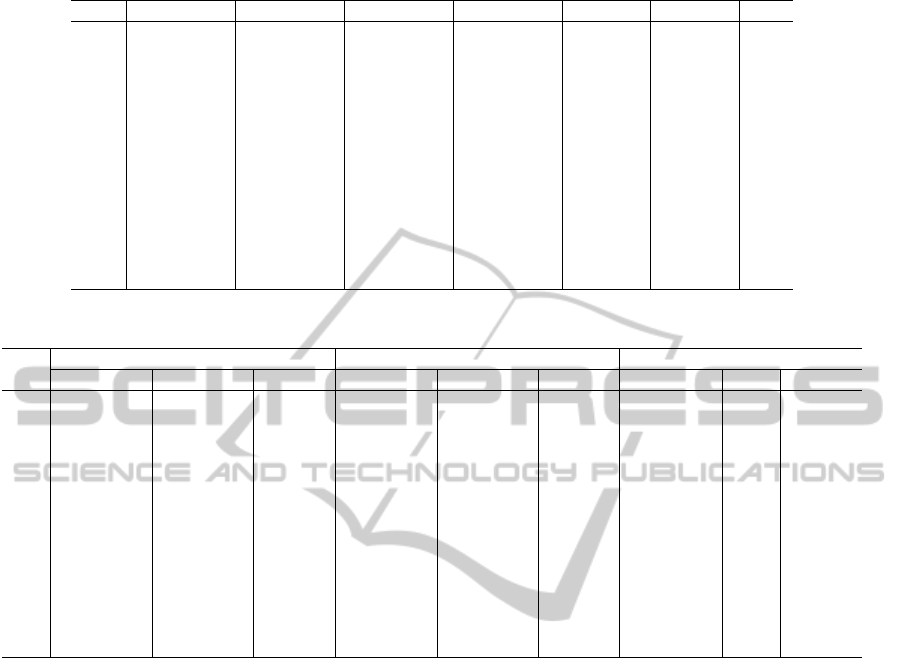
Table 3: Experimental results of the 13 test problems by m-CDE2.
Prob. best worst avg. median std. dev. avg. vio. G
avg
g01 -15.0000 -15.0000 -15.0000 -15.0000 1.22E-06 0.00E+00 196
g02 -0.8036 -0.7926 -0.8004 -0.8036 5.03E-03 2.07E-10 1438
g03 -1.0000 -0.9966 -0.9997 -0.9999 6.53E-04 4.54E-09 1750
g04 -30665.5387 -30665.5387 -30665.5387 -30665.5387 2.47E-05 8.24E-09 1039
g05 5126.4978 5126.4978 5126.4978 5126.4978 1.85E-12 1.00E-08 1750
g06 -6961.8161 -6615.7067 -6950.2790 -6961.8161 6.32E+01 9.94E-09 1695
g07 24.2316 24.2325 24.2318 24.2317 1.98E-04 1.75E-09 1750
g08 -0.0958 -0.0958 -0.0958 -0.0958 2.86E-06 0.00E+00 30
g09 680.6301 680.6301 680.6301 680.6301 1.10E-06 0.00E+00 730
g10 7049.2604 7250.9916 7100.8072 7051.2523 7.57E+01 1.38E-09 1750
g11 0.7500 1.0000 0.9353 1.0000 1.09E-01 1.74E-09 1515
g12 -1.0000 -1.0000 -1.0000 -1.0000 2.64E-06 0.00E+00 20
g13 0.0539 0.0539 0.0539 0.0539 1.14E-05 9.70E-09 1750
Table 4: Results from DUVDE, SRES and GRES.
Prob.
DUVDE SRES GRES
best avg. std. dev. best avg std. dev. best avg. std. dev.
g01 -15.0000 -12.5000 2.37E+00 -15.0000 -15.0000 0.00E+00 -15.0000 – 0.00E+00
g02 -0.8036 -0.7688 3.57E-02 -0.8035 -0.7820 2.00E-02 -0.8035 – 1.70E-02
g03 -1.0000 -0.2015 3.45E-01 -1.0000 -1.0000 1.90E-04 -1.0000 – 2.60E-05
g04 -30665.5000 -30665.5000 0.00E+00 -30665.5390 -30665.5390 2.00E-05 -30665.5390 – 5.40E-01
g05 5126.4965 5126.4965 0.00E+00 5126.4970 5128.8810 3.50E+00 5126.4970 – 1.10E+00
g06 -6961.8000 -6961.8000 0.00E+00 -6961.8140 -6875.9400 1.60E+02 -6943.5600 – 2.90E+02
g07 24.3060 30.4040 2.16E+01 24.3070 24.3740 6.60E-02 24.3080 – 1.10E-01
g08 -0.0958 -0.0958 0.00E+00 -0.0958 -0.0958 2.60E-17 -0.0958 – 2.60E-17
g09 680.6300 680.6300 3.00E-05 680.6300 680.6560 3.40E-02 680.6310 – 5.80E-02
g10 7049.2500 7351.1700 5.26E+02 7054.3160 7559.1920 5.30E+02 * – *
g11 0.7500 0.9875 5.59E-02 0.7500 0.7500 8.00E-05 0.7500 – 7.20E-05
g12 † † † -1.0000 -1.0000 0.00E+00 -1.0000 – 0.00E+00
g13 † † † 0.0539 0.0675 3.10E-02 0.0539 – 1.30E-04
(†) not considered; (–) not available; (*) not solved
authors used the population size 50 and the maximum
number of generations 3684 for all the tested prob-
lems. Problems g12 and g13 were not tested with
DUVDE (Silva et al., 2011). From Tables 2 and 4
we may conclude that for most of the problems, and
with respect to all measures of comparison, m-CDE1
performs rather well when compared with DUVDE,
SRES and GRES.
From the above discussion it is clear that the
proposed modified constrained differential evolution
based on the global competitive ranking technique to
handle constraints, is rather effective when converg-
ing to constrained global solutions.
5 CONCLUSIONS
In this paper, to make the DE methodology more ef-
ficient to handle the constraints in constrained global
optimization problems, a modified constrained differ-
ential evolution algorithm has been proposed. The
modifications focus on self-adaptive control param-
eters, modified mutation, modified selection and
elitism. Inversion operation has also been imple-
mented in the proposed m-CDE.
To conclude, we emphasize the modifications that
mostly influence the efficiency of the algorithm. The
mixed modified mutation, in the m-CDE algorithm,
aims at exploring both the entire search space (when
using the mutation proposed in (Kaelo and Ali, 2006))
and the neighbourhood of the best point found so far
(when using the best point as the base point cycli-
cally). The modified selection, to handle the con-
straints effectively, uses a fitness function based on
the global competitiveranking technique. In this tech-
nique, fitness of all target and trial points are cal-
culated all together after ranking them based on the
objective function and the constraint violation sepa-
rately, for competing in modified selection to decide
which points win for next generation population. This
technique seems to have stricken the right balance be-
tween the objective function and the constraint vio-
lation for obtaining a global solution while satisfying
the constraints.
To test the effectiveness of the new m-CDE, 13
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
50

benchmark constrained nonlinear programming prob-
lems have been considered. These problems have also
been solved with the stochastic ranking and the feasi-
bility and dominance rules techniques and compari-
son has been made based on their performance pro-
files. It is shown that m-CDE with the global com-
petitive ranking, based on a fixed value of P
f
, is rel-
atively better than the other two techniques. A com-
parison has also been made with other results from the
literature: the adaptive penalty-based differential evo-
lution, the stochastic ranking based on an evolution
strategy, and the global competitive ranking based on
an evolution strategy. It is shown that m-CDE is rather
competitive when compared with the other solution
methods. Future developments will focus on the ex-
tension of the m-CDE to problems with mixed integer
variables.
ACKNOWLEDGEMENTS
This work is supported by FCT (Fundac¸˜ao para a
Ciˆencia e a Tecnologia) and Ciˆencia 2007, Portugal.
We thank two anonymous referees for their valuable
comments to improve this paper.
REFERENCES
Ali, M. M., Khompatraporn, C. and Zabinsky, Z. B. (2005).
A numerical evaluation of several stochastic algo-
rithms on selected continuous global optimization test
problems. Journal of Global Optimization, 31, 635–
672.
Barbosa, H. J. C. and Lemonge, A. C. C. (2003). A new
adaptive penalty scheme for genetic algorithms. Infor-
mation Sciences, 156, 215–251.
Brest, J., Greiner, S., Boˇskovi´c, B., Mernik, M. and
ˇ
Zumer,
V. (2006). Self-adapting control parameters in differ-
ential evolution: a comparative study on numerical
benchmark problems. IEEE Transactions on Evolu-
tionary Computation, 10, 646–657.
Coello Coello, C. A. (2000). Constraint-handling using an
evolutionary multiobjective optimization technique.
Civil Engineering and Environmental Systems, 17,
319–346.
Coello Coello, C. A. and Cort´es, N. C. (2004). Hybridiz-
ing a genetic algorithm with an artificial immune sys-
tem for global optimization. Engineering Optimiza-
tion, 36, 607–634.
Deb, K. (2000). An efficient constraint handling method
for genetic algorithms. Computer Methods in Applied
Mechanics and Engineering, 186, 311–338.
Dolan, E. D. and Mor´e, J. J. (2002). Benchmarking opti-
mization software with performance profiles. Mathe-
matical Programming, 91, 201–213.
Dong, Y., Tang, J., Xu, B. and Wang, D. (2005). An appli-
cation of swarm optimization to nonlinear program-
ming. Computers & Mathematics with Applications,
49, 1655–1668.
Fletcher, R. and Leyffer, S. (2002). Nonlinear programming
without a penalty function. Mathematical Program-
ming, 91, 239–269.
Fourer, R., Gay, D. M. and Kernighan, B. W. (1993). AMPL:
A modelling language for matematical programming.
Boyd & Fraser Publishing Co.: Massachusets.
Hedar, A. R. and Fukushima, M. (2006). Derivative-free fil-
ter simulated annealing method for constrained con-
tinuous global optimization. Journal of Global Opti-
mization, 35, 521–549.
Holland, J. H. (1975). Adaptation in Natural and Artificial
Systems. University of Michigan Press: Ann Arbor.
Kaelo, P. and Ali, M. M. (2006). A numerical study of some
modified differencial evolution algorithms. European
Journal of Operational Research, 169, 1176–1184.
Ray, T. and Tai, K. (2001). An evolutionary algorithm with
a multilevel pairing strategy for single and multiob-
jective optimization. Foundations of Computing and
Decision Sciences, 26, 75–98.
Ray, T. and Liew, K. M. (2003). Society and civilization:
An optimization algorithm based on the simulation of
social behavior. IEEE Transactions on Evolutionary
Computation, 7, 386–396.
Rocha, A. M. A. C. and Fernandes, E.M.G.P. (2008). Feasi-
bility and dominance rules in the electromagnetism-
like algorithm for constrained global optimization.
In Gervasi et al. (Eds.), Computational Science and
Its Applications: Lecture Notes in Computer Science
(vol. 5073, pp. 768–783). Springer: Heidelberg.
Rocha, A. M. A. C. and Fernandes, E.M.G.P. (2009). Self
adaptive penalties in the electromagnetism-like algo-
rithm for constrained global optimization problems. In
Proceedings of the 8th World Congress on Structural
and Multidisciplinary Optimization (pp. 1–10).
Runarsson, T. P. and Yao, X. (2000). Stochastic ranking for
constrained evolutionary optimization. IEEE Transac-
tions on Evolutionary Computation, 4, 284–294.
Runarsson, T.P. and Yao, X. (2003). Constrained evolution-
ary optimization – the penalty function approach. In
Sarker et al. (Eds.), Evolutionary Optimization: Inter-
national Series in Operations Research and Manage-
ment Science (vol. 48, pp. 87–113), Springer: New
York.
Silva, E. K., Barbosa, H. J. C. and Lemonge, A. C. C.
(2011). An adaptive constraint handling technique for
differential evolution with dynamic use of variants in
engineering optimization. Optimization and Engineer-
ing, 12, 31–54.
Storn, R. and Price, K. (1997). Differential evolution – a
simple and efficient heuristic for global optimization
over continuous spaces. Journal of Global Optimiza-
tion, 11, 341–359.
Vaz, A. I. F. and Vicente, L. N. (2007). A particle swarm
pattern search method for bound constrained global
optimization. Journal of Global Optimization, 39,
197–219.
Zahara, E. and Hu, C.-H. (2008). Solving constrained op-
timization problems with hybrid particle swarm opti-
mization. Engineering Optimization, 40, 1031–1049.
GLOBAL COMPETITIVE RANKING FOR CONSTRAINTS HANDLING WITH MODIFIED DIFFERENTIAL
EVOLUTION
51
