SOME PROBLEMS HANDLED BY PARTICLE SWARM
OPTIMIZATION IN AUTOMATIC CONTROL
Guillaume Sandou
Supelec Systems Sciences (E3S), Automatic Control Department, 3, rue Joliot Curie, 91192 Gif-sur-Yvette, France
Keywords: Particle swarm optimization, Automatic control, PID tuning, H

synthesis.
Abstract: Most of the methods to design automatic control laws rely on the solution to optimization problems.
However, straightforward formulations of costs and constraints of these problems are mainly non convex,
non smooth or non analytic. That is why the classical approach is to simplify the problem so as to get
tractable and exactly solvable optimization problems. The use of direct methods such as metaheuristics is
underused in the control community. In this paper, a Particle Swarm Optimization method is used to solve
some complex initial problems found in the control field to show the interest in the use of such methods.
1 INTRODUCTION
Optimization has traditionally brought efficient
methods to compute control laws. However, the
traditional methodology is concerned with the
design of a simplified model of the plant to control.
In parallel, costs and constraints are reformulated so
as to express all specifications in a well suited
framework.
In the automatic control history, numerous
examples of this approach can be found: Linear
Quadratic methods, optimal control (Kwakernaak
and Sivan, 1972), H
2
or H

control design (Zhou et
al., 1996), predictive control (Maciejowski, 2002).
However, due to the necessity of this specific
structure of the optimization model, some of the
specifications cannot be directly taken into account
in the design process. They have to be a posteriori
checked during an analysis phase. This approach
may lead to some iteration between the synthesis
and the analysis phases.
Nowadays, three points have to be considered:
systems to be controlled are more and more
complex, specifications are more and more various
and precise, industries want to find best
performances. Corresponding optimization problems
are non convex, non differentiable, with numerous
local optima. In such a context, metaheuristic
optimization methods appear to be interesting
candidate methods to solve these kinds of problems.
In this paper, the main focus is on the use of Particle
Swarm Optimization method. The goal of this paper
is not to present new results (most of them have
already been published in the Automatic Control
field by the author) but to show to the metaheuristic
community that there is a large application field
where such algorithms are really underused and have
a great potential.
The paper is organised as follows. In section 2,
costs and constraints which are commonly
encountered in the Automatic Control domain are
called up. Two examples of the application of
Particle Swarm Optimization are then presented. In
section 3, the optimization of the tuning of
Proportional-Integral-Derivative (PID) controller is
performed. An advanced control methodology is
then studied in section 4, namely the H

synthesis
problem. Finally, conclusion remarks are drawn in
section 5.
2 COST AND CONSTRAINTS IN
AUTOMATIC CONTROL
Consider the generic closed loop framework of
figure 1. s is the Laplace variable.
System
)(sG ),( sθK
Controller
+
+
+
-
r
u v
y
d
ε
Figure 1: Classical closed loop framework.
315
Sandou G..
SOME PROBLEMS HANDLED BY PARTICLE SWARM OPTIMIZATION IN AUTOMATIC CONTROL.
DOI: 10.5220/0003672303150319
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 315-319
ISBN: 978-989-8425-83-6
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

A system
)(sG
has to be controlled. The control
input is
v and the output is
y
. The controller is
),(

sK and depends on tuning parameters

.
r
is
the reference and the disturbance is
d
. In this closed
loop, any transfer function from an input x to an
output z is a function of the parameters θ:
),()( θsHsT
zx


(1)
In the same way of thinking, any time response
)(tx
is a function of θ:
)[,0[),(),(,()(  ττdτrθftx
(2)
Some of the classical criterions in the case of Single
Input Single Output (SISO) are:
 Cut-off frequency:
1
10
,1),(s.t
minarg)(
1
ωωθωjT
ωθω
yε
ω



;
(3)
 Module margin:
)1(),(min)(Δ 

θωjTθm
yε
ω
;
(4)


H
norm of the system (computed for Multi
Inputs Multi Outputs system):
),(sup)( 

jT
yr



(5)
with:
)),(),((max
),(




jTjT
j
yryri
i




(6)
More generally, specifications can be given as
temporal templates for transfer function of the
system of figure 1. Some classical specifications are
given for the Heaviside step response. Once again,
all criterion are a function of

.

%α
time response:
 














trt
TtT
T
T
e
100/,
:\
inf)(
0


;
(7)

Maximum of the control input:
),(max)(
max
θtuθu
t

.
(8)
It appears that the mathematical expressions of these
constraints are often non smooth (computations of
min/max, absolute value, no analytical
expression...). Some classical approaches do exist to
compute a controller which satisfies a given set of
specifications. However, the problem is now not
only to satisfy a set of constraints, but to optimize
the performances of the system and to take into
account all constraints in the design procedure.
Finally, corresponding optimization problems are
hard to solve. That is why the use of metaheuristics
optimization methods appears as a very interesting
approach to explore.
3 PID TUNING AND
OPTIMIZATION
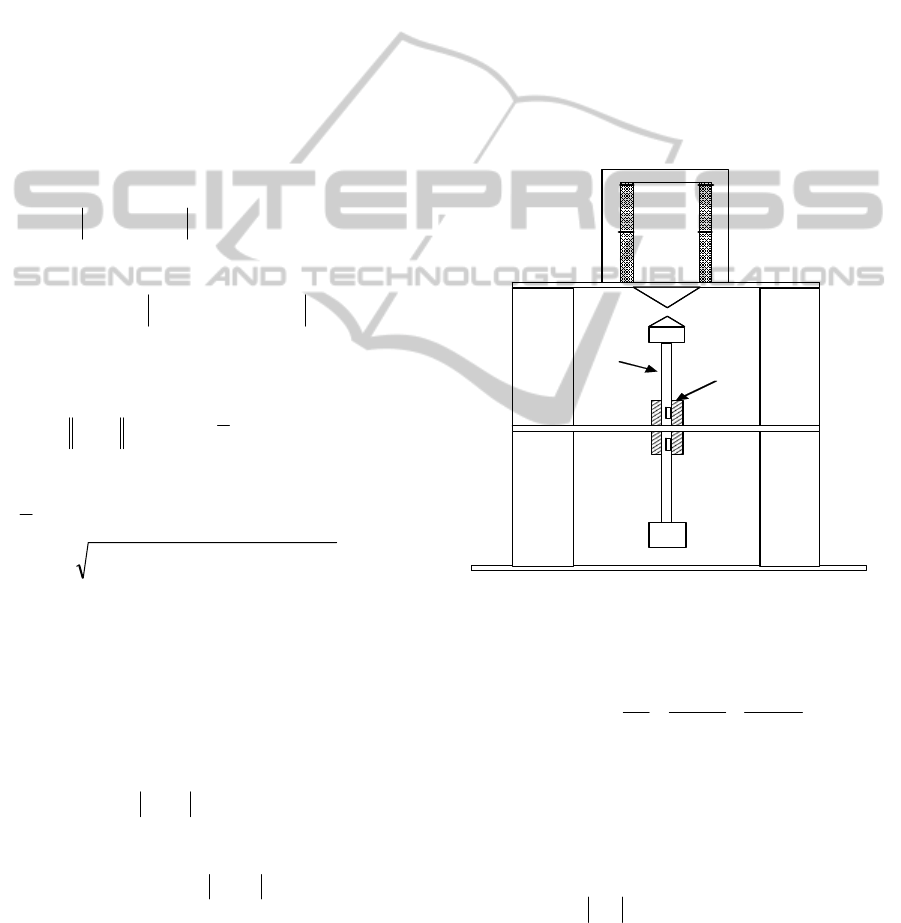
In this section, we want to optimize a PID controller
for a magnetic levitation, represented in figure 2.
Electric
magnet
Pendulum
Position
Figure 2: Magnetic levitation system.
To control the system, PID controller with high
frequencies filtering is used:
sTs
sT
sT
KsC
fd
d
i




1
1
)
1
1
1()(

,
with
10/
dd
T


.
(9)
The parameters of the optimization problem are:
T
fdi
TTTKθ ),,,( .
(10)
The specifications to be achieved are: control input
limitations:
V10)(max tu
, module margin:
5.0Δ m
, 5% time response as low as possible.
The problem can be expressed as the following
minimization problem:
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
316

 
2
2
1
21
0
)5.0)1()(min()(
:5.0)1()(minif
))10))((max(exp()(
:10))(max(if
)()(
100/5
:\
infmin


























jGJ
jG
tuJ
tu
JJ
trt
TtT
t
t
T
(11)
A Particle Swarm Optimization method is used to
solve the initial problem (Eberhart and Kennedy,
1995), with standard values of parameters (Kennedy
and Clerc, 2006). Statistical optimization results are
given in table 1. Computation times are 10 seconds
with Matlab 2007b on a Pentium IV, 2.0GHz.
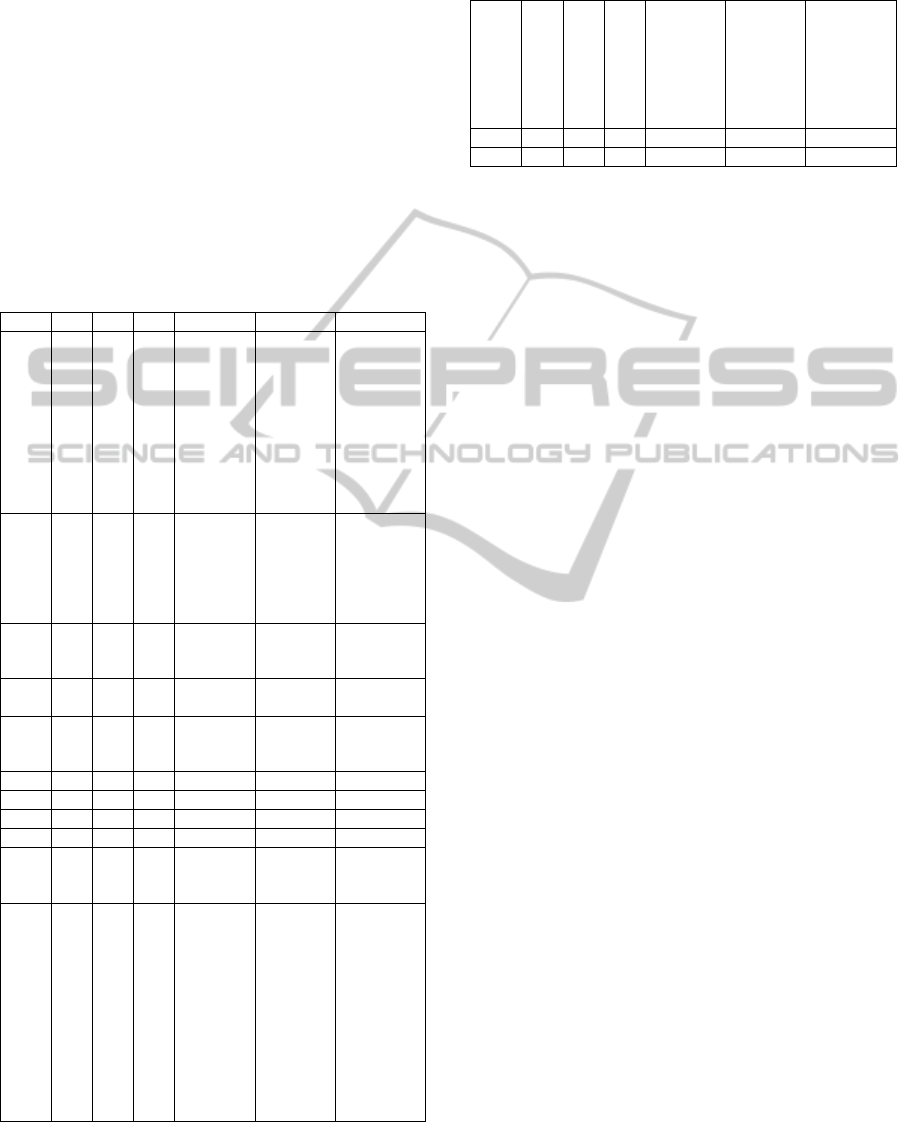
Table 1: Results for the time response minimization with
penalization on the control input and module margin.
Best Worst Mean Standard deviation
30.8 10
-3
s 39.7 10
-3
s 31.4 10
-3
s 1.1 10
-3
s
4 REDUCED ORDER H

SYNTHESIS
4.1 Problem Statement
H

synthesis is an efficient tool in automatic control
to compute controllers in a closed-loop framework,
achieving high and various performances (Gahinet
and Apkarian, 1994); (Zhou et al., 1996).
H

synthesis relies on the reformulation of the
closed loop problem of figure 1 into a standard form
corresponding to the block diagram of figure 3.
Figure 3: Standard form of a closed loop.
The idea of H

synthesis is to solve the following
optimization problem:


)(min
)(
sT
zw
sK
.
(12)
This optimization problem can easily be solved as it
can be expressed either by a Linear Matrix
Inequality (LMI) problem (Zhou et al., 1996). The
main drawback is the controller order: the controller
computed by the H

synthesis procedure has the
same order of the synthesis model.
To get low order controllers, matrices rank
constraints can be added, leading to Bilinear Matrix
Inequality (BMI) problems and so to non-convex
ones. More recently, some new techniques have
began to emerge, adding some random process in the
deterministic search algorithm (Arzelier, et al.,
2010), and achieving results which are almost
similar to those obtained with the HIFOO standard
(Burke, et al., 2006).
Consider the state space representation of the
plant
)(sP
of figure 3:









)()()(
)()()()(
)()()()(
:
21
12111
1
twtxty
tutwtxtz
tutwtxtx
DC
DDC
BBA

,
(13)
In this paper, we look for a static feedback:
)()( tytu
K

,
(14)
where
K
is a constant matrix of gains. This closed
loop is stable if and only if:

 )( BKCA
,
(15)
where

 )(M
denotes the spectrum of M .
Considering the direct solution to the optimal H

static output feedback, the problem finally refers to
the following optimization problem:










)(
)()(
..
)(min
BKCA
K
K
tytu
ts
sT
zw
rm
,
(16)
This kind of criterion can be optimized by PSO
which does not require any particular formulation of
the cost function. Finally, the design of an H

static
output feedback relies on the tuning of a matrix
rm
K and so to the tuning of
r
m  variables.
For this possibly relatively large scale problem, we
use the algorithm given in (van den Bergh and
Engelbrecht, 2002).
4.2 Numerical Results
For comparison, the algorithm is tested on the
benchmark examples given in the COMPleib library
(Leibfritz, 2004).
Results obtained with the PSO algorithm have
been compared with those obtained with the HIFOO
)(sP
)(sK
)(tw
)(t
z
)(ty
)(tu
SOME PROBLEMS HANDLED BY PARTICLE SWARM OPTIMIZATION IN AUTOMATIC CONTROL
317

package (Burke, et al. 2006), which is a
deterministic solver and considered as one of the
best effective tool for the synthesis of static output
feedback, and those obtained in (Arzelier, et al.,
2010). Corresponding results are given in table 2.
5 CONCLUSIONS
Optimization has always played an important role in
the field of Automatic Control. Indeed, most of the
existing control design methodologies are concerned
with the solution to optimization problems.
Table 2: Computation of H

static output feedbacks.
Ex.
n m r HIFOO Ar. et al PSO
A1
A2
A5
A9
A10
A11
A12
A13
A14
A18
5
5
4
10
55
5
4
28
40
10
3
3
2
4
2
2
3
3
3
2
3
3
2
5
2
4
4
4
4
2
4.14 10
-7
0.1115
669.56
1.0029
Inf
2.8335
0.3120
163.33
101.7203
12.6282
1.76 10
-
6
0.1115
661.7
1.0061
Inf
2.8375
0.6165
395.0404
319.31
10.6214
4.7 10
-
22
0.1115
665.09
1.098
Inf
2.8609
0.3134
167.36
101.96
27.18
H1
H3
H4
H5
H6
H7
4
8
8
4
20
20
2
4
4
2
4
4
1
6
6
2
6
6
0.1539
0.8061
22.8282
8.8952
192.3445
192.3885
0.1538
0.8291
22.8282
17.6061
401.7698
353.9425
0.1529
0.8399
23.43
10.0031
195.86
194.24
D2
D4
D5
3
6
4
2
4
2
2
6
2
1.0412
0.7394
1035.5
1.0244
0.7404
1030.82
1.0255
0.7863
1028
J2
J3
21
24
3
3
3
6
183.3512
5.0963
365.09
9.194
192.17
5.138
R1
R2
R3
4
4
12
2
2
1
3
2
3
0.8694
1.1492
74.2513
0.8661
1.1482
74.2513
0.8738
1.1451
74.2513
W1
10 3 4 4.0502 4.1055 6.4843
B2
82 4 4 0.6471 2.90 1.0345
S
60 2 30 0.0201 0.02 0.0200
P
5 1 3 32.2258 0.0087 0.0571
T1
T2
T3
7
7
7
2
2
2
4
3
3
0.3736
5200
0.4567
0.3799
5200
0.3264
0.4038
5200
0.5829
N1
N2
N5
N6
N7
N9
N12
N13
N14
N15
N16
N17
3
2
7
9
9
5
6
6
6
3
8
3
1
1
1
1
1
3
2
2
2
2
4
2
2
1
2
4
4
2
2
2
2
2
4
1
13.9089
2.2216
266.54
5602
74.0757
28.6633
16.3925
14.0589
17.4778
0.0982
0.9556
11.2182
13.458
2.2050
266.5445
5602
74.0372
31.03
16.3116
14.0579
17.4757
0.0980
0.9556
11.2182
13.8189
2.2049
266.4023
5593
74.0326
30.1549
17.7568
14.4829
17.5063
0.0980
0.9560
11.4864
Table 2: Computation of H

static output feedbacks.
(cont.)
F10
F11
F14
F15
F16
F17
F18
5
5
5
5
5
5
5
2
2
2
2
2
2
2
3
3
4
4
4
4
2
79853
7719
53156
17521
44432
30024
124.7259
82314
78248
557008
202610
465790
303380
154.9970
80658
77213
535040
178900
447500
300240
126.6402
TM
6 2 4 2.5267 2.1622 2.8015
FS
5 1 3 96925 87160 84727
However, in the classical approach, particular
expressions and reformulation of initial costs and
constraints functions are used to get an optimization
problem which can be exactly solved. To capture the
difficulties of the initial optimization problems an
underused approach relies on the use of stochastic
algorithms which are able to deal with whatever
costs and constraints. In this paper, the main focus is
on the use of Particle Swarm Optimization algorithm
to solve some generic Automatic Control problems:
PID optimization, and reduced order H

synthesis.
All these results are much than satisfactory, showing
the interest of using such algorithms, as results are
quite similar to standard deterministic algorithms.
Finally, Automatic Control appears as a large,
mostly unexplored, field of applications for the
metaheuristic community.
REFERENCES
Arzelier, D., Gryazina, E. N., Peaucelle, D., Polyak, T.,
2010. Mixed LMI/Randomized methods for static
output feedback control design. In: Proceedings of the
IEEE American Control Conference, Baltimore, USA.
Burke, J. V., Henrion, D., Lewis, A. S., Overton M. L.,
2006. HIFOO - A Matlab package for fixed-order
controller design and H

optimization. In:
Proceedings of the IFAC Symposium on Robust
Control Design, Toulouse.
Eberhart, R. C., Kennedy, J., 1995. A new optimizer using
particle swarm theory. In Proc. of the Sixth
International Symposium on Micromachine and
Human Science, Nagoya, Japan. pp. 39-43.
Gahinet, P., Apkarian, P., 1994. A linear matrix inequality
approach to H

control. In: Int. Journal of Robust and
Nonlinear Control, vol. 4, pp. 421-448.
Kennedy, J., Clerc, M., 2006. Standard PSO.
http://www.particleswarm.info/Standard_PSO_2006.c.
Kwakernaak, H., Sivan, R., 1972. Linear optimal control
New York: Willey-interscience.
Leibfritz, F., 2004. COMPleib: COnstraint Matrix-
optimization Problem library - a collection of test
examples for nonlinear semidefinite programs, control
system design and related problems. Technical report.
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
318

University of Trier, Department of Mathematics, URL:
www.complib.de.
Maciejowski, M., 2002.. Predictive Control with
Constraints. Prentice Hall, England.
Van den Bergh F., Engelbrecht A. P., 2002. A new locally
convergent particle swarm optimiser. In: Proceedings
of the IEEE Conference on Systems, Man and
cybernetics, Hammamet, Tunisia.
Zhou, K., Doyle, J. C., Glover, K., 1996. Robust and
optimal control, New Jersey: Prentice-Hall.
SOME PROBLEMS HANDLED BY PARTICLE SWARM OPTIMIZATION IN AUTOMATIC CONTROL
319