
AN ALGORITHM FOR SATISFIABILITY DEGREE
COMPUTATION
∗
Jian Luo, Guiming Luo and Mo Xia
Key Laboratory for Information System Security, Ministry of Education
Tsinghua National Laboratory for Information Science and Technology, School of Software
Tsinghua University, Beijing 100084, China
Keywords:
Satisfiability degree, Propositional logic, Time complexity, Unit clause.
Abstract:
Satisfiability degree describes the satisfiable extent of a proposition based on the truth table by finding out the
proportion of interpretations that make the proposition true. This paper considers an algorithm for computing
satisfiability degree. The proposed algorithm divides a large formula into two smaller formulas that can be
further simplified by using unit clauses; once the smaller formulas contains only a clause or unit clauses, their
satisfiability degrees can be directly computed. The satisfiability degree of the large formula is the difference
of the two smaller ones. The correctness of the algorithm is proved and it has lower time complexity and space
complexity than all the existing algorithms, such as the enumeration algorithm, the backtracking algorithm,
the propositional matrix algorithm and so on. That conclusion is further verified by experimental results.
1 INTRODUCTION
The concept of satisfiability degree, a new logic, was
proposed in (Luo and Hu, 2009) to interpret the truth
value of a formula. It extends the concept of satis-
faction propositions and describes how satisfactory
is based on the proportion of interpretations under
which the formula is true.
Satisfiability degree differs in basic ways
from fuzzy logic (Zadeh, 1965) and probabilistic
logic (Gerla, 1994). In fuzzy logic (Zhou and Wang,
2006), every formula interpretation is not precise. In
probabilistic logic, the distribution function or the
density function of random variables must be known.
Thus, both fuzzy logic and probabilistic logic cannot
give reasonable interpretations when a formula in
based on logic operations. Satisfiability degree is
totally based on logic theory with the truth of a
proposition based on an overall perspective and the
behavior of the logic operators. Thus, satisfiability
degree is an inherent attribute of the proposition, not
depending on the interpretation of the proposition.
Satisfiability degree can be used for prediction,
reasoning, model checking and so on. For instance,
model checking only can tell us whether a system
satisfies a property or not; but some tolerable sys-
∗
This work is supported by the Funds NSFC 60973049,
60635020, and TNList cross-discipline foundations.
tems can partially satisfy properties, which can be de-
scribed by satisfiability degree.
There are four algorithms for satisfiability degree
computation: the basic enumeration algorithm has
O(m· 2
n
) time complexity even some pruning can be
utilized to reduce unnecessary costs; the XOBDD al-
gorithm (Luo and Hu, 2009) uses a ordered binary de-
cision diagram with weighted assigned, XOBDD for
short, to represent a Boolean formula. The satisfia-
bility degree is computed by recursively merging the
Boolean operators. Howeverit may cause the state ex-
plosion problem with the size of the graph increasing;
the backtracking search algorithm (Yin and Hu, 2009)
bade on SAT method (McMillan, 2002) (Malik and
Fu, 2005) also has exponential time complexity and it
sometimes take more time than the simulation method
once the formula contains many clauses; although the
propositional matrix search algorithm (Luo and Luo,
2010) can reduce the computation times efficiently, it
needs large space.
So, a new algorithm is proposed in this paper for
effectively computing satisfiability degree. It divides
a large formula into two smaller ones, and then uses
unit clauses to further simplify them so that the size
of the formula can be reduced. As long as the smaller
formulas only contains one clause or unit clauses,
the algorithm directly computes their satisfiability de-
grees, the difference of which equals the satisfiability
501
Luo J., Luo G. and Xia M..
AN ALGORITHM FOR SATISFIABILITY DEGREE COMPUTATION.
DOI: 10.5220/0003673205010504
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 501-504
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

degree of the large formula. The correctness of the al-
gorithm was proved and the order of time complexity
is lower than those of the existing algorithms. Exper-
imental results shows that the proposed algorithm is
more effective.
2 SATISFIABILITY DEGREE
Let P denote the set of all propositional formulas and
Ω the global field for interpreting P, for any formula
φ ∈ Ω and ω ∈ Ω, φ(ω) ∈ {0, 1}, we define a subset
Ω
φ
⊆ Ω such that:
Ω
φ
= {ω|φ(ω) = 1, ω ∈ Ω} (1)
Definition 1. Give the formal set P and the global
interpreting field Ω, the subset Ω
φ
is defined above.
Then, the function f : P → [0, 1] is called the satisfi-
ability degree on Ω, if for any formula φ ∈ P:
f(φ) =
d(Ω
φ
)
d(Ω)
(2)
where d(X) denotes the cardinality of set X.
Theorem 1. Given any propositional formulas ϕ and
φ, then:
f(ϕ∨ φ) + f(ϕ∧ φ) = f(ϕ) + f(φ) (3)
Theorem 1 can be proved by the Inclusion-
Exclusion Principle and it is the basis of the research
in subsequent.
Theorem 2. Given a CNF (Huth and Ryan, 2005)
formula C = D
1
∧ D
2
·· · ∧ D
m
, its satisfiability degree
can be computed as:
f(C) = f(D
2
∧· ··∧ D
m
)− f(
¬
D
1
∧D
2
·· · ∧ D
m
) (4)
The reason why we transform formulas in CNF
is that it is very easy to check validity. If a clause
contains only one literal, it is called unit clause.
3 ALGORITHM
In our algorithm, a CNF formula is presented by a set,
whose elements are also sets expressing its clauses.
Example 1. C = (p∨ q) ∧ (
¬
q∨r) ∧ (
¬
p∨q∨ r) can
be written as {{p, q}, {
¬
q, r}, {
¬
p, q, r}}, denoted as
C in the form of set.
If C
1
and C
2
are the independent formula-
pair (Luo and Hu, 2009), we have:
f(C
1
∧C
2
) = f(C
1
) · f(C
2
) (5)
The pseudo code for computing the independent
formula-pair is given bellow.
Algorithm 1: Independent formulas.
Require: a CNF formula C in set.
Ensure: formula-pair C
1
and C
2
satisfy C
1
∪C
2
≡ C
1: C
1
←
/
0
2: while c ∈ C and c is a unit clause do
3: C ← C \ {c} // remove c form set C.
4: for all c
∗
∈ C do
5: if c ⊆ c
∗
then
6: C ← C \ {c
∗
} // remove c
∗
form set C.
7: end if
8: if
¬
c ⊆ c
∗
then
9: c
∗
← c
∗
\
¬
c //
¬
c is a unit clause.
10: if c
∗
=
/
0 then
11: return
/
0 // This means C = ⊥.
12: end if
13: end if
14: end for
15: C
1
← C
1
∪ {c
∗
}
16: end while // while loop ends until no unit clauses.
17: C
2
← C
18: return C
1
and C
2
Algorithm 1 obtains the independent formula-pair
using unit clauses, which is a feedback process. Be-
cause the intermediate results may still have unit
clauses that will be checked by the while loop. The
procedure must terminate on correct input, because it
has no more than n cycles in the while loop if n is
the number of atoms in C. Because a formula cannot
be always divided into smaller independent ones, we
used unit clauses to do that.
Now we can use Theorem 2 to compute satisfiabil-
ity degree of any CNF formulas. As discussed above,
the computation times is determined by the dividing
criterion, thus we choose the clause with most literals
as the criterion such that the new formula can utilize
more unit clauses to reduce the formulas size. The
pseudo code is provided as bellow for computing sat-
isfiability degree of a CNF formula.
Algorithm 2: S-Degree.
Require: a CNF formula C in set form.
Ensure: the satisfiability degree f of C
1: if C =
/
0 then
2: f ← 0 //
/
0 means contradiction
3: else if all elements in C are unit clauses then
4: f ←
1
2
s
// s is the number of unit clauses in C.
5: else if formula C contains only a clause then
6: f ← 1−
1
2
t
// t is the number of atoms in C.
7: else
8: choose the clause c with most literals from C
9: C ← C \ {c}
10: [C
1
, C
2
] ← Independent formulas ({
¬
c} ∪C)
11: f ←S-Degree(C)S-Degree(C
1
)·S-Degree(C
2
)
12: end if
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
502

13: return f
Algorithm 2 is a recursive computation process,
but not to cause an infinite loop; because the size of
the formulas will smaller and smaller.
4 COMPLEXITY ANALYSIS
Suppose the considered CNF formula C = D
1
∧
D
2
·· · ∧ D
m
has n atoms and m clauses. We use
T(m, n) to denote the computation time for comput-
ing satisfiability degree and estimate its order to ob-
tain the worst time complexity. Algorithm 2 contains
a recursive call to itself, so its running time can often
be described by a recurrence, an equation or inequal-
ity.
As we choose the clause with most literals as di-
viding criterion, then the clause at least has ⌈
n
m
⌉ lit-
erals by the pigeonhole principle. By Theorem 2,
the satisfiability degree of C is determined by D
2
∧
D
3
·· · ∧ D
m
and
¬
D
1
∧ D
2
·· · ∧ D
m
; the former has
m− 1 clauses and at most n− 1 atoms while the latter
has at least ⌈
n
m
⌉ unit clauses; and it will be simplified
by Algorithm 1 to get the independent formula-pair
C
1
and C
2
. The Algorithm 2 executes ⌈
n
m
⌉ · (m − 1)
operations in the worst case; otherwise the more op-
erations, the smaller size of C
2
, which contradicts the
assumption, for considering the worst case. And C
1
can be directly computed, and C
2
has at most m − 1
clauses and no more than n− ⌈
n
m
⌉ atoms. As a result,
we have the following recurrence:
T(m, n) ≤ T(m− 1, n− 1)+ T(m− 1, n − a) + b (6)
where a = ⌈
n
m
⌉, and b = a · (m− 1).
We use the equivalent thinking method for solving
the recurrence (6) and establish its upper bound. It ba-
sic idea is that it is easier to compute the satisfiability
degree of a smaller formula than that of a large one.
Thus, we have the following inequality:
∃ε ∈ (0, 1) T(m− 1, n− a) ≤ε· T(m− 1, n− 1) (7)
Note that if a = 1, which means all elements in C
2
are unit clauses, then its satisfiability degree can be di-
rectly computed. Thus, the parameter ε < 1. Now we
can determine an upper bound on the recurrence (6)
by using recurrence (7).
Theorem 3. Algorithm 2 has O(α
min(m,n)
) time com-
plexity for computing the satisfiability degree of a
CNF formula with m clauses and n atoms, where
α ∈ (1, 2).
Proof. By the relation (7) and the recurrence (6),
T(m, n)≤T(m−1, n−1)+ε · T(m−1, n−a) + b
≤(1+ ε)T(m− 1, n− 1) + b
<(1+ ε)T(m− 1, n− 1) + c
<(1+ε)
2
T(m−2, n −2)+(1+ε)(c−2)+ c
· · ·
≤(1+ε)
t
T(m−t, n−t)+
t−1
∑
i=0
(1+ε)
i
(c− 2i)
If t = min(m, n), then Algorithm 2 stops since all the
formulas are empty sets. Then taking the higher order
term, we get O(α
min(m,n)
) as the upper bound for the
time complexity, where α = 1+ ε and α ∈ (1, 2), for
ε ∈ (0, 1).
In the above proof, we use the following conclu-
sions, i.e.,
c = n + m (8)
b = a· (m− 1) ≤ (
n
m
+ 1) ∗ (m− 1) < c (9)
t−1
∑
i=0
(1+ε)
i
(n+m−2i) <
(1+ε)
t
[ε(c−2t)+ 4]
ε
2
(10)
Table 1: Complexity Comparison of Algorithms.
Algorithms time complexity space complexity
EA
b
O(m· 2
n
) O(2
n
)
XA O(2
n
) O(2
n
)
BA O(2
n
) O(mn)
MA O(2
min(m,n)
) O(mn)
A2 O(α
min(m,n)
)
a
≤ O(mn)
a
m is the number of clauses and n is the number of atoms
and α ∈ (1, 2).
b
EA short for enumeration algorithm, XA for XOBDD al-
gorithm, BA for backtracking algorithm, MA for matrix
algorithm and A2 for Algorithm 2.
The comparison of time and space complexity
with Algorithm 2 and the other four algorithms are
described in Table 1. In terms of both time complex-
ity and space complexity, Algorithm 2 is superior to
the others.
5 EXPERIMENTAL RESULTS
Table 2 lists the run time for each algorithm. The enu-
meration algorithm, marked as EA, utilize the truth
table to compute satisfiability degree, so it runs very
slowly when the formula size is large, see Table 2 for
more details. Although some optimizations can make
the XOBDD algorithm, marked as XA, generally run
AN ALGORITHM FOR SATISFIABILITY DEGREE COMPUTATION
503
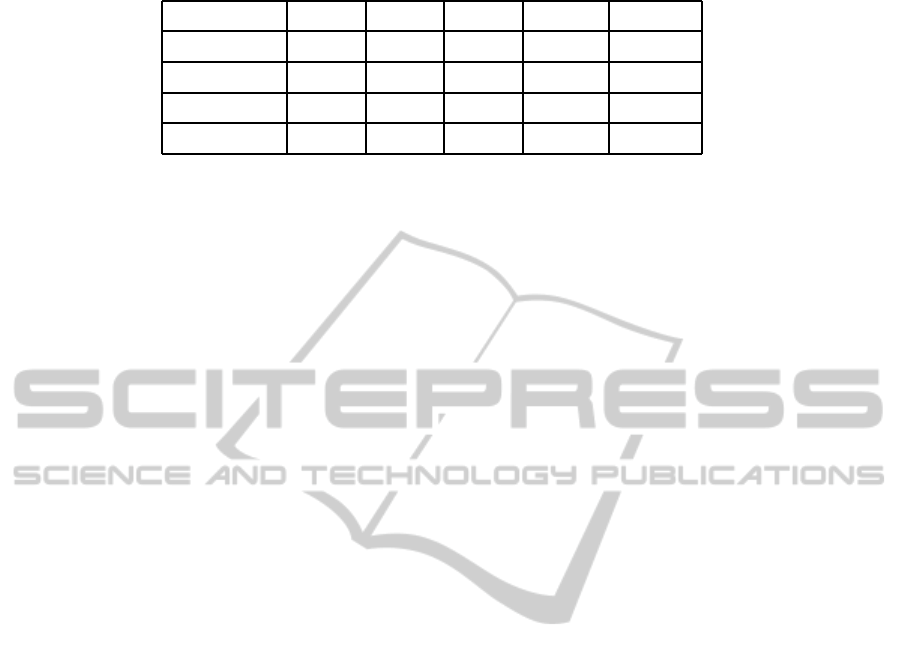
Table 2: The Run Time of each algorithm.
formula size EA XA BA MA A2
172× 164 > 24 h > 24 h > 24 h 0.1 s
a
0.04 s
169× 169
b
> 48 h
c
> 48 h > 48 h 71.8 s 1.2 s
2437× 852 > 48 h > 48 h > 48 h 11412 s 1080.4 s
2281× 1763 > 48 h > 48 h > 48 h 12000 s 932.4 s
a
h means hours and s for seconds.
b
The term ”169× 169” means 169 clauses and 169 atoms.
c
The term ”> 48 h” means that it takes at least 48 hours to solve the
problem, and so on.
in time less than 2
n
, it is an unsuitable approach; be-
cause sometimes those optimizations cannot reduce
computation times, not to mention its space explo-
sion problem. The backtracking depth will increase
for lager formulas, so it slows the backtracking algo-
rithm down. The backtracking search algorithm ver-
sion is marked as BA. The propositional matrix algo-
rithm, marked as MA, is more effective than the three
algorithm just mentioned before, since it analyzes the
structure of the formula to divide large formulas into
smaller ones such that their satisfiability degrees can
be easily obtained; but it needs more space and its rum
time is higher than Algorithm 2, because the number
of smaller formulas divided by Algorithm 2 is less.
Besides, Algorithm 2 needs less space than other four
alogrithms.
In all, the experimental results verify and support
the theoretical analysis in section 4.
6 CONCLUSIONS
Satisfiability degree is a new method to precisely in-
terpret the truth value of propositional logic. An algo-
rithm to computed satisfiability degree was proposed.
It divides a large formula into two smaller formu-
las; and they can be further simplified by unit clauses
such that their satisfiability degrees can be easily ob-
tained once they contain only a clause or only unit
clauses. The satisfiability degree of the large formula
equals the difference of the two formulas. The cor-
rectness of the proposed algorithm was proved as well
as α
min(m,n)
time complexity, where α is greater than 1
but smaller than 2. Thus, Algorithm 2 has a less time
complexity than the enumeration algorithm, XOBBD
algorithm and the search algorithms. In addition, Al-
gorithm use a set to represent a CNF formula such
thats pace consumed is greatly reduced. Because it
only need to store the atoms in the considered formula
not the interpretations. Experimental results further
demonstrates that conclusion.
Further work can apply satisfiability degree to pre-
diction, model checking and reasoning. We also in-
tend to use satisfiability degree to analyze the satis-
fiable extent of predicate logic, higher order logic as
well as temporal logic. By experimental results, sat-
isfiability degree can be used for circuit test.
REFERENCES
Gerla, G. (1994). Inferences in probability logic. In Artifi-
cial Intelligence. vol. 70, no. 1-2, 1994, pp. 33-52.
Huth, M. and Ryan, M. (2005). Logic in Computer Science.
China Machine Press, Beijing, 2nd edition.
Luo, J. and Luo, G. M. (2010). Propositional matrix search
algorithm for satisfiability degree computation. In the
9th IEEE International Conference on Cognitive In-
formatics. Beijing, China, pp.974-977.
Luo, G. M., Y. C. Y. and Hu, P. (2009). An algorithm for
calculating the satisfiability degee. In proceedings of
the 2009 sixth international Conference on Fuzzy Sys-
tem and Knowledge Discovery. Tianjin, China, 2009,
pp.322-326.
Malik, S., M. Y. and Fu, Z. (2005). Zchaff2004: An efficient
sat solver. In in LNCS 3542, Theory and Applications
of Satisfiability Testing. pp. 360C375.
McMillan, K. L. (2002). Applying sat methods in un-
bounded symbolic model checking. In in Proc. Int.
Conf. Computer-Aided Verification. vol.2404.
Yin, C. Y., L. G. M. and Hu, P. (2009). Backtracking
search algorithm for satisfiability degree calculation.
In proceedings of the 2009 sixth international Con-
ference on Fuzzy System and Knowledge Discovery.
Tianjin,China,2009,pp.3-7.
Zadeh, L. A. (1965). Fuzzy sets. In Information & Control.
vol. 8, no. 3, 1965, pp. 338-353.
Zhou, H. J. and Wang, G. J. (2006). A new theory
consistency index based on deduction theorems in
several logic systems. In Fuzzy Sets and Systems.
vol.157, no.3, pp.427-443.
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
504
