SYNTHESIZING PHEROMONE AGENTS FOR SERIALIZATION

IN THE DISTRIBUTED ANT COLONY CLUSTERING

Munehiro Shintani

, Shawn Lee

, Munehiro Takimoto

and Yasushi Kambayashi

Department of Information Sciences, Tokyo University of Science, Tokyo, Japan

Department of Computer and Information Engineering, Nippon Institute of Technology, Miyashiro, Japan

Keywords:

Mobile agent, Ant colony clustering, Intelligent robot control.

Abstract:

This paper presents effective extensions of our previously proposed algorithm for controlling multiple robots.

The robots are connected by communication networks, and the controlling algorithm is based on a speciﬁc

Ant Colony Clustering (ACC) algorithm. Unlike traditional ACC, we implemented the ants as actual mobile

software agents that control the mobile robots which are corresponding to objects. The ant agent migrates

among robots to look for an available one. Once the ant agent ﬁnds an available robot, the robot physically

moves along the instructions of the ant agent, instead of being conveyed. We also implemented pheromone

as mobile software agents, which attract many robots to some clusters by diffusing themselves through the

migration, so that the pheromone agents enable the robots to be efﬁciently assembled. In our new approach,

we take advantage of the pheromone agents not only to assemble the robots but also to serialize them. The

serializing property is desirable for particular applications such as gathering carts in the airports. We achieve

the property through migrations of the pheromone agents within a cluster and synthesizing them. We have

built a simulator based on our algorithm, and conducted numerical experiments to demonstrate the feasibility

of our approach.

1 INTRODUCTION

When we pass through terminals of the airport, we

often see carts scattered in the walkway and laborers

manually collecting them one by one. It is a laborious

task and not a fascinating job. It would be much easier

if carts were roughly gathered in any way before the

laborers begin to collect them.

In order to achieve such clustering, we have taken

advantage of the Ant Colony Clustering (ACC) algo-

rithm which is an Ant Colony Optimization (ACO)

specialized for clustering objects. ACO is a swarm

intelligence-based method and a multi-agent sys-

tem that exploits artiﬁcial stigmergy for the solu-

tion of combinatorial optimization problems. ACC

is inspired by the collective behaviors of ants, and

Deneubourg formulated an algorithm that simulates

the ant corps gathering and brood sorting behaviors

(Deneubourg et al., 1991). In ACC, artiﬁcial ants col-

lect objects that are scattered in a ﬁeld, imitating the

real ants, so that several clusters are gradually formed.

In traditional ACC, imaginary ants convey imaginary

objects for classifying them based on some similar-

ities, but in our algorithm, we implemented the ants

as actual mobile software agents that control the mo-

bile robots which are corresponding to objects. The

ant agent migrates among robots to look for an avail-

able one. Once the ant agent ﬁnds the available robot,

the robot physically moves along the instructions of

the ant agent, instead of being conveyed. The con-

trol manner contributes to suppressing total time cost

and energy consumption of the system. Because both

the time cost and energy consumption of migrations

of ant agents are negligible compared to the physical

movements of mobile robots.

We previously proposed an ACC approach using

mobile software agents. We call it distributed ACC

(Mizutani et al., 2010; Oikawa et al., 2010). In the

approach, some Ant agents, which is mobile soft-

ware agents corresponding to ants, iteratively traverse

robots, which correspond to objects picked up by ants.

Once the Ant agent migrates to a free robot with no

other task, it randomly drives the robot as shown by

1 of Figure 1. If the robot reaches another robot as

shown by 2 of Figure 1, an Ant agent locks its robot,

and leaves it to look for another free robot. In the

approach, the pheromone is also implemented as a

collection of mobile software agents. We call them

Pheromone agents. Each Pheromone agent is created

by an Ant agent on a robot included in a cluster. Once

it is created on the robot, it duplicates itself and makes

the clone migrate to other robots within the scope to

220

Shintani M., Lee S., Takimoto M. and Kambayashi Y..

SYNTHESIZING PHEROMONE AGENTS FOR SERIALIZATION IN THE DISTRIBUTED ANT COLONY CLUSTERING.

DOI: 10.5220/0003673302200226

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 220-226

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: The outline of the previous algorithm.

disseminate its effect. The Pheromone agent has a

vector datum representing strength and direction of its

attractiveness, which is used for guiding Ant agents as

shown by 3 of Figure 1. Multiple Pheromone agents

reaching the same robot are combined into a single

agent. Their vector data are synthesized into a single

vector datum, and then stored into the single agent.

Although the previous approach yielded favorable

results for its efﬁciency and energy consumption in

the experiments, it just gathered robots, and did not

consider how to align them as shown by 4 of Figure

1. Consider applying the approach to carts in termi-

nals of the airport as mentioned above. After the carts

have been roughly gathered, the laborers would have

to take them away, for which they would serialize the

carts. Such serialization task would be still laborious

for the human workers even if the carts are roughly

gathered.

Recently, we proposed an approach not only gath-

ering robots but also serializing them (Shintani et al.,

2011). In the approach, a pheromone agent on a robot

in a cluster initially has a vector value indicating the

back of the robot. When several pheromone agents

migrate to the same robot, the Ant agent on the des-

tination robot picks up the one that comes from the

nearest robot, instead of combining them. Then the

Ant agent, while it is guided by the pheromone agent,

drives the robot, on which it resides, to the tail of

the nearest cluster. These extensions for the previ-

ous approach enable each cluster generated by dis-

tributed ACC to be serialized without sacriﬁcing su-

perior properties. They work quite well on a simula-

tor. However, every robot potentially holds the max-

imum number of Pheromone Agents, which can lead

to a fatal problem for robots with limited resources.

In this paper, we propose yet another algorithm to

serialize the robots in an assembled cluster. In this

algorithm, when several pheromone agents migrate

to the same robot, they are combined into a single

agent with a synthesized vector datum in the manner

where the vector value to a closer destination more

strongly affects the new vector value. These new ex-

tensions practically enable each cluster generated by

distributed ACC to be serialized without sacriﬁcing

superior properties.

The structure of the balance of this paper is as fol-

lows. In the second section, we describe the back-

ground. The third section describes basic properties

of Pheromone Agents. The fourth section describes

how the new algorithm performs the quasi optimal

clustering of the mobile robots and serializing them

based on Pheromone Agents. The ﬁfth section de-

scribes the numerical experiments using a simulator

based on our algorithm. Finally, we conclude in the

ﬁfth section and discuss future research directions.

2 BACKGROUND

Kambayashi and Takimoto have proposed a frame-

work for controlling intelligent multiple robots using

higher-order mobile agents (Kambayashi et al., 2009;

Kambayashi and Takimoto, 2005; Takimoto et al.,

2007). The framework helps users to construct intel-

ligent robot control software by migration of mobile

agents. Since the migrating agents are higher-order,

the control software can be hierarchically assembled

while they are running. Dynamically extending con-

trol software by the migration of mobile agents en-

ables them to make base control software relatively

simple, and to add functionalities one by one as they

know the working environment. Thus they do not

have to make the intelligent robot smart from the be-

ginning or make the robot learn by itself. They can

send intelligence later as new agents. Even though

they demonstrate the usefulness of the dynamic exten-

sion of the robot control software by using the higher-

order mobile agents, such higher-order property is not

necessary in our setting. We have employed a sim-

ple, non higher-order mobile agent system for our

framework. They have implemented a team of co-

operative search robots to show the effectiveness of

their framework, and demonstrated that their frame-

work contributes to energy saving of multiple robots

(Takimoto et al., 2007; Nagata et al., 2009). They

have achieved signiﬁcant saving of energy for search

robot applications.

On the other hand, algorithms that are inspired

by behaviors of social insects such as ants to com-

municate to each other by an indirect communication

called stigmergy are becoming popular (Dorigo et al.,

2006; Dorigo and Gambardella, 1996). Upon ob-

serving real ants’ behaviors, Dorigo et al. found that

ants exchanged information by laying down a trail of

SYNTHESIZING PHEROMONE AGENTS FOR SERIALIZATION IN THE DISTRIBUTED ANT COLONY

CLUSTERING

221

Figure 2: The outline of the serialization algorithm.

a chemical substance (called pheromone) that is fol-

lowed by other ants. They adopted this ant strategy,

known as ant colony optimization (ACO), to solve

various optimization problems such as the traveling

salesman problem (TSP) (Dorigo and Gambardella,

1996). Deneubourg has originally formulated the

biology inspired behavioral algorithm that simulates

the ant corps gathering and brood sorting behaviors

(Deneubourg et al., 1991). Wang and Zhang proposed

an ant inspired approach along this line of research

that sorts objects with multiple robots (Wang and

Zhang, 2004). Lumer has improved Deneubourg’s

model and proposed a new simulation model that is

called Ant Colony Clustering (Lumer and Faiesta,

1994). His method could cluster similar objects into

a few groups.

3 BASIC PROPERTIES OF A

PHEROMONE AGENT

In a new algorithm for serializing robots, an Ant agent

and a robot respectively corresponds to an ant and an

object of ACC. The Ant agent traverse robots through

repeating migrations to ﬁnd a free robot with no task,

as it does in the previous approach (Mizutani et al.,

2010; Oikawa et al., 2010). Once the Ant agent

ﬁnds a free robot A, it behaves along the following

steps. Here AA denotes Ant agent, and PA denotes

Pheromone agent:

1. If there is no PA on robot A, an AA makes the

robot move randomly as shown by 1 of Figure 2.

2. If robot A approaches another robot B during the

random movement, robot A locks itself next to

Figure 3: Calculating the vector value of PA migrating from

a locked robot.

robot B. They compose an initial cluster, as shown

by 2 of Figure 2.

3. If a PA migrates to robot A, the PA guides the

AA following its vector information indicating the

back of the robot C on which the PA was origi-

nally created as shown by 3 of Figure 2.

4. Once robot A reaches the tail of a cluster, the AA

make it turn to the head of the cluster as shown by

4 of Figure 2.

5. Robot A is locked there as a member of the cluster

as shown by 5 of Figure 2.

As soon as a robot is locked as a member of a

cluster, a new PA is created by AA on it and then the

PA migrates to other robots to attract more robots to

the cluster.

3.1 Diffusion

The vector datum of PA represents a vector that points

from the current robot to the destination. Here the

destination is the robot on which PA was created, i.e.

the cluster which PA was created. Therefore the vec-

tor points to the destination and its length represents

the distance to the destination.

The PA has initial vector value indicating the back

of the tail of a cluster, and it is expected to hold the

initial destination to guide AA to the cluster. How-

ever, each time the PA migrates to another robot to

make it diffuse, the vector value becomes pointing to

a location getting out of the initial point. In order to

make the current destination corresponds to the initial

one, the vector value has to be adjusted based on the

direction and the distance of each migration. This ad-

justment can be achieved by the Equation 1. Assume

here that PA migrates from a robot to another one.

Current vector value V

new

can be calculated based on

vector value V

on the source robot of the migration

and vector value V

indicating the source from the

destination of the migration as follows:

new

= V

(1)

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

222

The calculation is repeated every time the agent is mi-

grated to another robot.

Figure 3 shows relations of vector values in the

process where PA migrates from locked robot A to

robot C through B. The initial PA which is denoted as

PA1 has vector1 indicating the tail of the cluster it be-

longs. If PA1 migrate to robot B to diffuse, which is

denoted as PA2 after the migration, PA2 has the vec-

tor value vector3. As shown by Equation 1, it can be

calculated through vector1 + vector2, where vector2

is the vector value indicating the source of the mi-

gration. If PA2 with vector3 migrates to robot C fur-

ther, which is denoted as PA3 after the migration, PA3

has the vector value vector5, which is obtained from

vector3 +vector4 using vector4 indicating the source

of the second migration as well as the ﬁrst migration.

3.2 Synthesis

Let us consider a case where a PA migrates to another

robot, another PA has already existed on the robot. In

this case, it is proﬁtable for these PAs to be combined

into a single agent, because such a combination sim-

pliﬁes operations to PAs, and contributes to efﬁcient

use of CPU and memory resources. To achieve the

combination, the vector data of the PAs need to be

also synthesized into one vector datum. Notice here

that simple synthesizing of the vector values may not

lead to desirable result. Considering energy consump-

tion and efﬁciency of convergence of ACC, it is de-

sirable for an AA to be guided to the nearest cluster.

However the vector value that points to far distance

is dominant in the simple synthesized vector value as

shown by Figure 4.

We adopt harmonic mean in our synthesizing vec-

tor values. Harmonic mean has the property that it

is closer to the minimal value of all values, that is,

the harmonic mean of vector values is closer to the

vector value with the nearest destination. This is

what we desire. Thus, the vector value which results

from combining several PAs with vector value V

(i = 1, 2, ..., n) is calculated as follows:

new

+ ... +

(2)

4 PHEROMONE BASED

SERIALIZATION

We describe details of serializing a cluster based on

PA in this section. The serialization process consists

of two behaviors of PA; one is moving to the tail of

a cluster and the other is guiding AA along its vector

information.

Figure 4: Synthesizing of the vector values.

Figure 5: The property of moving behind.

4.1 Moving to the Tail

As shown by the operations to a vector datum of a PA,

whenever a PA migrates to outside of a cluster, the

PA has to always migrate from the tail of the cluster.

Otherwise, a PA may guide AA to the middle point

of a serialized cluster, generating some branches in

the cluster. We make PAs move to the tail of a clus-

ter as soon as they are created as shown by Figure 5.

The movement is composed of several migrations to

a robot behind a current robot. Notice that, in the pro-

cess of the movement, when a PA migrates to a robot

where another PA has already existed, a different op-

eration is required. In this case, the PA is just killed

instead of being combined. Because the PA on the

tail robot only has a vector value indicating the back

of it, thus the combination is unnecessary. Thus, it is

guaranteed that any clusters have only one PA at their

tails.

4.2 Guiding Ant Agents

When an AA migrates to a robot with no PA, the AA

drives the robot randomly to look for other robots.

Once an AA migrates to a robot with a PA or a PA mi-

grates to a robot with an AA, the AA drives the robot

along guidance of the PA. We call such a driving man-

ner Pheromone Walk. Figure 6 shows the process of

the Pheromone Walk. Each step is as follows:

SYNTHESIZING PHEROMONE AGENTS FOR SERIALIZATION IN THE DISTRIBUTED ANT COLONY

CLUSTERING

223

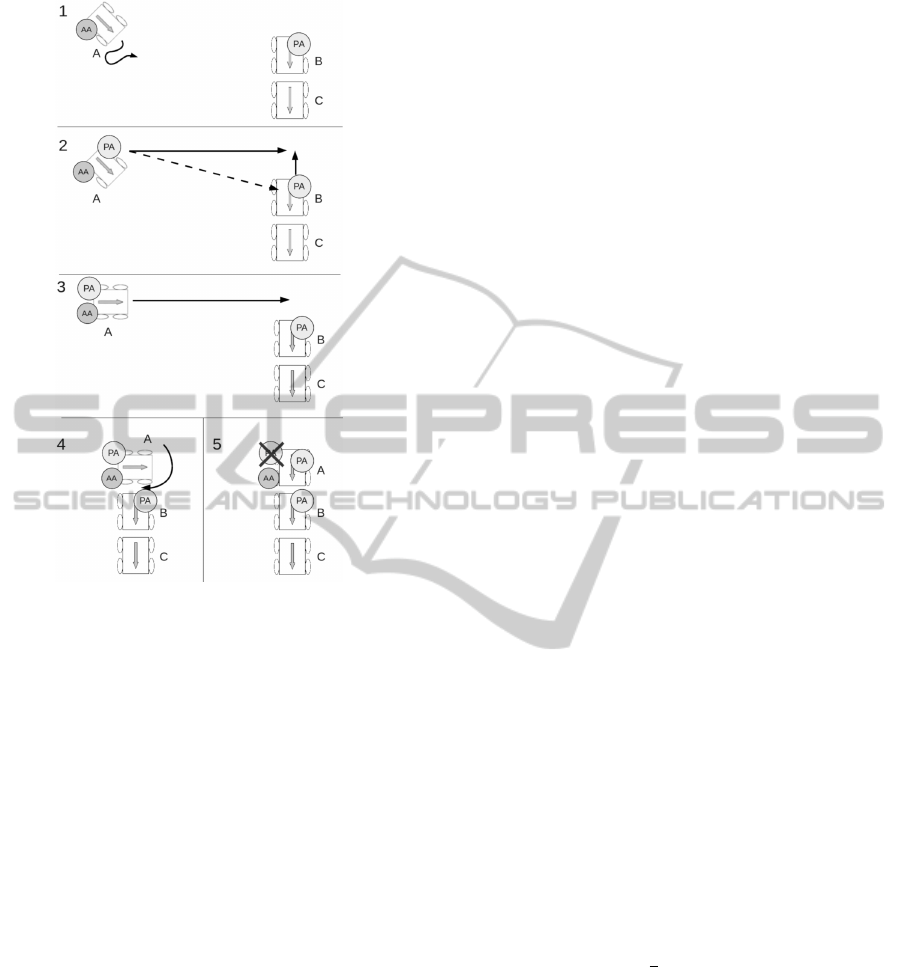
Figure 6: The process for moving to the tail of a cluster.

1. The AA on the robot A drives its robot randomly

and the robot happens to approach a cluster.

2. The PA on the robot B in the cluster migrates to

the robot A. The PA adjusts its vector datum be-

cause of keeping the destination.

3. The PA guides the AA on the same robot and the

AA drives the robot to the destination. The robot

A is not locked until it reaches the destination des-

ignated by the PA even if it approaches another

robot.

4. The robot A reaches the destination. The AA

turns the robot A to the direction of the head of

the cluster.

5. The AA locks the robot A, kills the previous PA,

and creates a new PA.

The condition for avoiding locking during the

Pheromone Walk in step 3 is needed for serialization

without any branch.

The robot A joins to the cluster through these

steps. After that, the AA migrates to some robots

around robot A to ﬁnd another free robot.

5 EXPERIMENTAL RESULTS

In order to demonstrate the effectiveness of our sys-

tem in a realistic environment, we have implemented

a simulator for serializing robots and conducted ex-

periments on it. On the simulator, moving and rotat-

ing speed of robots, and time lags required in agent

migration and object recognition are based on real

values in the previous experiments using PIONEER

3-DX with ERSP (Mizutani et al., 2010; Oikawa

et al., 2010; Nagata et al., 2009). In the experiments,

we set the following conditions:

1. Robots are scattered in a 500 × 500 square ﬁeld in

the simulator.

2. Their initial locations and angles are randomly de-

cided without overlapping.

3. Each robot is represented as a square on the grid

ﬁeld.

In the ﬁrst set of experiments, we have visualized

the results of the non-serializing approach and the

new approach, where two hundreds robots were scat-

tered in the ﬁeld, and the ﬁfty robots of them had AA.

Figure 7 and 8 show these arrangements respectively.

A gray square on the grid denotes one robot, and a

circle with the robot at its center shows a scope of its

PA. As shown in the ﬁgures, new approach has suc-

cessfully serialized robots while the non-serializing

approach has just formed various shaped clusters.

Next, in order to quantitatively discuss these ar-

rangements, we have measured the total length of

clusters and the angle variances of the clusters, where

the length of a cluster is the length of a diameter of

the minimal circle surrounding the cluster and the an-

gle variance of a cluster is the average of angles in the

cluster. As shown by Figure 9 and as expected, the

total length of the diameters for the new approach is

twice as long as previous one. We can observe that

the arrangement for the new approach is more line-

like than the previous one. The average of angles for

previous approach is about 1.5 radian as shown in Fig-

ure 10. That is about

. It means that each robot

of a cluster uniformly faces different direction. On

the other hand, the average of angles for the new ap-

proach is much closer to zero than the previous one.

As a result, most robots in a cluster are facing to the

same direction.

The second set of experiments, in order to check

whether the some good properties of the previous ap-

proach are preserved or not, we have conducted sev-

eral experiments with the different numbers of robots

and AAs, and compared their results. As shown in the

Figure 11, in the previous approach, the average size

of a cluster seem to be about 5 and 6 robots, regard-

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

224

Figure 7: The result screen of the previous algorithm.

Figure 8: The result screen of the new algorithm.

Figure 9: The total length

of clusters.

Figure 10: The angle vari-

ance in a cluster.

less the number of AAs and the robots in the ﬁeld. On

the other hand, in the new approach, the average size

of a cluster has been gradually increasing with the in-

crease of the number of all the robots. Thus, we can

observe that the new approach tends to generate larger

clusters. This is because of the property of the new

approach that PA makes a robot ignore other clusters

except the destination cluster. Considering applying

our approach to the arrangement of carts in the air-

Figure 11: The size of cluster.

Figure 12: The average time taken till convergence.

Figure 13: The total length of traces.

port terminal, it is favorable property that our new ap-

proach creates moderately large (long) clusters as the

experiments show.

Next, as shown in the Figure 12, in the new ap-

proach, we can observe that the time period till con-

vergence for 50 AAs is equal to the time period for

30 AAs though it is less than the time period for 10

AAs, as well as the previous approach. In addition to

that, as shown in the Figure 13, the less the number of

AAs is, the shorter the total length of traces of each

robot is. Since the shorter trace means less energy

consumption, these results demonstrate that the new

approach also has the beneﬁcial features in which the

energy consumption can be decreased on some levels

without sacriﬁcing efﬁciency. These results show that

the new approach inherits the good properties from

the previous approach.

SYNTHESIZING PHEROMONE AGENTS FOR SERIALIZATION IN THE DISTRIBUTED ANT COLONY

CLUSTERING

225

6 CONCLUSIONS

We proposed a serialization algorithm for mobile

robots using mobile agents with the distributed ACC.

We showed that the algorithm can achieve the seri-

alization of clustered robots, and the algorithm also

inherits the good features of the previous algorithm in

experiments on a simulation system.

On the other hand, we can observe that some lined

clusters bent because of avoiding jutting out of the

ﬁeld. We are improving the current algorithm to make

clusters slowly bent along the edge of the ﬁeld or

other clusters, while preventing the formed clusters

being too large.

REFERENCES

Deneubourg, J., Goss, S., Franks, N. R., Sendova-Franks,

A. B., Detrain, C., and Chreien, L. (1991). The dy-

namics of collective sorting: Robot-like ant and ant-

like robot. In Proceedings of the First Conference

on Simulation of Adaptive Behavior: From Animals

to Animats, pages 356–363. MIT Press.

Dorigo, M., Birattari, M., and T. St

utzle (2006). Ant colony

optimization–artiﬁcial ants as a computational intel-

ligence technique. IEEE Computational Intelligence

Magazine, 1(4):28–39.

Dorigo, M. and Gambardella, L. M. (1996). Ant colony sys-

tem: a cooperative learning approach to the traveling

salesman. IEEE Transaction on Evolutionary Compu-

tation, 1(1):53–66.

Kambayashi, Y. and Takimoto, M. (2005). Higher-order

mobile agents for controlling intelligent robots. Inter-

national Journal of Intelligent Information Technolo-

gies, 1(2):28–42.

Kambayashi, Y., Ugajin, M., Sato, O., Tsujimura, Y., Ya-

machi, H., Takimoto, M., and Yamamoto, H. (2009).

Integrating ant colony clustering to a multi-robot sys-

tem using mobile agents. Industrial Engineering and

Management Systems, 8(3):181–193.

Lumer, E. D. and Faiesta, B. (1994). Diversity and adap-

tation in populations of clustering ants, from animals

to animats 3. In Proceedings of the 3rd International

Conference on the Simulation of Adaptive Behavior,

pages 501–508. MIT Press.

Mizutani, M., Takimoto, M., and Kambayashi, Y. (2010).

Ant colony clustering using mobile agents as ants and

pheromone. In Proceedings of the Second Interna-

tional Conference on Applications of Intelligent Sys-

tems, pages 435–444. Lecture Notes in Computer Sci-

ence 5990, Springer-Verlag.

Nagata, T., Takimoto, M., and Kambayashi, Y. (2009). Sup-

pressing the total costs of executing tasks using mo-

bile agents. In Proceedings of the 42nd Hawaii Inter-

national Conference on System Sciences. IEEE Com-

puter Society CD-ROM.

Oikawa, R., Mizutani, M., Takimoto, M., and Kambayashi,

Y. (2010). Distributed ant colony clustering using

mobile agents and its effects. In Proceedings of

the 14th KES International Conference on Agent and

Multi-Agent Systems, pages 198–208. Lecture Notes

in Computer Science 6276, Springer-Verlag.

Shintani, M., Lee, S., Takimoto, M., and Kambayashi, Y.

(2011). A serialization algorithm for mobile robots

using mobile agents with distributed ant colony clus-

tering. In Proceedings of the 15th International Con-

ference on Knowledge-Based and Intelligent Informa-

tion and Engineering Systems, to appear.

Takimoto, M., Mizuno, M., Kurio, M., and Kambayashi, Y.

(2007). Saving energy consumption of multi-robots

using higher-order mobile agents. In Proceedings of

the ﬁrst KES International Symposium on Agent and

Multi-Agent Systems, pages 549–558. Lecture Notes

in Artiﬁcial Intelligence 4496, Springer-Verlag.

Wang, T. and Zhang, H. (2004). Collective sorting with

multi-robot. In Proceedings of the First IEEE In-

ternational Conference on Robotics and Biomimetics,

pages 716–720.

ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications

226