
MAGS
An Aco-based Model to Solve the Schedule Generation and Fleet Assignment
Integrated Problem
Daniel J. Caetano and Nicolau D. F. Gualda
Universidade de São Paulo, Escola Politécnica, Departamento de Engenharia de Transportes
Av. Professor Almeida Prado, Trav. 2, n
o
83, Cidade Universitária, CEP 05508-900, São Paulo, SP, Brazil
Keywords: Air transportation, Schedule generation, Fleet assignment, Metaheuristic, Ant system.
Abstract: Schedule Generation and Fleet Assignment problems usually are solved separately. The integrated solution
for both problems, although desirable, leads to large scale models of the NP-Hard class. This article presents
a mathematical formulation of this integrated problem along with a new heuristical approach, called MAGS,
based on the ACO metaheuristic. Both the exact solution and the one provided by MAGS are obtained and
compared for the case of a Brazilian airline. The results have shown the applicability of MAGS to real
world cases.
1 INTRODUCTION
This paper presents a heuristic model that
incorporates the Ant Colony Optimization
metaheuristic to solve schedule generation and fleet
assignment integrated problems, avoiding model
simplifications that limit its application to real world
problems (Caetano, 2011); (Caetano and Gualda,
2010); (Rabeanety et al., 2006).
Initially, a brief review of a linear programming
model is presented, followed by the Multiple Ant
Colony Group System heuristic (MAGS), based on
the traditional Ant Colony Optimization (Dorigo and
Stützle, 2004). Finally, a comparison between the
results obtained through the metaheuristic and the
optimal results obtained with the linear
programming model is presented, followed by the
conclusions of the study.
2 AIRLINE OPERATIONAL
PLANNING
The traditional approach to solving the fleet
assignment models are based on a space-time
network, where arrival or departure airports are
represented by nodes. There are two basic types of
arcs on this representation: flight leg arcs –
connecting nodes that represent different airports –
or waiting time arcs – connecting nodes that
represent different times at the same airport (Berge
and Hoperstead, 1993 apud Sherali et al., 2006);
(Hane et al. 1995).
These classical models assume that the flight
schedule is previously defined, with every flight
being covered. Traditionally, they do not include
operational restrictions at airports. To overcome
these limitations, it is necessary to define a more
comprehensive model. The model presented in this
paper is based on the concept of space-time
modelling (Berge and Hoperstead, 1993 apud
Sherali et al. 2006); (Hane et al. 1995), extended to
cope with landing and departure slots by the addition
of landing arcs that connect an arrival node to the
first viable departure node, as shown in Figure 1.
The fleet assignment model can be integrated to
schedule generation with the addition of a penalty
for non served demand and relaxing the cover
constraint so that not all flights must be assigned.
The following sets, parameters and decision
variables are defined to describe the model:
Sets
M: set of all markets, indexed by m; each market
defines a demand and a time window which limits
which flights can serve this demand.
N
f
: set of all nodes for aircraft f, indexed by i, j, o, d
or k, representing an airport at a specific time.
Nrd: set of nodes with departure restrictions.
227
J. Caetano D. and D. F. Gualda N..
MAGS - An Aco-based Model to Solve the Schedule Generation and Fleet Assignment Integrated Problem.
DOI: 10.5220/0003673502270232
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 227-232
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
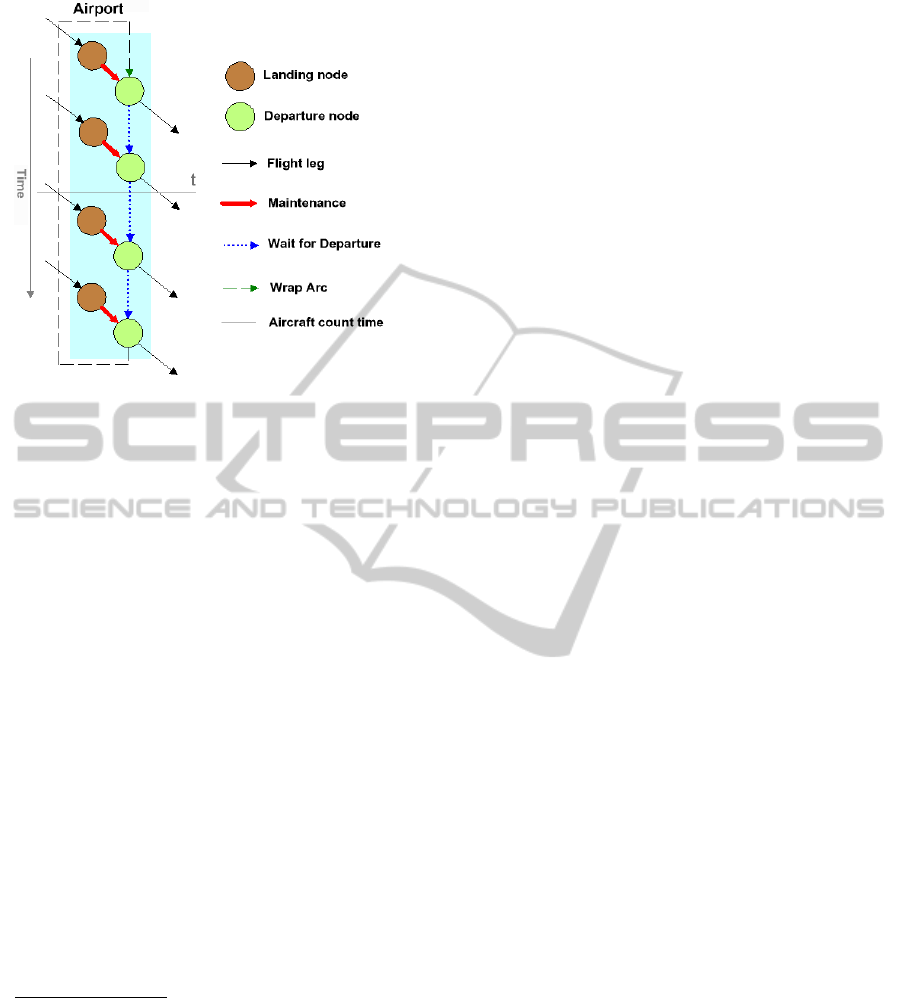
Figure 1: Space-Time Network.
Nra: set of nodes with landing restrictions.
F: set of all types of aircraft, indexed by f.
L: set of arcs that represent the movement of
aircraft, maintenance, waiting on the ground or
wrap, indexed by (i, j), being i the source node and j
the destination node of the movement.
Lv: set of arcs that represent flight movements.
Lvd: set of arcs representing flights assigned to a
market.
L
t
: set of arcs whose origin time is equal to or less
than t and destination time is after t. The time t is set
to a valid time according to the problem.
L
m
: set of arcs associated to market m.
Parameters
D
m
: unrestricted passenger demand on market m.
C
f
: number of seats of aircraft of type f.
R
ij
: unitary revenue for a passenger on the flight
from node i to node j. Since (i,j) represent an
specific flight – including day and time – each flight
may be associated with a specific unitary revenue.
A
f
: number of aircraft of type f available.
Decision Variables
x
f
ij
: number of aircraft of type f flowing through arc
(i, j).
pa
ij
: number of passengers associated to the flight
from node i to node j.
d
ij
: number of potential passengers (demand)
associated to the flight from node i to node j.
The objective function (expression 1) seeks to
minimize the sum of lost revenues. The first term
represents the difference between maximum revenue
for the assigned aircraft and the revenue received
from assigned passengers. The second term is
associated to the lost revenue due to lost demand.
(, )
[] .. .
.
{
[]
[] }
ff
ij ij ij ij
ij Lv f F
ij ij ij
Min R C x R pa
Rd pa
(1)
1 ( , )
f
ij
fF
x
ij Lvd
(2)
|( , ) |( , )
0 ,
ff
ok kd f
ook L d kd L
x
xkNfF
(3)
(, )
f
ij f
ij Lt
x
AfF
(4)
|( , )
1
f
id
fFdid Lv
x
iNrd
(5)
|( , )
1
f
oj
fFooj Lv
x
jNra
(6)
. 0 ( , )
ff
ij ij
fF
Cx pa ij Lv
(7)
0 ( , )
ij ij
dpa ijLv
(8)
(, )
0
ij m
ij Lm
dD mM
(9)
Binaries:
f
ij
x {0,1} for (i,j) Lvd
(10)
Integers:
f
ij
x 0 for (i,j) L\Lvd
(11)
ij
d 0 for (i,j) Lv
(12)
ij
p
a 0 for (i,j) Lv
(13)
Expressions 2 to 4 represent the traditional cover,
balance and number of aircraft restrictions (Berge
and Hoperstead, 1993 apud Sherali et al. 2006);
(Hane et al. 1995).
Expressions 5 and 6 represents slot constraints,
assuring that only one aircraft will depart or land on
those nodes, respectively. Expressions 7 to 9 assure
that each market demand will be associated to each
flight and that the passengers of a flight will never
be greater than the associated aircraft capacity.
The variables representing demanded flight arcs
are binary, and are specified on expression 10. All
other arc variables are integers greater than or equal
to zero, as stated on expression 11, 12 and 13.
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
228

3 ANT COLONY MODELING
Flight scheduling and fleet assignment are
traditionally solved using integer linear
programming techniques such as node clustering and
constraint relaxation. However, practical instances,
representing the operation of major airlines, remain
a challenge, given the computational complexity
involved. On the other hand, there are many
heuristics that are capable of finding very good
solutions to several types of combinatorial problems
(Rayward-Smith et al., 1996 apud Abrahão, 2005),
suggesting the search for heuristics that can provide
appropriate solutions for the problem in lower
processing times. The successful application to
problems like Vehicle Routing Problem (VRP) and
Aircraft Rotation Problem (ARP) draws attention to
the metaheuristic known as Ant Colony
Optimization (ACO), one of the many swarm
intelligence metaheuristics (Teodorovic, 2008).
3.1 ACO Applied to the Schedule
Generation and Fleet Assignment
Integrated Problem
Although it was possible to adapt the basic ACO
metaheuristic to solve the integrated flight schedule
and fleet assignment problem, the results obtained
through such approach were not satisfactory. Since
the basic ACO leads to a single shortest path, it must
be executed several times, assigning one aircraft at a
time and removing the selected arcs from the list,
leading to suboptimal solutions, with objective
function values almost three times the optimal ones.
However, the problem has specific
characteristics that can be used to improve the
overall solution and thus an alternative heuristic is
proposed, called Multiple Ant Group System
(MAGS), incorporating elements of Multiple Ant
Colony Optimization (MACO)(Vrancx and Nowé,
2006), Multiple Ant Colony System (MACS) and
Elitist Ant System (EAS)(Dorigo and Stützle, 2004),
as well as new elements not present on other ACO
metaheuristic variants.
3.2 Multiple Ant Group System –
MAGS Heuristic
MAGS is a multiple ant colony heuristic, such as
MACS and MACO. As in MACO, a solution is
represented by multiple ants; on the other hand, the
number of ants that build a specific solution is
previously known: there must be one ant per aircraft.
The ants that compose a solution are called an ant
group. A group may be composed of ants from
different colonies and, similar to what is presented in
MACS, each colony has a different objective
function. This means that ants from each colony
make decisions based on different criteria. In
MACS, however, pheromones are identical for all
colonies, which means it is substantially different
from MAGS.
The proposed solution construction process is
substantially different from the classical ACO, to
reduce the number of invalid and unrealistic
solutions. During the construction of a solution, the
ants of a group will alternately choose graph arcs.
The group’s ant which will take the next step is
randomly selected and whenever a flight arc is
associated to an ant, this arc will be no longer
available to other ants in the same group, ensuring
the construction of solutions in which two or more
aircraft do not share flights.
Additionally, when a flight is selected by an ant,
part of the flight’s market demand is also allocated,
reducing the demand available for other flights that
share the same market. This strategy avoids the
association of ants to flight arcs for which the
demand is no longer available in that solution. As
the demand for each arc becomes dynamic during
the construction of the solution, the problem
presents similar characteristics to the dynamic
routing in communication networks, as solved by the
AntNet heuristic (Dorigo and Stützle, 2004). The
exclusion of arcs and the demand allocation during
the solution construction have relevant effects on the
results, which are complementary to that provided
by the repellent pheromones proposed on MACO,
which continues to affect the selection probability of
each arc.
Considering the described construction process,
each ant group has the same role of a single ant in
the basic ACO: the group of ants represents the
complete objective function, each ant associated
with a different term of it. The MAGS basic logic is
presented in Figure 2.
As proposed by Dorigo and Stützle (2004), the
nearest neighborhood solution can be adopted as an
initial solution. On the addressed problem, the
"nearest neighbor" was defined as the arc associated
with the minimum revenue loss, avoiding waiting
arcs whenever possible. The objective function value
for this solution is used to determine the initial
pheromone deposit on each arc.
Differently from the basic ACO, the initial
pheromone deposit is not the same for all arcs. Arcs
associated with smaller heuristic values must receive
substantially more pheromones in the initial distri-
MAGS - An Aco-based Model to Solve the Schedule Generation and Fleet Assignment Integrated Problem
229

procedure MAGS
Setup Parameters
best=Nearest Neighborhood Solution
Setup Pheromones
for s Seasons
for g Ant Groups
Create Ant Group
sol=Build Ant Group Solution
sol=LocalSearch(sol)
if( sol < 1,05*best OR
sol > 2*best)
sol=LocalSearch2(sol)
if (sol < best) best=sol
end for g Ant Groups
Evaporate Pheromones
Update Pheromome trails
Update best AntGroup trail
end for s Seasons
end Procedure
Figure 2: MAGS basic logic.
bution than those associated to higher heuristic
values. Considering the basic ACO probability
equation (expression 14), an increased pheromone
deposit value on arcs that have low heuristic value
will also increase their likelihood of being chosen, at
least in the initial heuristic stage.
|( , )
.
.
i
ij ij
ij
il il
lil N
p
(14)
The probability equation adopted (expression 15),
however, presents some additional parameters. The
first one is
ij
, which represents the amount of
pheromone of other colonies, as in MACO, with
their respective coefficient . Additionally, the
parameter
ij
reduces the probability of selecting a
sequence of several unprofitable flights. The
ij
value is always 1.0 for profitable flight,
maintenance, and waiting arcs. For unprofitable
flight arcs, its value starts as 1.0 but upon the
addition of an unprofitable arc to the solution, the
value of
ij
is reduced by 50% for the next
unprofitable flight arc. This value is only reset to 1.0
when a profitable flight is selected to compose the
solution.
|( , )
1
.. .
1
.. .
i
ij ij ij
ij
ij
il il il
lil N
il
p
(15)
The
ij
value is proportional to the flight profit,
given that there is demand available in the market.
The
ij
is made equal to
ij
for repositioning flight
arcs – which have no markets associated to them –,
waiting arcs and maintenance arcs, since the
heuristic value based on lost revenue on these arcs
would be always non positive. The objective of this
measure is also to reduce the myopic heuristic
behavior, adding more emphasis on historical quality
of the solutions containing a specific arc, which is
represented by the pheromone deposit value.
After the initial pheromone is distributed, g ant
groups are generated, but no changes are made on
pheromones, as in the basic ACO. As the generation
of the ant groups is completed, pheromone
evaporation takes place, at a fixed rate, and then all
g ant groups will update their pheromone trails. As
in the EAS, the best solution will reinforce its own
pheromone trail, leading to convergence toward that
solution.
The pheromone deposit for each ant group is
proportional to the objective function value, as in the
basic ACO, but each ant of that group shall deposit
only part of the group total pheromone: the amount
of pheromone each ant of a group deposits is
proportional to the ant’s contribution to the quality
of the solution represented by that group. The
proposed distribution rule is defined by the
expression 16, where
f
is the deposit of each ant,
with
g
= 1/C
g
, where C
g
is the cost of the solution
represented by the group, calculated through the
objective function. R
f
is the revenue generated by
that ant and MR
g
is the maximum revenue that could
be generated by that group of ants.
.{0.5 [ / 2. ]}
fg f g
RMR
(16)
This formulation guarantees that each ant will
deposit a value not smaller than 50% of the deposit
calculated for the group and also ensures that it will
increase when the ant has a large contribution to the
group total revenue.
It is important to notice that when each group
finishes its solution construction, a local search is
performed to improve that solution. This local
search is divided into two steps: LS, which is
quicker and handles all the solutions, and LS2,
which is slower and processes only the solutions that
have a value close to the optimum one or are too far
from it. The LS is a procedure that removes
sequences of two unprofitable flight arcs. This
procedure also includes a corrective heuristic, which
adjusts the solution so that each ant’s terminal and
initial airports are the same. The LS2 supplements
LS, looking for profitable flights that could replace
waiting arcs on each ant’s path.
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
230

3.3 Application and Results
The mathematical model and MAGS were applied to
instances based on a domestic regional airline case
that carries 104 weekly flights and uses three ATR-
42/300 aircraft (for 50 passengers each). Alternative
flight networks were generated with different fleet
configurations, involving Embraer 120 (for 30
passengers each), and Embraer 170 (for 70
passengers each). Some of those instances also
include alternative flights for a new destination,
expanding the base network to 164 weekly flights,
plus thousands of potential repositioning flights with
no markets associated to them.
The demand distribution adopted on each
instance can be of three different types:
Fixed
: the demand associated to each flight is
fixed at 50 passengers.
Flight
: the demand is associated to each flight
and is the average demand per flight, based on
values provided by the Brazilian Civil Aviation
regulatory agency –
ANAC (2007).
Period
: the demand between two airports
associated to a period of day – morning or evening –
is the average demand by day period, based on
values provided by ANAC (2007).
The instances were solved by integer linear
programming techniques through Gurobi Optimizing
software version 3, on an Intel Core2 Quad
computer with 2GB of memory, using four
processing cores and 200GB of available virtual
memory. MAGS was implemented using Java SE
version 6, running on the same equipment while
using only one of the cores, since MAGS was not
implemented using parallel programming.
Table 1 shows the results obtained by both the
exact mathematical model and MAGS for some of
the instances, given a weekly schedule. The values
of the objective function represent the total lost
revenue and, thus, the lower the value, the better the
solution.
Analyzing the results, it is possible to notice that
MAGS leads to results very close to those obtained
by the exact model, with small standard deviations
and much smaller processing times – none of the
instances took more than an hour on each run. The
minimum values obtained, shown in Table 2, are
even closer to the optimal ones: while the average
values are distant by up to 6% of the optimum, the
minima are no more than 3% greater than the
optimum value for each case.
The average processing time per arc was of 0.04
seconds. The processing times, though not directly
linear to the number of arcs, are very low compared
to processing times of the mathematical model
solved with the Gurobi Optimizer, even without a
parallel implementation for MAGS.
Table 1: Exact model and MAGS average results.
Instance
Demand
Type
Fleets /
Aircraft
Arcs
Flight Arcs /
Repositioning Arcs
(Potential)
Exact Model MAGS (10 Runs Average)
O.F.
Value
Time(s)
O.F.
Value***
Std.Dev.
Avg. Time
(s)
1
Fixed 3 / 3 35.367 312 / 15.636 0 3 0 0 0
2
Fixed 4 / 4 35.367 312 / 15.636 92.200 3 92.200 0 430
3
Fixed 3 / 3 44.907 492 / 20.316 175.000 7 177.500 0 803
4
Flight 3 / 3 44.907 492 / 20.316 897.345 14 916.475 0 828
5
Flight 5 / 5 74.845 820 / 33.860 809.365 172.800* 855.192 23.398 1.386
6
Flight 3 / 5 44.907 492 / 20.316 809.365 14.249 843.317 8.468 1.108
7
Period 1 / 3 14.969 164 / 6.772 870.120 68 878.324 3.615 2.236
8
Period 2 / 3 29.938 328 / 13.544 814.150 78.133** 831.716 3.220 2.792
9
Period 3 / 5 29.938 328 / 13.544 788.550 172.800* 807.112 9.452 3.372
(*) Processing was interrupted after the 2-day time limit (172.800 seconds).
(**) Processing was interrupted due to insufficient memory (2GiB RAM + 200GiB harddisk virtual memory).
(***) Average values do not include the construtive heuristic results.
MAGS - An Aco-based Model to Solve the Schedule Generation and Fleet Assignment Integrated Problem
231

Table 2: MAGS minimum results.
Instance
MAGS (10 Runs Minimum)
Value* MAGS / Optimum
Avg.
Time (s)
1
0 100.0% 0
2
92.200 100.0% 430
3
177.500 101.4% 803
4
916.475 102.1% 828
5
832.135 102.8% 1.386
6
833.865 103.0% 1.108
7
875.470 100.6% 2.236
8
829.170 101.8% 2.792
9
801.030 101.6% 3.372
(*) Minimum values do not include the constructive heuristic
results.
4 CONCLUSIONS
This study presented and compared results of two
types of models to solve the flight schedule and the
fleet assignment problems in an integrated way.
Both models incorporate the same objective function
and constraints, including real world operational
restrictions such as slots at airports.
One of the models relies on Linear
Programming. The other, addressed to solve large
scale problems, a heuristic approach called MAGS –
Multiple Ant Group System – is based on the ACO
metaheurisic. MAGS presents a distinctive way to
determine the initial pheromone level on each arc, as
well as alternative rules for the construction of
solutions, each one being represented by multiple
ants. In addition, the multiple ant solution
representation required a new rule for pheromone
updating. The exact model could reach optimal
solutions for relatively small instances. MAGS has
reached very close results to the optimal ones in
smaller processing times, addressing the possibility
to utilize it to solve larger real world problems.
ACKNOWLEDGEMENTS
The authors acknowledge CAPES (Coordenação de
Aperfeiçoamento de Pessoal de Nível Superior) and
CNPq (Conselho Nacional de Desenvolvimento
Científico e Tecnológico) for financial support and
LPT/EPUSP (Laboratório de Planejamento e
Operação de Transportes da Escola Politécnica da
USP) for technical support.
REFERENCES
Abrahão, F.T.M., 2005. A Meta-Heurística Colônia de
Formigas para Solução do Problema de Programação
de Manutenção Preventiva de uma Frota de Veículos
com Múltiplas Restrições: Aplicação na Força Aérea
Brasileira. Thesis. Universidade de São Paulo. São
Paulo, Brazil.
ANAC, 2007. Anuário Estatístico da Agência Nacional de
Aviação Civil vol.I . Available at http://goo.gl/GJsba .
Accessed on 27/05/2011.
Caetano, D. J.; Gualda, N. D. F., 2010. A Flight Schedule
and Fleet Assignment Model. In: 12th World
Conference on Transport Research, Lisboa (Portugal).
Selected Procedures of the 12
th
WCTR (Paper ID:
02492). WCTRS, v. 1, p. 1-18.
Caetano, D. J., 2011. Modelagem Integrada para a
Programação de Voos e a Alocação de Frotas:
Abordagens Baseadas em Programação Linear Inteira
e na Meta-Heurística Colônia de Formigas. Thesis.
Universidade de São Paulo. São Paulo, Brazil.
Dorigo, M; Stützle, T., 2004. The Ant Colony
Optimization. Bradford Book, 2004.
Hane, C.; Barnhart, C.; Johnson, E.; Marsten, R.;
Nemhauser, G.; Sigismondi, G., 1995. A fleet
assignment problem: Solving a large-scale integer
program, Technical report, Georgia Institute of
Technology, School of Industrial and System
Engineering. Report Series 92-04.
Rabetanety, A.; Calmet, J.; Schoen, C., 2006. Airline
Schedule Planning Integrated Flight Schedule Design
and Product Line Design. Thesis. Universität
Karlsruhe. Karlsruhe.
Sherali, H. D.; Bish, E. K., Zhu, X., 2006. Airline fleet
assignment concepts, models, and algorithms,
European Journal of Operational Research , n.172,
p.1-30.
Teodorovic, D., 2008. Swarm Intelligence Systems for
Transport Engineering: Principles and Applications,
Transportation Research Part C: Emerging
Technologies, v.16, n.6, p.651-667.
Vrancx, P; Nowé, A., 2006. Using Pheromone Repulsion
to Find Disjoint Paths. In: Dorigo, M; Gambardella,
L.M; Birattari, M; Martinoli, A; POLI, R; Stützle, T.
(editors) Ant Colony Optimization and Swarm
Intelligence 5
th
International Workshop. ANTS 2006,
Brussels, Belgium – Procesdings. Belgium p.522-523.
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
232
