
IMPROVING THE PERFORMANCE OF THE SUPPORT
VECTOR MACHINE IN INSURANCE RISK CLASSIFICATION
A Comparitive Study
Mlungisi Duma, Bhekisipho Twala, Tshilidzi Marwala
Department of Electrical Engineering and the Built Environment, University of Johannesburg APK
Corner Kingsway and University Road, Auckland Park, Johannesburg, South Africa
Fulufhelo V. Nelwamondo
Council for Scientific and Industrial Research (CSIR), Pretoria, South Africa
Keywords: Support vector machine, Principal component analysis, Genetic algorithms, Artificial neural network,
Autoassociative network, Missing data.
Abstract: The support vector machine is a classification technique used in linear and non- linear complex problems. It
was shown that the performance of the technique decreases significantly in the presence of escalating
missing data in the insurance domain. Furthermore the resilience of the technique when the quality of the
data deteriorates is weak. When dealing with missing data, the support vector machine uses the mean-mode
strategy to replace missing values. In this paper, we propose the use of the autoassociative network and the
genetic algorithm as alternative strategies to help improve the classification performance as well as increase
the resilience of the technique. A comparative study is conducted to see which of the techniques helps the
support vector machine improve in performance and sustain resilience. The training data with completely
observable data is used to construct the support vector machine and testing data with missing values is used
to measuring the accuracy. The results show that both models help increase resilience with the
autoassociative network showing better overall performance improvement.
1 INTRODUCTION
Insurance industries have played a crucial role in
carrying risks on behalf of clients since their
inception in the late seventeenth century. These risks
include carrying the cost of a patient admitted to a
hospital, vehicle repairs for a client involved in a car
accident and many other incidents. However,
numerous people today still do not have an
insurance cover. The first well-known reason is
refusing to get a cover (Crump, 2009); (Howe,
2010). Many people believe that insurance
companies are there to make profits rather than
helping their clients. Therefore they would rather
save their money and incur the risk of paying the
cost if any catastrophic event happens to them
(Crump, 2009). The second common reason is
cancellation. Fraud, failing to pay premiums on time
or numerous claims results in client policies being
terminated by the insurer (Crump, 2009); (Howe,
2010). The third common reason is affordability
(Howe, 2010). The premiums for a cover may be
very expensive due to increasing premiums. A client
is therefore forced to cancel the cover.
In this paper, a solution to improve the support
vector machine (SVM) as a predictive modelling
technique in the insurance risk classification is
presented. The solution improves the manner in
which client risk is predicted using new data. The
model is trained using past data (with a large number
of features) about clients who are likely to have
insurance cover. This information is then used to
predict the future behaviour of a new client. The
new client data in this case, has attributes with
missing values. Missing values are due to clients
failing to supply the data, or processing error by the
system handling the data (Duma et al., 2010).
Support vector machines struggle with
classification performance compared to other
supervised algorithms (such as the naïve Bayes, k-
340
Duma M., Twala B., Marwala T. and V. Nelwamondo F..
IMPROVING THE PERFORMANCE OF THE SUPPORT VECTOR MACHINE IN INSURANCE RISK CLASSIFICATION - A Comparitive Study.
DOI: 10.5220/0003673803400346
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 340-346
ISBN: 978-989-8425-84-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

Nearest Neighbour, and the logical discriminant
algorithms) if new data contains missing data (Duma
et al., 2010). One of the main reasons is over-fitting
of the data. Even though support vector machines
are designed to be less prone to over-fitting, in very
high dimensional space, this problem cannot be
avoided. When training support vector machines, a
lot of detail is learned if the client data has many
attributes. The result of this is incorrect predictions
of new client data, especially if new data is of poor
quality as a result of missing values. The model also
has little resilience in the presence of increasing
missing data. In comparison with other supervised
learning models, its classification performance
decreased sharply when the quality of the data
deteriorated.
We present a comparative study on genetic
algorithms and autoassociative networks as effective
models to help improve the classification of the
support vector machines and increase resilience.
Genetic algorithms have been applied successfully
as methods for optimising classification algorithms,
(Chen et al., 2008); (Minaei-Bidgoli et al., 2004). It
has also been applied in fault classification of
mechanical systems as a method for estimating
missing values (Marwala et al., 2006).The
autoassociative networks have been applied
successfully in HIV classification (Leke et al.,
2006), missing data imputation (Marivate et al.,
2007) and assisting in image recognition (Pandit et
al., 2011).
We also employ the use of the principal
component analysis (PCA) as a feature selection
technique to reduce over-fitting and computational
cost. Principal component analysis removes those
dimensions that are not relevant for classification.
The reduced dataset in then passed on to the support
vector machine to learn. Principal component
analysis has been applied successfully in fault
identification and analysis of vibration data
(Marwala, 2001). Is has also been used in automatic
classification of ultra-sound liver images
(Balasubramanian et al., 2007) and in identifying
cancer molecular patterns in micro-array data (Han,
2010).
The rest of the paper is organised as follows:
Section 2 gives a background discussion on the
support vector machine, the principal component
analysis, genetic algorithms, autoassociative
networks and missing data mechanisms. Section 3 is
a discussion on the datasets and pre-processing. A
discussion on the AN-SVM structure and the GA-
SVM structure is also given. Section 4 is a
discussion on the experimental results. Conclusion
and future works is discussed in section 5.
2 BACKGROUND
2.1 Support Vector Machine
Support vector machine is a classification method
applied to both linear and non-linear complex
problems (Steeb, 2008). It makes use of a non-linear
mapping to transform data from lower to higher
dimensions. In the higher dimension, it searches for
an optimal hyper-plane that separates the attributes
of one class to another. If the data set is linearly
separable (i.e. a straight line can be drawn to
separate all attributes of a one class from all
attributes of another), the support vector machine
finds the maximal marginal hyper-plane, i.e. the
hyper-plane with the greatest margin. The separation
satisfies the following equation (Steeb, 2008),
(1)
where is the weight vector and is the input
vector. A larger margin allows classification of new
data to be more accurate. If the data set is linearly
inseparable, the original data is transformed into a
new higher dimension. In the new dimension, the
support vector machine searches for an optimal
hyper-plane that separates the attributes of the
classes. The maximal marginal hyper-plane found in
the new dimension corresponds to the non-linear
surface in the original space. The mapping of input
data into higher dimensions is performed by kernel
functions expressed in the form (Steeb, 2008),
(2)
where and are nonlinear mapping
functions. There are three commonly used kernel
functions used to training attributes into higher
dimensions, namely the polynomial, Gaussian radial
basis and sigmoid function (Steeb, 2008). In this
paper, we use the Gaussian radial basis function.
Support vector machines have been applied
successfully in the insurance industry
and in credit
risk analysis. They have been used to help identify
and manage credit risk (Chen et al, 2009, Yang et al,
2008). They have also been employed to predict
insolvency (Yang et al, 2008).
2.2 Principal Component Analysis
Principal component analysis (PCA) is a popular
IMPROVING THE PERFORMANCE OF THE SUPPORT VECTOR MACHINE IN INSURANCE RISK
CLASSIFICATION - A Comparitive Study
341

feature extraction technique used to find patterns in
data with many attributes and reduce the number of
attributes (Marwala, 2009).
In most instances, the goal of the principal
component analysis is to compress the dimensions of
the data whilst preserving as much as possible the
representation of the original data. The first step is
determining the average of each dimension and then
subtract from the values of the data. The covariance
matrix of the data set is then calculated. The eigen-
values and the eigen-vectors are determined using
the covariance matrix as a basis. At this point, any
vector dimension or its average can be expressed as
a linear combination of the eigenvectors. The last
step is choosing the highest eigen-values that
correspond to the largest eigenvectors, or the
principal components. The last step is where the
concept of data compression comes into effect. The
eigen-values that are chosen along with their
corresponding eigenvectors are used to reduce the
number of dimensions whilst preserving most
information (Marwala, 2009). This reduction can be
expressed as
[P] = [M] x [N] (3)
where [P] represents the transformed data set, [M]
represent the given data set and [N] is the principal
component matrix. [P] represents a dataset that
expresses the relationships between the data
regardless of whether the data has equal or lower
dimension. The original data set can be calculated
using the following equation
[M’] = [P] x [N
-1
] (4)
where [M’] represents the re-transformed data set
and [M’] ≈ [M] if all the data from [N
-1
] is used from
the covariance matrix.
2.3 Genetic Algorithm
Genetic algorithm (GA) is an evolutionary
computational model that is used to find global
solutions to complex problems (Michalewicz, 1996).
Genetic algorithms are inspired by Darwin’s theory
of natural evolution. They use the concept of
survival of the fittest over a number of generations
to find the optimal solution to a problem. In a
population, the fittest individuals are selected for
reproduction. The selection process is based on a
probabilistic technique that ensures that the strongest
individuals are chosen for reproduction. There are
various techniques that can be used for selection,
namely the roulette wheel selection, ranking
selector, tournament selection and stochastic
universal sampling (Michalewicz, 1996). The
roulette wheel selection uses a structure where each
individual has a roulette wheel slot size that is in
proportion to its fitness. The ranking selector orders
individuals according to their probability for
selection. The tournament selection technique
selects a random numbers of individuals, and then
assigns the highest probability to the fittest two
individuals. The stochastic universal sampling
technique is an alternative to the roulette wheel
selection. The technique ensures that the selection of
each individual is regular with its expected rate of
selection. In this paper, we use the roulette wheel
selection as it is a commonly used technique for
selection (Marwala, 2009).
After the selection process, steps involving
crossover, mutation and recombination are
performed to generate new individuals (Marwala,
2007, Steeb, 2008).
Crossover involves selecting a crossover point
between two parent individuals or chromosomes
(This can be a point in a string of bits or an array of
features that represent an instance in a dataset). Data
from the beginning of a chromosome to the
crossover point is exchange with another parent
chromosome. The results are two child
chromosomes. Mutation involves selecting a random
gene to invert it. It usually has a very low probability
of occurring than the crossover process (i.e. less than
1%). Recombination involves evaluating the fitness
value of the new individual to determine if they can
be recombined with the existing population. The
weakest individuals are removed from the
population (Marwala, 2007, Steeb, 2008).
2.4 Autoassociative Network
Autoassociative networks are specialized neural
networks that are designed to recall their inputs. This
implies that the input values supplied to the network
are the predicted output representing the inputs. The
number of hidden inputs in the hidden layer is often
less than the number of inputs. The number of
hidden layers cannot be too small otherwise the
learning results in poor generalisation and prediction
accuracy (Leke et al, 2006). In a classification
problem, the inputs vectors x ∈ℝ
include the
class value. The predicted values y∈ ℝ
are
expressed in the following form
=
(, )
(5)
where arethe mapping weights. The error function
e between the input vectors as well as the predicted
outputs, can be expressed in the form
NCTA 2011 - International Conference on Neural Computation Theory and Applications
342

=−
(6)
By squaring the error function and replaying with
equation (5) (Leke et al, 2006), we get
=(−
(, ))
(7)
we obtain the minimum and non-negative error,
which is what is required for the work presented in
this paper. Equation (7) can be expressed as a scalar
by integrating over the input vectors an the number
of training examples as follows
E =
‖
−
(, )
‖
(8)
where
‖‖
represents the Euclidean norm. The
minimum error is obtained when the outputs are the
closest matching to the inputs.
2.5 Missing Data Mechanisms
Information that is gathered from various sources
can have missing data. There are various reasons for
missing data. Some include people refusing to
disclose certain information for privacy or security
reasons, faulty processing by system and systems
exchanging information that has missing data
(Francis, 2005).
The mechanisms for handling missing data are
missing at random, missing completely at random,
missing not at random and missing by natural design
(Little et al, 1987, Marwala, 2009). Missing
complete at random infers that the missing data is
independent of any other existing data. Missing at
random infers that the missing data is not related to
the missing variables themselves but to other
variables. Missing not at random infers that the
missing data depends on itself and not on any other
variables. Missing by natural design infers that the
data is missing because the variable is naturally
deemed un-measurable, even though they are useful
for data analysis. Therefore, the missing values are
modelled using mathematical techniques (Marwala,
2009).
In this paper, we infer that the data is missing
completely at random. The reason is that single and
multiple imputations return unbiased estimates.
3 METHODS
3.1 Datasets and Pre-processing
There are two datasets used for conducting the
experiment. Both dataset are executed separately and
their results are combined. The first dataset is the
Texas insurance dataset used by the Texas
government to draw up the Texas Liability Insurance
Closed Claims Report. The report contains a
summary of medical insurance claims for various
injuries. The claims are either short form or long
form. Short form claims are associated with small
injuries that are not expensive for individuals to pay
for themselves. Long-term form claims are
associated with major injuries that are expensive and
require medical insurance. In this dataset, we
classify instances based on whether they have
medical insurance cover for long form claims as a
risk analysis exercise, provided there is missing
information.
The Texas Insurance dataset has over 9000
instances, which were reduced manually to 5446
instances by removing all the short form claims. The
dataset is separated into training and testing datasets,
1000 and 500 instances respectively (the datasets
were reduced to help increase the speed of the
training and testing processes. The instances were
also randomly chosen). Both sets have missing
values initially. We use the testing set to simulate
missing data. Each set consists of a total of over 220
attributes initially. The attributes were reduced
manually to 118 attributes by manually removing
those attributes that were not significant for the
experiment such as unique identities, dates etc. The
data was also processed to have categorical
numerical values for each attribute. The class
attribute used also has two values (0 to indicate no
medical insurance and 1 to indicate that the claimer
has medical insurance).
The second insurance dataset is from the
University of California Irvine (UCI) machine
learning repository. The dataset is used to predict
which customers are likely to have an interest in
buying a caravan insurance policy. In this paper, we
use it to find out customers who are likely to have a
car insurance policy for their motor vehicles,
provided there is missing data in the information
The training dataset has over 5400 instances of
which 1000 were used for the experiment. The
testing dataset consists of only 4000 instances of
which 800 instances were randomly chosen and
used. Analogous to the Texas Insurance dataset, the
subsets of the UCI training and testing datasets are
used so that the experiment runs at optimum speed.
Each set has a total of 86 attributes with completely
observable data, 5 of which are categorical numeric
values and 80 are continuous numeric values.
Processing was done to make the data consist of
categorical numeric values. The class attribute
consists of only two values (0 to indicate a customer
IMPROVING THE PERFORMANCE OF THE SUPPORT VECTOR MACHINE IN INSURANCE RISK
CLASSIFICATION - A Comparitive Study
343

that is likely not to have insurance or 1 to indicate a
customer that is likely to have an insurance cover).
There are five levels of proportions of
missingness on the testing datasets that are generated
(10%, 25%, 30%, 40% and 50% respectively). At
each level, the missingness is arbitrarily generated
across the entire datasets, then on half the attributes
of the sets. Therefore, in total, 30 testing datasets
were created for the experiment.
3.2 AN-SVM Structure
Figure 1 shows the structure for improving the
support vector machine using the autoassociative
network. We refer to the structure as the AN-SVM
structure. The initial step is compressing the data
using the principal component technique. The
compressed data is used to construct the
autoassociative network. Once the network is
constructed, it is used to select the best candidate for
the support vector machine to classify. A group of
candidates is created for each instance that has
missing values from the testing data. This is done by
randomly replacing missing entries with values for
each candidate. We create between 10 and 500
candidates for each instance, depending on the
number of missing values. The candidate with the
smallest error according to equation (8) is chosen for
classification. This is done until all instances that
have missing values have a potential candidate.
Figure 1: AN-SVM structure.
The autoassociative network is made up of the
input, hidden and output layers. There are 20 nodes
on hidden layer, determined by trial and error. The
Gaussian function is used as an activation function
between the input and hidden layer. The linear
activation function is used between the hidden and
output layer (Leke et al, 2006). The back-
propagation technique is used for learning and the
number of epochs is 400. The network is written
using C# 3.5 programming language, Weka and
IKVM libraries. The support vector machine is
constructed using Weka 3.6.2 and libSVM 2.91, a
library for tool support vector machines. The radial
basis function was used as the kernel function. The
principal component was also built using the Weka
3.6.2 library.
3.3 GA-SVM Structure
Figure 2 illustrates the genetic algorithm approach to
improving the support vector machine classification
performance. We refer to the structure as the GA-
SVM structure. The initial step is synonymous to the
AN-Structure. The only difference is that the genetic
algorithm is responsible for creating a population of
candidates and selecting the best one for
classification. Each candidate represents a potential
solution, i.e. it can belong to the 0 class or the 1
class. The maximum number of potential candidates
created is 15 for each instance with missing values.
Each candidate is represented as follows:
• Each observable entry is ignored, as illustrated by
the star (*) in figure 3. The other entries contain
generated values used to replace the missing values.
• During the crossover step, only the generated
values are exchanged to generate new individual.
Similarly, mutation step only occurs on entries with
generated values.
Each child candidate’s fitness is evaluated using
equation (8). The roulette wheel selection is used in
the selection step. The genetic algorithm is
constructed using the watch-maker framework 0.7.1.
The number of epochs is 100 and the mutation
probability was 0.0333, as recommended by Leke
(Leke et al, 2006) and Marwala (Marwala et al,
2006).
Figure 2: GA-SVM structure.
NCTA 2011 - International Conference on Neural Computation Theory and Applications
344

Figure 3: Candidate representation. * means ignored
entries. X
1
…X
n
are attributes and C
1
is the class-label.
4 EXPERIMENT RESULTS
The overall results of the experiment are illustrated
in table 1. The AN-SVM and the GA-SVM are
compared with MODE-SVM, support vector
machine that uses the mean-mode strategy to replace
missing values. All the models perform well overall
with AN-SVM achieving higher accuracies than the
other models by a small margin. The GA-SVM
achieves a lower accuracy than the MODE-SVM.
The reason being is that the MODE-SVM achieves
high accuracies when there is a small percentage of
missing data. Furthermore the GA-SVM struggled
with performance when data was missing across all
attributes compared to other models. This is
illustrated in figure 5.
Table 1: Overall Classification Accuracy.
Accuracy (%)
MODE-SVM 89.94
AN-SVM 90.04
GA-SVM 89.145
The overall performance in figure 4 shows that
the AN-SVM and GA-SVM are more resilient to
escalating missing data than the MODE-SVM. From
figure, the performance of the MODE-SVM
decreases sharply as the quality of the data
deteriorates. The AN-SVM shows more steadiness
in declining performance than the other models.
Figure 6 shows the overall performance of the
models with half or all attributes with missing data.
From the figure, it is clear that all the models
perform well and show more resilience when there is
half the attributes with missing value. In the case
when all or most attributes have missing data, a
sharp decline in performance is experienced when
the percentage of missingness increase above 30%.
The Mode-SVM contributes mostly in the sharp
decrease.
5 CONCLUSIONS AND FUTURE
WORK
We conducted a study using the autoassociative
network and genetic algorithm to help improve the
classification performance of support vector
machines, in the presence of escalating missing data.
Although support vector machines perform well
when using the mean mode technique, the
performance declines sharply when the quality of the
data deteriorates. The autoassociative network
showed better performance than the genetic
algorithm. It also showed better resilience when the
percentage of missing data increased. The genetic
algorithm also showed some resilience.
Future work should focus on improving the
performance of the genetic algorithm by optimizing
the process illustrated in figure 2. The number of
candidates currently chosen is a few and a better
evaluation function can be used.
Figure 4: The overall performance of the MODE-SVM,
AN-SVM and GA-SVM.
Figure 5: Overall performance per model. Matt(all) is
short for most attributes with missing values. Matt(half) is
short for half the attributes with missing values.
IMPROVING THE PERFORMANCE OF THE SUPPORT VECTOR MACHINE IN INSURANCE RISK
CLASSIFICATION - A Comparitive Study
345
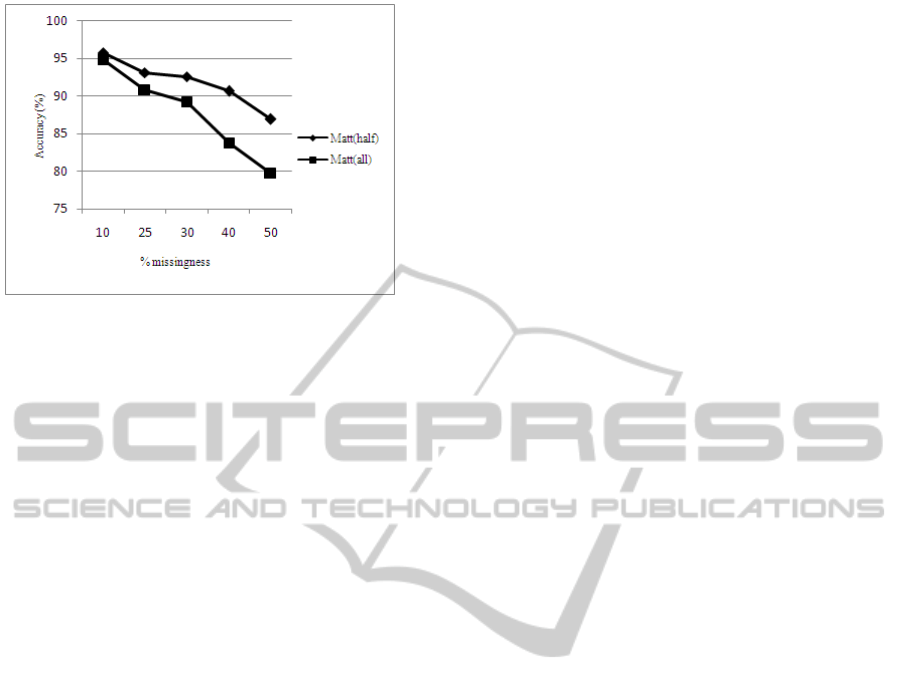
Figure 6: Overall performance with half or all attributes
with missing values. Matt(all) is short for most attributes
with missing values. Matt(half) is short for half the
attributes with missing values.
REFERENCES
Balasubramanian, D., Srinivasan, P., Gurupatham, R.,
2007. Automatic Classification of Focal Lesions in
Ultrasound Liver Images using Principal Component
Analysis and Neural Networks. In AICIE’07, 29th
Annual International Conference of the IEEE EMBS,
pp. 2134 – 2137, Lyon, France.
Bishop, C. M., 1995.Neural Network for Pattern
Recognition. Oxford University Press, New York,
USA.
Chen, M., Zhengwei, Y., 2008. Classification Techniques
of Neural Networks Using Improved Genetic
Algorithms. In ICGEC’08, 2
nd
International
Conference on Genetic and Evolutionary Computing,
pp.115 – 199, IEEE Computer Society, Washington,
DC, USA.
Crump, D., 2009. Why People Don’t Buy Insurance.
Ezine Articles. (Source: http://ezinearticles.com/
?cat=Insurance).
Duma, M., Twala, B., Marwala, T., Nelwamondo, F. V.,
2010. Classification Performance Measure Using
Missing Insurance Data: A Comparison Between
Supervised Learning Models. In ICCCI’10
International Conference on Computer and
Computational Intelligence, pp. 550 - 555, Nanning,
China.
Francis, L., 2005. Dancing With Dirty Data: Methods for
Exploring and Cleaning Data. Casualty Actuarial
Society Forum Casualty Actuarial Society, pp. 198-
254, Virgina, USA. (Source:http://www.casact.org/
pubs/forum/05wforum/05wf198.pdf)
Howe,C., 2010. Top Reasons Auto Insurance Companies
DropPeople.eHow. (Source:http://www.ehow.com/fact
s_6141822_top- insurance-companiesdrop-people.
html).
Leke, B., B., Marwala T., Tettey T., 2006. Autoencoder
Networks for HIV Classification. Current Science,
vol. 91, no. 11.
Little, R., J., A., Rubin, D., B., 1987. Statistical Analysis
with Missing Data. Wiley New York, USA.
Marwala T., 2001. Fault Identification using neural
network and vibration data. Unpublished doctoral
thesis, University of Cambridge, Cambridge.
Marwala, T., Chakraverty, S., 2006. Fault Classification in
Structures with Incomplete Measured Data using
Autoassociative Neural Networks and Genetic
Algorithm. Current Science, vol. 90, no. 4.
Marwala, T., 2007. Bayesian Training of Neural Networks
using Genetic Programming.
Marwala, T., 2009. Computational Intelligence for
Missing Data Imputation Estimation and Management
Knowledge Optimization Techniques, Information
Science Reference, Hershey, New York, USA.
Marivate, V., N., Nelwamodo, F., V., Marwala, T., 2007.
Autoencoder, Principal Component Analysis and
Support Vector Regression for Data Imputation.
CoRR.
Michalewicz, Z., 1996. Genetic algorithms + data
structures = evolution programs. Springer-Verlag,
New York, USA.
Minaei-Bidgoli, B., Kortemeyer, G., Punch W., F., 2004.
Optimizing Classification Ensembles via a Genetic
Algorithm for a Web-based Educational System.
Lecture Notes in Computer Science, vol. 3138, pp.
397-406.
Pandit, M., Gupta, M., 2011. Image Recognition With the
Help of Auto-Associative Neural Network.
International Journal of Computer Science and
Security, vol. 5, no. 1.
Steeb, W-H., 2008. The Nonlinear Workbook – 4th Edition
World Scientific, Singapore.
NCTA 2011 - International Conference on Neural Computation Theory and Applications
346
