
MODELLING A FUZZY SYSTEM FOR TEACHERS’ TRAINING
DESIGN
Eliza Stefanova
1
and Svetla Boytcheva
2
1
Faculty of Mathematics and Informatics, Sofia University, St. Kl. Ohridski, 5, James Bourchier, 1164 Sofia, Bulgaria
2
Department of Computer Science, State University of Library Studies and Information Technologies
119, Tzarigradsko Shosse, 1784 Sofia, Bulgaria
Keywords: Adaptive teachers training design, Fuzzy logic, Design of fuzzy controller.
Abstract: This paper presents a model, based on fuzzy logic, aiming to support teachers’ training design. The
complexity of the task of technology utilisation in education, leads the authors to decision to base its
adaptive system on fuzzy controller. We shortly describe the system architecture and its functionality. The
presentation includes also fuzzy model implemented in the kernel of the system, its components, linguistic
variables and values. Further steps for improvement of the system performance are sketched as well.
1 INTRODUCTION
Many researchers and politicians hope that
Information and Communication Technologies
(ICT) itself will dramatically change the education.
But it seems just ICT to be present in the schools is
not enough. They are not effectively used, in some
cases not used at all. One of the conclusions of the
Institute of Prospective Technological Studies report
(Cachia et al., 2010) is “it is necessary teachers to
be trained appropriately in order to have effective
use of technology in the school”. Although in many
countries massive teachers training on ICT were
done in recent years (Bulgaria, Romania, etc.), in
other (UK) - teacher professional development is
embedded in the systems, the expected changes still
are not visible. One of the reasons for
ineffectiveness is related to the design for teachers
training in field of integration of technology in
education. In this paper we will focus on the
problem and will discuss some possible solutions.
Teacher training is one of the four forms of the
professional development. In-service courses format
is appropriate and very effective when some
innovations are introduced and small number of
people are well informed about them (Guskey,
2010). Exactly this is the case with teachers training
in field of integration of technology across curricula.
Designing training, the characteristics of
professional developments of adult should be kept in
mind. It is not enough to build the knowledge for a
technology per se. The knowledge about technology
is context-dependable. The effective teaching of
technology requires an understanding how
technology relates to the pedagogy and content. As
consequence, the designers of teachers training
should aim to build Technological Pedagogical
Subject Knowledge (Mishra and Koehler, 2006).
More over, it is crucial to respect personal models
because personal values (as expressions of personal
priorities and positions) are inextricable from
making decisions by training designers (Pratt et al.,
in press). The characteristics of teachers training,
which design we would like to support, makes the
model very complex. In addition, the model should
be adaptable to different technologies, users and
their objectives.
In Section 1 we argue our decision to choose the
fuzzy logic as base of the approach to cope with the
problems. Second section is devoted to the design of
fuzzy logic controller. Finally, the aggregation done
by the system is presented. The conclusion sketches
some further steps in the research and the
improvement of the system prototype as well as
possible future use of the model and system itself.
2 FUZZY SYSTEM DESIGN
The field, we try to model, is too complex. The
505
Stefanova E. and Boytcheva S..
MODELLING A FUZZY SYSTEM FOR TEACHERS’ TRAINING DESIGN.
DOI: 10.5220/0003674505050508
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 505-508
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
formal modelling in similar cases is appropriate to
be developed through Fuzzy Logic (Zadeh, 1965;
Zadeh, 1973) integrated in Expert System. Such
model promises to support successfully designers of
training. We start the design of the model from
‘catching’ reality in the education: collecting
experts’ knowledge, converting it into the
conceptual abstract model, deriving the conclusions
based model and using it to support designers.
2.1 Components Identification
The identification of the components is based on
collecting experts’ understanding on importance of
the factors related to teachers training in digital
technologies for education. There were chosen
mainly components that affect to great degree
effective use of ICT in their school practice.
In this phase 23 experts from Bulgaria was
involved. Fifteen experts were most active
participants. They are experts in field of training
teachers for effective integration of ICT in
education.
Methodology used to collect experts opinion
follows the structured participative approach called
Group Concept Mapping, applied successfully in
solving similar problems (Stoyanov and Kirschner,
2004; Trochim, 1989; Wopereis et al., 2005). The
approach is very powerful combining both
qualitative and quantitative methods, but it is useless
without expert ideas and opinions. The Group
Concept Mapping procedure consists of four steps.
At first step the experts were asked to brainstorm
which are most important factor during the teachers
training, reflecting on effective use of the ICT in
school practice. Then, they send back the generated
by them list. The lists were collected and joint.
During the second step the list of all generated
factors was sent to the experts. They were asked: to
group the factors; to rank factors into each group
(according to their importance to relation with future
effective application of ICT in teachers practice); to
name the groups; to rank the groups (according to
their importance to relation with future effective
application of ICT in teachers practice).
After detailed analysis of the focus group
brainstorming, sorting and rating main components
of the model, a triangulation with parallel analysis
with two experts was then made. Four top factors,
rated by participants, are concluded to be main
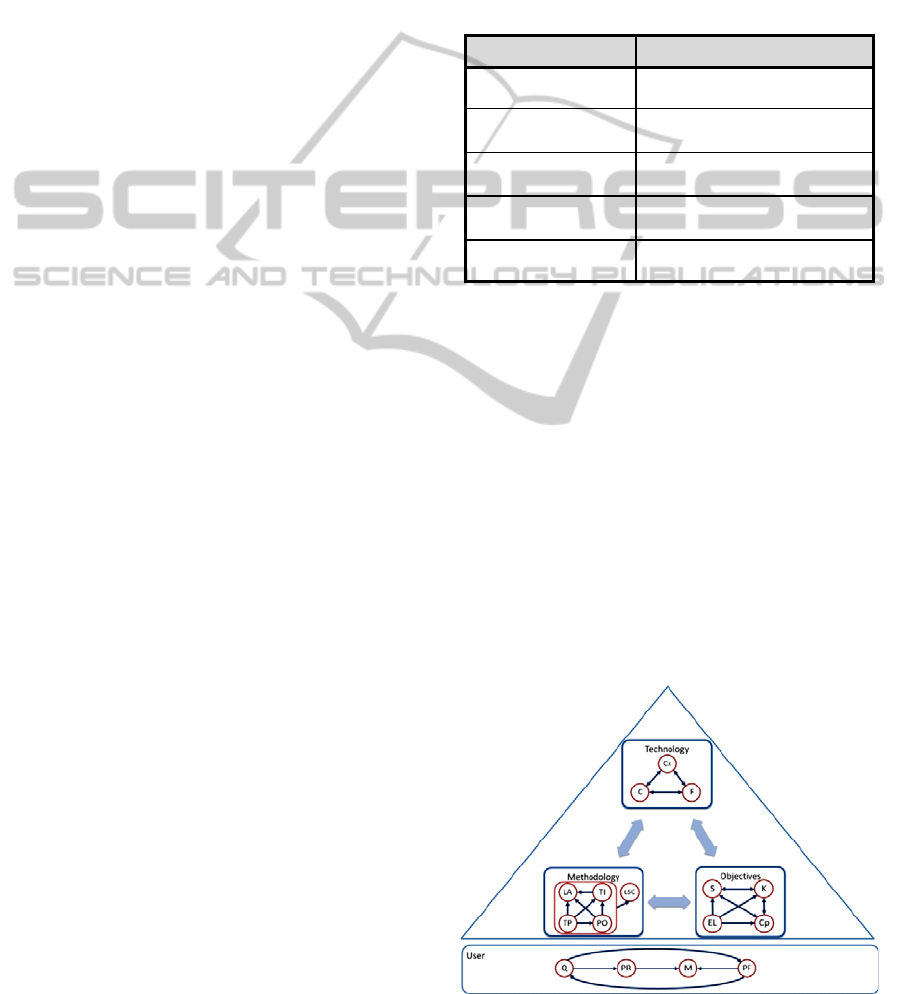
components of the model namely: Methodology,
Technology, User, Objectives.
2.2 Defining Linguistic Variable
The participants of Group Concept Mapping listed
main properties related with each of the factors
detected as important characteristic of the
component. On their base variables of each
component are created (Stefanova and Boytcheva,
2010). Table 1 presents methodology component
linguistic variables and values.
Table 1: Methodology linguistic variables and values.
Variable Values
Learner activity (LA)
Very Low, Low, Average, High,
Very High
Learners style
correspondence (LSC)
Fully, Almost, Slightly, None
Practice orientation
(PO)
Very Low, Low, Average, High,
Very High
Technology
Integration (TI)
Fully, Almost, Slightly, None
Technology present
(TP)
Very Abstract, Abstract,
Concrete, Very Concrete
The Objectives component has linguistic
variables Skills (S), Knowledge (K), Competence
(Cp) and Educational Level (EL). The User
component has following variables: Qualification
(Q), Motivation (M), Personal Reasons (PR), and
Professional Factors (PF). The Technology
component variables are Complexity (Cx), Cost (C),
Functionality (F), and Utilization (TU). Our main
goal is to make an inference about Technology
Utilization variable, based on the model and rules.
2.3 Defining Rules
The relations between components and their
linguistic variables are defined on based on experts’
opinion. They are presented on Figure 1.
Figure 1: Relations between linguistic variables.
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
506
In order to make the inference about technology
utilization it is necessary to choose in advance the
components priorities: how the user orders by
importance the component in the design of training.
Thus we can have methodology, technology or
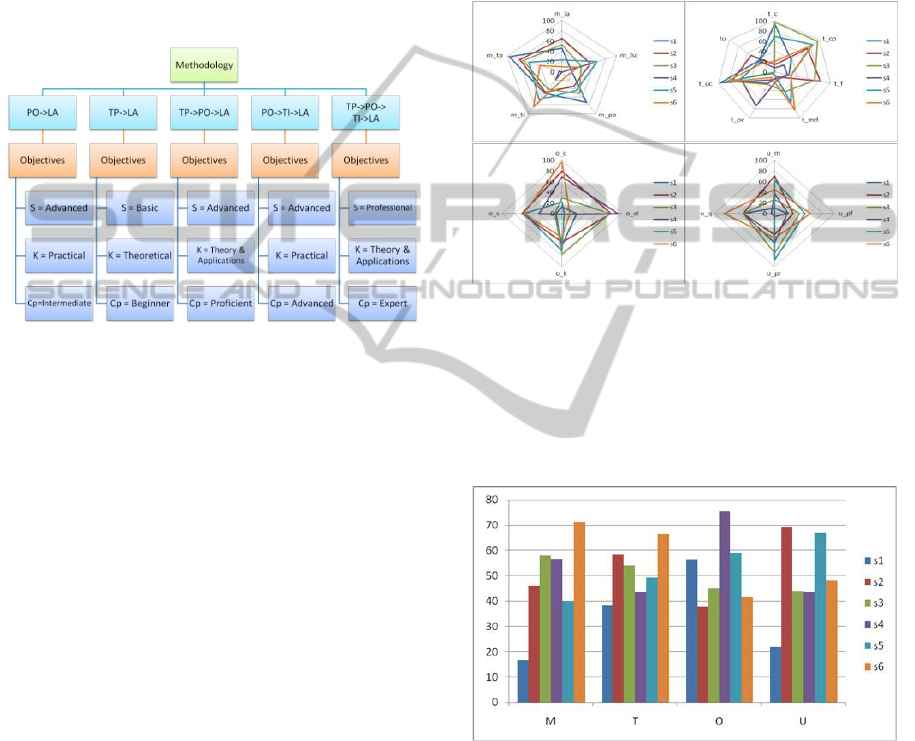
objective centred training approaches. On the Figure
2 the methodology centred approach dependences
are presented. In this case for different combinations
of the linguistic variables values for Methodology
component we can infer different combinations of
values for Objectives component.
Figure 2: Methodology Centric Approach: Inferred values
for Objectives.
On such base rules were generated using
Methodology variables values combinations for
prerequisites and setting values for objective
component variables as conclusion. However most
of the rules use not only single component variables
as prerequisites. About 75 rules were developed by
experts in the current stage of the project.
Triangular versions membership functions were
used to represent variables values. In inference
engine centroid technique is used.
3 AGGREGATION OF TRAINING
DESIGN MODELS
The designed model is used to build the fuzzy
system (Stefanova and Boytcheva, 2011) supporting
design of training models. One of its important
functionality is to compare users’ profiles in the
training group. This task can’t be performed as a
simple production of average values, due different
Training models and complex interrelations between
linguistic variables. The comparison procedure
includes usage of priorities for different linguistic
variables. These priorities are defined explicitly and
implicitly. The explicit priorities are settled during
the user registration in his/her profile, choosing
preferences for training method – methodology,
technology or objective centred. The implicit
priorities are based on user’s performance history.
Depending on linguistic variables priorities we
associate to each linguistic variable corresponding
weight.
We are comparing separately values of each
component Methodology, Technology, User,
Objectives (Figure 3).
Figure 3: Distances between values of linguistic variables
for each of the components of the model for six training
design models.
The comparison of multiple users’ models is quite
complex task. That is why we are comparing rather
individual values than the sum effect of them,
because the data are too disperses (Figure 4).
Figure 4: Comparison betwen total vatiables for each
component for six training design models.
Using the weight for each different variable in the
component we are calculating the total value of each
component. For instance for methodology we have
equation (1).
iiiiii
tpmwtimwpomwlscmwlamwM _._._._._.
54321
++++=
(1)
Similarly we calculate the total effect of
Technology (T), Objectives (O) and User (U). Then
we find the average values of totals for each
MODELLING A FUZZY SYSTEM FOR TEACHERS' TRAINING DESIGN
507

component and the deviations for Training design
models from it (2) and (3).
n
M
M
n
i
i
avg
∑
=
=
0
(2)
iavg
d
i
MMM −=
(3)
The final evaluation of models is the sum of
deviations of each model totals from the average (4).
d
i
d
i
d
i
d
i
d
i
UOTME +++=
(4)
Setting in advance the thresholds (t) the final
scores for two models E
i
and E
j
are considered the
same if their difference is bellow threshold.
tEE
d
j
d
i
<− ||
(5)
The final result of comparison of multiple user
training design models is clustered of similar models
depending on thresholds neighbourhood (Figure 5).
There are two cases:
One of the clusters dominates – in this case we
choose its aggregated training model for the
whole learning group.
None of the clusters is dominant – then we split
the group on subgroups corresponding to
clusters and perform aggregated training model
for each cluster individually.
Figure 5: Clustered space to four training design models.
4 CONCLUSIONS
In this paper we present work in progress. On the
current stage of the project we need to tune the
linguistic variables values and to test different
membership functions and inference engine
techniques for generating output values. The final
decision which of them fits best to our domain
representation would be made on the testing results
base. Further research steps will be followed by
testing and validating the model with available data
for already passed teachers’ trainings. On the results
base, the model will be refined. In order to approve
the proposed approach applicability into practice, the
prototype of the build fuzzy system will be tested
with teachers and instructional designers of teachers’
trainings.
REFERENCES
Cachia, R., Ferrari, A., Ala-Mutka K., Punie Y., 2010.
Creative Learning and Innovative Teaching: Final
Report on the Study on Creativity and Innovation in
Education in EU Member States, http://ftp.jrc.es/
EURdoc/JRC62370.pdf, Institute for Prospective
Technological Studies, last visited 27/05/2011.
Guskey, T. R., 2010. Evaluating Professional
Development, Corwin Press
Mishra, P., Koehler J. M, 2006. Technological
Pedagogical Content Knowledge: A Framework for
Teacher Knowledge, Teachers College Record,
Volume 108, Number 6, June 2006, pp. 1017–1054
Pratt, D., Ainley, J., Kent, P., Levinson, R., Yogui, C., and
Kapadia, R. (in press). Informal inferential reasoning
as a contextualised risk-based enterprise. To appear in
Mathematical Thinking and Learning
Stefanova E., Boytcheva S., 2010. Theoretical Framework
of Open Virtual Worlds for Professional Development,
In proceeding of S3T’2010 conference, Varna,
Bulgaria, 11-12 September 2010, pp.79-83
Stefanova E., Boytcheva S., 2011. Teachers’ Training
Design Model and Decision Support System, Springer
proceeding of S3T’2011 conference, Burgas, Bulgaria,
1-3 September 2011, pp.192-196
Stoyanov, S. & Kirschner, P. A., 2004. Expert concept
mapping method for defining the characteristics of
adaptive e-learning: ALFANET project case.
Educational Technology Research and Development,
52, 2, 41–56
Trochim, W., 1989. An introduction to concept mapping
for planning and evaluation, Evaluation and Program
Planning 12, 1–16
Wopereis, I., Kirschner, P. A., Paas, F., Stoyanov, S.,
Hendriks, M., 2005. Failure and success factors of
educational ICT projects: a group concept mapping
approach, British Journal of Educational Technology,
36, (4) 2005, 681–684
Zadeh L. A., 1965. Fuzzy Set, Information and control, v.
8, pp.338-353
Zadeh L. A., 1973. Outline of new approach to the
analysis of complex systems and decision processes,
IEEE Transactions on systems, man, and cybernetics,
vol. SMC-3, No.1, January 1973, pp.28-44
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
508
