
FUZZY CLASSIFIER BASED ON SUPERVISED CLUSTERING
WITH NONPARAMETRIC ESTIMATION OF LOCAL
PROBABILISTIC DENSITIES IN DEFAULT
PREDICTION OF SMALL ENTERPRISES
Maria Luiza F. Velloso, Nival N. Almeida, Thales Ávila Carneiro
Department of Eletronics, Rio de Janeiro State University, São Francisco Xavier 524, Rio de Janeiro, Brazil
José Augusto Gonçalves do Canto
Institute of Political Science and Economics, Candido MendesUniversity, Rio de Janeiro, Brazil
Keywords: Supervised clustering, Fuzzy modelling, Interpretability.
Abstract: The accuracy-complexity trade-off has been an important issue in system modeling. Parsimonious
modelling is preferred to complex modelling and, of course, accurate modelling is preferred to inaccurate
modelling. In system modelling with fuzzy rule-based systems, the accuracy-complexity tradeoff is often
referred as the interpretability-accuracy trade-off, and high interpretability is the main advantage of fuzzy
rule-based systems over other nonlinear systems. In many applications, gaining knowledge about the
system, in an understandable way, is as important as getting accurate results. The classical fuzzy classifier
consists of rules each one describing one of the classes. In this paper we use a fuzzy model structure where
each rule represents more than one class with different probabilities. The rules are extracted through
clustering and the probabilities are estimated in a local (cluster by cluster) non-parametric way. This
approach is applied to predict default in small and medium enterprises in Brazil, using indexes that reflect
the financial situation of enterprise, such as profitable capability, operating efficiency, repayment capability
and situation of enterprise’s cash flow. The preliminary results show a significant improvement in the
interpretability, without accuracy loss, compared with other approaches.
1 INTRODUCTION
Extracting a small set of rules to make an accurate
and efficient system is one of the most addressed
fuzzy modelling tasks. One basic motivation to
implement a fuzzy model lies in its transparency.
High interpretability is the main advantage of fuzzy
rule-based systems over other nonlinear systems.
The accuracy-complexity trade-off in general
modelling is often referred to as the interpretability-
accuracy trade-off in fuzzy modelling.
The aim of this work is to propose a modelling
using mechanisms to improve the accuracy of fuzzy
models based in supervised clustering (Abonyi,
2003) without loss of interpretability.
The classical fuzzy classifier consists of rules
each one describing one of the C classes. In
probabilistic fuzzy classifiers the consequent part is
defined as the probabilities that a given rule
represents the C classes, and one rule can represent
more than one class with different probabilities
(Abonyi, 2003; Roubos, 2003; Lee, 2008; Hengjie,
2011). In a probabilistic fuzzy classifier,
probabilities are assigned to all the class labels in the
consequent parts of the rules. In this paper we use a
fuzzy model structure where each rule represents
more than one class with different probabilities. A
supervised clustering algorithm is used for the
identification of this fuzzy model and a
nonparametric estimation of the probabilities of the
classes in the consequents of rules.
The issue of credit availability to small firms has
garnered world-wide concern recently. Small and
Medium Enterprises (SMEs) are almost 99% of the
total number of firms in Brazil, and they offer 78%
of the jobs in the country. But, around 80% of SMEs
509
F. Velloso M., N. Almeida N., Ávila Carneiro T. and Augusto Gonçalves do Canto J..
FUZZY CLASSIFIER BASED ON SUPERVISED CLUSTERING WITH NONPARAMETRIC ESTIMATION OF LOCAL PROBABILISTIC DENSITIES IN
DEFAULT PREDICTION OF SMALL ENTERPRISES.
DOI: 10.5220/0003675305090512
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 509-512
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

is shut down before one year of activity. Many
public and financial institutions launch each year
plans in order to sustain this essential player of
nation economies (Altman, Sabato, 2006).
Borrowing remains undoubtedly the most important
source of external SME financing.
Small firms may be particularly vulnerable
because they are often so informationally opaque,
and the informational wedge between insiders and
outsiders tends to be more acute for small
companies, which makes the provision of external
finance particularly challenging (Berger, Udell,
2002). Some financial ratios are used in the context
of default prediction in small and micro firms
operating in a state of Brazil and we choose some of
them, as described in Section 3. Although the
enterprise’s wish of returning loan, which is
represented by the rate of returning interests, we
often don’t have any information about the amount
of interests that has been repaid by enterprises that
are requiring a loan for the first time. In this case,
the prediction of default relies on information in the
balance sheet of these enterprises.
Our approach is applied to predict default in
small and medium enterprises in Brazil, using
indexes that reflect the financial situation of
enterprise. The results show a significant
improvement in the interpretability, without
accuracy loss, compared with other approaches.
The paper is organized as follows. In Section 2,
the structure of the new fuzzy classifier is presented.
For the estimation of probability density functions
for each class in each cluster based on a
nonparametric method is presented in Section 3. The
proposed approach is studied for default prediction
in small and medium enterprises in Section 4.
Finally, the conclusions are given in Section 5.
2 FUZZY CLASSIFIER
STRUCTURE
2.1 The Classical Fuzzy Classifier
The classical fuzzy rule-based classifier consists of
fuzzy rules each one describing one of the C classes.
The rule antecedent defines the operating region of
the rule in the n-dimensional feature space and the
rule consequent is a crisp (nonfuzzy) class label
from the {
,
,
....,
} label set:
r
i
: If x
1
is
,
and . . . x
1
is
,
then =
(1)
where
,
; . . . ;
,
are the antecedent
fuzzy sets and w
i
is a certainty factor that represents
the desired impact of the rule.
The and connective is modelled by the
product operator. The output of the classical fuzzy
classifier is determined by the winner takes all
strategy, i.e. the output is the class related to the
consequent of the rule that gets the highest degree of
activation:
=
∗
,
∗
=max
(2)
To represent the
,
fuzzy set, we use
Gaussian membership functions.
2.2 Probabilistic Fuzzy Classifier
One of the possible extensions of the classical
quadratic Bayes classifier is to use mixture of
models for estimating the class-conditional densities.
In these solutions each conditional density is
modelled by a separate mixture of models. In
(Abonyi, 2003) the
|
posteriori densities are
modelled by R > C mixture of models (clusters). The
consequent of the fuzzy rule is defined as the
probabilities of the given rule represent the
,
,
....,
classes:
r
i
: If x
1
is
,
and . . . x
1
is
,
then
=
ℎ
|
,...,
=
ℎ
|
.
(3)
Classical fuzzy clustering algorithms are used to
estimate the distribution of the data. Hence, they do
not utilize the class label of each data point available
for the identification. Furthermore, the obtained
clusters cannot be directly used to build the
classifier. In the following a new cluster prototype
and the related distance measure will be introduced
that allows the direct supervised identification of
fuzzy classifiers. As the clusters are used to obtain
the parameters of the fuzzy classifier, the distance
measure is defined similarly to the distance measure
of the Bayes classifier:
1
,
,
=
=
−
1
2
,
−
,
,
×
=
ℎ
(4)
This distance measure consists of two terms. The
first term is based on the geometrical distance
between the
cluster centres and the x
k
observation
vector, while the second is based on the probability
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
510
that the rith cluster describes the density of the class
of the kth data,
=
. The proposed
approach estimate the second term by non-
parametric estimation of the probability densities of
each class in each cluster (r
i
), described in the next
section.
3 PROBABILITY ESTIMATION
The estimation of local probability densities for each
class in each cluster is based on the original
Probabilistic Neural Network (PNN). PNN (Bishop,
1995) is a network formulation of probability
density estimation. A PNN consists of several sub-
networks, each of which is a Parzen window PDF
estimator for each of the classes. The input nodes are
the set of measurements. The second layer consists
of the Gaussian functions formed using the given set
of training data points as centres. The third layer
performs an average operation of the outputs from
the second layer for each class. The fourth layer
performs a vote, selecting the largest value. The
associated class label is then determined. The PNN
is a classifier version, which combines the Baye’s
strategy for decision-making with a non-parametric
estimator for obtaining the probability density
function (PDF).
4 DEFAULT PREDICTION
The sample data set comes from a state-owned
commercial bank. The original dataset contains 126
instances however 3 of these are omitted because
these are incomplete data, which is common with
other studies. The class distribution is 51% default
and 42% non-default. The 123 samples represent
Small and Medium Enterprises of only one state of
Brazil. Among these enterprises, the number of the
enterprises which could repay the loan is 60, the rest
63 are those which could not repay the loan.
Our model is an accounting based model. In this
kind of model, accounting balance sheets are used
and the input indexes include the enterprise’s
capability of returning loan and wish of returning
loan, and in this work the capability was analysed.
The capability of returning loan is measured by
several indexes that reflect the financial situation of
enterprise, such as profitable capability, operating
efficiency, repayment capability and situation of
enterprise’s cash flow, etc. Four accounting financial
ratios were chosen (these are the most common used
indexes). These are as follows:
X1 = Earnings before taxes / Average total assets
X2 = Total liabilities / Ownership interest
X3 = Operational cash flow / Total liabilities
X4 = Working capital / Total assets.
Each index represented the average of three
periods before the prediction period.
We limited the number of clusters in 5, in order
to maintain good interpretability. The best results are
obtained using three clusters. Therefore, our rule
base has three rules.
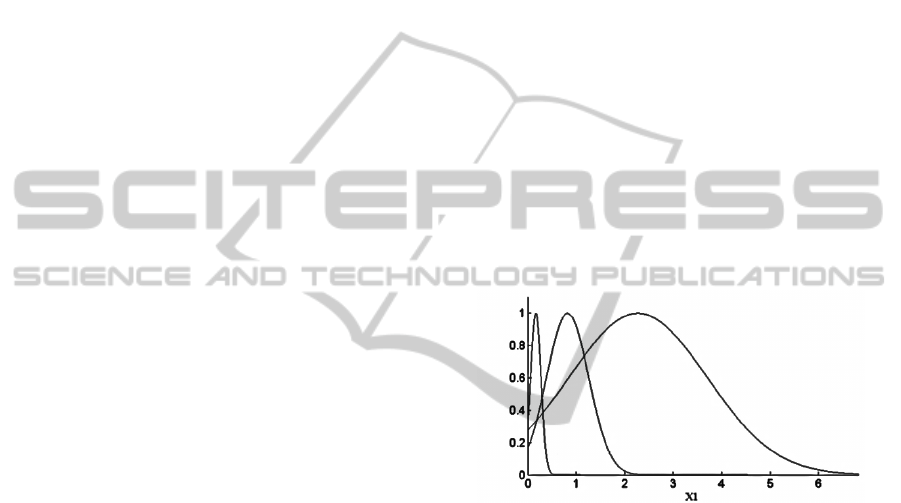
Some membership functions, related to variable
X1, obtained by fuzzy clustering are illustrated in
Figure 1. Clusters have different covariance
matrices, and they are diagonal matrices, in order to
project memberships on original variables. The
algorithm did not optimize clustering based on
interclass separability.
The estimated densities projected on the original
input variable X1 are illustrated by Figure 2. This
figure shows the densities related to variable X1 for
the two classes related to one cluster.
Figure 1: Membership functions related to variable X1 in
the three clusters (rules).
The performance of the obtained classifiers was
measured by leave-one-out cross validation As the
name suggests, leave-one-out cross-validation
(LOOCV) involves using a single observation from
the original sample as the validation data, and the
remaining observations as the training data. This is
repeated such that each observation in the sample is
used once as the validation data.
The results are summarized in Table 1. We
report the mean values of the error. For the proposed
approach, Model 1, the number of rules is equal to
the number of clusters. The grid partition approach,
Model 3, has 20 rules, and the other approach that
uses clustering and probabilities, Model 2 (Abonyi,
2003), has three rules. The proposed approach is
much more compact (in terms of the number of
rules) than the grid approach and more accurate.
Although the proposed approach requires more
memory (training data must be available in
FUZZY CLASSIFIER BASED ON SUPERVISED CLUSTERING WITH NONPARAMETRIC ESTIMATION OF
LOCAL PROBABILISTIC DENSITIES IN DEFAULT PREDICTION OF SMALL ENTERPRISES
511
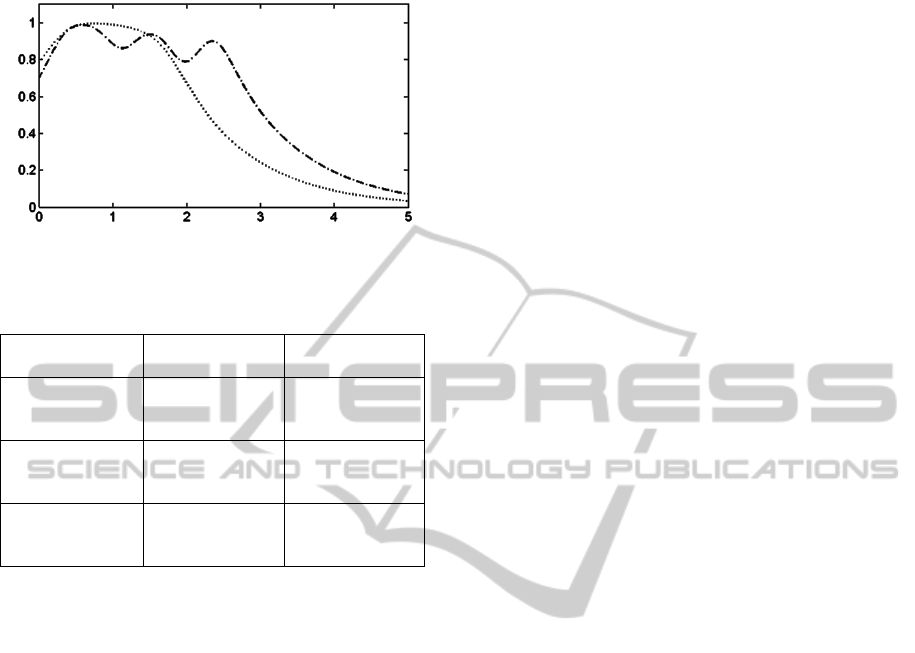
classification mode), it is more accurate.
Figure 3: Probability densities of two classes related to X1
in cluster 1.
Table 1: Results.
Model Rule Number Overall
accuracy
Model 1
(proposed
approach)
3 92%
Model 2
(supervised
clustering)
3 80%
Model 3
(traditional grid
partition)
20 95%
5 CONCLUSIONS
In this paper we use a fuzzy model structure where
each rule represents more than one class with
different probabilities. The rules are extracted
through clustering and the probabilities are
estimated in a local (cluster by cluster) non-
parametric way. This approach is applied to predict
default in small and medium enterprises in Brazil,
using indexes that reflect the financial situation of
enterprise, such as profitable capability, operating
efficiency, repayment capability and situation of
enterprise’s cash flow. In this work, we can see that
clusters do not present enough separability, specially
related to X4. We intend conduct research in order
to extract rules with improved interpretability,
combining with feature reduction. Estimation of
PDFs can be experimented without crisp boundaries.
Others comparisons could be experimented. In spite
of the simplicity adopted, the preliminary results
show a significant improvement in the
interpretability, without accuracy loss, compared
with other approaches.
ACKNOWLEDGEMENTS
The financial support from Brazilian research
agency Carlos Chagas Filho Foundation for
Research Support of Rio de Janeiro State (FAPERJ)
is gratefully acknowledged.
REFERENCES
Abonyi, J, Szeifert, F., 2003. Supervised fuzzy clustering
for the identification of fuzzy classifiers, Pattern
Recognition Letters 24, pages 2195–2207
Altman1, Edward I., Sabato, Gabriele, 2007. Modelling
Credit Risk for SMEs: Evidence from the U.S. Market.
Abacus, Volume 43, Issue 3, pages 332–357.
Behr, P. and Güttler, A. (2007), Credit Risk Assessment
and Relationship Lending: An Empirical Analysis of
German Small and Medium-Sized Enterprises.
Journal of Small Business Management, 45, pages
194–213.
Bishop, C. M., 1995. Neural Networks for Pattern
Recognition. Oxford University Press, Oxford.
Casillas, J.; Cordón, O.; Herrera Triguero, F.; Magdalena,
L. (Eds.), 2003. Accuracy Improvements in Linguistic
Fuzzy Modelling Series: Studies in Fuzziness and Soft
Computing, Vol. 129 , Springer.
Gath, I., Geva, A.B., 1989. Unsupervised optimal fuzzy
clustering. IEEE Trans. Pattern Anal. Machine Intell
7, pages 773–781.
Lee, Hyong-Euk, Park, Kwang-Hyun, and Bien,
Zeungnam Zenn, 2008. Iterative Fuzzy Clustering
Algorithm With Supervision to Construct Probabilistic
Fuzzy Rule Base From Numerical Data, IEEE
Transactions On Fuzzy Systems, Vol. 16, No. 1, pages
263- 277.
Roubos, Johannes A, Setnes, Magne, Abonyi, Janos, 2003.
Learning fuzzy classification rules from labeled data.
Information Sciences—Informatics and Computer
Science: An International Journal - Special issue on
recent advances in soft computing Volume 150 Issue
1-2, Publisher Elsevier Science Inc. New York, NY,
USA
FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications
512
