
NEUROFUZZY MIN-MAX NETWORKS IMPLEMENTATION
ON FPGA
Alessandro Cinti and Antonello Rizzi
Department of Information Engineering, Electronics and Telecommunications, University of Rome “La Sapienza”
Via Eudossiana 18, 00184, Rome, Italy
Keywords: Neural networks, Neurofuzzy networks, Hardware acceleration, Min-max classifiers, FPGA.
Abstract: Many industrial applications concerning pattern recognition techniques often demand to develop suited low
cost embedded systems in charge of performing complex classification tasks in real time. To this aim it is
possible to rely on FPGA for designing effective and low cost solutions. Among neurofuzzy classification
models, Min-Max networks constitutes an interesting tool, especially when trained by constructive, robust
and automatic algorithms, such as ARC and PARC. In this paper we propose a parallel implementation of a
Min-Max classifier on FPGA, designed in order to find the best compromise between model latency and
resources needed on the FPGA. We show that by rearranging the equations defining the adopted
membership function for the hidden layer neurons, it is possible to substantially reduce the number of logic
elements needed, without increasing the model latency, i.e. without any need to lower the classifier working
frequency.
1 INTRODUCTION
Present Pattern Recognition applications deal with
more and more complex patterns and often have to
manage huge databases. Efficient solutions are based
on Soft Computing techniques, where algorithms are
usually characterized by a remarkable computational
complexity. Moreover, several applications are
thought for real-time processing, introducing very
stringent constrains on the working frequency of a
classification model. For this reason, it becomes
essential the possibility of accelerating in hardware
the functions with the higher complexity. To this
aim, if we consider only low cost solutions, two
different approaches are nowadays available. The
first one relies on GPU (Graphic Processing Unit),
powerful parallel processors on board of common
graphics cards capable of 3D hardware
accelerations, usually through some high level
programming languages such as CUDA. The second
solution consists in employing a FPGA (Field
Programmable Gate Array) based embedded system.
A FPGA is a user-programmable integrated circuit
that can be thought as an array of reconfigurable
logic blocks (LBs), linked by a hierarchy of
reconfigurable interconnections. Programming a
FPGA simply means to use and configure a subset of
LBs and defining data links between them in order
to realize a given digital system. The inherent
parallelism of the logic resources on a FPGA allows
for considerable computational throughputs even at
low MHz clock rates. With respect to GPUs, FPGAs
are much more flexible tools for parallel
implementation of a given algorithm, without any
need to be constrained to the predefined array of
processors (called “Grid of Thread blocks”) in GPU
integrated circuits. In the technical literature related
to Soft Computing and Pattern Recognition fields
it’s possible to find many FPGA implementations of
complex algorithms. In particular, there are very
interesting papers dealing with the hardware
implementation of neural networks and fuzzy
systems on FPGA (Jingyan Xue, 2009), (Uppalapati,
2009), (Oliveira, 2010), (Wan De Weng, 2007). Our
research team has successfully faced several pattern
recognition problems using neurofuzzy classifiers,
adopting neurofuzzy Min-Max networks trained by
ARC (Adaptive Resolution Classifiers) and PARC
(Pruning ARC) algorithms (Rizzi, 2002), such as the
ones described in (Rizzi, 2008), (Rizzi, 2009), (Del
Vescovo, 2010). In fact, among neuro-fuzzy
classifiers, Simpson’s Min-Max networks have the
advantage to be trained in a constructive way. ARC
and PARC training algorithms are characterized by a
51
Cinti A. and Rizzi A..
NEUROFUZZY MIN-MAX NETWORKS IMPLEMENTATION ON FPGA.
DOI: 10.5220/0003680700510057
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 51-57
ISBN: 978-989-8425-84-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)
high automation degree and allow to synthetize Min-
Max neurofuzzy networks with a remarkable
generalization capability. For this reason we have
planned to adopt Min-Max neurofuzzy classifiers as
the core of some real time pattern recognition
applications, facing in a first step the design of
embedded systems characterized by high
performances. To this aim we started to implement
Min-Max networks on FPGA, searching for the best
compromise between parallelization degree and
hardware resources request, in terms of the number
of LBs. In this paper we propose an efficient
solution representing an interesting compromise
between the above mentioned objective functions.
2 MIN-MAX NEUROFUZZY
NETWORKS: AN OVERVIEW
From the point of view of data driven modelling
techniques, many practical applications concerning
diagnostic and identification problems can be
expressed and solved as classification problems.
Basically a classification problem can be defined as
follows. Let P: R
N
→ L be an unknown oriented
process to be modelled, where R
N
is the domain set
and the codomain L is a label set, i.e. a set in which
it is not possible (or misleading) to define an
ordering function and, hence, any dissimilarity
measure between its elements. Let K be the number
of classes in L. Let S
tr
and S
ts
be two sets of input-
output pairs, namely the training set and the test set,
subject to the constrain S
tr
∩ S
ts
= Ø. Once fixed a
target model family T, a training algorithm is in
charge of synthetizing a particular instance T
*
of T,
exclusively on the basis of the information contained
in S
tr
, such that the classification error of T
*
computed on S
ts
will be minimized.
Once trained, a classification model should be
able to classify correctly any N-dimensional input
vector x belonging to the classification process
domain (generalization capability).
The Min-Max classification strategy consists in
directly defining the decision regions of the
unknown classification process to be modeled by
covering the patterns of the training set with
hyperboxes. This technique has been originally
proposed in (Simpson, 1992).
A hyperbox defined in R
N
is a finite polyhedral
region delimited by 2N hyperplanes, each
constrained to be parallel to the coordinate axes of
the input space reference system. On the basis of
these constraints, it is possible to establish
univocally the size and the position of each
hyperbox by means of two vertices, namely the
minimum (Min) point v and the maximum (Max)
point w, where v and w are respectively the closest
and the farthest vertices to the origin of the domain
reference system. Since we are facing an exclusive
classification problem, each hyperbox is associated
with a unique class label k. Several hyperboxes can
be associated with the same class label k. With the
notation HB
jk
we mean that the j-th hyperbox is
associated with the class label k, and the number of
hyperboxes associated with this class label is J
k
.
Considered as a crisp set, each hyperbox can be
fuzzified by associating with it a membership
function. In the following we will consider the
membership function proposed by Simpson
(Simpson, 1992), in which the slope outside the
hyperbox HB
jk
is established by the real and positive
fuzziness parameter γ, i.e.:
(
)
()()()
−
=
−−−−=
=
1N
0i
ii
γ;xvfγ;wxf1
N
1
γ;,,
ijkijk
jkjkjk
wvx
μ
(1)
We define
()
γz,f as a soft-limiter function:
()
>
≤≤
<
=
1γz1,
1γz0γz,
0γz,0
γz;f
(2)
where z is a real positive number.
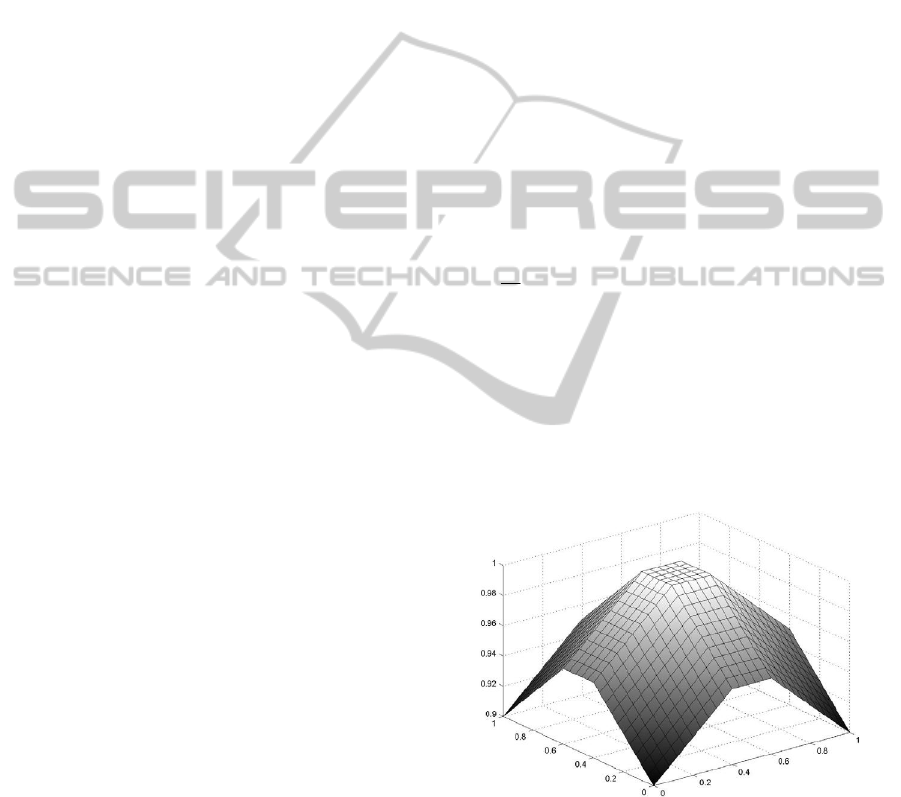
Figure 1: The hyperbox membership function with γ = 0.5.
Figure 1 shows the typical shape of the original
Simpson’s membership function in the case of a two
dimensional (N = 2) support space for γ = 0.5.
A Min-Max classification model is a feed-
forward three-layer neural network (see Figure 2).
The first layer is a dummy one, aiming only to
supply the input features to each neuron of the
NCTA 2011 - International Conference on Neural Computation Theory and Applications
52
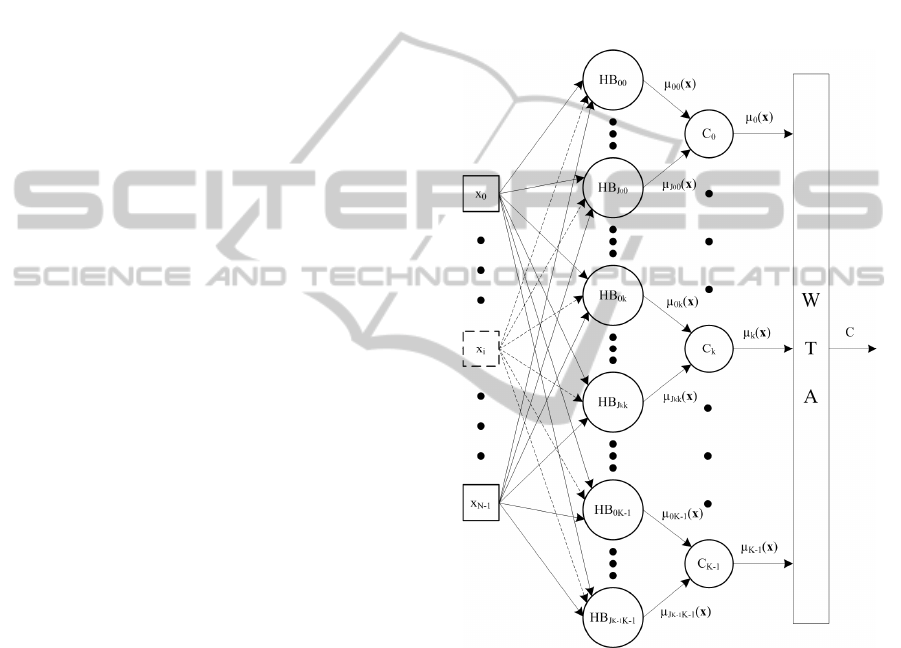
second (hidden) layer. Each neuron of the hidden
layer corresponds to a hyperbox and it computes the
membership of the input pattern with respect to that
hyperbox. Adopting the same notation used so far,
we can say that the total number M of neurons in the
hidden layer is:
−
=
=
1
0
K
k
k
JM
(3)
Let J be the class represented by the higher number
of hyperboxes, i.e:
()
k
Kk
JJ
10
max
−≤≤
=
.
(4)
The third (output) layer is composed of one neuron
for each class. Each neuron of the output layer
determines the fuzzy membership value of the input
pattern with respect to the corresponding class, by
computing the fuzzy union of the outputs of all
neurons in the hidden layer associated with the
corresponding class k, i.e:
() ()
(
)
10
jkk
μmaxμ
−≤≤
=
k
Jj
xx
(5)
Since the input space dimension N and the number
of classes K are fixed by the classification problem,
it is obvious to state that the structural complexity of
a Min-Max network is directly represented by the
total number M of neurons in the hidden layer.
When dealing with exclusive classification
problems, the class corresponding to the maximum
membership value is selected as the output class
label (winner takes all strategy, WTA in Figure 2),
i.e.:
()()
10
k
μmaxarg
−≤≤
=
Kk
C x
(6)
When computing the classification performance on a
test set, if C is different from the target output label
(the class label associated with the input pattern
x in
the test set), we have an error. If more than one class
reaches the maximum membership value, we have
an indetermination. Starting from a given training
set, a constructive learning algorithm for a Min-Max
network must establish the number, position and size
of each hyperbox. To this aim, we use the Adaptive
Resolution Classifier (ARC) and Pruning Adaptive
Resolution Classifier (PARC) learning algorithms. A
detailed description of ARC/PARC training
procedure can be found in (Rizzi, 2002).
3 FPGA TARGETED
IMPEMENTATION
In this work we propose an interesting
implementation for the Min-Max classification
model targeted to a FPGA hardware device. We
have considered a FPGA implementation because it
offers the best tradeoff between cost and
customizability. The latter factor reveals to be
essential for computational cost and hardware
complexity to be reduced.
Figure 2: The structure of a Min-Max neurofuzzy
classifier.
As concerns similar works, in (Liang, Y., 2006) a
FPGA implementation of a Min-Max neural network
called MRC-FMMC is proposed. This classifier is a
variant of the classical Min-Max network proposed
by Simpson (described in the previous section) and
it is based on the computation of a fuzzy hyperbox
reliability. For this reason, any comparison with our
targeted FPGA implementations is not significant.
In this section, we will propose both a plain
implementation and an optimized one of a classical
Min-Max neural network. The presentation of a
plain implementation has the only purpose to
represent a term of comparison with the proposed
NEUROFUZZY MIN-MAX NETWORKS IMPLEMENTATION ON FPGA
53
optimized version. Even though the two
implementation strategies are different both the
architectures are based on the same constituent
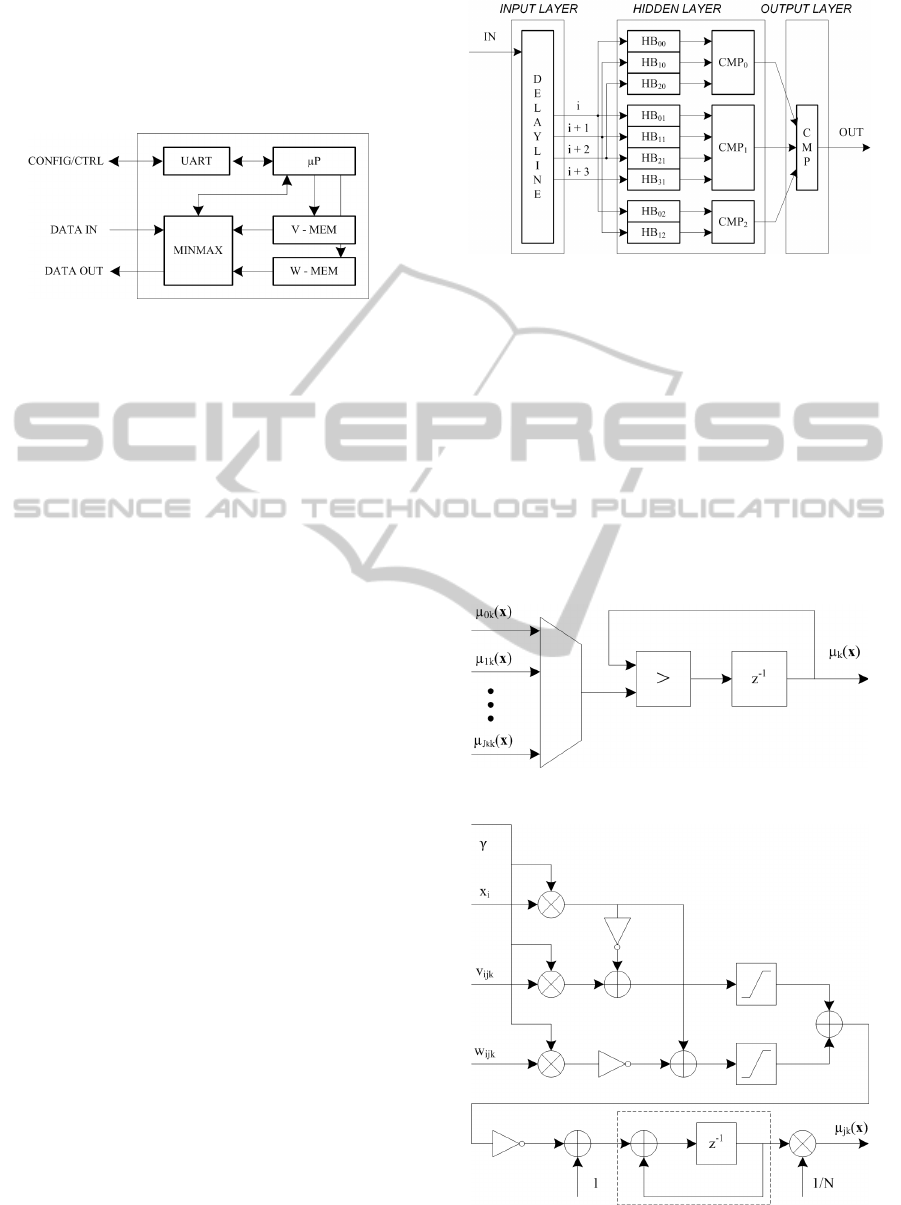
blocks. Figure 3 shows a conceptual scheme of the
implemented architecture.
Figure 3: Min-Max classification model functional
scheme.
The UART block is intended for creating both
configuration and control interfaces with an external
PC that communicates with the system accessing it
through the CONFIG/CTRL port. The V-MEM and
W-MEM blocks, as their names can suggest, are
memory blocks that contain respectively
v and w
hyperbox vertices.
The µP block represents a microprocessor in
charge of the following tasks: managing the memory
accesses by the UART block in both directions;
loading
γ into the MINMAX block and v and w
vertices respectively into the V-MEM and W-MEM
blocks; correctly transferring the vertices
v and w to
the hyperboxes during processing; managing all the
accesses to the MINMAX block configuration and
performance register.
The MINMAX block receives as input the
feature vector (DATA IN port) that has to be
classified, performs all the operations defined by
equations (1), (5) and (6), returning the class label
(DATA OUT port).
The MINMAX block is the main processing
element and since most of the differences between
the plain and the optimized versions of the classifier
are at hyperbox level we will explain it in a greater
detail. The MINMAX block conceptual scheme is
shown in Figure 4, that depicts the three-layer
structure of a Min-Max neural network.
Once the system is configured, the input data is
ready to be processed. Each N-dimensional input
vector requires N clock cycles to completely enter
and feed the classification model. This is realized
using a DELAYLINE with length J, as defined in
Equation (4), so that all the j-th hyperboxes (each
one belonging to a different class k) receive the
samples from the same tap of the delayline. We
exploited this structural choice to use just one
comparator to calculate
()
x
k
μ as in Figure 5.
Figure 4: MINMAX block conceptual scheme.
As shown in Figure 4 the K comparators (class
comparison blocks CMP
0
, CMP
1
, CMP
2
) compute
the values (5) entering the final comparator CMP
(output layer) that produces the class label
identifying which class
x belongs to, as described in
(6). The hyperbox architecture that we implemented
for the plain version of the Min-Max classification
model is shown in Figure 6. Inspecting Figure 6 it’s
easy to recognize all the operations described in (1).
For example, the summation is implemented using
an accumulator as depicted within the rectangular
dashed line.
Figure 5: Comparator conceptual scheme.
Figure 6: Hyperbox implementation scheme (plain
version).
NCTA 2011 - International Conference on Neural Computation Theory and Applications
54

As we mentioned at the beginning of this section
we describe an efficient way to compute an
hyperbox memebership function. As we will see in
the following, by rearranging the terms in (1) it is
possible to synthesize a slight variation in the
classical Min-Max neural network architecture, in
which both computational and hardware cost
benefits are remarkable.
3.1 Efficient Computation of Fuzzy
Memberships
Let x be the N-dimensional input vector of a Min-
Max neural network made up of M hyperboxes. Let
v and w be, respectively, the sets of all the closest
and farthest vertices to the origin of a defined
reference system for all the hyperboxes.
We can express the j-th membership function
associated with the class label k defined in (1) as
follows:
(
)
()()()
()
N
γ;,,
1
γ;xvfγ;wxf
N
1
1
γ;,,μ
jkjkjk
1N
0i
iijkijki
jkjkjk
wvx
wvx
ρ
−=
=−+−−=
=
−
=
(7)
Exploiting the definition of the generic membership
function (2), we obtain the following expressions:
(
)
()
≤<+
+≤≤
<≤
=
=
1xw
γ
1
,1
w
γ
1
xw,w-xγ
wx0,0
γ;w-xf
iijk
ijkiijkijki
ijki
ijki
(8)
(
)
()
−<≤
≤≤−
≤<
=
=
γ
1
vx0,1
vx
γ
1
vx-vγ
1xv,0
γ;x-vf
ijki
ijkiijkiijk
iijk
iijk
(9)
Combining expressions (8) and (9) we can
distinguish five adjacent and disjointed intervals
(labeled from I to V) in which the following function
behaves differently:
(
)
(
)
()
()
≤<+
+≤<
≤≤
<≤−
−<≤
=
=+
V
IV
III
II
I
1,x
γ
1
w,1
,
γ
1
wxww-xγ
,wxv,0
,vx
γ
1
v,x-vγ
,
γ
1
vx0,1
γ;x-vfγ;w-xf
iijk
ijkiijkijki
ijkiijk
ijkiijkiijk
ijki
iijkijki
(10)
We rearrange the terms in (10) in order to highlight
the dependences with the variables defined as
follows:
=
=
=
ijkijk
ijkijk
ii
γww'
γvv'
γxx'
(11)
so that:
(
)
(
)
()
ijkijki
iijk
ijkiijkijki
ijkiijk
ijkiijkiijk
ijki
iijkijki
w',v',x'
,x'1w',1
,1w'x'w''-w'x'
,w'x'v',0
,v'x'1v',-x'v'
,1v'x'0,1
-x'v'f-w'x'f
ijk
V
IV
III
II
I
ρ
γ
=
=
≤<+
+≤<
≤≤
<≤−
−<≤
=
=+
(12)
To obtain the resulting value from the hyperbox
computing block we would have to make the
following steps: sum the value obtained in (12) for
all the N dimensions, divide the result by N, and then
subtract it to 1. According to (5), at this point, we
would have to compare all the membership function
values related to the hyperboxes associated to the
same class k, choosing the maximum one as the
overall class membership.
Since, by definition
(
)
1w',v',x'
ijkijki
≤
ijk
ρ
(13)
we can surely say that:
()
jk jk
', ' , '
jk
N
ρ
≤xv w
(14)
As a consequence, we can compare the membership
values of the two hyperboxes
HB
jk
and HB
(j+1)k
,
associated with the same class
k, relaying on the
following simplification:
NEUROFUZZY MIN-MAX NETWORKS IMPLEMENTATION ON FPGA
55

()
()
()(
())
k)1(k)1()1(
jkjk
k)1(k)1()1(
jkjk
',','
,',','min
',','
1
,
',','
1max
+++
+++
=
=
−
−
jjkj
jk
jjkj
jk
N
N
wvx
wvx
wvx
wvx
ρ
ρ
ρ
ρ
(15)
Neglecting the division by N and the subtraction
to 1 we have only rescaled and inverted the ordering
of
ρ
jk
functions related to the same class k.
Using this property we obtained a more efficient
hyperbox implementation that will be used in the
optimized version of the Min-Max classifier, as
described in Figure 7.
3.2 Optimized Implementation
The main structural difference between the plain and
the optimized versions resides obviously on the
implementation of the hyperbox, as it can be seen
comparing Figure 6 to Figure 7.
Figure 7: Hyperbox implementation scheme (optimized
version).
Moreover the V-MEM and W-MEM blocks in
Figure 3, in the optimized version will contain
respectively
v’ and w’ vertices, that are the pre-
multiplied by γ versions of the hyperboxes vertices
v
and w (11). We also have to add a multiplier to the
beginning of the DELAYLINE in Figure 4, so that
hyperboxes will receive
x’ instead of x. Finally,
according to the result obtained in (15), we have to
change the order relation that comparison blocks C
0
,
C
1
, …, C
K-1
and WTA represented in Figure 2
respectively perform in (5) and (6), from maximum
to minimum.
3.3 Performance Comparison
The latency of the system D, expressed in number of
clock cycles necessary to calculate the output class
is
()
2
11
+++=
=++++=
K
N
J
KNJD
(16)
where J is the length of the DELAYLINE (input
layer),
N + 1 is the number of clock cycles necessary
for a hyperbox to calculate its result, 1 clock cycle of
delay due to class comparison blocks (hidden layer)
and
K is the number of the class labels,
corresponding to the number of clock cycles
necessary to calculate the last comparison (output
layer). The latency value is exactly the same in both
versions.
Looking at the differences in term of
combinational resources, from Figure 6 and Figure 7
we find that to implement an hyperbox in the plain
version we need 4 adders and 4 multipliers, while in
the optimized version we only need 3 adders. In this
computation we considered that a subtraction
operation is performed by an adder and a division
operation is performed by a multiplier. Since the
number of the hyperboxes in the system is
M, we
can say that to implement a complete Min-Max
classification system in the plain version we need
4
M adders and 4M multipliers, while in the
optimized version we only need 3
M adders and 1
multiplier (the one at the top of the DELAYLINE).
As a further result it is possible to observe that
by construction, for all
i, j, k, we have:
≤+
≥−
≤
1
γ
1
w
0
γ
1
v
wv
ijk
ijk
ijkijk
(17)
hence, obtaining:
()
ijkijk
,,
w1,vmin
1
γ
−
≥
kji
.
(18)
NCTA 2011 - International Conference on Neural Computation Theory and Applications
56

This result means that γ has a lower limit that
depends on the choice of the vertices that describe
the hyperboxes belonging to every class. Choosing
its value below threshold highlighted in (18) doesn’t
have any effect on changing the slope of the
membership function defined by (1) and (2). This
constrain should be taken into consideration in any
tweaking procedure for the γ parameter aimed at
selecting a suited fuzziness degree for the
neurofuzzy classifier behavior.
4 CONCLUSIONS
Min-Max neural networks together with ARC/PARC
training procedures constitute a powerful, effective
and automatic classification system, well suited to
deal with complex diagnostic and identification
tasks to be performed in real-time. In this paper we
propose both a plain implementation and an
optimized one of a classical Min-Max neural
network, targeted to FPGA. The main structural
difference between the plain and the optimized
versions concerns the implementation of the
hyperbox block. We have shown that by rearranging
the fuzzy membership function expression, it is
possible to obtain a circuit characterized by the same
latency, with a significant saving in terms of FPGA
resources.
We plan to develop specific embedded systems
based on the proposed optimized implementation to
be used in a wide range of possible applications. In
particular we are designing a dedicated appliance for
real-time fault diagnosis in electric machines and for
on the fly TCP/IP application flows identification.
ACKNOWLEDGEMENTS
Authors wish to thank Altera Corporation for the
useful support provided through a specific
University Program concerning our research
activity. Special thanks to Dr. Achille Montanaro, as
the Altera Account Manager and the Italian Altera
University Program Manager.
REFERENCES
Jingyan Xue, Laijun Sun, Mingliang Liu, Changming
Qiao, Guangzhong Ye, 2009, “Research on high-speed
fuzzy reasoning with FPGA for fault diagnosis expert
system” International Conference on Mechatronics
and Automation ICMA.
Uppalapati, S., Kaur, D., 2009, “Design and
Implementation of a Mamdani fuzzy inference system
on an FPGA” Fuzzy Information Processing Society,
NAFIPS.
Oliveira, D. N., de Lima Henn, G. A., da Mota Almeida,
O., 2010, “Design and implementation of a Mamdani
Fuzzy Inference System on an FPGA using VHDL”,
Fuzzy Information Processing Society NAFIPS.
Wan-De Wenig, Rui-Chang Lin, 2007, “An FPGA-Based
Neural Network Digital Channel Equalizer”,
International Conference on Machine Learning and
Cybernetics, Vol. 4, pp. 1903 - 1908.
Liang, Y, Fan, S. Q., Jin, D. M., 2006, The Hardware
Implementation of A Multi-resolution Combined
Fuzzy Min-Max Classifier Chip, ICICIC '06, First
International Conference on Innovative Computing,
Information and Control, Vol. 2, pp. 30 - 33.
Rizzi A., Panella M., Frattale Mascioli F. M., 2002,
“Adaptive Resolution Min-Max Classifiers”, IEEE
Transactions on Neural Networks, Vol. 13, No. 2, pp.
402 - 414.
Rizzi, A., Buccino, N. M., Panella M., Uncini, A., 2008
“Genre Classification of Compressed Audio Data”,
International Workshop on Multimedia Signal
Processing.
Rizzi, A., Frattale Mascioli, F. M., Baldini, F., Mazzetti,
C., Bartnikas, R., 2009, “Genetic Optimization of a
PD Diagnostic System for Cable Accessories”, IEEE
Transactions on Power Delivery.
Del Vescovo, G., Paschero, M., Rizzi, A., Di Salvo, R.,
Frattale Mascioli, F. M., 2010, “Multi-fault diagnosis
of rolling-element bearings in electric machines”, XIX
International Conference on Electrical Machines.
NEUROFUZZY MIN-MAX NETWORKS IMPLEMENTATION ON FPGA
57
