MODELING OF ABRASIVE WATER JET MACHINING USING

TAGUCHI METHOD AND ARTIFICIAL NEURAL NETWORKS

Menelaos Pappas

, Ioannis Ntziantzias

, John Kechagias

1,2

and Nikolaos Vaxevanidis

2,3

Department of Mechanical Engineering, Technological Educational Institute of Larissa, Larissa 41110, Greece

Department of Mechanical Engineering, University of Thessaly, Volos 38334, Greece

Department of Mechanical Engineering Educators, School of Pedagogical and Technological Education (ASPETE)

N. Heraklion 14121, Athens, Greece

Keywords: Abrasive Water Jet Machining (AWJM), Artificial Neural Networks (ANN), Taguchi Method, Surface

Quality, Process Parameters.

Abstract: This work presents a hybrid approach based on the Taguchi method and the Artificial Neural Networks

(ANNs) for the modeling of surface quality characteristics in Abrasive Water Jet Machining (AWJM). The

selected inputs of the ANN model are the thickness of steel sheet, the nozzle diameter, the stand-off distance

and the traverse speed. The outputs of the ANN model are the surface quality characteristics, namely the

kerf geometry and the surface roughness. The data used to train the ANN model was selected according to

the Taguchi’s design of experiments. The acquired results indicate that the proposed modelling approach

could be effectively used to predict the kerf geometry and the surface roughness in AWJM, thus supporting

the decision making during process planning.

1 INTRODUCTION

The AWJM belongs to the non-conventional

material removal methods and is used in industry to

machine different materials ranging from soft,

ductile to hard and brittle materials. This process

does not produce dust, thermal defects or fire

hazards. It is a good process for shaping composite

materials and imparts almost no surface

delamination see Momber and Kovacevic, 1997 and

Wang and Wong, 1999.

The primary interests in TRIP sheet steel

processing are the kerf shape (kerf width and kerf

taper) and surface quality (surface roughness of cut),

as well as burrs which may be formed at the jet exit

(Figure 1). Kerf shape and quality in slotting sheet

materials by AWJM and the resulting surface

roughness have been studied in recent research

works (Gudimetla, 2002; Hascalik, Ulas and Gurun

2007; Jegaraj and Babu, 2007; Valicek et al., 2007).

The innovation of the present work relies on the

use of a hybrid modeling approach based on the

Taguchi method and the Artificial Neural Networks

(ANNs) for the modeling of surface quality

characteristics in Abrasive Water Jet Machining

(AWJM). The experiments were performed on two

transformation induced plasticity (TRIP) steel sheets

which were processed using AWJM with three

different diameters of the nozzle (nozzle diameter),

three different distance values between the nozzle

and the sheet steel (stand-off distance) and three

different traverse speeds (also known as cutting

speed or travel speed). The selected inputs of the

ANN model are the thickness of steel sheets, the

nozzle diameter, the stand-off distance and the

traverse rate (cutting speed). The outputs of the

ANN model are the surface quality characteristics,

namely the kerf geometry and the surface roughness.

The data used to train the ANN model was selected

according to the Taguchi’s design of experiments

(DoE).

2 EXPERIMENTAL SETUP

Details concerning the experimental procedure and

the materials are given elsewhere; see Petropoulos et

al., 2009 and Vaxevanidis et al., 2010; therefore

only the main features are summarized below.

TRIP multi-phase steels belong to a new

generation of steel grades exhibiting an enhanced

combination of strength and ductility, with extensive

377

Pappas M., Ntziantzias I., Kechagias J. and Vaxevanidis N..

MODELING OF ABRASIVE WATER JET MACHINING USING TAGUCHI METHOD AND ARTIFICIAL NEURAL NETWORKS.

DOI: 10.5220/0003681103770380

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 377-380

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

applications in automotive and aerospace industry;

see Olson and Azrin, (1978). The TRIP steels tested

are designated as TRIP 800 HR-FH and TRIP 700

CR-FH. Specimens of both materials are of square

form (10x10 cm

) but differ in thickness, hardness

and processing method.

Machining was performed on a SIELMAN

HELLENIC HYDROJET industrial AWJM system.

In each specimen a slot of 3 cm in length was

cut. Each slot corresponds to different machining

conditions. After processing, each specimen was

separated in order to allow roughness measurements

to be performed on the machined surface.

The pressure at which a water jet operates is

about 400 MPa, which is sufficient to produce a jet

velocity of 900 m/s. Such a high-velocity jet is able

to cut materials such as ceramics, composites, rocks,

metals etc (Momber and Kovacevic, 1997).

Figure 1: Schematic representation of a typical cut in

AWJM.

The standard L

) orthogonal design of

experiments (DoE) technique was applied

(Kechagias, 2007; Kechagias et al., 2010; Pappas et

al., 2011). Columns 1, 2, 3, and 4 are assigned to

steel sheet thickness (A, mm), nozzle diameter (B,

mm), stand-off distance (C, mm), and traverse speed

(D, mm/min), respectively. The other columns were

left vacant (Table 1).

The measured quality indicators were the

arithmetic mean surface roughness (R

,) and the

mean kerf width.

measurements were performed with a

Surtronic 3+ stylus profilometer supported by

Talyprof® software. The cut-off length selected was

0.8 mm and the measurements were undertaken in

the direction of the cut. The parameter values appear

as averages of five measurements on each surface at

the medium area of the cut.

Table 1: Matrix Experiment.

Process Parameters

Performance

measures

No of

Exp.

A B C D Vacant

kerf

(mm)

(μm)

1 0.9 0.95 20 200 0.978 4.5

2 0.9 0.95 64 300 1.155 6.2

3 0.9 0.95 96 400 1.082 7.1

4 0.9 1.2 20 200 1.351 6.2

5 0.9 1.2 64 300 1.423 7.3

6 0.9 1.2 96 400 1.447 8.8

7 0.9 1.5 20 300 1.464 7.0

8 0.9 1.5 64 400 1.792 8.7

9 0.9 1.5 96 200 1.802 9.1

10 1.25 0.95 20 400 0.858 5.9

11 1.25 0.95 64 200 1.113 6.0

12 1.25 0.95 96 300 0.952 6.3

13 1.25 1.2 20 300 1.176 6.3

14 1.25 1.2 64 400 1.151 6.6

15 1.25 1.2 96 200 1.448 6.9

16 1.25 1.5 20 400 1.385 5.8

17 1.25 1.5 64 200 1.501 6.7

18 1.25 1.5 96 300 1.560 6.8

As it is illustrated in Figure 1 the kerf is of

tapered form and to evaluate this characteristic, the

semi-sum of the upper area width and the lower area

width were measured by a stereoscope (Petropoulos

et al., 2009).

3 MODELING FRAMEWORK

An ANN model was constructed that can predict

mean kerf diameter and mean surface roughness

), for every possible combination of values for

the four studied input parameters, namely the

thickness of steel sheet, the nozzle diameter, the

stand-off distance and the traverse speed. However,

the prediction capability of the model is more

efficient while the values of the parameters are

inside the valid ranges, which can be extracted from

the values summarized in Table 2.

Table 2: Parameter Design.

Process Parameters Units

Levels

1 2 3

A steel sheet thickness mm 0.9 1.25 -

B nozzle diameter mm 0.95 1.2 1.5

C stand-off distance mm 20 64 96

D traverse speed mm/min 200 300 600

steel sheet thickness

nozzle diameter

stand-off distance

traverse speed

kerf

Figure 2: Architecture of the neural network model.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

378

The model was created with the use of the

Neural Network Fitting Tool of Matlab

, which is

used for data fitting problems (Demuth and Beale,

2001). In fitting problems, neural network is used to

map between a data set of numeric inputs

(independent variables) and a set of numeric targets

(response variables).

A two-layer feed-forward network with five (5)

sigmoid hidden neurons and two (2) linear output

neurons was used in the frame of this modelling

approach. The network was trained with Levenberg-

Marquardt backpropagation algorithm. The neural

network architecture is presented in Figure 2.

The input data that was fed to the ANN model is

an 18x4 matrix, representing eighteen (18) samples

(number of experiments) of four (4) elements (steel

sheet thickness, nozzle diameter, stand-off distance

and traverse speed), while the target data is an 18x2

matrix, representing eighteen (18) samples of two

(2) elements (kerf and R

These 18 samples were randomly divided into

three subsets, namely the training, the validation and

the testing samples. The training subset that uses the

70% of the data (12 samples) is presented to the

network during training, and the network is adjusted

(define weight factors and bias) according to its

error. The validation subset that contains the 15% of

the data (3 samples) is used to measure network

generalization, and to halt training when

generalization stops improving. The testing subset

that uses the 15% of the data (3 samples) has no

effect on training and so provides an independent

measure of network performance during and after

training. This subset is used to compare output

(simulated data) and target (experimental data).

Training automatically stops when generalization

stops improving, as indicated by an increase in the

mean square error of the validation samples. Mean

Squared Error (MSE) is the average squared

difference between outputs and targets. Lower

values are better. Zero means no error. The MSE of

training of the created ANN was equal to 0.0425 and

its training took 12 epochs to complete. The best

validation performance is 0.10429 at epoch 6.

Regression values measure the correlation

between outputs and targets. An R value of 1 means

a close relationship, 0 a random relationship. The

regression analysis of the created ANN model

resulted to R values for training, validation and

testing, which were very close to 1, means a very

close relationship between the output (simulated

values) and the target (experimental values).

4 MODELING RESULTS

Based on the design variables for AWJM modeling

presented in Table 1, the performance measures

(surface quality characteristics) are tabulated in

Table 3. In the same Table the simulated results

obtained by the created ANN model as well as the

deviation between experimental (measured) and

simulated by ANN values are presented.

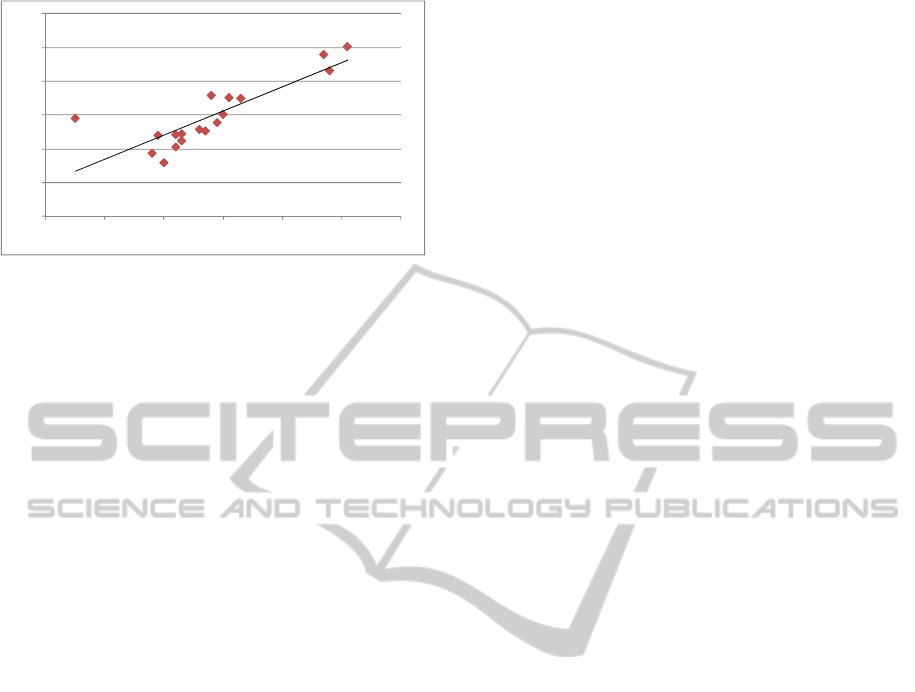
The correlation between experimental and

simulated data (neural network output) for kerf and

is shown in Figure 3 and 4 respectively.

A good correlation between experimental data

and simulated data (neural network output) both for

kerf and R

close to 0.7) is evident.

Table 3: Experimental and simulated by ANN values of

the performance measures (kerf and R

Experimental Simulated Deviation

Exp

kerf

(mm)

(μm)

kerf

(mm)

(μm)

kerf

(mm)

(μm)

1 0.978 4.5

1.231 6.9 0.253 2.4

2 1.155 6.2

0.946 6.0 -0.209 -0.2

3 1.082 7.1

1.035 7.5 -0.047 0.4

4 1.351 6.2

1.155 6.4 -0.196 0.2

5 1.423 7.3

1.391 7.5 -0.032 0.2

6 1.447 8.8

1.485 8.3 0.038 -0.5

7 1.464 7.0

1.525 7.0 0.061 0.0

8 1.792 8.7

1.734 8.8 -0.058 0.1

9 1.802 9.1

1.842 9.0 0.040 -0.1

10 0.858 5.9

1.092 6.4 0.234 0.5

11 1.113 6.0

0.865 5.6 -0.248 -0.4

12 0.952 6.3

1.094 6.4 0.142 0.1

13 1.176 6.3

1.217 6.2 0.041 -0.1

14 1.151 6.6

1.300 6.6 0.149 0.0

15 1.448 6.9

1.223 6.8 -0.225 -0.1

16 1.385 5.8

1.321 5.9 -0.064 0.1

17 1.501 6.7

1.516 6.5 0.015 -0.2

18 1.560 6.8

1.467 7.6 -0.093 0.8

R²=0,71

0,8

1,0

1,2

1,4

1,6

1,8

2,0

0,8 1,0 1,2 1,4 1,6 1,8 2,0

Figure 3: Correlation between experimental data and

simulated data (neural network output) for kerf.

MODELING OF ABRASIVE WATER JET MACHINING USING TAGUCHI METHOD AND ARTIFICIAL NEURAL

NETWORKS

379

R²=0,70

4,0

5,0

6,0

7,0

8,0

9,0

10,0

4,0 5,0 6,0 7,0 8,0 9,0 10,0

Figure 4: Correlation between experimental data and

simulated data (neural network output) for R

5 CONCLUSIONS

The proposed hybrid approach based on Artificial

Neural Networks and Taguchi methodology was

used for AWJM mean kerf width and surface

roughness modelling purpose.

The Taguchi approach was used in order to

optimize the experimental effort whitout loosing the

prediction accuracy of the ANN model.

The acquired results indicate that the proposed

modelling approach could be effectively used to

predict the kerf geometry and the surface roughness

in AWJM, thus supporting the decision making

during process planning.

ACKNOWLEDGEMENTS

The authors wish to thank Sielman S.A., Volos,

Greece, for AWJM of the specimens. TRIP steels

were provided by Laboratory of Materials, Dept. of

Mechanical Engineering, University of Thessaly.

REFERENCES

Wang, J. & Wong, W. (1999). Study of abrasive waterjet

cutting of metallic coated sheet steels. International

Journal of Machine Tools & Manufacture, 39, pp. 855-

870.

Demuth, H. & Beale, M. (2001). Neural networks toolbox

for use with Matlab, User’s guide. The MathWorks,

Inc.

Gudimetla, P., Wang, J. & Wong, W. (2002). Kerf

formation analysis in the abrasive waterjet cutting of

industrial ceramics. Journal of Materials Processing

Technology, 128 (1-3), pp. 123-129.

Hascalik, A., Ulas, C. & Gurun, H. (2007). Effect of

traverse speed on abrasive waterjet machining of Ti-

6Al-4V alloy. Materials & Design, 28(6), pp. 1953-

1957.

Jegaraj, J. J. R. & Babu, N. R. (2007). A soft computing

approach for controlling the quality of cut with

abrasive waterjet cutting system experiencing orifice

and focusing tube wear. Journal of Materials

Processing Technology , 185 (1-3), pp. 217-227.

Kechagias, J. (2007). Investigation of LOM process

quality using design of experiments approach. Rapid

Prototyping Journal, 13(5), 316-323.

Kechagias, J., Pappas, M., Karagiannis, S., Petropoulos,

G., Iakovakis, V. & Maropoulos, S. (2010). An ANN

approach on the optimization of the cutting parameters

during CNC plasma-arc cutting. In: Proceedings of

ESDA2010: 10

Biennial ASME Conference on

Engineering Systems Design and Analysis, 12-14 July

2010, Istanbul, Turkey.

Momber, A. W. & Kovacevic, R. (1997). Principles of

Abrasive Water Jet Machining. Springer.

Olson, G. B. & Azrin, M. (1978). Transformation behavior

of TRIP steels. Metallurgical and Materials

Transactions A, 9(5), pp. 713-721.

Pappas, M., Kechagias, J., Iakovakis, V. & Maropoulos, S.

(2011). Surface roughness modelling and optimization

in CNC end milling using Taguchi design and Neural

Networks. In: Proceedings of the 3rd International

Conference on Agents and Artificial Intelligence, pp,

595-598.

Petropoulos, G., Tsolakis, N.; Vaxevanidis, N. &

Antoniadis, A. (2009) Topographic description of

abrasive waterjet machined surfaces. In: Proc. 2

European Conference on Tribology -ECOTRIB 2009,

7-10 June 2009, Pisa, Italy, pp. 309-314.

Valicek, J. et al. (2007). Experimental analysis of

irregularities of metallic surfaces generated by

abrasive waterjet. International Journal of Machine

Tools & Manufacture, 47(11), pp. 1786-1790.

Vaxevanidis, N. M., Markopoulos A. & Petropoulos G.

(2010). Artificial Neural Network Modeling of

Surface Quality Characteristics in Abrasive Water Jet

Machining of Trip Steel Sheet. In: J.P. Davim (ed.)

Artificial Intelligence in Manufacturing Research.

Nova Science Publishers, Inc, pp 79-99.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

380