NEIGHBORHOOD FUNCTION DESIGN FOR EMBEDDING IN

REDUCED DIMENSION

Jiun-Wei Liou and Cheng-Yuan Liou

Department of Computer Science and Information Engineering, National Taiwan University, Taipei, Taiwan

Keywords:

Dimension reduction, Local linear embedding, K-nearest neighbors, Epsilon distance.

Abstract:

LLE(Local linear embedding) is a widely used approach for dimension reduction. The neighborhood selection

is an important issue for LLE. In this paper, the ε-distance approach and a slightly modiﬁed version of k-nn

method are introduced. For different types of datasets, different approaches are needed in order to enjoy higher

chance to obtain better representation. For some datasets with complex structure, the proposed ε-distance

approach can obtain better representations. Different neighborhood selection approaches will be compared by

applying them to different kinds of datasets.

1 INTRODUCTION

LLE(Roweis and Saul, 2000) is a well known ap-

proach for showing the structure of high dimensional

data within low dimentional embeddings. The ﬁrst

step of LLE algorithm is to ﬁnd out the neighborhoods

of every points. Traditionally, the k-nearest neighbor

approach is the most widely used one. This approach

has many advantages such as easy to implement, suit-

able for most of cases when the distribution of the

dataset is uniform enough and have no complex struc-

tures, fast enough and can be parallelized and further

accelerated (Yeh et al., 2010).

But for some other type of dataset, the k-nn ap-

proach will face difﬁculty since the number of se-

lected nearest neighbors can only be a ﬁxed integer

over full dataset, the possible LLE embedding will be

limited if the dataset is not very large, but contains

complex structure. If k is small, the structure is hard

to extract, while for large k, the complex structure

may be destroyed because of generating errornous

connections from one possible sub-structure to an-

other. Also, for non-uniform sampling, the selection

of k may also be a problem. For these kind of prob-

lems, the ε-distance approach is suggested for attempt

to get better embeddings.

Although there are already attempts for modifying

neighborhood functions, such as weighted neighbor-

hood (Chang and Yeung, 2006; Pan et al., 2009; Wen

et al., 2009; Zuo et al., 2008), clustering approaches

(Wen et al., 2006), or including k-means (Wei et al.,

2010; Wen et al., 2006). But these modiﬁed ap-

proaches are mostly analyzed and based on original

k-nn method only. In this paper, the ε-distance will be

taken into main consideration as a different concep-

tual method from k-nn for trying to deal with more

complex datasets.

Since the neighborhood selection approach is

changed, following the original LLE algorithm, the

weight computation is not affected signiﬁcantly,

while the minimum eigenvalue ﬁnding needs some

modiﬁcation since the neighborhood selection is no

more balanced across all points, the matrix is more

likely to hold more zero eigenvalues so that the origi-

nal way of ﬁnding smallest eigenvalue may not work

properly. The further modiﬁcation details for ﬁnding

minimal eigenvalues will be discussed later.

The rest of the paper is organized as following:

In section 2, the detail of ε-distance approach will be

introduced. In section 3, the experiments on different

sets of data will be discussed. Before the experiments,

some more details and minor modiﬁcations for LLE

will be addressed. In section 4 is the ﬁnal thought

about the comparison.

2 METHOD

2.1 Neighborhood Selection

In this paper, we focus on the nearest neighbor ap-

proaches using in LLE. The original approach used in

LLE is k-nearest neighbors, which just look into full

190

Liou J. and Liou C..

NEIGHBORHOOD FUNCTION DESIGN FOR EMBEDDING IN REDUCED DIMENSION.

DOI: 10.5220/0003681201900195

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 190-195

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

−0.5 0 0.5

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

Figure 1: Example for 8-nn selection.

−0.5 0 0.5

−0.5

−0.4

−0.3

−0.2

−0.1

0.1

0.2

0.3

0.4

0.5

Figure 2: Example for selection within radius ε =

√

0.05.

data and ﬁnd out k nearest points from each point as

its neighbors.

For the ε-distance approach, a point is a neighbor

of a certain point p if the distance from the point to p

is no more than a preset distance ε. Example neigh-

borhood selection from 8-nn can be shown in Fig-

ure 1, while neighborhood selection from ε-distance

within radius ε =

√

0.05 can be shown in Figure 2.

2.2 Regularization

After the neighborhood selection, a process for com-

puting neighborhood weights are performed. When

the number of nearest neighbor selected is larger than

the data dimension, the regularization should be taken

into account, and the regularization parameter and

strategy will have signiﬁcant impact on the ﬁnal LLE

embedding result (Daza-Santacoloma et al., 2010).

In this paper, the regularization method for each ap-

proach is equivalent to the orginal LLE implementa-

tion in order to have better focus on effects of dif-

ferent neighborhood selection approaches. The reg-

ularization parameter using by the original LLE im-

plementation is 10

−3

, but for the ε-distance approach,

the regularization parameter can be manually tuned.

2.3 Minimal Eigenvalues

After the neighborhood weight vectors {w} are com-

puted, the last step for LLE is to compute the d small-

est eigenvalue of the matrix M = (I −W)

′

(I −W).

d means the ﬁnal embedding number of dimensions,

and W means the collection from all weight vectors

Since the ε-distance method will not generate bal-

anced number of neighbors such as k-nn does, the ma-

trix M generated from ε-distance method is expected

to have worse condition than the matrix from k-nn.

Since LLE needs d smallest eigenvalues which are

not zero, and the precision of computer number is al-

ways limited, the original eigenvalue searching mech-

anism for k-nn which directly search nearest to the

true zero eigenvalues will encounter problem if we

apply it directly on the ε-distance method. Because

machine precision is limited, the matrix M originally

should be stated as at least positive semi-deﬁnite, so

that the eigenvalues of M should be larger than or

equal to zero. But when it comes to computing eigen-

decomposition, we can only obtain the corresponding

eigenvalues as between some negative machine ep-

silon and positive machine epsilon instead of some

true zeros. So the proposed modiﬁcation is using the

original eigenvalues searching program to guess the

smallest eigenvalue signiﬁcantly larger than machine

epsilon and then ﬁnd d smallest eigenvalues near to

the smallest eigenvalue.

For the initial guess of the smallest eigenvalue,

since directly ﬁnding the eigenvalues nearest to 0 per-

forms well on k-nn approach and the modiﬁed k-nn,

so the initial guess for the two methods will remain

0. For ε-distance approach, this parameter can be set

and the program will try to ﬁnd the possible smallest

eigenvalueby multiplying with a factor of 1.5 for each

step from the initial guess of the smallest eigenvalue

which should be larger than machine epsilon.

3 EXPERIMENT

Before performing experiments, there are some is-

sues other than the focused neighborhood selection

approaches should be considered.

3.1 K-nn Modiﬁcation

Commonly, the k in the k-nn method should be inte-

ger, but this restriction is too strong so that the number

NEIGHBORHOOD FUNCTION DESIGN FOR EMBEDDING IN REDUCED DIMENSION

191

of possible embeddings can be generated from k-nn

is heavily limited. For resolving this issue, a simple

modiﬁcation for fractional k-nn is to perform original

k-nearest neighbor and insert one more neighbor for

some certain points which havenearest k+1-th neigh-

bor. By this modiﬁcation, we can generate much more

possible embeddings from the modiﬁed k-nn method.

If the best result of the method is considered as still

not good enough, the problem will be mostly in the k-

nn selection approach instead of insufﬁcient number

of conﬁgurations caused by the integer constraint of

3.2 Parameters

The parameters can be separated as regularization pa-

rameters, eigenvalue solving parameters, and k-nn or

ε-distance parameters. The regularization term us-

ing in the LLE algorithm are set to equal for all dif-

ferent neighborhood selection methods. The regular-

ization parameter can be tuned in the ε-distance ap-

proach since the numbers of connections are differ-

ent for each point, while the k-nn and modiﬁed k-

nn use the default parameters in the original source.

Other parameters such as the number of neighbors for

k-nn, the radius and corresponding parameters for ε-

distance are determined by grid search.

3.3 Datasets

There are several artiﬁcially created datasets to test

the ability of different approaches. The ﬁrst dataset

is started from the swiss roll dataset to ensure the us-

ability of each approach. The swiss roll dataset con-

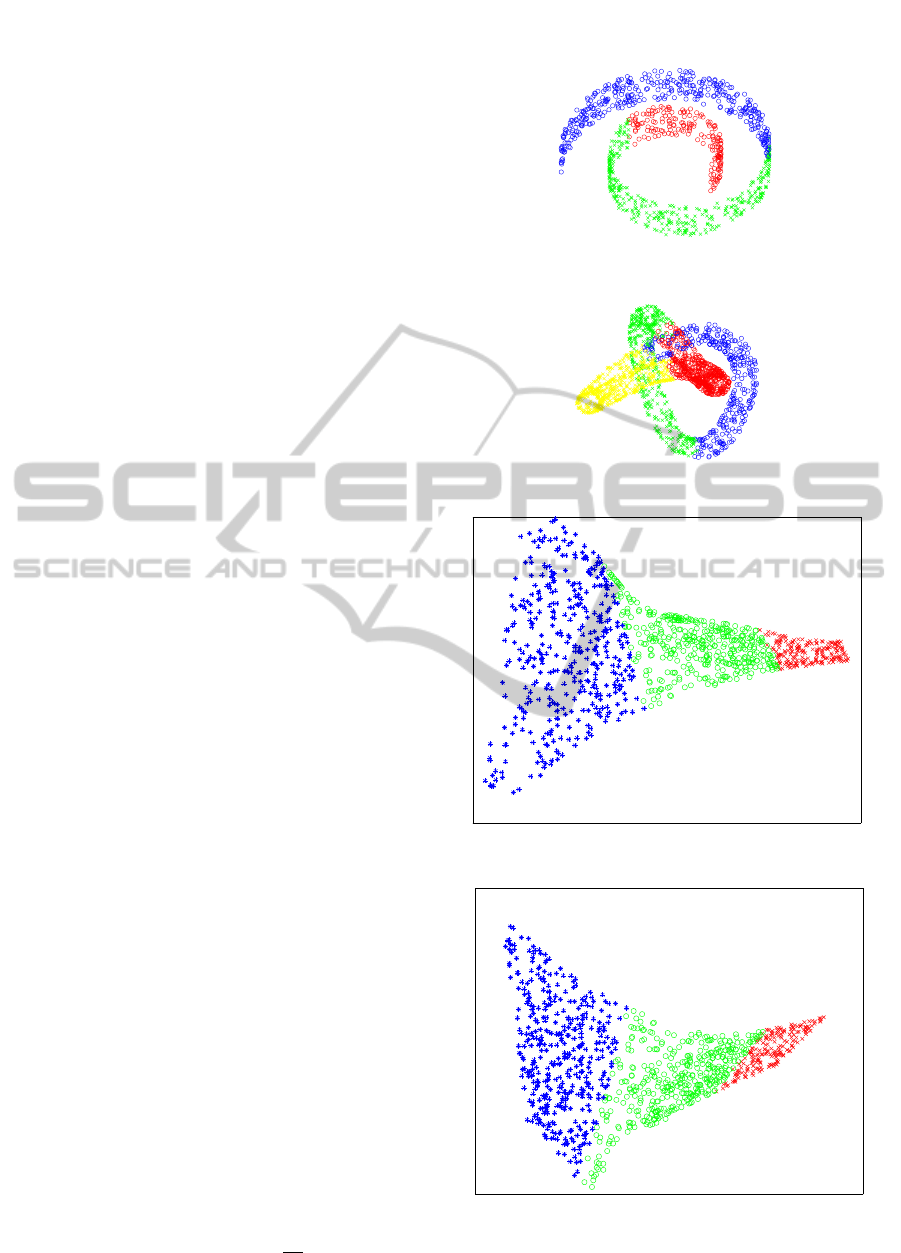
tains 1000 points as in Figure 3. The second dataset

is a dataset with a knot structure with 2000 points

distributed non-uniformly as in Figure 4. The third

dataset is a database of gray-level face images for the

same person with different angles and moods which

can be considered as true data. The number of images

is 1965 and the resolution of images is 28x20.

3.4 Result

For the swiss roll dataset, the 7-nn, and 8-nn result

can be shown in Figure 5 and 6. So using the integer

number of k-nn cannot really extract the swiss roll to

ﬁll the embedding plane since the even higher k will

map the swiss roll to an unseparable plane. With 7-nn

plus 500 next nearest neighbors, the result is as Figure

7, which expands data more to ﬁll the plane. For the

ε-distance approach, the radius ε =

√

21, with the reg-

ularization parameter 10

−3

, and the initial minimum

solution guessing is 10

−14

. The result can be shown in

Figure 3: The swiss roll dataset.

Figure 4: The knot dataset.

Figure 5: The 7-nn embedding result for swiss roll.

Figure 6: The 8-nn embedding result for swiss roll.

Figure 8. The two proposed modiﬁcations have bet-

ter chance to ﬁnd proper embedding surface for swiss

roll dataset.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

192

Figure 7: The fractional nearest neighbors embedding result

for swiss roll.

Figure 8: The ε-distance embedding result for swiss roll.

For the knot dataset, the best embedding result for

k-nn is 7-nn, the correspondingresult can be shown in

Figure 9. For this result, the original one tube struc-

ture is successfully extracted. For the fractional near-

est neighbors, the best selection for representation is

6-nn plus 1700 next nearest neighbors, the result can

be shown in Figure 10. Although the structure is a lit-

tle bit fractured, but the big structure is not collapsed,

and the representation is clearer than the 7-nn result.

For the ε-distance approach, the best result is for ra-

dius ε =

√

0.39, with regularization parameter equal

to 0.001, and the initial guess for minimum eigen-

value is 4×10

−14

. The result can be shown in Figure

11, which is similar to the fractional nearest neigh-

bors’ result. All methods can extract the one tube

structure from the original knots, but the represen-

tation for fractional nearest neighbors and ε-distance

approach are considered as better than only using k-

nn.

For the face dataset, the 12-nn template for k-nn

approach can be shown in Figure 12. The regular-

Figure 9: The 7-nn embedding result for knot.

Figure 10: The fractional nearest neighbors embedding re-

sult for knot.

Figure 11: The ε-distance embedding result for knot.

ization parameters for different LLE methods are all

zeros since the data dimension 560 should be much

larger than the number of neighbors needed for em-

beddings. For the fractional k-nn approach, the re-

sult for 12-nn plus 327 more nearest neighbors can be

NEIGHBORHOOD FUNCTION DESIGN FOR EMBEDDING IN REDUCED DIMENSION

193

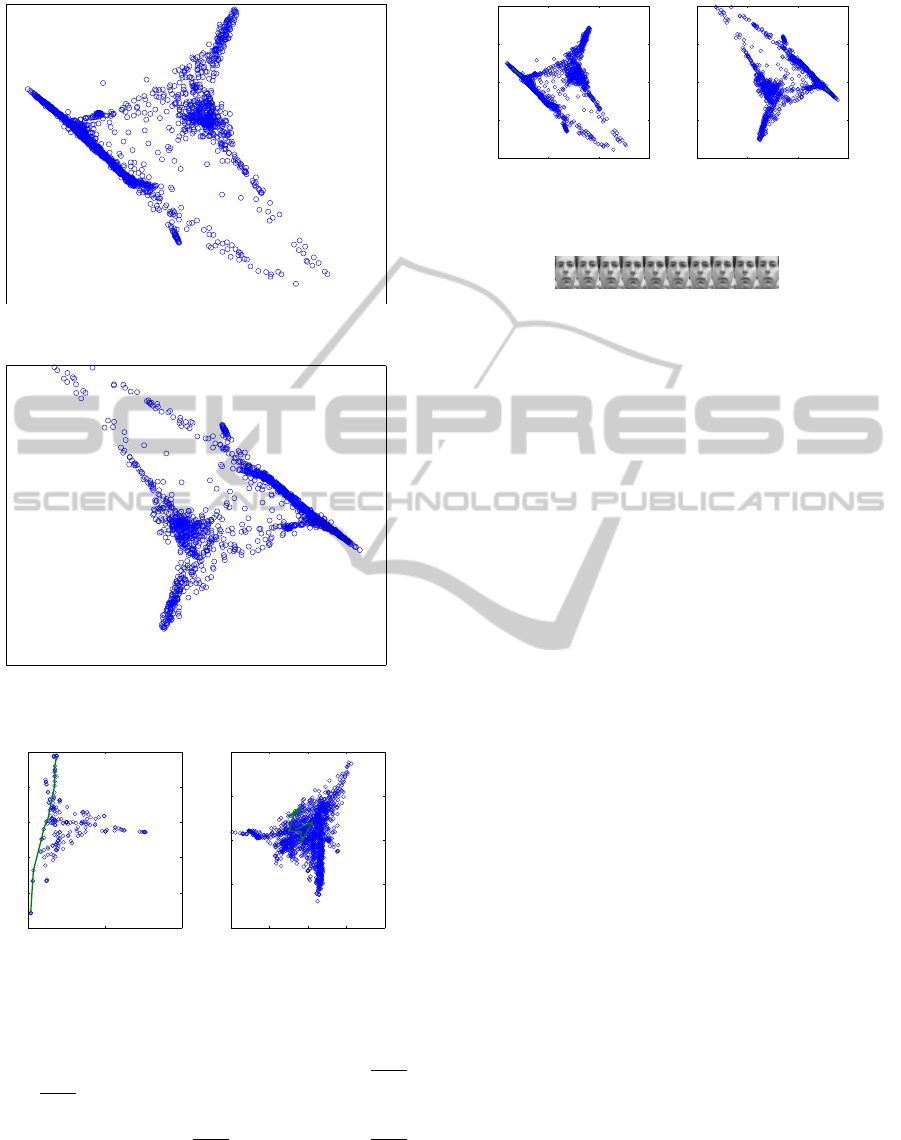
Figure 12: The 12-nn embedding result for face dataset.

Figure 13: The fractional nearest neighbors embedding re-

sult for face dataset.

−5 5 15

−12

−8

−4

−4 −2 0 2 4

−4

−2

Figure 14: The ε-distance embedding result for face dataset.

shown in Figure 13. The ε-distance method encoun-

tered difﬁculties because nearest neighbors of some

points are still very far away in comparison of direct

distance from pixel to pixel. The radius ε =

√

1.05,

ε =

√

3.45, with initial guess 10

−14

can be shown

in Figure 14. The numbers of removed isolated data

points are 1024 for ε =

√

1.05 and 89 for ε =

√

3.45.

The corresponding green line in the ﬁgure indicates

a path for a reference face translation as in Figure 16.

The correspondinggreen line on the original and frac-

tional k-nn embedding can be shown in Figure 15.

−2 0 2 4

−4

−2

−4 −2 0 2

−4

−2

Figure 15: The reference face translation for ε-distance em-

bedding.

Figure 16: The reference face translation for ε-distance em-

bedding.

4 CONCLUSIONS

From results shown above, we know that for differ-

ent dataset, using different approaches obtain slightly

different representation results. k-nn is not always

the best for analyzing neighborhoods. The proposed

ε-distance approach may extract the structure better

than k-nn if we really do not have many data sam-

ples, but the data shown complex structures. For the

fractional nearest neighbors, the increasing number of

choices for embedding conﬁguration can also help for

ﬁnding better embedding representations of the data.

So the two approaches can be used for alternative of

the conventional k-nn to have more ways to ﬁnd out

the hidden data structure.

REFERENCES

Chang, H. and Yeung, D.-Y. (2006). Robust locally linear

embedding. Pattern Recognition, 39:1053–1065.

Daza-Santacoloma, G., Acosta-Medina, C. D., and G., C.-

D. (2010). Regularization parameter choice in locally

linear embedding. Neurocomputing, 73:1595–1605.

Pan, Y., Ge, S. S., and Mamun, A. A. (2009). Weighted lo-

cally linear embedding for dimension reduction. Pat-

tern Recognition, 42:798–811.

Roweis, S. T. and Saul, L. K. (2000). Nonlinear dimension-

ality reduction by locally linear embedding. Science,

290(5500):2323–2326.

Wei, L., Zeng, W., and Wang, H. (2010). K-means clus-

tering with manifold. In 2010 Seventh International

Conference on Fuzzy Systems and Knowledge Discov-

ery, pages 2095–2099. IEEE Xplore Digital Library

and EI Compendex.

Wen, G., Jiang, L., and Wen, J. (2009). Local relative trans-

formation with application to isometric embedding.

Pattern Recognition Letters, 30:203–211.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

194

Wen, G., Jiang, L., Wen, J., and Shadbolt, N. R. (2006).

Clustering-based nonlinear dimensionality reduction

on manifold. In PRICAI’06 Proceedings of the 9th

Paciﬁc Rim international conference on Artiﬁcial in-

telligence, pages 444–453. Springer-Verlag.

Yeh, T., Chen, T.-Y., Chen, Y.-C., and Shih, W.-K. (2010).

Efﬁcient parallel algorithm for nonlinear dimension-

ality reduction on gpu. In 2010 IEEE International

Conference on Granular Computing, pages 592–597.

IEEE Computer Society.

Zuo, W., Zhang, D., and Wang, K. (2008). On kernel

difference-weighted k-nearest neighbor classiﬁcation.

Pattern Analysis and Applications, 11:247–257.

NEIGHBORHOOD FUNCTION DESIGN FOR EMBEDDING IN REDUCED DIMENSION

195