
A NEW DISTRIBUTION SYSTEM RECONFIGURATION
APPROACH USING PARTICLE SWARM OPTIMIZATION
AND NEURAL NETWORK
M. W. Siti, B. P. Numbi, J. Jordaan and D. Nicolae
Department of Electrical Engineering, Tshwane Univeristy of Technology, 0001, Pretoria, South Africa
Keywords: Network reconfiguration, Mixed-integer programming, Binary particle swarm optimization, Neural
network.
Abstract: This paper uses artificial intelligent algorithms for reconfiguration of the distribution network. The problem
is formulated as an optimization problem where the objective function to be minimized is the power losses,
and the constraints are nodal voltage magnitude limits, branch current limits, Kirchhoff’s current law
(KCL), Kirchhoff’s voltage law (KVL) and the network radiality condition. While the state (on-off) of the
tie switch is considered as control or independent variable, the nodal voltage magnitude, branch current are
considered as state or dependent variables. These state variables are continuous whilst the switch state is an
integer (binary) variable. The problem being a mixed-integer programming one because of the state of
switch (on=closed=1 or off=open=0), a Binary Particle Swarm Optimization (BPSO) and Neural Network
are used separately to solve this problem. The effectiveness of proposed method is demonstrated through an
example.
1 INTRODUCTION
The energy in the system is wasted in the form of
power losses at the distribution level. Recent
advances in distribution automation technology have
made it possible to reduce these losses by applying
loss minimization techniques on a real time basis.
At the HV and MV levels, the load is usually
three-phase and balanced, although large single or
dual phase loads can be connected. Each feeder in a
distribution system usually supplies a mix of
residential, commercial and sometimes industrial
consumers with varying needs depending on the
season of the year (Chen and Cherng, 2000); (Liu et
al., 1989). Because of load changes and the diversity
of loads being on or off, the three phase imbalances
may be substantial. Balancing is accomplished by
selecting the phase of the supply for each load so
that the total load is distributed as evenly as possible
between the phases for each section of the feeder.
The balancing procedure must consider all possible
combinations of phase loads connecting to three
phases. There are a number of benefits that make
efficient load phase balancing a worthwhile
objective. Balancing reduces feeder losses for the
phases as the square of the current magnitude.
Loading on a feeder section is synonymous with the
most heavily loaded phase so that, in the case of
significant imbalance, feeder capacity is used
inefficiently. Balancing between phases tends to
equalize the phase loading by reducing the largest
phase peak load while increasing the load on the
other phases. This equates to releasing feeder
capacity that can be used for future load increases
without reinforcing feeder conductors. Released
feeder capacity provides more reserve loading
capacity for emergency loading conditions.
Balancing not only reduces feeder losses, but
also improves voltage on a feeder by equalizing the
voltage drops in each phase along the feeder. It is
realistic to assume that the benefits in improved use
of feeder capacity and voltage quality are significant
in terms of the value of reduction in loss except
when loading is already high (Ukil et al., 2006).
In past, many studies based on traditional
heuristic algorithms have been carried out on
network and feeder (Zhu, 2009); (Alexandre et al.,
2009). The problems were formulated and solved to
control the switching of sectionalize and tie switches
so as to achieve a better efficiency. However, they
218
W. Siti M., P. Numbi B. and Nicolae D..
A NEW DISTRIBUTION SYSTEM RECONFIGURATION APPROACH USING PARTICLE SWARM OPTIMIZATION AND NEURAL NETWORK.
DOI: 10.5220/0003681902180223
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 218-223
ISBN: 978-989-8425-84-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

did not guarantee the optimal solution although they
provide high quality suboptimal solution.
Recently new methods based artificial intelligent
such as genetic algorithm (GA) have been used in
the distribution network reconfiguration (Zhu,
2009). However, it has been shown in general that
PSO algorithm can provide better optimal solution
than GA (Zhu, 2009); (Yu et al., 2009) and it is also
requires lower computational time than GA (Zhu,
2009).
From the above background, the authors in this
paper have used a Binary particle swarm
optimization (BPSO) algorithm for the distribution
network reconfiguration loss minimization. Neural
network algorithm is used also in order to validate
the results obtained by BPSO algorithm.
2 PROBLEM DESCRIPTION AND
FORMULATION
2.1 Network Reconfiguration
The distribution system is the final stage in the
transfer of power to individual customers. Typically,
it commences from the sub transmission station
transformers, and normally will consist of two levels
primary distribution or medium voltage level
(Alexandre et al., 2009); (Siti et al., 2007).
There are two types of switch in primary
distribution systems: normally closed switch
connects line sections, and normally open switch on
the tie-lines which connects two primary feeders, or
two substation or loop-type laterals. Network
reconfiguration (or feeder reconfiguration) is the
process of altering the topological structures of the
distribution feeders by changing the open /closed
status of the sectionalizing and tie switches
(Alexandre et al., 2009), (Siti et al., 2007).
In general, distribution loads shows different
characteristics according to their corresponding
distribution lines and line sections. Therefore, load
levels for each time period can be regarded as non
identical. In the case of a distribution system with
some overloaded to less loaded feeders. The
maximum current which the feeder conductor can
take may be considered as the reference.
Nevertheless, the transfer of load must be such that
certain predefined objective is satisfied. In this case,
the objective is to ensure the network has minimum
real power loss.
The solution objective for a feeder is to obtain a
set of rearrangement of the connected loads at each
node (or consumer point) such that the objective
function is minimized. This is a non-linear problem
that will involve a number of trial and errors. It is
hereby proposed to solve this problem, where
iteratively, as changes are made, a method is used to
sense the relative loading of the phases, and another
method is used to edge towards the minimized
objective.
2.2 Mathematical Model for Optimal
Network Reconfiguration
This mathematical model has been discussed in
(Zhu, 2009); (Alexandre et al., 2009), (Siti et al.,
2007).The objective function to be minimized is the
total active power losses and is expressed in terms of
branch current as given below:
Min
NB
l
bbbL
IRkP
1
2
NBb
(1)
where
L
P
,
b
k
,
b
R
,
b
I
and
NB
are respectively, the
total active power losses, the tie switch state of the
branch
b
(
1
b
k
if branch
b
is closed and
0
b
k
if
branch
b
is open), resistance and current magnitude
of the branch
b
, and
NB
is the total number of
branches.
The operating constraints of the network are
given as follows:
2.2.1 Inequality Constraints
These constraints are nodal voltage and branch
current limits.
0.95 . . 1.05 . .
i
p
uV pu££
(2)
max
bbb
IIk
(3)
where
i
V
is the voltage magnitude at node
i
,
max
b
I
(1.pu. in this paper) is the maximum branch current.
2.2.2 Equality Constraints
The fists equality constraint is the Kirchhoff’s
current law (KCL), given as follows:
()
,0
i
hIb= iNÎ
(4)
The second equality constraint to be satisfied is the
Kirchhoff’s voltage law (KVL), given as follows:
()
,0
i
hVb=
iNÎ
(5)
A NEW DISTRIBUTION SYSTEM RECONFIGURATION APPROACH USING PARTICLE SWARM
OPTIMIZATION AND NEURAL NETWORK
219

Another equality constraint is the one that ensure the
radiality condition of the network. This means that
the number of branches in the network must be
smaller than the number of nodes by one unit (
1 NNBk
b
) (Zhu, 2009). This can be expressed
by the following equation:
0
b
k
(6)
Any text or material outside the aforementioned
margins will not be printed.
2.3 Feeder Test System
In this case the suggestion is that the 66 kV be fed at
both ends instead of at one end only, since the total
voltage drop can be considerably reduced without
increasing the cross section of the conductor, and
also taking into account that the ends of distribution
are supplied with equal voltage. The system
distribution can be fed at both ends with the equal
voltage. Let S represent the sectionalizing switch
and T represent the tie switch as shown in Figure 1.
Figure 1: Network representation.
3 PROPOSED METHODS
3.1 Classical PSO
Particle swarm optimization is an intelligent
algorithm developed by Kennedy and Eberhart in
1995 as an alternative to genetic algorithm (GA)
(Zhu, 2009). The PSO algorithm motivation was the
social behaviour such as bird flocking and fish
schooling. This algorithm was used to solve many
nonlinear hard optimization problems (Zaraki and
Othman, 2009). The main advantage of the PSO
over traditional optimization algorithm is the fact it
does not need any gradient information about the
objective function when search for the global
optimal solution (Zhu, 2009); (Zaraki and Othman,
2009). Another advantage is the fact that it less
dependent on the initial starting point in the search
space (Numbi et al., 2011). Over other intelligent
algorithms such as GA, PSO can be easier to
program, to modify, inexpensive in terms of memory
and even computation time, etc. (Zhu, 2009);
(Mantawy and Al-Ghamdi, 2003). The general PSO
algorithm for real-valued numbers is explained as
follows:
From an initial position, a swarm of particles
starts flying in the search space exploring optimal
points. Each particle position represents a potential
solution. Therefore, the performance of each particle
position is evaluated by the fitness function which is
the objective function in this work. Our problem
having minimization purpose, the best particle is the
one with lower fitness value. During the flight
(iterations), the best experiences (positions) for each
particle is stored in its memory and called personal
best (Pbest). The lowest value of all the Pbests,
determines the global best (Gbest) of the swarm.
The velocity and the position of each particle are
updated using respectively, the following equations:
()
()
1
11
22
t t pbest t
ii ii
Gbest t
ii
VwVCrX X
Cr X X
+
=+ -+
-
(7)
11
t
i
t
i
t
i
VXX
(8)
with
w
: The Inertia weight (0.729 for clerc’s constriction
method) (Eberhart and Yuhui, 2001)
C
1
, C
2
: Acceleration coefficients (1.49445 for clerc’s
constriction method) (Eberhart and Yuhui, 2001)
r
1
, r
2
: Two separately generated uniformly
distributed random numbers in the range [0, 1]
added in the model to introduce stochastic nature.
3.1.1 Proposed Fitness of the Binary Particle
Swarm Optimization (BPSO)
With the purpose of dealing with constraints, all the
constraints given by (2)-(6) are penalized in the
main objective function given by (1). Exterior
penalty terms are used here. Since our problem has
binary control variables which are the states of tie
switch (on=1 or off=0), these tie switch states are
treated first as continuous number (real-valued
number) between 0 and 1. Secondly, the conversion
of continuous number to binary number is done as
follows:
-if the value of the particle position (tie switch state)
is less than 0.5 then this is set to zero,
-if the value of the particle position is greater than
0.5 then this set to one,
TT
T
TT
1
I
2
I
3
I
5
I
4
I
6
I
5
S
4
S
3
S
2
S
1
S
6
S
NCTA 2011 - International Conference on Neural Computation Theory and Applications
220
-otherwise, the PSO is reinitialized.
Therefore, the fitness of each particle in the swarm
is given as a penalty functions as expressed below:
()
()
{}
()
{}
()
{}
2
2 max
1
1
2
2
min max
1 2
1 1
max 0,
max 0, max 0,
NB
ibbb bb
b
NB N
bb ii
b i
FX kRI k k
kk VV
m
mm
=
= =
=+ - +
-+ - +
å
åå
()
{}
()
{}
2
2
min max
23
11
max 0, max 0,
NNB
ii bbb
ib
VV kIImm
==
-+ - +
åå
(){} (){}
22
44
11
,,
NN
ii
hIk hVkmm
==
+
åå
(9)
with
41
....
the penalty factors or coefficients for each
constraint violations. In order to reduce the number
of these penalty factors, all of them have been set to
a value of 10000.
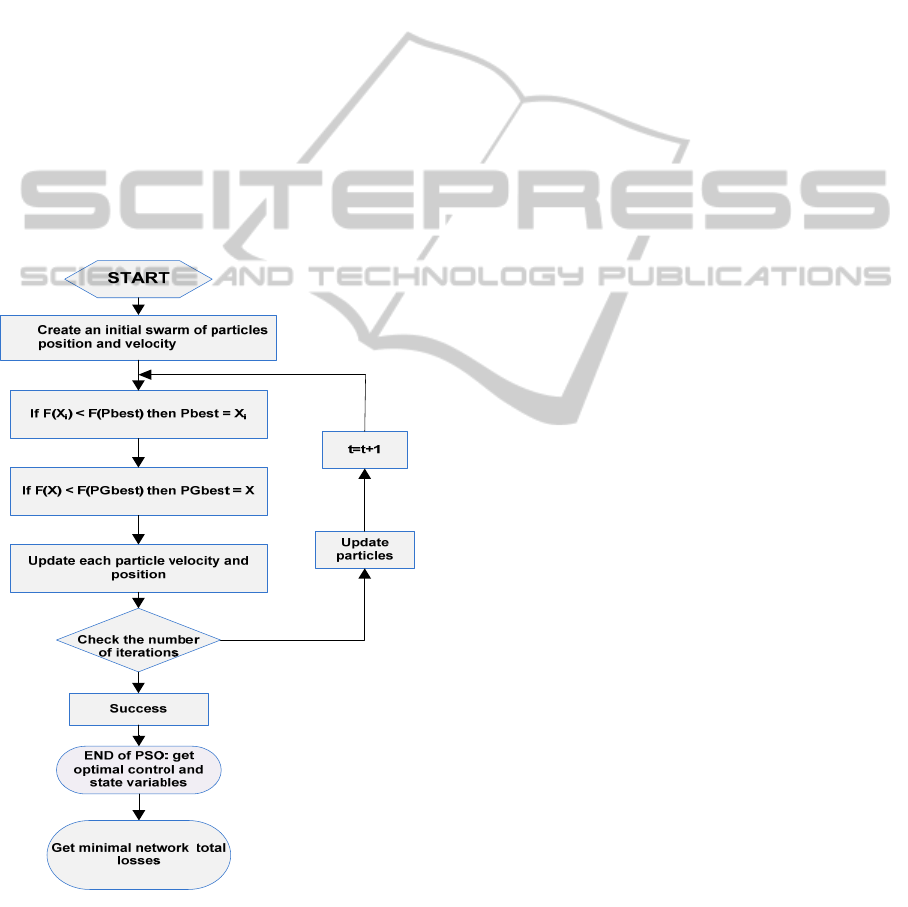
The flowchart of BPSO is shown in figure 2
given below:
Figure 2: Flowchart of PSO algorithm.
3.2 Neural Networks
In the proposed strategy in this paper, the neural
network must control the switch-closing sequence of
each branch to achieve the minimum power loss
which will lead to the distribution network
reconfiguration. The inputs to the neural network are
the unbalanced branch currents while the outputs are
the switch closing sequences for each node.
The input layer of the network contains N input
neurons, N being the number of unbalanced branch
currents to be controlled. The following column
vector has been assumed as the input:
T
bNbSW
IIC .................
1
(10)
The output of the network is in the range {0,1} for
each switch, i.e., indicating which switch must be
open or close to reduce the power loss in the
network.
3.2.1 Neural Network Structure
For this application, we used the radial basis
network. Experiments with the back propagation and
the radial basis networks indicated faster training
and better convergence for the latter. Radial basis
networks may require more neurons than the
standard feed-forward back propagation networks,
but often they can be designed in a fraction of the
time needed to train the standard feed-forward
networks. They work best when many training
vectors are available. The Matlab
®
neural network
toolbox (Math Works; release 13) has been used for
the implementation. We experimented with different
kinds of radial basis networks, but a generalized
regression neural network (GRNN) produced the
best result (Ukil et al., 2006). Such a network is
often used for function approximation. It consists of
a radial basis layer and a special linear layer (Ukil et
al., 2006).
3.2.2 Neural Network Training
We have used the neural network-based operation
for the test data in the following structure: real and
simulated data for network presented in figure 1.
The real data set consisted of unbalanced network.
The test data set contained average load current
values per load in a specific network of the country
for the different times of each day in a month. We
selected a specific network as our test data for each
specific time, and we tested our result on 500 sets of
data. We consider the loads to be equally distributed
per phase, that is, we assume that the load flow
distribution in a loop is an optimal flow; the
corresponding network power losses will be
minimal. Thus the basic idea of the optimal flow
A NEW DISTRIBUTION SYSTEM RECONFIGURATION APPROACH USING PARTICLE SWARM
OPTIMIZATION AND NEURAL NETWORK
221

pattern is to open the switch of the branch that has
minimal current value in loop, with the optimal flow
pattern were to compute load flow of initial radial
network, it will follow by the closing of all normal
switches to produce loop networks, this will
continue by computing the equivalent injection
current at all nodes in loops through injecting
current method, and the replacement of the branch
impedance by corresponding branch resistance in the
loop and then compute the optimal flow, the network
will have a new reconfiguration by opening a switch
branch that has a minimal current value in loop. And
can again recomputed the load flow for the remained
network, this will end by opening the next branch
switch, and repeat the previous step discussed above,
until we have the radial network.
4 RESULTS AND DISCUSSION
The following case illustrates the loss reduction
through network reconfiguration of the tested system
of a 6 bus radial distribution. To evaluate the
proposed techniques, it has been applied to 6 bus
radial distribution system loss reduction. The results
obtained from the combination PSO, and as been
validated by Neural Network with the control of the
tie switch, it shows that it succeed in finding the
global solution with a high probability in the system
as represented in table 1
Table 1: Results of 6 bus radial distribution network
reconfiguration.
Description Initial State PSO
Neural
Network
Tie Switch open Switch 1-2 Switch 3-2
Switch 3-5
Switch 3-2
Switch 3-5
Total
Power
Loss
(MW)
Best ------------- 0.0096525 0.009652
Average ---------- 0.00117044 0.00117044
Worst 0.0095452 0.0035428 0.0035428
Average Power Loss
Reduction (%)
62.23 62.23
Minimum Voltage
Magnitude (p.u.)
0.894 0.978 0.978
5 CONCLUSIONS
Loss reduction is very important complement to
network and feeder reconfiguration. In this paper the
network and feeder reconfiguration problem was
formulated as loss minimization problem with the
view for its solution to control different switches
placed in the network. Two MATLAB based
solution methods have been proposed and
demonstrated. First is the PSO and the other is
neural network-base technique. The proposed
methods were successfully tested. From the practical
point of view these method can be very effective as
several model based approaches usually take very
long running time. The PSO has been found more
suitable and faster compared to neural network. But
both methods gives good results on loss reduction in
the network.
REFERENCES
T. H. Chen and J. T. Cherng, "Optimal Phase
Arrangement of Distribution Transformers Connected
to a Primary Feeder for System Unbalance
Improvement and Loss Reduction Using Genetic
Algorithm," IEEE Trans. Power systems, vol. 15,
August, 2000.
C. C. Liu, S. J. Lee, and K. Vu, "Loss Minimization of
Distribution Feeders: Optimality and Algorithms,"
IEEE Trans. Power delivery, vol. 4, April, 1989.
A. Ukil, M. Siti, and J. Jordaan, "Feeder Load Balancing
Using Neural Network," in Springer, Computer
Science, 2006.
J. Zhu, Optimization of Power System Operation.
Hoboken, New Jersey: John Wiley & Sons, Inc., 2009.
C. B. Alexandre, A. Carlos, and Newton, "Main Chain
Representation for Evolutionary Algorithms Applied
to Distribution System Reconfiguration," IEEE Trans.
Power systems, vol. 20, Febrary, 2005.
A. Auguglio, L. Dusonchet, and M. Giuseppe, "Minimum
Losses Reconfiguration of MV distribution Networks
through Local Control of Tieswitches," IEEE Trans.
Power delivery, vol. 18, July, 2003.
M. E. Baran and F. F. Wu, "Network Reconfiguration in
Distribution Systems for Loss Reduction and Load
Balancing," IEEE Trans. Power delivery, vol. 7, 1989.
M. Siti, D. V. Nicolae, A. A. Jimoh, and A. Ukil,
"Reconfiguration and Load Balancing in LV and MV
Distribution Networks for Optimal Performance,"
IEEE Trans. Power delivery, vol. 22, pp. 2534-2540,
2007.
X. Yang, S. P. Carull, and K. Miu, "Reconfiguration,
Distribution, Automation and Control Laboratory:
Multiphase Radial Power Flow Experiment," IEEE
Trans. Power systems, vol. 20, August, 2005.
W. YU, HE, H. & ZHANG, N., "Optimal Reactive Power
Dispatch Using Particle Swarms Optimization
Algorithm Based Pareto Optimal Set," Berlin:
Springer-Verlag Berlin Heidelberg 2009, 2009.
A. Zaraki and M. F. Bin Othman, "Implementing Particle
Swarm Optimization to Solve Economic Load
Dispatch Problem," in Soft Computing and Pattern
Recognition, 2009. SOCPAR '09. International
NCTA 2011 - International Conference on Neural Computation Theory and Applications
222

Conference of, 2009, pp. 60-65.
B. P. Numbi, D. W. Juma, J. L. Munda, and A. A. Jimoh,
"Constraint Handling Approach in Optimal Reactive
Power Dispatch When Using Unconstrained Standard
Particle Swarm Optimization," in Proceedings of the
20th Southern African Universities Power Engineering
Conference, SAUPEC 2011, Cape town, 2011, pp. 7-
12.
A. H. Mantawy and M. S. Al-Ghamdi, "A new reactive
power optimization algorithm," in Power Tech
Conference Proceedings, 2003 IEEE Bologna, 2003,
p. 6 pp. Vol.4.
Eberhart and S. Yuhui, "Particle swarm optimization:
developments, applications and resources," in
Evolutionary Computation, 2001. Proceedings of the
2001 Congress on, 2001, pp. 81-86 vol. 1.
A NEW DISTRIBUTION SYSTEM RECONFIGURATION APPROACH USING PARTICLE SWARM
OPTIMIZATION AND NEURAL NETWORK
223
