USING CO-EXISTING ATTRACTORS OF A SENSORIMOTOR LOOP

FOR THE MOTION CONTROL OF A HUMANOID ROBOT

Matthias Kubisch, Benjamin Werner and Manfred Hild

Neurorobotics Research Laboratory, Department of Computer Science, Humboldt-Universität zu Berlin

Berlin, Germany

Keywords:

Humanoid robots, Limit cycle walking, Co-existing attractors, Neural controller, Sensorimotor loop.

Abstract:

The implementation of a biped robot gait is a challenging task within the ﬁeld of mobile robotics. Particularly,

when the robot is subject to unknown disturbance in constantly changing terrain, a stable and robust gait is

crucial. Regarding the machine together with the controller as an integrated system, the Dynamical Systems

Approach yields a new perspective on legged robots. So called Limit Cycle Walkers have shown their inherent

stability against moderate disturbances of different kinds because gaits can be constructed as attractors of the

dynamical system. Here, we will show how co-existing attractors in neural sensorimotor loops can be used for

the construction of robot gaits and for easy switching among behaviours. The results are demonstrated using

a humanoid robot with neural control and it is shown that walking and standing upright can be implemented

as co-existing attractors of the same pure sensorimotor loop.

1 INTRODUCTION

Legged robots should be able to walk around robustly

in different types of terrain. Also, it is desirable that

switching between various behaviours, like standing

upright, walking forward or walking in different di-

rections, takes place smoothly and reliably. Oscil-

lations have been discovered in countless biological

systems and almost all gaits comprise repetitive pat-

terns.

As (Hein, 2007; Hein et al., 2007) have shown,

different gaits for bipedal robots can be found by

artiﬁcial evolution using a central neural oscillator.

The robot’s actuators were driven using weighted and

phase-shifted variants of a single fundamental sine

wave but the resulting gaits were not inherently sta-

ble because they lacked sensory feedback.

Limit cycle walkers (Solomon et al., 2010;

Collins, 2005) have shown their beneﬁts in terms

of gait stability and simplifying the control strategy

when used in a tightly closed sensorimotor loop. So,

a gait has been successfully expressed as an attractor

of the overall system which underlines the potential

of the dynamical systems approach.

In the paper at hand we describe a sensorimotor

loop as the basis for humanoid robot walking and

show how to use the inherent properties of its attrac-

tors to switch the robot’s behaviours from standing to

walking and vice versa. The rest of the paper is or-

ganised as follows: In the next section, we brieﬂy re-

cap the terminology of discrete dynamical systems,

especially discrete time recurrent neural networks and

discuss switching between co-existing attractors. Sec-

tion 3 describes the implementation of a neural con-

troller for humanoid robot walking with the use of

the proposed co-existing attractors of the sensorimo-

tor loop. We demonstrate that behaviours like stand-

ing upright and walking can co-exist within the same

pure sensorimotor loop and that it is easy to switch be-

tween them. Finally, we give an outlook on our future

research.

2 NEURAL DYNAMICS

Dynamical systems theory (Guckenheimer and

Holmes, 1983; Thompson and Stewart, 1986) has be-

come an important tool for roboticists and turned out

to be beneﬁcial for the construction and understand-

ing of recurrent neural networks (Hild et al., 2007),

sensorimotor control loops (Martius et al., 2008) and

the physical system—the robot itself. To brieﬂy recap

the terminology, consider the neural network with the

update rule

x(t + 1) = tanh (Wx(t) + b + u(t)), (1)

385

Kubisch M., Werner B. and Hild M..

USING CO-EXISTING ATTRACTORS OF A SENSORIMOTOR LOOP FOR THE MOTION CONTROL OF A HUMANOID ROBOT.

DOI: 10.5220/0003682203850390

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 385-390

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

where x(t) ∈ M is the state of the dynamical system

at discrete time t ∈ N. The manifold M of all possi-

ble states is called the state space or phase space and

is M = (−1, +1)

⊂ R

for N neurons due to the hy-

perbolic tangent transfer function. A trajectory is an

ordered set of successive states, and is called a p-orbit

if it has a deﬁnite periodicity p. The weight matrix W

and bias vector b constitute the conﬁguration of the

system. Optionally, a control input u(t) is used to ex-

ternally manipulate the system.

A set towards which the system evolves over time

is called an attractor, which can be a point, curve

or manifold in phase space. Attractors can co-exist

within the same system and, depending on initial con-

ditions, the system evolves in either way. The set of

initial conditions leading to the same attractor is the

basin of that attractor, whereas borders between adja-

cent basins are called separatrices.

2.1 Co-existing Attractors in Discrete

Time Recurrent Neural Networks

Discrete time recurrent neural networks can exhibit a

variety of functionality—even if the number of neu-

rons is small. Consider the network’s conﬁguration

W =



1.282 −0.4

0.1 0.865



b =



0.04

0.02



(2)

with only two neurons and, for now, u(t) = 0. The

corresponding phase space is depicted in Figure 1.

This dynamical system has two co-existing attractors,

namely a stable ﬁxed point and a quasiperiodic orbit,

and in between the separatrix. The system’s outputs

are bounded by [−1, +1].

Usually we would expect an unstable ﬁxed point

inside the quasiperiodic orbit, a so-called repellor.

But in this conﬁguration we can identify another com-

plete basin inside and therefore we ﬁnd another, so-

Figure 1: Phase space of the neural network with co-

existing attractors. A basin with a stable ﬁxed point is being

enveloped by another basin with a quasiperiodic orbit.

Figure 2: Switching between co-existing attractors with

short and small control inputs, cf. also Figure 3.

called co-existing attractor. This attractor is a stable

ﬁxed point with the vector ﬁeld having a curl in that

point. The expected unstable regime has become a

separatrix, here in form of a closed unstable orbit.

Please note, if we would invert the system by in-

terchanging inputs and outputs, the time is ﬂowing

backwards and attractors become unstable. In turn,

formerly unstable areas become attractors. So, the

separatrix becomes a stable orbit and the area out-

side the former quasiperiodic orbit diverges beyond

all bounds. This is due to the poles of the inverse hy-

perbolic tangent.

2.2 Switching Co-existing Attractors

Switching between co-existing attractors can be re-

alised by introducing a controller u(t) = K(x(t))

which usually depends on the current state and pro-

vides the control input u(t). Switching from the stable

ﬁxed point to the quasiperiodic orbit takes place when

the control input is powerful enough to hop over the

separatrix as depicted in Figure 2.

Here, the direction of the control input is of lower

importance since the orbit envelops the ﬁxed point.

Switching to the basin of the ﬁxed point mainly de-

pends on the phase of the oscillation. So the controller

needs an exact timing and pulse shape for a suitable

jump.

Actually, the system together with the controller

form a new dynamical system of higher dimension

than the initial one. But, since we are considering

short and small control inputs, we omit additional di-

mensions for convenience.

Switching between attractors is of major interest

since different behaviours can be expressed as co-

existing attractors (Hild and Kubisch, 2011). In other

NCTA 2011 - International Conference on Neural Computation Theory and Applications

386

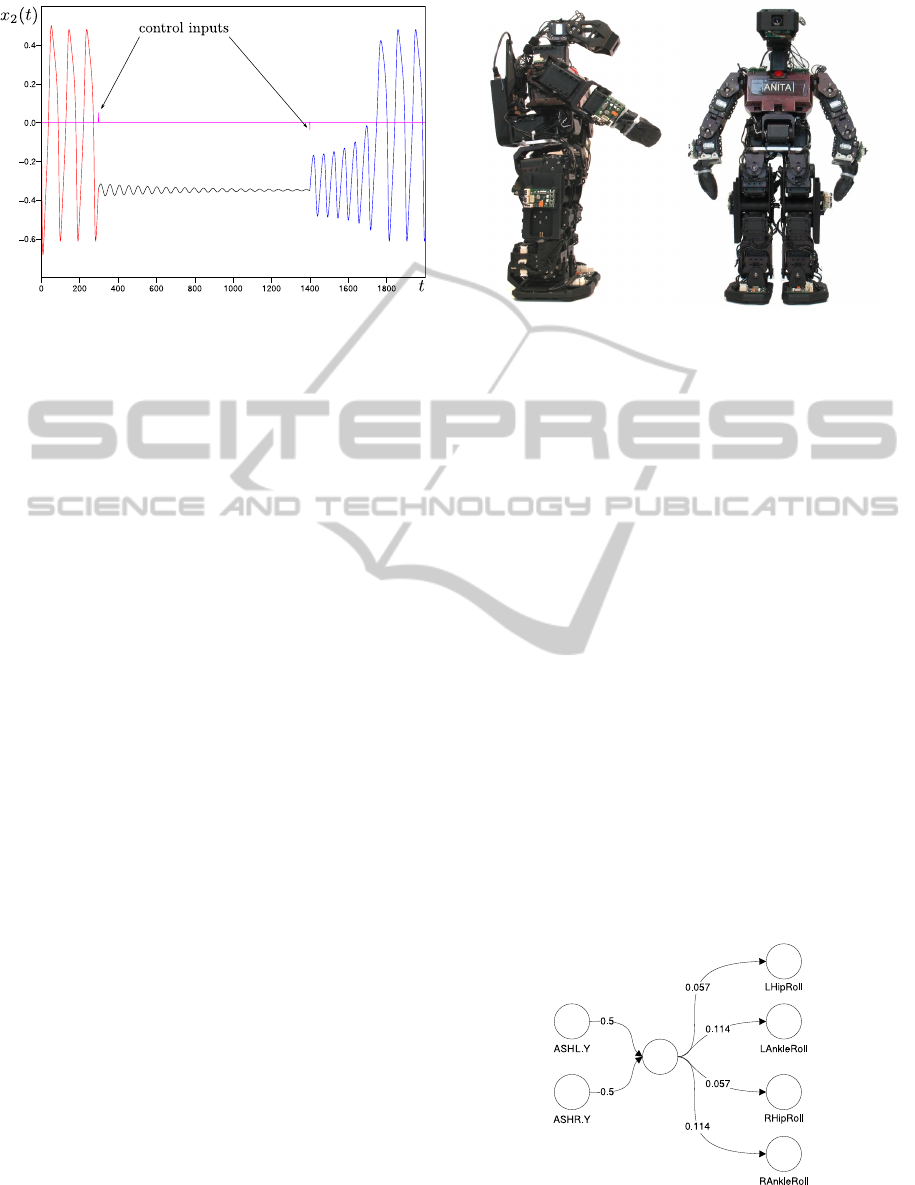
Figure 3: Switching between co-existing attractors: output

of x

. Small control inputs u(t

) = (0, 0.05) and u(t

) =

(0, −0.04) are exerted to the system, each with a length of

only one time step.

words, to blend over from one behaviour to another,

we simply have to switch attractors. The next sec-

tion describes how behaviours like walking and stand-

ing upright can be formulated as attractors of the

robot’s sensorimotor system and how switching be-

tween them both can take place.

3 A PURE SENSORIMOTOR GAIT

The type of gait that is to be shaped, highly depends

on the robot’s morphology, i. e. actuators, elasticities,

sensors and so on. For a better understanding of the

complex interplay, one has to bring to mind which

parts are mandatory to shape an attractor. A generic

walking pattern can therefore be separated into parts

resulting in the following sequence:

First, the weight has to be shifted within the

frontal plane to one side using the hip and ankle roll

motors. This lifts the hip and enables sagittal leg mo-

tion. The ankle and hip pitch motors of the stance

leg can now push the body forward so that the swing

leg has enough distance to the ground and can freely

move forward. After the swing leg has touched the

ground steadily, the weight is shifted back to the other

side. The necessary weight shift is achieved by an os-

cillatory lateral movement of the full body. Walking

forward can then be realised by superposing sagittal

leg movements with the same frequency using left and

right, hip and ankle roll motors.

3.1 Structure of the Sensorimotor Loop

An upright standing humanoid robot can approxi-

mately be regarded as an inverted pendulum with a

Figure 4: The A-Series humanoid robot used for walking

experiments. Among others, two acceleration sensors are

mounted on top of the robot’s shoulders.

single contact point to the ground. To stabilise the up-

right posture the controller has to exert enough torque

to swing back the robot in case of disturbance. To

initiate the walking motion, the controller has to shift

the weight smoothly. This is realised by direct sen-

sory feedback forming a closed sensorimotor loop.

The A-Series humanoid robot (Hild, 2007;

Werner, 2008) as depicted in Figure 4 possesses six-

teen 2D acceleration sensors which are distributed all

over the body. Two of them are mounted on top of the

robot’s shoulders and their sensory values are added

together to measure the lateral and sagittal accelera-

tion of the robot’s torso. The lateral sensory informa-

tion is weighted and fed back to the left and right, hip

and ankle roll motors (cf. Figure 5).

Robot and neural control together constitute a dy-

namical system holding co-existing attractors such as

lying on back or belly. Even when the motors are

not actively driven, due to stiction and activated mo-

tor brakes, standing upright is also an attractor, how-

ever with a very small basin. Imprecisely speaking,

this is a blurred ﬁxed point, i. e. a densely packed

Figure 5: First attempt of a sensorimotor loop for robot

walking. Lateral acceleration data are directly fed back to

the actuators.

USING CO-EXISTING ATTRACTORS OF A SENSORIMOTOR LOOP FOR THE MOTION CONTROL OF A

HUMANOID ROBOT

387

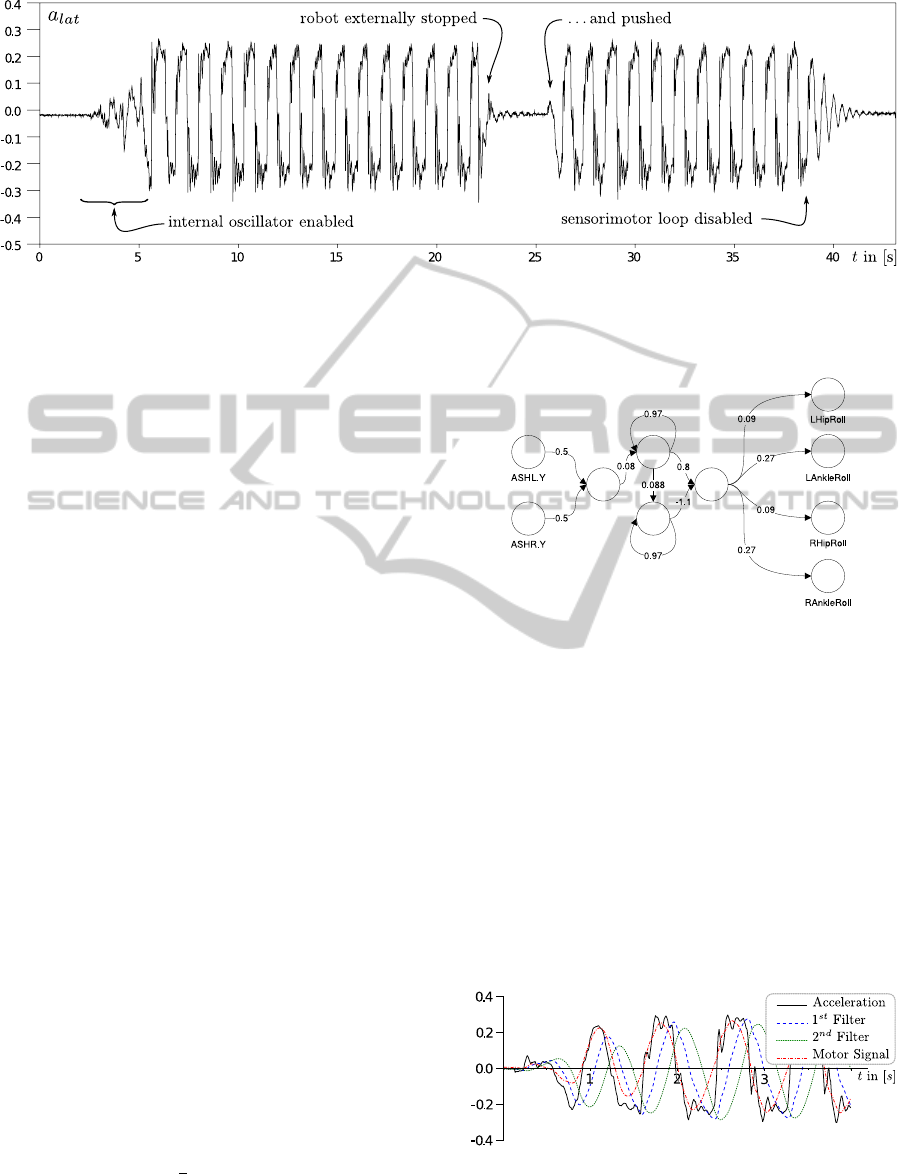
Figure 6: Lateral acceleration data of an about 40 second trial. At the beginning, the internal oscillator initiates the lateral

body movement. After approximately 22 seconds the motion is manually stopped and again reinitialised by the experimenter.

Finally, the controller internally disables the sensorimotor loop causing the robot to stop.

set of ﬁxed points. So, the stated postures are all sta-

ble ﬁxed points of the system. When driving a lat-

eral oscillation the dynamical system now possesses

a quasiperiodic orbit or limit cycle. A small impulse

within the frontal plane, e. g. a gentle push, makes the

robot leave the ﬁxed point standing and start swing-

ing. In turn, if the robot is being externally held by

the experimenter, the system falls back into the basin

of the standing posture’s ﬁxed point. Figure 6 depicts

the data from lateral acceleration sensors during a 40

second trial with several starts and stops of the os-

cillation. Figure 9 on the next page shows successive

snapshots of an A-Series humanoid robot, performing

lateral oscillation.

3.2 Widening the Basin of Attraction

For now, the simplicity of our ﬁrst attempt to build

this sensorimotor loop has a drawback: The outputs

of the acceleration sensors usually contain a variety

of different high frequencies due to non-linearities in

the motion of the physical system and sensor noise.

Most essentially, when the feet are touching or are

lifted from the ground, these events produce percep-

tible impulses yielding salient peaks in the acceler-

ation data. If such high frequency components are

fed back to the motors, this would lead to unintended

power consumption and heat production as well as ad-

ditional non-linear distortion of the system’s lateral

movement. Also, the correct phase is needed for a

quick buildup of the oscillation. Therefore, the loop

is extended by a neural implementation of two ﬁrst

order recursive ﬁlters (cf. Figure 7).

The acceleration signal will be low-pass ﬁltered

and phase shifted by

per neuron. Approximately,

the ﬁltering neurons’ outputs can be regarded sinu-

soids with almost the same amplitude and fundamen-

tal. Thus, mixing those signals yields another one

Figure 7: Sensorimotor loop with low-pass ﬁltering and

phase correction. Filtering is implemented as neural ana-

logues of recursive ﬁlters.

with the same frequency but with different ampli-

tude and phase. The mix is then fed to the motors.

Figure 8 shows the acceleration signal and its low-

pass ﬁltered variants, together with the mixed and

again phase-corrected motor signal. As can be seen,

ﬁltering performed effectively, resulting in a strong

reduction of high frequency components and a cor-

rected phase. Moreover, it turned out that damping

the high frequencies widens the basin of attraction for

the quasiperiodic orbit and therefore increases the ro-

bustness of the robot’s gait.

Figure 8: Acceleration data and its low-pass ﬁltered vari-

ants; mixed and phase-corrected motor signal.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

388

Figure 9: An A-Series humanoid robot performing lateral oscillation.

3.3 Stability of the Walking Pattern

Amplitude and frequency of the gait usually change

on different terrain; especially on soft surfaces, e. g.

on carpet, the amplitude of the oscillation is strongly

decreased. Keeping synaptic weights constant, it can

be mentioned that robots of the same series slightly

differ in walking amplitude and frequency. This is

due to minor variations in construction, material and

battery charge level as well as mechanical wearout of

gears and soles.

Due to its attractor properties, the gait has an in-

herent stability against small disturbances, e. g. mi-

nor variations in surface structure. For larger distur-

bances or major environmental variations like chang-

ing ground slopes or obstacles, further balancing

methods are required.

For now, knee joints have not yet been used, yield-

ing a penguin-like gait. Bending knees, the ampli-

tude of the lateral oscillation can be decreased since

the legs need less distance to the ground. This will

very likely improve the gait stability once again and

reduces the risk to fall over sidewards.

3.4 Starting and Stopping the Motion

At the beginning, the robot is initialised at the stable

ﬁxed point, i. e. the upright posture. So far, the robot

needs an external impulse, e. g. a gentle push from

the experimenter, to get out of the basin of the ﬁxed

point, into the basin of the quasiperiodic attractor, and

hence, starts the lateral oscillation.

When the robot is to act autonomously the neural

controller has to initialise the swinging motion on its

own to leave the stable ﬁxed point on a transition to

the quasiperiodic orbit. For this, an internal oscillator

with almost the same eigenfrequency as the robot’s

sensorimotor oscillation is temporarily connected to

the actuators to initiate the motion smoothly and ro-

bustly.

The oscillator is likewise implemented as a neu-

ral network (Pasemann et al., 2003) and well dosed

through neural gates. When the amplitude has

reached a certain threshold, the oscillator is cut off

from the sensorimotor loop. On the other hand, if the

controller has to stop the motion from inside, the sen-

sory feedback is simply cut off with the use of a neu-

ral gate. After this, the oscillation fades out, cf. once

again Figure 6.

This means that the lateral oscillation and thus the

walking pattern can be started and stopped either from

outside the body by an external disturbance or from

inside by the controller itself. This equivalence may

shed new light on how behaviours of living beings are

triggered and merged.

4 CONCLUSIONS AND

OUTLOOK

Using the dynamical systems approach, we have

shown that behaviours like walking and standing can

co-exist as attractors of the same pure sensorimotor

loop. For this, we used a neural implementation of a

minimalist control loop where acceleration data are

directly fed back to the actuators. We further ex-

tended the controller with a ﬁltering mechanism that

widens the basin of attraction for the walking pattern

and thus enhance the stability of the gait. We state

that attractor-based behaviours are inherently robust

and can easily be switched while producing smooth

transitions among behaviours.

Since no explicit body model is required, the pro-

posed technique is independent of the humanoid robot

platform used for walking experiments. We have suc-

cessfully tested our approach with the humanoid robot

Myon (Hild et al., 2011). Although the Myon robot

signiﬁcantly differs in size, weight and the type of

actuation, we were able to gain comparable results

which will be reported in an upcoming paper. If accel-

eration sensors are not available, the position sensors

of the hip roll joints can be used alternatively.

The proposed sensorimotor loop can be enhanced

in terms of reactivity and stability by replacing the

aforementioned ﬁltering neurons with a Slow Feature

Analysis (Höfer and Hild, 2010). This also extends

the robot’s capabilities with a fall-over prediction by

detecting slow varying changes in sensory data.

Also the shape and elastic properties of legs and

feet can increase the stability and efﬁciency of the

gait (Collins, 2005; Schneider, 2006). Arched foot

shapes apparently outperform pure ﬂat and rectan-

USING CO-EXISTING ATTRACTORS OF A SENSORIMOTOR LOOP FOR THE MOTION CONTROL OF A

HUMANOID ROBOT

389

gular shapes in terms of dynamics and controllabil-

ity. Current work incorporates the redesign of a hu-

manoid robot’s foot under these pure mechanical as-

pects (Richter, 2011). Furthermore, we currently en-

hance the sensorimotor gait with recent balance re-

covery techniques using the humanoid robot Myon

(Kubisch et al., 2011).

ACKNOWLEDGEMENTS

The authors would like to thank all the former mem-

bers of the Humanoid Team Humboldt for their great

work to bring the ﬁve A-Series robots to life. This

work has been partially supported by the European

research project ALEAR (FP7, ICT-214856).

REFERENCES

Collins, S. H. (2005). A Bipedal Walking Robot with Efﬁ-

cient and Human-Like Gait. In Proceedings of IEEE

International Conference on Robotics and Automa-

tion, pages 1995–2000.

Guckenheimer, J. and Holmes, P. (1983). Nonlinear Oscil-

lations, Dynamical Systems and Bifurcations of Vector

Fields. Springer-Verlag, New York.

Hein, D. (2007). Simloid: Evolution of Biped Walking

Using Physical Simulation. Master’s thesis, Depart-

ment of Computer Science, Humboldt-Universität zu

Berlin.

Hein, D., Hild, M., and Berger, R. (2007). Evolution of

biped walking using neural oscillators and physical

simulation. In RoboCup 2007: Proceedings of the In-

ternational Symposium LNAI, Springer.

Höfer, S. and Hild, M. (2010). Using Slow Feature Analysis

to Improve the Reactivity of a Humanoid Robot’s Sen-

sorimotor Gait Pattern. In Proceedings of the Interna-

tional Conference on Neural Computation (ICNC).

Hild, M. (2007). Neurodynamische Module zur Bewegungs-

teuerung autonomer mobiler Roboter. PhD thesis, De-

partment of Computer Science, Humboldt-Universität

zu Berlin.

Hild, M. and Kubisch, M. (2011). Self-Exploration of

Autonomous Robots Using Attractor-Based Behav-

ior Control and ABC-Learning. In Proceedings of

the 11th Scandinavian Conference on Artiﬁcial Intel-

ligence, Trondheim, Norway.

Hild, M., Kubisch, M., and Göhring, D. (2007). How to

Get from Interpolated Keyframes to Neural Attractor

Landscapes – and Why. In Proceedings of the 3rd Eu-

ropean Conference on Mobile Robots, Freiburg, Ger-

many.

Hild, M., Siedel, T., Benckendorff, C., Kubisch, M., and

Thiele, C. (2011). Myon: Concepts and Design of a

Modular Humanoid Robot Which Can Be Reassem-

bled During Runtime. In Proceedings of the 14th

International Conference on Climbing and Walking

Robots, Paris, France.

Kubisch, M., Benckendorff, C., and Hild, M. (2011). Bal-

ance recovery of a humanoid robot using cognitive

sensorimotor loops (CSLs). In Proceedings of the

14th International Conference on Climbing and Walk-

ing Robots and the Support Technologies for Mobile

Machines.

Martius, G., Fiedler, K., and Herrmann, J. M. (2008). Struc-

ture from Behavior in Autonomous Agents. In Pro-

ceedings of the IEEE/RSJ International Conference on

Intelligent Robots and Systems, pages 858–862.

Pasemann, F., Hild, M., and Zahedi, K. (2003). SO(2)-

Networks as Neural Oscillators. In Proceedings of the

International Work Conference on Artiﬁcial and Nat-

ural Neural Networks (IWANN), pages 144–151.

Richter, E. (2011). Redesign und Fertigung eines Fußes

für humanoide Roboter. Master’s thesis, Leibniz In-

stitute of Polymer Research, Technische-Universität

Dresden.

Schneider, A. (2006). Local Positive Velocity Feedback

for the Movement Control of Elastic Joints in Closed

Kinematic Chains: A Modelling and Simulation Study

of a 2DoF Arm and a 3DoF Insect Leg. PhD thesis,

Department of Biology, Universität Bielefeld.

Solomon, J. H., Wisse, M., and Hartmann, M. J. (2010).

Fully Interconnected, Linear Control for Limit Cycle

Walking. Adaptive Behavior, 18.

Thompson, J. M. T. and Stewart, H. B. (1986). Nonlinear

Dynamics and Chaos. Wiley, Chichester U.K.

Werner, B. (2008). Sensomotorische Erzeugung eines

Gangmusters für humanoide Roboter. Studienarbeit

am Lehrstuhl für Künstliche Intelligenz, Humboldt-

Universität zu Berlin.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

390