PARALLEL EVALUATION OF HOPFIELD NEURAL NETWORKS

Antoine Eiche, Daniel Chillet, Sebastien Pillement and Olivier Sentieys

University of Rennes I, IRISA, INRIA, 6 Rue de Kerampont, Lannion, France

Keywords:

Hopﬁeld neural networks, Parallelization, Stability, Optimization problems.

Abstract:

Among the large number of possible optimization algorithms, Hopﬁeld Neural Networks (HNN) propose in-

teresting characteristics for an in-line use. Indeed, this particular optimization algorithm can produce solutions

in brief delay. These solutions are produced by the HNN convergence which was originally deﬁned for a se-

quential evaluation of neurons. While this sequential evaluation leads to long convergence time, we assume

that this convergence can be accelerated through the parallel evaluation of neurons. However, the original

constraints do not any longer ensure the convergence of the HNN evaluated in parallel. This article aims to

show how the neurons can be evaluated in parallel in order to accelerate a hardware or multiprocessor imple-

mentation and to ensure the convergence. The parallelization method is illustrated on a simple task scheduling

problem where we obtain an important acceleration related to the number of tasks. For instance, with a number

of tasks equals to 20 the speedup factor is about 25.

1 INTRODUCTION

Hopﬁeld Neural Network (HNN) is a kind of recur-

rent neural network that has been deﬁned for associa-

tive memory or to solve optimization problems (Hop-

ﬁeld and Tank, 1985). They have been used to solve

a lot of optimization problems such as travelling sale-

man (Smith, 1999), N-queens (Ma

ndziuk, 2002) or

task scheduling (Wang et al., 2008). Our context is

to solve the task scheduling problem at runtime, and,

therefore, the execution time of the algorithm is cru-

cial. HNN allows for an efﬁcient hardware implemen-

tation because the control logic to evaluate a HNN

is really simple. A HNN provides a solution when

the network has converged, and this convergence has

been demonstrated under some constraints on the in-

put and connection weights, and with a sequential

evaluation of neurons. This article focuses on a paral-

lel evaluation model of HNNs in order to further im-

prove the execution time.

A lot of authors proposed different approaches to

improve the quality of generated solutions, but the lit-

erature about improvements of execution time is not

very large. Moreover, in this kind of works, the HNN

convergence constraints are not often respected, then

a controller is needed to stop the network when the

solution seems to be satisfactory. In this article, we

focus on reducing the HNN convergence time by eval-

uating several neurons simultaneously. Because this

evaluation method modiﬁes the initial HNN conver-

gence constraints, we recall the convergence proof in

order to exhibit the required properties ensuring the

convergence. Then, we show how to build a HNN

which can be evaluated in parallel while ensuring con-

vergence.

We present a parallelization method of HNN eval-

uation which aims to

• decrease the evaluation time of the HNN, and

• ensure the convergence.

Section 2 is a brief presentation of the HNN

model. Section 3 presents some related works about

the improvement of HNN evaluation. Since sev-

eral neurons are evaluated simultaneously, we recall

the convergence proof at the beginning of Section 4.

Then, we show how the evaluation must be achieved

to ensure the convergence. In Section 5, we present

improvements brought by our parallelization method

on a simpliﬁed scheduling problem. Finally, Section

6 concludes and gives some perspectives.

2 HOPFIELD NEURAL

NETWORK

In this work, HNNs are used to solve optimization

problems. This kind of neural networks is modeled as

a complete directed graph. Figure 1 presents a HNN

with three neurons. Each neuron has a threshold (in-

248

Eiche A., Chillet D., Pillement S. and Sentieys O..

PARALLEL EVALUATION OF HOPFIELD NEURAL NETWORKS.

DOI: 10.5220/0003682902480253

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 248-253

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

put) value (I

for neuron X

) and receives connections

i, j

from all other neurons (e.g. W

1,2

and W

1,3

for

). In order to simplify notation and implementa-

tion, when the weight of a connection between two

neurons is equal to zero, these neurons are not con-

nected by an edge.

2,1

3,1

1,2

3,2

1,3

2,3

Figure 1: Example of Hopﬁeld neural network with three

neurons.

A neuron has a binary state, which is either ac-

tive or inactive, respectively represented by values 1

and 0. A HNN can be evaluated in several ways, the

most common is called sequential mode: neurons are

randomly evaluated one by one. In this case, the eval-

uation of a neuron is given by

= H(

∑

j=1

×W

i j

+ I

), (1)

where H(x) =



0 if x ≤ 0

1 if x > 0

, (2)

and n the number of neurons in the network, X

the

state of the neuron i, W

i j

the connection weight from

neuron j to neuron i, I

the threshold of neuron i. We

then deﬁne respectively the state and threshold vector

of the network X = [X

] and I = [I

] of size n and the

n × n connection matrix W = [W

i j

The main idea behind using HNN for solving op-

timization problems is to map the optimization prob-

lem to a particular function called the energy func-

tion. From this energy function, the parameters (input

and connection weights) of the network can be de-

rived. The dynamics of the network is launched until

it reaches a stable state. When the network becomes

stable, the state of the neurons represents one possible

solution.

3 RELATED WORKS

To parallelize the evaluation of a HNN, two main

techniques can be used. The ﬁrst one is based on

the parallelization of the internal neuron computation,

while the second one is to update several neurons at

the same time.

In (Del Balio et al., 1992), the authors proposed an

optimized evaluation of HNN. To make the evaluation

of the network faster, they parallelize the state update

of a neuron. Eq. (1) exhibits some multiplications and

an accumulation during the update process of a neu-

ron. The authors parallelize all multiplications and

use a special communication infrastructure to accel-

erate the accumulation. When the number of neu-

rons is sufﬁciently large, the theoretical speedup fac-

tor is similar to the number of neurons. In (Domeika

and Page, 1996), the authors propose some techniques

which are speciﬁc for HNNs. They have observed

that neurons almost share the same evaluation expres-

sion. They compute a common expression for sev-

eral neurons, then a small expression is subtracted to

the global expression for each neurons. This tech-

nique factorizes evaluations of several neurons. While

these methods improve the evaluation time of a HNN,

they do not modify the convergence properties of a

HNN. Although we propose another way to improve

the convergence time, these methods can also be used

together with our method.

In (Domeika and Page, 1996), several neurons are

evaluated in parallel, on different processing units.

Because, in general HNN implementations include

more neurons than processing units, several sets of

neurons are created. All neurons of a set are sequen-

tially executed on the same processor. Then, the pro-

posed method to create these sets try to group some

similar neurons in order to share some parameters,

such as the value of weights. But, the network conver-

gence problem is not taken into account in this work.

(Ma

ndziuk, 2002) presents an important review

of HNN used to solve the N-queens problem. For

this problem, it has been shown that the initial Hop-

ﬁeld constraint on the self-feedback connection sig-

niﬁcantly decreases the quality of results. Some neg-

ative self-feedback connections are used, the conver-

gence of the HNN is no longer guaranteed.

Finally, we can also note that authors of (Wilson,

2009) proposed a HNN which is able to represent the

behavior of several HNNs. Because they do not im-

prove the convergence time of a HNN, this work is

out of the scope of this article.

4 PARALLEL NEURAL

NETWORK EVALUATION

In this section, we ﬁrst present a convergence proof

of the HNN parallel evaluation. This proof shows

that if the connection weight between two neurons is

positive (i.e. greater than or equal to 0), these neu-

rons can be evaluated in parallel without affecting the

convergence property. The second part of this section

presents a way to build a HNN that respects rules to

ensure convergence.

PARALLEL EVALUATION OF HOPFIELD NEURAL NETWORKS

249

4.1 Convergence of the HNN

A HNN is deﬁned to ensure convergence towards one

solution of the problem. The convergence property

means that the network evolves to a stable state where

the energy function has reached a local minima. To

ensure this convergence, the neural network must re-

spect some constraints that are deﬁned in the initial

Hopﬁeld article (Hopﬁeld and Tank, 1985) for the se-

quential mode: the connection matrix must be symet-

ric and its diagonal elements must be positive.

Convergence constraints appear from the proof of

the network convergence and the proof is strongly

bound to the chosen evaluation mode. In this section,

we develop from (Kamp and Hasler, 1990) a conver-

gence proof of a HNN using a parallel evaluation.

To be able to evaluate neurons in parallel, the state

vector X is partitioned into K blocks of arbitrary size

such as



,...,X



, (3)

where X

is the transposed vector of X representing

neuron states. Then, the connection matrix W and the

input vector I are partitioned in the same way.

W =







... W







I =













(4)

Neurons belonging to the same block X

are eval-

uated in parallel and all the blocks are evaluated se-

quentially. The evaluation order of these blocks does

not affect the convergence and could be random. To

simplify notations, we consider a sequential evalua-

tion order of all blocks X

from 1 to K. From Eq. (1),

the neuron update of the block X

becomes

(t + 1) = H

k−1

∑

i=1

(t + 1) × W

(5)

∑

i=k

(t) × W

− I

where X

(t) denotes the evaluation of X

at iteration t.

To evaluate the block X

(t + 1), the value at iteration

t + 1 of blocks X

,...,X

k−1

and the value at iteration

t of blocks X

,...,X

are used.

To use this parallel evaluation mode, the network

convergence must be veriﬁed with a parallel evalua-

tion of neurons. In (Kamp and Hasler, 1990), a theo-

rem about the convergence with a parallel evaluation

is proposed. By using a parallel dynamics, the HNN

converges to a ﬁxed point if the matrix W is symmet-

ric and if diagonal blocks W

are positive or equal to

zero.

To prove this convergence, the Lyapunov theo-

rem is used and we show that the energy function

is strictly decreasing during the network evolution.

Hopﬁeld proposed to use the following energy func-

tion to prove the network convergence

E(X) = −1/2

∑

i j

× X

−

∑

× I

. (6)

To verify if the energy function is decreasing, the

sign of the difference between two successive itera-

tions is evaluated. Without loss of generality, we con-

sider that the ﬁrst block of X is evaluated. To simplify

notations, we rewrite the state vector X, the connec-

tion matrix W and the input vector I as

X =





,W =



V W



,I =





. (7)

It is important to note that the matrix W is supposed

symetric to achieve the proof. Moreover, it is not a

strong limitation because connection values are natu-

rally symetric when a HNN is built to solve a problem.

This constraint is studied and relaxed in (Xu et al.,

1996).

From Eqs. (3), (7) and (6), we can express the

difference between two successive iterations as:

∆(E(X)) = E(X(t + 1)) − E(X (t)) =

−

z }| {

(t + 1) − X

(t)]

z }| {

(t) + V

(t) + I

]

−

z }| {

(t + 1) − X

(t)]W

z }| {

(t + 1) − X

(t)].

(8)

∆(E(X)) has to be negative to prove the conver-

gence of the HNN evaluation using K parallel blocks.

If X

(t + 1) = X

(t), then a ﬁxed point is reached

and the HNN did not evolve. In the following, we

consider that X

(t + 1) 6= X

(t). In this case, because

elements of X

belong to {0, 1}, X

(t +1)−X

(t) can

be equal to −1 or 1.

If products A

× A

and B

× W

× B

are both

positives, ∆(E(X)) is negative and therefore the func-

tion E(X) is proved decreasing. In the following the

sign of these two products is studied.

Concerning the product A

× A

of Eq. (8), from

Eq. (5), we have

(t + 1) = H(W

(t) +V

(t) + I

) = H(A

(9)

Then, from Eq. (2), if an element i of X

(t + 1) is

equal to 0, the element i of A

is then negative. Be-

cause we consider that X

(t + 1) 6= X

(t), when an

NCTA 2011 - International Conference on Neural Computation Theory and Applications

250

element i of X

(t + 1) is equal to 0, the element i of

(t) is equal to 1, and the element i of A

is then

negative (equal to −1). In this case, A

and A

are

both negatives and their product is positive.

We have shown that when an element i of X

(t +

1) is equal to 0, the product A

× A

is positive. An

analogical reasoning can be applied to an element i

of X

(t + 1) that is equals to 1. Therefore, we can

conclude that elements of A

×A

are always positive.

Concerning the product B

×W

×B

of Eq. (8),

the sign of an element depends on the sign of W

. If

all elements of W

are positive then B

× W

× B

is positive.

Finally, because A

× A

and B

× W

× B

are

always positive, the sign of ∆(E(X )) is negative and

hence the energy function Eq. (6) is strictly decreas-

ing until a ﬁxed point is reached. By the Lyapunov

theorem, we can conclude that the network reaches a

ﬁxed point if

• the matrix W is symmetric, and

• the diagonal blocks W

are positive.

This theorem is a sufﬁcient but not necessary con-

dition to ensure convergence. We are working on a

more indepth study of the energy function in order to

exhibit less restrictive constraints.

4.2 Application to Optimization

Problem

Since the needed constraints are known, it is now pos-

sible to explain how a HNN can be evaluated in paral-

lel for an optimization problem. To evaluate the HNN

in parallel, we have to build some packets of inde-

pendent neurons. Neurons belonging to a packet are

evaluated simultaneous.

We can note that in our HNN applications, we

never use strictly positive connections. Thus, we con-

sider that we can build a packet of parallel neuron if

connections between these neurons are equal to zero.

Figure 2 shows a connection matrix example of a

HNN containing six neurons. This connection matrix

contains three diagonal blocks with elements equal to

zero. Then, neurons of this network can be grouped

into three parallel packets: {1,2}, {3} and {4,5,6}.

From Section 4.1, the diagonal block of the matrix

must be positive to ensure that the network reaches a

stable state. Thus, if the connection values in the di-

agonal block are equal to zero, this constraint is satis-

ﬁed.

To construct packets of neurons which could be

evaluated in parallel, we have to ﬁnd neurons that are

not connected. The next section presents the construc-

tion of packets on a example.

1 2

5 6

i j

Figure 2: Example of a connection matrix for a HNN evalu-

ated in parallel. Diagonal matrix elements are equal to zero.

All other elements W

i j

are negative or equal to zero.

5 APPLICATION TO A

SCHEDULING PROBLEM

To illustrate the parallel evaluation of a HNN, the

single machine scheduling problem (Sidney, 1977) is

treated. It consists in determining for each scheduler

“tick” which task has to be executed. Then, the HNN

aims at ﬁnding a valid task scheduling scenario on

a period which corresponds to the sum of execution

time of all tasks.

Figure 3 presents an example of the neural model

of the scheduling problem. In this example, the

scheduling period p is equal to six scheduler “ticks”,

and there are four tasks. The neural network con-

tains 6 ×4 neurons, one neuron for each task and each

“tick”. An activated neuron means the associated task

will be executed at the corresponding “tick”.

To deﬁne connections and input values of the

HNN, some k-outof-n rules deﬁned in (Tagliarini

et al., 1991) are used. A k-outof-n rule ensures that

k neurons are active among n when a stable state is

reached.

All used k-outof-n rules are represented by dotted

rectangles in Figure 3. All neurons belonging to a

rectangle form a complete digraph. For each task, a

k-outof-n rule is applied with n equals to the number

of cycles needed to execute the task on the processor,

and k is set to the required execution ticks for each

task. Moreover for each tick, just one task can be

executed, then a 1-outof-n is applied on each column

with n set to the number of tasks.

To build packets of neurons, disconnected neurons

have to be selected. On Figure 3, we can note that

there is no connection between diagonal neurons. For

example, neurons (3,0), (2,1), (1,2) and (0,3) are

disconnected, so they can form a packet. Thus, it is

PARALLEL EVALUATION OF HOPFIELD NEURAL NETWORKS

251

1 2

Cycle

(3,0)

(2,1)

(1,2)

(0,3)

Figure 3: Graphical representation of all applied k-outof-n

rules.

possible to group these neurons into a parallel packet.

6 EXPERIMENTATIONS

In this section, a comparison is presented between the

sequential evaluation and the parallel evaluation of the

HNN to exhibit the improvement factor provided by

our parallelization method. The considered applica-

tion is the scheduling problem presented in Section

The ﬁrst step is to build packets of neurons for the

parallel evaluation of the network. Figure 4 presents

the size of packets compared with the number of neu-

rons. In our study example, the size of a packet is

the number of tasks. To build a task set of size t, t

tasks are generated with a random task duration be-

longing to [1,5]. The scheduling period is the sum of

task durations in order to have enough time to sched-

ule all tasks. Thus, the number of neurons belongs to

,5 ×t

]. Figure 4 describes the data set used in the

rest of this study.

The metric used for this comparison is the number

of packet evaluations. When the sequential evaluation

is used, a packet consists of one neuron. Then, to

compare these two modes, we consider that we are

able to evaluate a packet as fast as a neuron. In this

case, the execution time of a HNN is strictly bound to

the number of packet evaluations in both modes.

Figure 5 presents the results of several neural net-

work evaluations. These evaluations are achieved

with a HNN software simulator developped in our

team. For each network, a sequential and a parallel

evaluation achieved to show the gain obtained by our

parallelization method. In both modes, packets are

evaluated in a random order. Simulations stop when a

stable state is reached without the need of a external

controller. Then, the number of evaluations contains

the last iteration which is needed to exhibit the stable

200

400

600

800

1000

1200

1400

1600

1800

2000

Number of neurons

Tasks number / packets size

Figure 4: Size of packets compared with number of neu-

rons. Because the size of packet is equal to the number of

task, the abscissa represents the task number or the packet

size.

state.

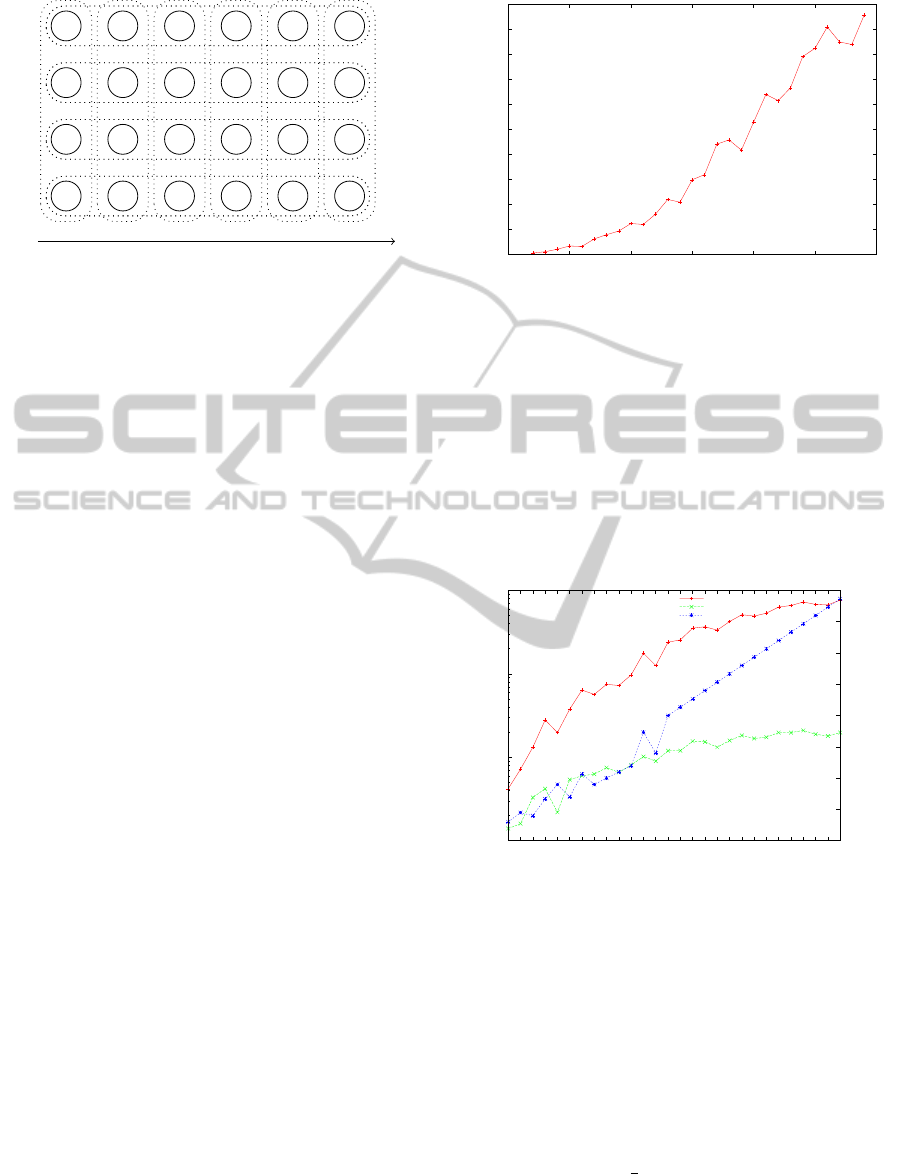
Figure 5 shows that the improvement is really high

and moreover increases with the number of neurons

because the size of packets depends on the number of

neurons. As a example, for about 2000 neurons, the

parallized version is 38 times faster than the sequen-

tial version.

100

1000

10000

126

160

189

250

242

324

442

420

600

640

884

918

836

1060

1281

1232

1334

1584

1650

1820

1701

1680

1914

Number of packet evaluations

Speed up factor

Number of neurons

Number of sequential evaluations

Number of parallel evaluations

Speed up

Figure 5: Number of packets evaluations for a sequential

and a parallel evaluation.

The speedup factor presented in Figure 5 supposes

that architecture executing the HNN has enough re-

sources to evaluate in parallel all neurons present in a

packet. Otherwise, it is necessary to split all packets

into several sub-packets which increases the execu-

tion time.

From Section 5, the number of neurons in a paral-

lel packet is equal to the number of tasks t. Consider-

ing n as the number of neurons in a HNN, the number

of packets is equal to

. The number of packets in the

sequential mode is t times higher than the number of

packets in the parallel mode. Therefore, the speedup

should be approximately equal to the task number t.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

252

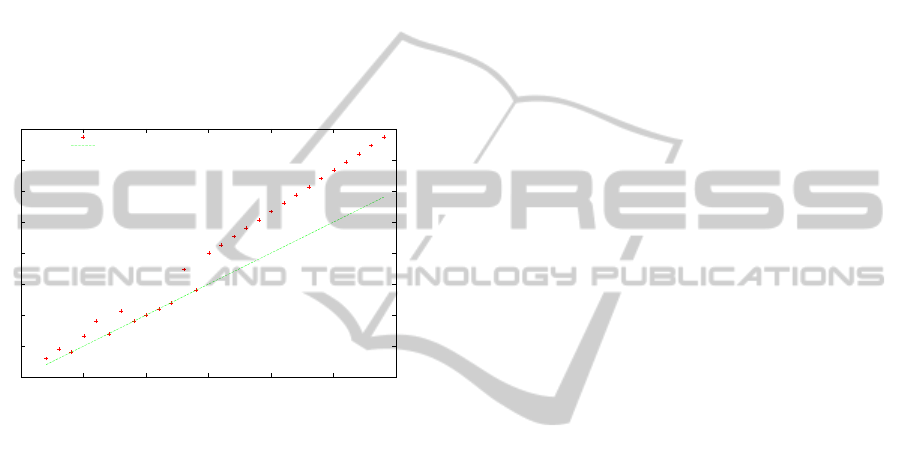
Figure 6 presents the speedup factor compared

to the number of tasks. We can observe that the

speedup factor is equal or higher than t. To reach the

stable state, all neurons are evaluated several times.

One evaluation of all neurons is called an iteration.

The speedup factor could be higher than the number

of tasks because the parallelization can decrease the

number of iterations. This is mainly due to an ap-

propriated neurons evaluation order. In the sequen-

tial mode, we can agree the diagonal evaluation or-

der is the fastest order to reach a stable state: at two

consecutive times, neurons corresponding to different

tasks and ticks are evaluated. Concerning the parallel

mode, a packet contains a diagonal of neurons, then

neurons are implicitly evaluated diagonal by diagonal.

Speedup

Task number

Speed up

Identity

Figure 6: Speed up factor versus number of tasks.

The experiment results show a signiﬁcant gain ob-

tained by our parallelization method. Moreover, the

number of iterations needed to reach a stable state is,

in some cases, decreased by this method.

The methods presented in Section II allow for im-

proving the sequential evaluation as well as the par-

allel evaluation, therefore, our speedup factor should

not be impacted. Combined with our approach, they

can further improve the evaluation time of the HNN

without affecting the convergence property.

7 CONCLUSIONS

We presented a parallelization method to improve the

convergence time of HNN to solve optimization prob-

lems. This approach has been applied on the schedul-

ing problem which can be easily deﬁned as an opti-

mization problem. The HNN associated to this prob-

lem has been built by adding several constraints (such

as k-outof-N rules) on some sets of neurons. We

demonstrated that the network convergence is main-

tained when a subset of disconnected neurons is eval-

uated in parallel. This means that when two neurons

do not belong to the same constraint, they can be eval-

uated in parallel. Because the construction of a HNN

based on the addition of several constraint rules is re-

ally common, we assume that this method can be used

for large number of optimization problems modelled

by HNNs.

The parallelization of neural evaluations leads to

an important improvement of the convergence time.

We have seen that on the task scheduling problem,

the speedup depends on the number of tasks. Thus,

for a scheduling problem with 20 tasks, the speedup

is about 25. Contrary to other works about parallel

evaluation of a HNN, our method preserves the con-

vergence property which permits to simplify the im-

plementation of a HNN.

REFERENCES

Del Balio, R., Tarantino, E., and Vaccaro, R. (1992). A par-

allel algorithm for asynchronous hopﬁeld neural net-

works. In IEEE International Workshop on Emerg-

ing Technologies and Factory Automation, pages 666

–669.

Domeika, M. J. and Page, E. W. (1996). Hopﬁeld neural

network simulation on a massively parallel machine.

Information Sciences, 91(1-2):133 – 145.

Hopﬁeld, J. and Tank, D. (1985). ”Neural” computation of

decisions in optimization problems. Biological cyber-

netics, 52(3):141–152.

Kamp, Y. and Hasler, M. (1990). Recursive neural networks

for associative memory. John Wiley & Sons, Inc.

ndziuk, J. (2002). Neural networks for the N-Queens

problem: a review. Control and Cybernetics,

31(2):217–248.

Sidney, J. (1977). Optimal single-machine scheduling with

earliness and tardiness penalties. Operations Re-

search, 25(1):62–69.

Smith, K. (1999). Neural Networks for Combinatorial Op-

timization: A Review of More Than a Decade of Re-

search. Informs Journal on Computing, 11:15–34.

Tagliarini, G., Christ, J., and Page, E. (1991). Optimization

using neural networks. IEEE Transactions on Com-

puters, 40(12):1347–1358.

Wang, C., Wang, H., and Sun, F. (2008). Hopﬁeld neu-

ral network approach for task scheduling in a grid en-

vironment. In Proceedings of the 2008 International

Conference on Computer Science and Software Engi-

neering - Volume 04, pages 811–814.

Wilson, R. C. (2009). Parallel hopﬁeld networks. Neural

Computation, 21:831–850.

Xu, Z., Hu, G., and Kwong, C. (1996). Asymmet-

ric Hopﬁeld-type networks: theory and applications.

Neural Networks, 9(3):483–501.

PARALLEL EVALUATION OF HOPFIELD NEURAL NETWORKS

253