EVALUATION OF THE EFFECT OF ND:YVO

LASER

PARAMETERS ON INTERNAL MICRO-CHANNEL

FABRICATION IN POLYCARBONATE

S. M. Karazi and D. Brabazon

School of Mechanical and Manufacturing Engineering, Dublin City University, Dublin, Ireland

Keywords: Pulsed Nd:YVO

laser, ANN, Factorial DoE, Predictive models, Channel dimensions, Polycarbonate.

Abstract: This paper presents the development of Artificial Neural Network (ANN) models for the prediction of laser

machined internal micro-channels’ dimensions and production costs. In this work, a pulsed Nd:YVO

laser

was used for machining micro-channels in polycarbonate material. Six ANN multi-layered, feed-forward,

back-propagation models are presented which were developed on three different training data sets. The

analysed data was obtained from a 3

factorial design of experiments (DoE). The controlled parameters

were laser power, P; pulse repetition frequency, PRF; and sample translation speed; U. Measured responses

were the micro-channel width and the micro-machining operating cost per metre of produced micro-

channel. The responses were sufficiently predicted within the set micro-machining parameters limits. Three

carefully selected statistical criteria were used for comparing the performance of the ANN predictive

models. The comparison showed that model which had the largest amount of training data provided the

highest degree of predictability. However, in cases where only a limited amount of ANN training data was

available, then training data taken from a Face Centred Cubic (FCC) model design provided the highest

level of predictability compared with the other examined training data sets.

1 INTRODUCTION

Laser micro-machining is a materials-processing

technique that uses precise laser energy per unit area

and per unit time in order to manage the thermal

field in the processed material with minimal thermal

damage and high precision. The material is in most

cases almost instantly brought up to melting

temperature and to vaporisation temperatures to

create the desired voxelated region of the micro-

machined channel. Laser micro-machining processes

include the drilling, cutting, milling and engraving

of materials with micro-dimensional tolerances.

Various statistical and numerical methodologies

have been implemented to predict and optimise

several laser manufacturing processes including

Artificial Neural Networks (ANN) (Lee et al. 2001);

Genetic Algorithms (GA) (Ye, Yuan and Zhou,

2009), Design of Experiments (DoE) (Karazi, Issa

and Brabazon, 2009), Finite Element Analysis

(FEA) (de Deus and Mazumder, 1996), Ant Colony

optimisation (AC) (Wang and Xie, 2005), and Fuzzy

Logic (FL) (Shen et al. 2006).

Due to their non-linear, adaptive and learning

ability using collected data, ANN models have been

successfully applied to a large number of problems

in several domain applications. Neural network

nodal functions can be evaluated simultaneously,

thereby gaining enormous increases in processing

speed (Collins and DeLucca, 2008, Neural

networks).

The prediction of the dimensions of the laser

micro-machining channels is an important

requirement for optimisation of the laser control

parameters. A Nd:YVO

laser micro-machining

system was previously used by the current authors

for the production of micro-channels (Karazi and

Brabazon, 2010) where it was shown that a wide

variety of desired geometries can be prepared.

ANN models were constructed and analysed to

test their predictive capabilities in this work. These

predictive models relate the input laser processing

parameters (power, traverse speed and pulse

repetition frequency) to the output responses

(machined channel width and micro-machining

cost). These ANN models may be used to select the

process input parameters which are required in order

254

M. Karazi S. and Brabazon D..

EVALUATION OF THE EFFECT OF ND:YVO4 LASER PARAMETERS ON INTERNAL MICRO-CHANNEL FABRICATION IN POLYCARBONATE.

DOI: 10.5220/0003683202540259

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 254-259

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

to achieve micro-channel dimensions within a

specified budget.

2 EXPERIMENTAL SET-UP

2.1 Experimental Work

In this paper, a 2W Nd:YVO

1064 nm wavelength

laser system was used for the micro-channel

fabrication. These internal micro-channels were

created in polycarbonate (PC) sheets of 10 mm

thickness. In order to facilitate the measurement of

the micro-channels’ widths, a 2 mm distance

between micro-channels was set. For micro-

machining, the PC work pieces were initially

positioned on the 3D positioning stage such that the

laser spot was focused beyond the sample surface.

The laser beam was then fired and the sample moved

away from the stationary laser head. This laser

micro-machining processing technique enabled

creating the internal micro-channel from the back to

the front of the sample

2.2 Experimental Design

In order to study the relationship between the main

Nd:YVO

laser process parameters and the

developed micro-channel width and corresponding

micro-machining operating cost, an arranged series

of information-gathering experiments was designed

according to DoE methodology.

In this paper, the examined laser process input

parameters were laser power, P; pulse repetition

frequency, PRF; and sample translation speed; U.

Each of these parameters was analysed at the low,

middle, and high levels, all of which were

determined after initial screening experiments. This

factorial design of experiments was prepared

using Design-Expert V7 software. The design levels

of the laser input parameters are shown in Table 1.

Table 1: Design of Experiment set levels of power, pulse

repetition frequency and sample speed used, as well as

corresponding level coding.

Variables P (W) PRF (kHz) U (mm/sec)

Low 0.5 13 0.5

Mid 1 23 1.74

High 1.5 33 2.98

There are 27 possible combinations of the three

process parameters at the three selected levels. The

centre point of the design was repeated five

additional times, where (P=1 W, PRF=23 kHz,

U=1.74 mm/sec), to provide a measure of process

stability and inherent variability.

2.3 Micro-channels Width

Measurement

The micro-channel width (diameter) for each

experiment was measured at three different locations

along the produced channel and the average values

were determined. Theses dimensional measurements

were carried out using Leica optical microscope and

OMNIMET image analysis software.

The measurement results of the repeated

experiments were averaged to one, bringing the

overall number of experiments from 32 to 27 unique

experiments. These measurement results (27 for

width and 27 for micro-machining cost) provided the

data set from which training sets were chosen for the

subsequent ANN modelling.

Table 2: Breakdown of estimated micro-machining cost per hour.

Element of cost Calculations Cost €/hr

Laser power supply

(800 W) (€0.16/kW hr) (P/2) / 1000 0.064×P

DELL PC Optiplex 170L & monitor (140 W)(€0.16/kW hr) / 1000 0.0224

CompactRIO - control power (8.2 W) (€0.16/kW hr) / 1000 0.0013

D-link network switch (4.5 W) (€0.16/kW hr) / 1000 0.0007

BWD MiniLab - motion power (43 W) (€0.16/kW hr) / 1000 0.0069

Diode replacement (€ 11,410 / 10000 hr) 1.141

Maintenance labour (12 hr/2000 hr operation) (€ 50/hr) 0.3

Total estimated micro-machining cost per hour 1.4723 + 0.064×P

Micro-machining cost [€/m] =

..×

€

(

.

)

×

















(..)



(1)

EVALUATION OF THE EFFECT OF ND:YVO4 LASER PARAMETERS ON INTERNAL MICRO-CHANNEL

FABRICATION IN POLYCARBONATE

255

2.4 Micro-machining Cost Calculation

Processing cost can be approximated as micro-

machining cost per length for a specific laser micro-

machining operation. In this approach, unplanned

maintenances and breakdowns have not been taken

into consideration. Furthermore, labour cost was not

considered since the Nd:YVO

laser was for

experimental purposes. Assuming the relationship

between the electrical consumption of the laser

power supply and the laser power emitted by the

laser head is linearly proportional, the total

estimated operating cost per hour as a function of the

output power can be expressed by 1.4723 +

0.064×P.

Table 2 shows a breakdown of estimated micro-

machining cost per hour. Assuming 85% utilisation,

the total approximated operating cost per unit length

(in €/m) is given by the following Equation (1).

2.5 ANN Models’ Setup

Three ANN predictive models were developed for

the width and another three for micro-machining

cost estimation using the three inputs P, U, and PRF.

These models were developed in order to examine

the influence of changing the number and the

selection of training data on the prediction capability

of the ANN model. These six models were based on

3 different training data sets as follows:

- Model I: 24 randomly selected experiments (from

the total of 27) were used to train the network;

- Model II: 14 experiments, selected according to the

Face Centred Cubic (FCC) Design, were used to

train the network;

- Model III: 13 experiments, selected according to

the Box-Behnken (BB) Design, were used to train

the network.

Figure 1: Schematic representation of the training data for (a) model I, (b) model II, and (c) model III.

(b) (c)

(a)

NCTA 2011 - International Conference on Neural Computation Theory and Applications

256

Each of these three models was used for two

models, one for the width prediction and another for

the operating cost per metre prediction. All 27

experimental data were employed for verification

purposes in order to locate the best ANN structure

within the various possible architectures for each

model. Figure 1 shows a representation of the

training data distribution in 3D space (a) for model I,

(b) for model II, and (c) for model III. The training

set of models II & III were selected according to two

popular designs; FCC Design and BB Design

respectively. These two designs were selected in

order to investigate which design should be chosen

in case only a limited number of experiments could

be performed. This scenario could occur when for

example carrying out the experiments is time

consuming, expensive, or dangerous.

2.6 Configuration of ANN Models

In this work, all the studied ANN models were of

feed-forward structure and back-propagation

algorithm. Moreover, they were designed and

executed using the aNETka software. Due to the

lack of a quantifiable procedure for theoretical

appraisal of the best ANN architecture, exhaustive

trial-and-error study was performed to find the best

ANN configuration for each model. Two ASCII text

input files were prepared for each model. The first

one contained the training data inputs and

corresponding outputs for the training stage. The

second one contained all 27 experimental data inputs

and their corresponding outputs for the verification

stage. In order to find the best ANN model, the

number of hidden layers was changed up to four and

the number of neurons in each hidden layer was

varied up to 100 neurons. A diagrammatic

description of the examined ANN architectures is

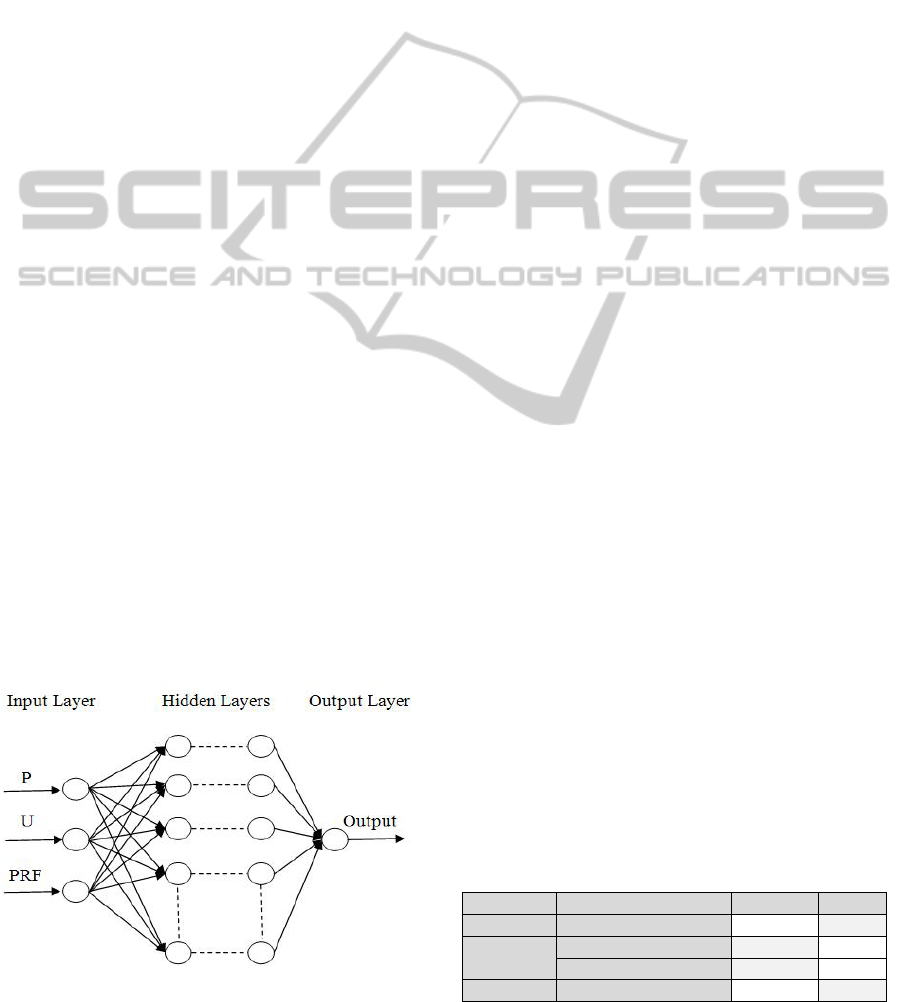
shown in Figure 2.

Figure 2: Architecture of feed-forward ANN schema

developed with three inputs and one output.

Due to its good generalisation capability, a

transfer sigmoid function was used in all

investigated ANN architectures. Since the learning

rate value controls the magnitude of weight and bias

updates, the choice of this value meaningfully

influences ANN schemas training time. Empirically

the learning rate value was manually varied between

0.0001 and 6 depending on the progress of the

aNETka execution during training process.

To avoid and reduce the probability of the

training runs being stuck in local optima, the

momentum parameter was utilised and fixed at a

medium value of 0.8 for all ANN training runs.

In the ANN program used the training data was

iteratively passed one by one through the ANN

structure and the weights were automatically

adjusted after each iteration. Part of the training data

was randomly selected and set aside by the aNETka

software in order to be used as a validation set and a

criterion to decide when to stop the training. In an

effort to minimise the training error and avoid over

training, the training process was supervised during

the ANN model formulation. The training part of the

aNETka software provided the user with a graphical

chart of the past and current RMS error value. This

graphical chart was ceaselessly supervised so that

ANN configurations with the highest prediction

capability could be obtained for each model.

Configurations for which the RMS errors raised

significantly and continuously during training were

dropped. Afterwards, the process of ANN structure

formation was restarted and only structures with

RMS error value below 0.001% were accepted.

3 RESULTS

3.1 Final ANN Structures

In this work and after trying a wide variety of hidden

layer diversifications, it was discovered that the best

ANN schemas were obtained with one or two hidden

layers. Table 3 shows the number of neurons in the

hidden layers that achieved best predictions of width

and cost for models I, II, and III.

Table 3: Number of neurons in the hidden layers for width

and depth in I, II, and III models.

Model Hidden layers width cost

I 1

6 4

3 4

3 -

III 1

8 4

EVALUATION OF THE EFFECT OF ND:YVO4 LASER PARAMETERS ON INTERNAL MICRO-CHANNEL

FABRICATION IN POLYCARBONATE

257

3.2 ANN Predictive Models’

Comparison

Comparison criteria are needed in order to quantify

the difference between values produced by a model

and the actual values. After a profound search in

statistics, three statistical estimators were found to

be the best criterions that together can do the

required work. These statistical estimators are MSE

(Mean Squared Error), R2 (The coefficient of

determination), and MAPE (Mean Absolute

Percentage Error). These estimators were employed

to provide a measure of how well future outcomes

are likely to be predicted by the investigated model.

Table 4 shows a side by side comparison between

models I, II, and III in terms of the three chosen

estimators.

The Mean Squared Errors (MSE), the

coefficients of determination (R

), and the Mean

Absolute Percentage Errors (MAPE) for width and

depth in I, II, and III models are shown in Table 4.

Lower values of MSE and MAPE and higher values

of R

indicate better model fit.

MSE, R

, and MAPE were calculated according

to the Formulas below:

MSE =



(

(



−y



)



)





(2)



=

∑

(





−

)



)





∑

(



−

)



)





(3)

MAPE =







−y











(4)

Where n is the number of experiments, y is the

actual value, and y is the predicted value,  is the

mean of actual values.

Practically these three estimators were used for

the selection of the best ANN schemas for each

model in the first place. Moreover, they were used to

compare the models I, II, and III.

4 DISCUSSION

In this work, factorial DoE assisted in the selection

of training data sets for the ANN predictive models.

Furthermore, it was found that ANN predictive

models have inherent capability to effectively re-

produce the outcomes of a nonlinear, complex and

dynamic system, like a laser micro-machining

system.

Ranking the models (I, II, and III) according to

the three statistical estimators, model I was the best

for width and cost responses. This might be

attributed to the great number of training data used

in this model (24 out of 27 available data). This was

the largest amount of training data compared to the

other models (14 for model II and 13 for model III).

This enabled model I to predict the whole

experimental data width and operating cost with a

small margin of error.

Model II was next best and better than model III,

even though both having almost the same number of

training data but different training data set. This

might be due to the fact that the training data set in

model II was chosen according to FCC Design

which covers all the corner points from the

experimental data space. While the rather worse

prediction of model IIIs that used BB Design, can be

comprehended when the absence of the eight

experimental data space corner points from the

training set is taken into account. So due to the lack

of these influential points, the estimation within the

data ranges will not be adequately exact from this

model.

It can be seen clearly from Table 4 that statistical

estimators for cost prediction are a lot better than

their counterparts for width prediction. This can be

attributed to the fact that production cost is

proportional to its inputs and it was originally

estimated using Equation (1). Furthermore, this

demonstrates the ability to utilise ANN as an

arbitrary function estimation technique that uses

experimentally observed data to “learn”.

Another notice from Table 4 that all statistical

estimators came to an agreement, model I was the

Table 4: Comparison criteria for width and depth models in I, II, and III models.

Estimator

Width

Estimator

Cost

I II III I II III

MSE 24.8 192.7 206.8 MSE 8x10

-11

9065x10

-11

273253x10

-11

0.99 0.95 0.95 R

0.99 0.99 0.99

MAPE 1.2 % 6.0% 7.2 % MAPE 0.003 % 0.038 % 0.100 %

NCTA 2011 - International Conference on Neural Computation Theory and Applications

258

best, model II the second, and model III the worst

with regards to both predictions, width and cost.

This indicates that these estimators work together in

harmony and have been well chosen. These results

empirically establish their use as criteria for

selecting both the best ANN configuration for a

developed model and the best model that describes a

system or a problem.

5 CONCLUSIONS

DoE was used to design an arranged series of

information-gathering experiments to characterise

micro-channel formation using a Nd:YVO

laser.

The relationship between the main laser process

parameters and the developed micro-channel width

and corresponding micro-machining operating cost

was examined using feed-forward, back-propagation

ANN predictive models. The influence of changing

the number and the selection of training data on the

prediction capability of the developed ANN

predictive model was investigated. MSE (Mean

Squared Error), R2 (The coefficient of

determination), and MAPE (Mean Absolute

Percentage Error) were utilised as a basis for

comparison between the developed ANN predictive

models.

The comparison showed that model I (which has

the highest number of training data) was the best.

Moreover, model II is better than model III (both

have almost the same number of training data but

different training data set). This indicates that the

more training data employed the better model fit

acquired. However, when limited number of

experiments (training data) is allowed, the outcomes

of this work favoured using FCC Design over BB

design for the selection of training data. This result

indicates that using FCC design for training data

selection was found more efficient in predicting

width and micro-machining cost and highlighted the

importance of including all experimental data space

corner points in any training data set. Moreover, this

comparison showed that the ANN modelling

technique can be smoothly employed to predict the

laser machined micro-channel dimensions and

production cost precisely.

Automated systems control can allow the use of

the models presented in this paper in order to

produce optimised micro-channels with high

dimensional precision and least production cost.

It was established in this work that the developed

ANN predictive models were efficient at satisfying

these demands and were effective for the prediction

of the most appropriate laser micro-machining

parameters.

REFERENCES

Collins, M. and DeLucca, M. 2011. Neural networks

[Online]. Available from: www.academic.marist.edu/

~jzbv/architecture/

Projects/S2002/NeuralNet2/COA.PPT, [accessed 27 July

2011].

de-Deus, A. M. and Mazumder, J. 1996. Two-

Dimensional Thermo-Mechanical Finite Element

Model for Laser Cladding, Laser Materials

Processing; Detroit, Michigan; USA, B174-B183

Karazi, S. M., Issa, A. and Brabazon, D. 2009.

Comparison of ANN and DoE for the prediction of

laser-machined micro-channel dimensions. Optics and

Lasers in Engineering, 47 (9), p. 956-964.

Karazi, S. M. and Brabazon, D. 2010. Analysis and

prediction of dimensions and cost of laser micro-

machining internal channel fabrication

process, International Symposium on Experimental

Mechanics ICEM14, Poitiers, France, EPJ Web of

Conferences, V 6, p. 25002.

Lee, S. H., Park, W.S., Cho, H. S., Zhang, W. and Leu, M.

C. 2001. A neural network approach to the modelling

and analysis of stereolithography processes,

Proceedings of the Institution of Mechanical

Engineers, Journal of Engineering Manufacture, 215,

p. 1719-1733.

Shen, H., Shi, Y. J.., Yao, Z. .Q and Hu, J. 2006. Fuzzy

logic model for bending angle in laser forming,

Materials Science and Technology, 22, p. 981-986.

Wang, G. G. and Xie, S. Q. 2005. Optimal process

planning for a combined punch-and-laser cutting

machine using ant colony, International Journal of

Production Research, 43, p. 2195 – 2216.

Ye, J., Yuan, X. C. and Zhou, G. 2003. Genetic algorithm

for optimization design of diffractive optical elements

in laser beam shaping, Proceedings of SPIE, 4594, p.

118-127.

EVALUATION OF THE EFFECT OF ND:YVO4 LASER PARAMETERS ON INTERNAL MICRO-CHANNEL

FABRICATION IN POLYCARBONATE

259