USING THE GNG-M ALGORITHM TO DEAL WITH THE

PROBLEM OF CATASTROPHIC FORGETTING IN

INCREMENTAL MODELLING

H´ector F. Satiz´abal M. and Andres Perez-Uribe

University of Applied Sciences of Western Switzerland (HEIG-VD), Del´emont, Switzerland

Keywords:

Catastrophic Interference, Incremental task, Incremental learning, Sequential learning, Growing neural gas.

Abstract:

Creating computational models from large and growing datasets is an important issue in current machine

learning research, because most modelling approaches can require prohibitive computational resources. This

work presents the use of incremental learning algorithms within the framework of an incremental modelling

approach. In particular, it presents the GNG-m algorithm, an adaptation of the Growing Neural Gas algorithm

(GNG), capable of circumventing the problem of catastrophic forgetting when modelling large datasets in a

sequential manner. We illustrate this by comparing the performance of GNG-m with that of the original GNG

algorithm, on a vector quantization task. Last but not least, we present the use of GNG-m in an incremental

modelling task using a real-world database of temperature, coming from a geographic information system

(GIS). The dataset of more than one million multidimensional observations is split in seven parts and then

reduced by vector quantization to a codebook of only thousands of prototypes.

1 INTRODUCTION

Building computationalmodels by means of inductive

inference has always been an important issue in sci-

ence. Current information systems gather information

in databases containing huge amounts of data, mak-

ing difﬁcult to tackle the problem of modelling by us-

ing traditional methods. Additionally, one must care

about the fact that, most of the time, these databases

continuously grow, thus requiring a dynamic mod-

elling approach being able to add new knowledge to

pre-existent models. As an example, consider mod-

elling a biological process, e.g., growth or develop-

ment. Biological processes change over time due to

the continuous variations on stimuli (e.g., climate).

Plants and animals behavedifferentdependingon sea-

sons, and seasons evolve through years depending on

more complex processes (e.g., global warming). This

is the intrinsic complexity of the problem, but this

scenario is reinforced by the fact that it is not pos-

sible to have all the concerned data in advance. In-

stead, the data are gradually collected in an incre-

mental way generating growing databases. Creating a

model of a such process each time new data are gen-

erated could imply large computation time because,

in a static modelling framework, the new model must

be created from scratch using the whole set of data.

A dynamic approach with growing models incorpo-

rating the information of new data is desirable in this

case.

An interesting approach which deals with this

kind of datasets is incremental modelling. This mod-

elling paradigm consists in considering the modelling

problem as an incremental task (Giraud-Carrier,

2000), and then using incremental learning tech-

niques in order to build a model from the available

data. Therefore, by using this approach, huge datasets

may be processed when they are still growing or, they

might be transformed by means of a sampling or par-

titioning procedure

before being fed to the incremen-

tal modelling framework.

This article presents the use of GNG-m, an adap-

tation of the popular GNG algorithm (Fritzke, 1995),

as a means for achieving incremental learning. More

speciﬁcally, the idea of the contribution is to use an

incremental modelling approach in order to process

huge datasets which would require too much mem-

ory and computation resources when using standard

batch approaches. The remainder of the article con-

tains the following sections. Section 2 introduces the

concept of incremental learning, gives some deﬁni-

By sampling or splitting the dataset the modelling task

is transformed in an incremental task.

267

F. Satizábal M. H. and Perez-Uriibe A..

USING THE GNG-M ALGORITHM TO DEAL WITH THE PROBLEM OF CATASTROPHIC FORGETTING IN INCREMENTAL MODELLING.

DOI: 10.5220/0003683702670276

In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 267-276

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

tions, and shows generalities of the approach. Section

3 explains the standard GNG algorithm, as well as the

modiﬁcations that were introduced in order to make

it more suitable for incremental modelling. Section 4

shows some tests of the performance of the algorithm

on a toy-set problem, and Section 5 presents the ap-

plication of the algorithm to a real-world large multi-

dimensional dataset. Finally, Section 6 draws some

conclusions about the approach of incremental mod-

elling in the task of processing huge databases, and on

the use of incremental learning algorithms like GNG

in this purpose.

2 INCREMENTAL MODELLING

The fact of having large or growingdatasets, while be-

ing positive and also desirable from the point of view

of a data acquisition system, constitutes a major draw-

back if the data are to be used in inductive modelling.

In the case of a huge database, one can devise two

possibilities. On the one hand, using huge amounts

of data to build models could be prohibitive because

of computational or storage constraints. And on the

other hand, taking only partial information from the

complete set and use it to build a model, implies the

use of special modelling paradigms being able to ap-

pend or insert new information into partial or growing

adaptive models.

A similar landscape is depicted if one thinks on

growing databases. It is a matter of fact that in order

to build an accurate model, a large enough amount of

data must be available. There are also two difﬁculties

here. On the one hand, it is not a trivial issue to know

beforehand the amount of data that is large enough for

building a model, and this is even more difﬁcult if the

data collecting process is still running. On the other

hand, suppose that the amount of gathered informa-

tion is large enough to build a model. In the case of

having a static process as modelling objective, those

data would be sufﬁcient to reach some level of accu-

racy. Conversely, if the model should ﬁt a dynamic

process, it would be better to have an adaptive mod-

elling framework that follows the changes of the pro-

cess, instead of having absolute stable models which

have to be rebuilt from scratch each time the process

changes. Again, a model structure that incrementally

changes with the amount and quality of data might be

a good strategy.

A modelling framework which fulﬁls the afore-

said requirements is incremental modelling, also

called incremental learning. In the area of ma-

chine learning, the term incremental learning has syn-

onymously been used with pattern learning and on-

line learning to describe the opposite of batch learn-

ing (Chalup, 2002). Within this context, it only means

to distinguish two policies for modifying the param-

eters of a model during training i.e., after the presen-

tation of each training example in the online case, or

after the cumulation of a certain number of modiﬁca-

tions in the batch case. We are considering a more

speciﬁc deﬁnition of the concept of incremental mod-

elling, which will be explained after deﬁning the con-

cept of incremental task in the next subsection.

2.1 Incremental Task

In general, modelling tasks where the examples or ob-

servations become available over time (usually one

at a time) are considered as incremental learning

tasks (Giraud-Carrier, 2000).

Traditional static methods can be employed for

building a model from an incremental task given that,

if there exist the possibility of waiting for the data,

any incremental learning task can be transformed into

a non-incremental one (Giraud-Carrier, 2000). This

approach has the hindrance of reaching excessive vol-

umes of data that could render infeasible the mod-

elling task. It would be preferable to make use of

the advantages of incremental learners in this case. In

the same way, a large non-incremental modelling task

being unbearable by traditional modelling approaches

can be transformed into an incremental task by sam-

pling or splitting the data, and then to use a incremen-

tal learner in order to build a model from the obtained

incremental dataset.

2.2 Incremental Learning

Besides being a synonym of pattern learning or on-

line learning in the machine learning terminology, in-

cremental learning is a concept which has been as-

sociated with learning processes where a standard

learning mechanism is combined with or is inﬂuenced

by stepwise adjustments during the learning process.

These adaptations can be changes in the structure

of the learning system (e.g., growing and construc-

tive neural networks), or changes in its parameters

(e.g., stochastic learning), or even changes in the con-

stitution of its input signals (e.g., order, complex-

ity) (Chalup, 2002). These adaptations have the pur-

pose of enabling the construction of more specialized

models by adding new information to the already ex-

istent knowledge, when it is available.

Within this context, incremental learning shares

the same meaning of sequential learning. In se-

quential learning, the learning system is sequentially

trained by using different datasets, which most of the

NCTA 2011 - International Conference on Neural Computation Theory and Applications

268

times are chunks of a larger dataset that grows due to

a gathering process which is still running. This deﬁni-

tion is very close to the concept of online learning, ex-

cept but the fact that in pure sequential learning each

dataset (and all related information) is discarded after

each step of the sequence. Only the model parameters

are kept

(Sarle, 2002).

Thus, as a conclusion, incremental modelling may

be deﬁned as the process of using any incremental

or sequential learning algorithm, to solve any incre-

mental learning task, even those which comes from

the transformation of non-incrementalones. This arti-

cle emphasizes on the use of incremental learning for

solving non-incremental tasks that were transformed

into incremental ones by means of a sampling or par-

tition procedure.

2.2.1 Stability - Plasticity Dilemma

Incremental learning algorithms must be designed to

remain plastic in response to signiﬁcant new events,

yet also remain stable in response to irrelevant events.

Moreover, it is desirable that, in the plastic mode

of the model, the new events affect only the part of

the model being concerned with the new knowledge

without causing interference with pre-existent con-

cepts. This compromise between stability and plastic-

ity (Grossberg, 1987; Carpenter and Grossberg, 1987)

is difﬁcult to achieve in static models with distributed

representations which try to minimize an objective

function. This phenomenonis due to the fact that sub-

sequent training datasets may have totally different

local minima, making the sequential training of suc-

cessive datasets to forget all previous sets, resulting

in the so called catastrophic interference (McCloskey

and Cohen, 1989). Several strategies has been pro-

posed in order to minimize these effects (French,

1994; Robins, 2004) in distributed representations.

Besides a distributed representation, information

can also be represented using a local scheme. Lo-

cal encoding of the information is one of the require-

ments to successfully perform learning in a sequential

manner (Sarle, 2002). The use of models with a local

representation of the information allows partial up-

dates of their parameters, permitting new knowledge

to be introduced into the model without modifying the

previous information already stored. Moreover, lo-

cal adaptations must be accompanied by the ability of

dynamically changing the model structure (i.e., grow-

ing), in order to give enough ﬂexibility when required.

In the particular case of artiﬁcial neural networks, these

parameters are the weighted connections between neurons

if knowledge is encoded in a distributed manner, or unit po-

sitions if the encoding schema is local.

3 THE GROWING NEURAL GAS

ALGORITHM

Growing Neural Gas (GNG) (Fritzke, 1995) is an

incremental point-based network (Bouchachia et al.,

2007) that performs vector quantization and topology

learning. The algorithm builds a neural network by in-

crementally adding units using a competitiveHebbian

learning strategy. The resulting structure is a graph of

neurons that reproduces the topology of the dataset by

keeping the distribution and the dimensionality of the

training data (Fritzke, 1997).

The classiﬁcation performance of GNG is com-

parable to conventional approaches (Heinke and

Hamker, 1998) but has the advantage of being incre-

mental. Hence, giving the possibility of training the

network even if the dataset is not completely available

all the time while reducing the risk of catastrophic in-

terference by using local encoding.

The algorithm proposed by Fritzke is shown in Ta-

ble 1. In this algorithm, every λ iterations (step 8)

one unit is inserted halfway between the unit q having

the highest error and its neighbour f having also the

highest error. Carrying out this insertion makes the

network to converge to a structure where each cell is

the prototype for approximately the same number of

data points and hence, keeping the original data dis-

tribution. The term “nearest unit” in step 2 refers to

the more widely used concept of best matching unit

(BMU).

−2 0 2 4 6 8 10

Figure 1: Two-dimensional Single-blob normal distribu-

tion.

As an example, a GNG network was trained using

the dataset shown in Figure 1, and the training param-

eters shown in Table 2. These values were selected af-

ter several runs of the algorithm. This dataset contains

10’000 observations drawn from a two-dimensional

normal distribution with means µ

= 5, µ

= 5 and

standard deviations σ

= 2, σ

= 2.

Figure 2 shows the position and distribution of

USING THE GNG-M ALGORITHM TO DEAL WITH THE PROBLEM OF CATASTROPHIC FORGETTING IN

INCREMENTAL MODELLING

269

Table 1: Original growing neural gas algorithm proposed by Fritzke.

Step 0: Start with two units a and b at random positions w

and w

in ℜ

Step 1: Generate an input signal ξ according to a (unknown) probability density function

P(ξ)

Step 2: Find the nearest unit s

and the second-nearest unit s

Step 3: Increment the age of all edges emanating from s

Step 4: Add the squared distance between the input signal and the nearest unit in input space

to a local counter variable:

∆error(s

) = kw

− ξk

Step 5: Move s

and its direct topological neighbours towards the input signal ξ by fractions

and ε

, respectively, of the total distance:

∆w

= ε

(ξ− w

)

∆w

= ε

(ξ− w

) for all direct neighbours n of s

Step 6: If s

and s

are connected by an edge, set the age of this edge to zero. If such an

edge does not exist, create it

Step 7: Remove edges with an age larger than a

max

. If the remaining units have no emanat-

ing edges, remove them as well

Step 8: If the number of input signals generated so far is an integer multiple of a parameter

λ, insert a new unit as follows:

• Determine the unit q with the maximum accumulated error.

• Insert a new unit r halfway between q and its neighbour f with the largest error

variable: w

= 0.5



+ w



• Insert edges connecting the new unit r with units q and f, and remove the

original edge between q and f.

• Decrease the error variables of q and f by multiplying them with a constant α.

Initialize the error variable of r with the new value of the error variable of q.

Step 9: Decrease all error variables by multiplying them with a constant d

Step 10: If a stopping criterion (e.g., net size or some performance measure) is not yet ful-

ﬁlled go to step 1

Table 2: Parameters for the Growing Neural Gas algorithm.

Parameter ε

λ a

max

α d

value 0.005 0.001 500 100 0.5 0.9

−2 0 2 4 6 8 10

Figure 2: Prototype vectors obtained with the GNG algo-

rithm using the whole dataset.

the 50 cells of the resulting structure. A smoothed

coloured density representation of the dataset from

where the prototypes were obtained was added to ev-

ery scatter plot in this paper. Showing the original

distribution of the training data can be useful to eval-

uate if the prototypes were correctly placed after the

learning process. As we can see in Figure 2, the dis-

tribution of each one of the variables is reproduced by

the group of prototypes in the network.

Now, in order to simulate the conditions that

would require the use of incremental modelling, let

us consider this dataset to be so huge that it is impos-

sible to be processed in one single step due to memory

constraints. Then, incremental modelling arises as a

possible solution to overcome this problem. The huge

dataset can be split, transforming the task of mod-

elling into an incremental one, and then one can use

an incremental learner (e.g., the GNG algorithm) to

build a model of the dataset in a sequential manner.

Figure 3 shows the resulting positions of the pro-

NCTA 2011 - International Conference on Neural Computation Theory and Applications

270

totypes of the GNG network after doing a sequential

training with the split version (2 parts) of the dataset

shown in Figure 1. As it can be seen, after the ﬁrst

step of the sequence, the algorithm reproducesthe dis-

tribution of the ﬁrst part of the dataset without any

problem. Then, after presenting the second part, the

algorithm “forgets” the ﬁrst part (i.e., the quantization

error for this part increases), assigning some of the

prototypes that represented the ﬁrst part of the data to

the more recent second part of the dataset. This unde-

sirable manifestation of catastrophic forgetting is due

to the fact that the algorithm, being pure incremen-

tal, does not keep information about previous datasets

used to train the network, and therefore, there is no

way of knowing if one of the units of the network rep-

resented some important data, and that given this fact

its position must remain invariable.

−2 0 2 4 6 8 10

(a) Step 1

−2 0 2 4 6 8 10

(b) Step 2

Figure 3: Prototypes generated with the sequential training

of a GNG from a dataset split in two parts.

In order to minimize the aforementioned situation,

one modiﬁcation to the original algorithm is proposed

in Section 3.1.

3.1 The GNG-m Algorithm

The original version of the GNG algorithm does not

keep any additional information about the observa-

tions that have been presented to the network; only

unit positions and edge ages are stored in the model.

This policy, while making the algorithm suitable for

performing incremental learning (pure sequential al-

gorithm), does not allow the algorithm to know if a

unit in the graph has been an important prototype (i.e.,

a best matching unit) in previous runs.

The idea of the GNG-m algorithm is to attenuate

parameters ε

and ε

of the original version (which

represent the change of position of the units) for the

units which have been useful for representing obser-

vations previously presented to the network. In order

to do that, we associated a property of “mass” to each

unit in the network, in a way that units having been

useful for quantizing the dataset get more mass than

units representing less data. Hence, we adapted step 5

to take into account the mass value of the unit, freeing

“lighter” units and locking the “heavier” ones.

In summary, the proposed modiﬁcation adds two

parameters, massInc, and massDec, to the original

GNG algorithm. Each time a unit is selected as the

nearest unit s

, its mass is incremented by massInc,

while all its direct neighbours decrease their mass by

massDec. The mass of the unit is then used to mod-

ulate how far a unit can move in a single step, and as

a result, units having been selected more often as the

nearest unit change less their position than units that

represent less points in the dataset.

−2 0 2 4 6 8 10

(a) Step 1

−2 0 2 4 6 8 10

(b) Step 2

Figure 4: Prototypes generated with the sequential training

of a GNG-m from a dataset split in two parts.

As an example, Figure 4 shows the resulting po-

sitions of the prototypes of the GNG-m network after

doing a sequential training with the split version (2

parts) of the dataset shown in Figure 1. Contrary to

the results shown in Section 3, the modiﬁed version

of the algorithm satisfactorily places new prototypes

when the second part of the ﬁle is presented, with-

out modifying the positions of the prototypes repre-

senting the ﬁrst part. More examples using this new

algorithm are given in the next section.

4 TOY-SET EXPERIMENTS

This section shows the results of several tests using

the dataset shown in Figure 1. Two approaches for

modelling a huge dataset are compared i.e., model

merging and incremental modelling. In the case of

model merging, we explored parallel and cascade

merging. For the incremental modelling approach, we

used both versions of the GNG algorithm presented in

Section 3 and Section 3.1.

In the case of this toy-set, it is possible to train a

model with the whole database. Thus, in order to have

a reference to compare with, the resulting prototypes

when using the whole dataset are shown in Figure 2.

The dataset used for the tests has only 10’000 ob-

servations; however, we used it in order to simulate a

huge one which cannot be loaded in memory. In order

USING THE GNG-M ALGORITHM TO DEAL WITH THE PROBLEM OF CATASTROPHIC FORGETTING IN

INCREMENTAL MODELLING

271

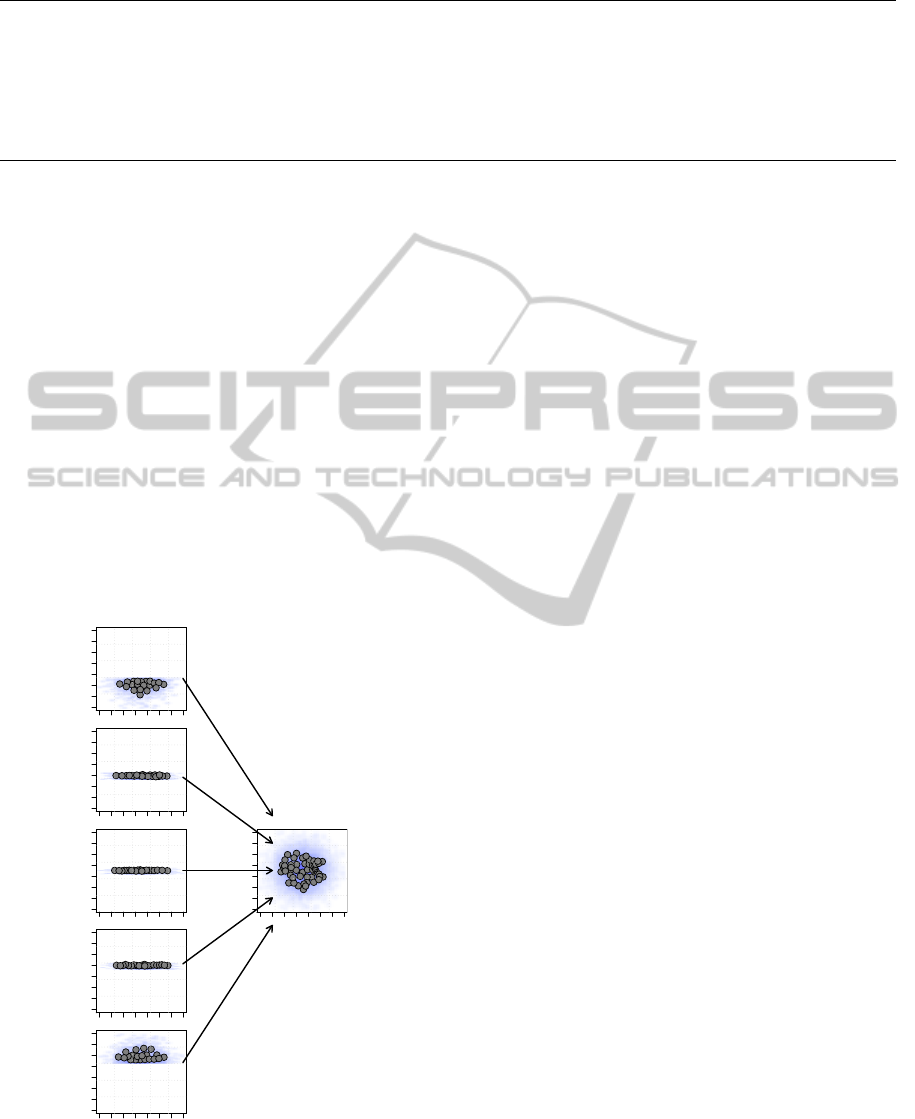
Table 3: Proposed modiﬁcation to the original algorithm.

Step 5: Move s

and its direct topological neighbours towards the input signal ξ by fractions

and ε

, respectively, of the total distance:

∆w

= (ε

· e

mass

)(ξ− w

)

∆w

= (ε

· e

mass

)(ξ− w

) for all direct neighbours n of s

mass

= mass

+ massInc

mass

= mass

− massDec for all direct neighbours n of s

to do that, this toy-set was split in ﬁve and four parts

by using different patterns (vertical and tangential re-

spectively).

4.1 Splitting the Dataset in Five Parts

In this ﬁrst group of experiments the dataset was ver-

tically split in ﬁve parts, and each part was used to

build a quantized version of the whole set of observa-

tions in an incremental manner.

4.1.1 Parallel and Cascade Merging

The ﬁrst approach we explored for accomplishing the

task of building a quantized version of the split dataset

is to train small individual models with each part, and

then to use the resulting prototypes as inputs for train-

ing a ﬁnal neural network. This ﬁnal model should

reproduce the distribution of the whole dataset.

−2 2 4 6 8 12

Figure 5: Prototypes of a GNG after a parallel merging of

ﬁve sets of pre-computed prototypes.

Figure 5 shows the results of training ﬁve mod-

els (i.e., one model for each one of the parts of the

dataset), and then merging the resulting models into

one single ﬁnal model. This merging is done by tak-

ing the positions of all the units in the ﬁve neural net-

works, and using them as inputs to train a ﬁnal net-

work with the GNG algorithm. As it can be seen, the

position of the units of the ﬁnal model reproduces the

input data distribution.

However, this procedure we called parallel merg-

ing, only emulates partially our subject of interest.

The ﬁnal model can be trained only after having built

each one of the smaller models, or in other words, the

whole dataset must be available in order to have a ﬁ-

nal model reproducing the distribution of the data.

Besides the parallel approach for merging the par-

tial models, we tested a cascade strategy. In this case,

a new up-to-date model is incrementally trained each

time a new part of the dataset is available. There-

fore, a new input dataset must be compiled at each

step of the merging strategy by appending the result-

ing prototypes of the previous step, and the incoming

data. This growing dataset is employed for building

the model at each step.

Figure 6 shows the results of quantizing the pro-

posed dataset by using a cascade merging approach.

As it can be seen in Figure 6(a), the fact of combin-

ing a quantized version of the partial dataset (i.e., the

positions of the units of the last model) with the in-

coming data, does not produce a correct representa-

tion of the whole dataset. The distribution of units in

the GNG algorithm depends strongly on the density of

points in the input dataset. The algorithm distributes

its units in a way that every unit in the network is

a prototype for approximatively the same amount of

data points (i.e., entropy minimization). Hence, the

algorithm gives more importance to the more popu-

lated incoming dataset and tends to “forget” the infor-

mation of the less populated set of prototypes of the

last available model. Figure 6 shows the quantization

error after each step of the cascade merging. As it can

be seen in Figure 6(b), the quantization error of the

ﬁrst part increases after the presentation of new parts

of the dataset.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

272

−2 2 6 10

Step 2

−2 2 6 10

Step 3

−2 2 6 10

Step 4

−2 2 6 10

Step 5

(a) Cascade merging

1 2 3 4 5

0 1 2 3 4 5 6

Part 1

Part 2

Part 3

Part 4

Part 5

Steps

Average SSE

Quantization error

(b) Quantization error

Figure 6: Prototypes of a GNG after a cascade merging of a dataset split in ﬁve parts.

−2 0 2 4 6 8 10

(a) Step 1

−2 0 2 4 6 8 10

(b) Step 2

−2 0 2 4 6 8 10

(d) Step 4

−2 0 2 4 6 8 10

(e) Step 5

Figure 7: Prototypes generated with a sequential training of a GNG from a dataset split in ﬁve parts.

−2 0 2 4 6 8 10

(a) Step 1

−2 0 2 4 6 8 10

(b) Step 2

−2 0 2 4 6 8 10

(d) Step 4

−2 0 2 4 6 8 10

(e) Step 5

Figure 8: Prototypes generated with a sequential training of a GNG-m from a dataset split in ﬁve parts.

4.1.2 Incremental Modelling with the GNG and

GNG-m Algorithms

In this section we employed the incremental approach

for building a quantized version of the dataset split in

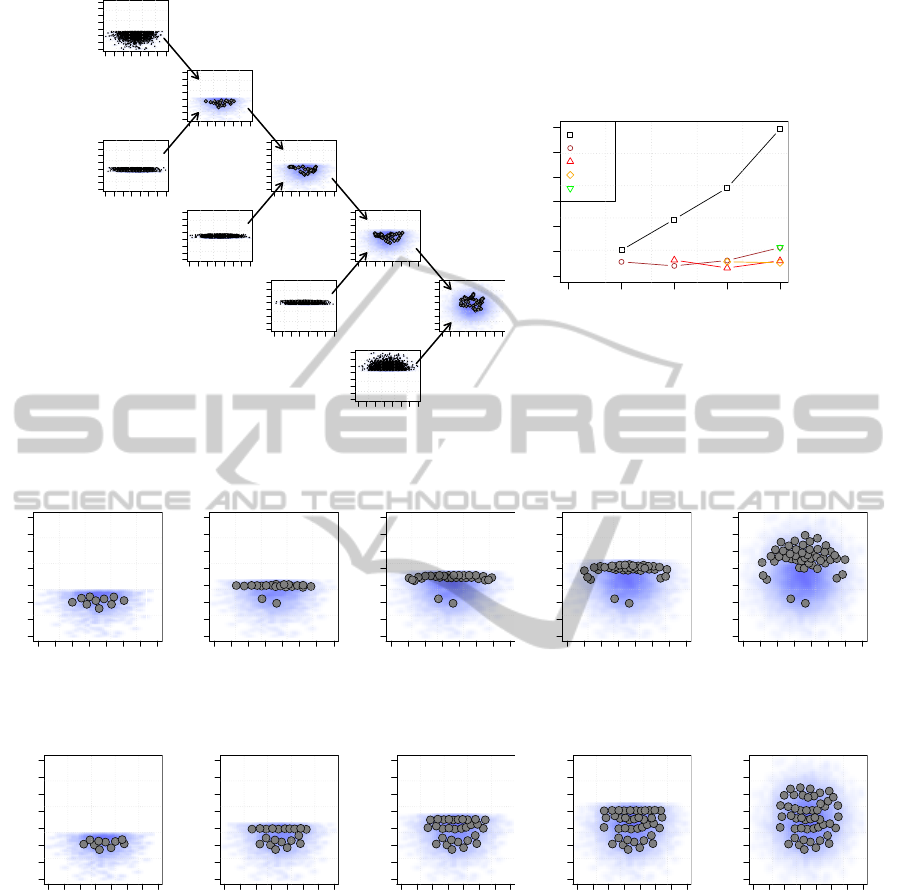
ﬁve parts. Figure 7 shows the resulting prototypes

when the dataset is sequentially quantized by using

the original GNG algorithm. As it was already dis-

cussed in section 3, the former parts of the dataset are

lost after presenting the last ones because there is no

information about how useful each unit is in the net-

work.

Figure 9 shows the quantization error for each part

of the dataset after each step of the sequential learning

process. As it can be seen in ﬁgure 9(a), the quantiza-

tion error of the former parts increases when the latter

parts of the dataset are presented.

As it was mentioned in Section 3.1, the prob-

lem of catastrophic forgetting can be solved by us-

ing the GNG-m algorithm. Figure 8 shows the result-

ing prototypes after sequentially training a GNG-m

algorithm with the dataset split in ﬁve parts. As it

USING THE GNG-M ALGORITHM TO DEAL WITH THE PROBLEM OF CATASTROPHIC FORGETTING IN

INCREMENTAL MODELLING

273

−2 0 2 4 6 8 10

(a) Step 1

−2 0 2 4 6 8 10

(b) Step 2

−2 0 2 4 6 8 10

(d) Step 4

Figure 10: Prototypes generated with a sequential training of a GNG from a dataset split in four parts.

−2 0 2 4 6 8 10

(a) Step 1

−2 0 2 4 6 8 10

(b) Step 2

−2 0 2 4 6 8 10

(d) Step 4

Figure 11: Prototypes generated with a sequential training of a GNG from a dataset split in four parts.

1 2 3 4 5

0.0 0.5 1.0 1.5 2.0 2.5

Part 1

Part 2

Part 3

Part 4

Part 5

Steps

Average SSE

Quantization error

(a) Using GNG

1 2 3 4 5

0.0 0.5 1.0 1.5 2.0 2.5

Part 1

Part 2

Part 3

Part 4

Part 5

Steps

Average SSE

Quantization error

(b) Using GNG-m

Figure 9: Average quantization error for each one of the

parts at each step after a sequential training of a dataset split

in ﬁve parts.

can be seen, the policy of locking units according to

its relative relevance (mass of the neurons) makes the

algorithm to insert new units where needed, without

modifying units which were useful for representing a

previous subset.

Figure 9 shows the difference between both ver-

sions of the algorithms in terms of the quantization

error of each one of the parts of the dataset. As it can

be seen inFigure 9(b), the quantization error remains

almost constant in the case of the GNG-m algorithm,

whereas the GNG algorithm makes it to continuously

increase.

4.2 Splitting the Dataset in Four Parts

This section shows the results of testing the method-

ology by using a version of the dataset which was tan-

gentially split in four parts. This splitting pattern al-

lowed us to test how the algorithm behaves when data

points close to a former distribution are presented in

later stages of the learning sequence. Only results

concerning the incremental modelling approach are

shown in this section.

Figure 10 shows the positions of the resulting pro-

totypes after sequentially applying the original GNG

algorithm to the dataset split in four parts. As it can be

seen, the model loses completely the prototypes rep-

resenting the ﬁrst part of the dataset after presenting

the last one. Conversely, Figure 11 shows the posi-

tions of the resulting prototypes after using the GNG-

m version of the algorithm. As it can be seen, the

modiﬁed version of the algorithm manages to keep

the information of the ﬁrst part even after presenting

the last part of the dataset. Figure 12 shows the dif-

ference in the behaviour of both versions in terms of

the quantization error of each part of the dataset, after

each step of the sequence.

As it can be seen in Figure 12(b), the quantization

error in the GNG-m version of the algorithm remains

almost constant, reducing catastrophic forgetting in

incremental modelling.

5 USING A REAL-WORLD

DATASET

In order to further validate the incremental modelling

approach, and to give an idea of a real application, we

NCTA 2011 - International Conference on Neural Computation Theory and Applications

274

1.0 1.5 2.0 2.5 3.0 3.5 4.0

0.0 0.5 1.0 1.5 2.0 2.5 3.0

Part 1

Part 2

Part 3

Part 4

Steps

Average SSE

Quantization error

(a) Using GNG

1.0 1.5 2.0 2.5 3.0 3.5 4.0

0.0 0.5 1.0 1.5 2.0 2.5 3.0

Part 1

Part 2

Part 3

Part 4

Steps

Average SSE

Quantization error

(b) Using GNG-m

Figure 12: Average quantization error for each one of the

parts at each step after sequential training of the GNG and

GNG-m algorithms with a dataset split in four parts.

quantized a real large multidimensional dataset using

both versions of the GNG algorithm.

The dataset we used comes from the climate

database WORLDCLIM (Hijmans et al., 2005), and

contains information of the current conditions of tem-

perature in Colombia (averaged from 1950 to 2000).

There are 1’336’025 observations, each one corre-

sponding to one pixel with a spatial resolution of one

square kilometre. Each observation has 36 dimen-

sions i.e., maximum temperature for the 12 months of

the year, minimum temperature for the 12 months of

the year, and averagetemperature for the 12 months of

the year. The goal with this dataset is to build a quan-

tized version with a reduced number of prototypes,

which can be analysed faster than taking the whole

set of observations. The resulting set of prototypes

could be useful for ﬁnding homologue regions within

the country, or for ﬁnding species distributions.

The ﬁrst step of the process consists in transform-

ing the task of vector quantization into an incremen-

tal task. Thus, the dataset was split in 7 parts

, six

parts with 200’000 observations, and one last part

with 136’025 observations. These parts were used

for sequentially training the GNG models. The sec-

ond step in incremental modelling consists in creat-

ing a model from the data by using an incremental

learner algorithm. For this application we did not use

exactly the original version of the GNG algorithm,

but a slightly modiﬁed version (Satiz´abal et al., 2009)

which prevents the accumulation of prototypes when

the dataset is highly heterogeneous. The parameters

we used to quantize the data can be found in Table 4.

The resulting prototypes can not be easily visu-

alised given that the dataset has 36 dimensions. In-

stead, in order to illustrate the difference between

both versions of the algorithm, Figure 13 shows the

quantization error of each part of the dataset during

The splitting pattern was only geographic, from north

to south, without taking into account the properties of the

dataset in the space of features.

all the steps of the sequence of learning. When us-

ing the standard GNG algorithm, the error of the ﬁrst

parts increases after presenting the subsequent parts

of the dataset. These changes in the quantization error

reveal that catastrophic forgetting is occurring during

learning. Or in other words, that units which were in-

troduced in the network in order to quantize a speciﬁc

region of the data distribution, are then reallocated to

new regions, causing the quantization error of the for-

mer parts to increase.

This situation is alleviated by the modiﬁcations

proposed in Section 3.1. As it can be seen in Fig-

ure 13(b), when the GNG-m version is used, the quan-

tization error of each part of the dataset remains al-

most constant during the subsequent steps of learn-

ing. Instead of moving pre-inserted units, the algo-

rithm inserts new units for the new regions, and keeps

the existing ones in order to maintain the knowledge

in the network.

6 CONCLUSIONS

Incremental modelling consists in using incremental

learning algorithms for building models from data

coming from incremental tasks. These incremental

tasks can be incremental per se (i.e., where observa-

tions are available one at the time), or can be created

from non-incremental ones by using partition or sam-

pling procedures. This strategy is useful when one has

to deal with large and/or growing databases. In the

case of a large database where all the data are avail-

able, a sampling or partition procedure can be used

to divide the whole dataset into smaller parts. These

sub-sets can be used either for building small models

which have to be merged into one single ﬁnal model

by using parallel merging, or for feeding an incremen-

tal learner which must deal with the construction of an

incremental model. Partition and sampling are only

possible if the whole dataset is available. In the case

of growing databases, the data have to be accumulated

to form chunks of data that can be presented sequen-

tially to the incremental learner. In this manner, an

up-to-date model is always available as the result of

training the last generated model with the more re-

cent data. A merging strategy is not feasible in this

case (see Section 4).

In the case of this contribution, we used the

Growing Neural Gas (GNG) algorithm as incremental

learner to explore the possibility of quantizing a large

dataset in an incremental manner. The original algo-

rithm (Fritzke, 1995) was slightly modiﬁed by adding

two parameters which control the plasticity of the net-

work. In the modiﬁed version (GNG-m), each unit in

USING THE GNG-M ALGORITHM TO DEAL WITH THE PROBLEM OF CATASTROPHIC FORGETTING IN

INCREMENTAL MODELLING

275

Table 4: Parameters for the Growing Neural Gas algorithm.

Parameter ε

λ a

max

α d hold sup

value 0.05 0.005 250 1000 0.5 0.9 0.1 10%

0 1 2 3 4 5 6 7

0.03 0.05 0.07 0.09

Part 1

Part 2

Part 3

Part 4

Part 5

Part 6

Part 7

Steps

Average SSE

Quantization error

(a) Using GNG

0 1 2 3 4 5 6 7

0.03 0.05 0.07 0.09

Part 1

Part 2

Part 3

Part 4

Part 5

Part 6

Part 7

Steps

Average SSE

Quantization error

(b) Using GNG-m

Figure 13: Average quantization error for each one of the parts at each step.

the network has information of how many times the

unit has been selected as the nearest unit of any ob-

servation in the dataset. We call this information the

mass of the unit. In this way, units having a smaller

mass can move more easily than units having a larger

mass. The tests we performed showed how these new

parameters can be useful in alleviating the problem of

catastrophic forgetting in incremental learning.

However, these modiﬁcations to the algorithm do

not consider the possibility of building models from

data coming from dynamic systems. The GNG-m al-

gorithm can increase the property of memory, which

represents stability, but at the same time decreases the

plasticity of the network. Increasing stability is de-

sired in the case of modelling a large dataset because

catastrophic forgetting is undesirable. Conversely,

forgetting becomes an important feature when the

process generating the data changes over time. In this

case, a policy such as “mass-decay” can be a feasi-

ble approach to control the ability of the network to

forget the oldest events, and thus remaining plastic to

capture the changing dynamics of the process being

modelled.

REFERENCES

Bouchachia, A., Gabrys, B., and Sahel, Z. (2007).

Overview of some incremental learning algorithms. In

Proceedings of the Fuzzy Systems Conference, 2007.

FUZZ-IEEE 2007, pages 1–6.

Carpenter, G. A. and Grossberg, S. (1987). Art 2: self-

organization of stable category recognition codes for

analog input patterns. Appl. Opt., 26(23):4919–4930.

Chalup, S. K. (2002). Incremental learning in biological

and machine learning systems. Int. J. Neural Syst.,

12(6):447–465.

French, R. M. (1994). Catastrophic forgetting in connec-

tionist networks: Causes, consequences and solutions.

In Trends in Cognitive Sciences, pages 128–135.

Fritzke, B. (1995). A growing neural gas network learns

topologies. In Advances in Neural Information Pro-

cessing Systems 7, pages 625–632. MIT Press.

Fritzke, B. (1997). Unsupervised ontogenic networks. In

Handbook of Neural Computation, chapter C 2.4. In-

stitute of Physics and Oxford University Press.

Giraud-Carrier, C.(2000). A note on the utility of incremen-

tal learning. Aicommunications, 13(4):215–223(9).

Grossberg, S. (1987). Competitive learning: From interac-

tive activation to adaptive resonance. Cognitive Sci-

ence, 11(1):23 – 63.

Heinke, D. and Hamker, F. H. (1998). Comparing neural

networks: a benchmark on growing neural gas, grow-

ing cell structures, and fuzzy ARTMAP. IEEE Trans-

actions on Neural Networks, 9(6):1279–1291.

Hijmans, R. J., Cameron, S. E., Parra, J. L., Jones, P. G., and

Jarvis, A. (2005). Very high resolution interpolated

climate surfaces for global land areas. International

Journal of Climatology, 25(15):1965–1978.

McCloskey, M. and Cohen, N. J. (1989). Catastrophic in-

terference in connectionist networks: The sequential

learning problem. In Bower, G. H., editor, The Psy-

chology of Learning and Motivation: Advances in Re-

search and Theory, volume 24, pages 109–136. Aca-

demic Press inc.

Robins, A. (2004). Sequential learning in neural networks:

A review and a discussion of pseudorehearsal based

methods. Intell. Data Anal., 8(3):301–322.

Sarle, W. S. (2002). comp.ai.neural-nets faq - part 2. Avail-

able: http://www.faqs.org/faqs/ai-faq/neural-nets/part2/.

Satiz´abal, H. F., Perez-Uribe, A., and Tomassini, M. (2009).

Avoiding prototype proliferation in incremental vector

quantization of large heterogeneous datasets. In Con-

structive Neural Networks, pages 243–260. Springer

Berlin / Heidelberg.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

276