A FUZZY LOGIC MODEL FOR NETWORK SIGNAL CONTROL

AND TRANSIT PREEMPTION

Yaser E. Hawas

Civil and Environmental Engineering Department, UAE University, Al Ain, U.A.E.

Keywords: Signal control, Fuzzy logic modelling and control, Simulation, Transit pre-emption.

Abstract: The majority of the fuzzy controllers for traffic signal control in the literature operate using raw data from

single point detectors installed on the intersection’s various approaches. The input variables to the fuzzy

logic controllers are usually simple estimates of traffic measures such as flow, speed or occupancy,

estimated from such single detector readings. A room for improvement is sought herein by developing a

fuzzy logic model (FLM) that could be integrated with smarter “processing” tools to estimate several traffic

measures from multiple detectors on each approach. The estimates obtained from this processing tool are

integrated as input knowledge into the FLM. The devised FLM structure is presented. A mesoscopic

simulation model is devised to test the effectiveness of the FLM. The premise of the presented FLM is that

it accounts for the network congestion downstream the individual traffic signals. This makes the FLM

applicable for network rather than isolated type of signal control. Furthermore, the FLM accounts for transit

pre-emption control as warranted. Several simulation-based experiments are presented including the basic

FLM for isolated signal control, the FLM control enabling downstream congestion effect, and the one

enabling transit pre-emption. The results are presented and discussed in details.

1 INTRODUCTION

Fuzzy logic models and artificial intelligence

methodologies were reported to have promising

capabilities to deal with highway traffic network

problems. Some fuzzy logic applications for traffic

modeling and control were developed using some

intuitive approaches based on capturing the

knowledge of the operators or experts (Sugeno and

Nishida, 1985). More applications were developed

using heuristic design rules or on-line adaptation of

initially intuited rules (Zimmermann, 1996). Several

FLM applications for traffic signal control were

discussed in (Niittymaki and Pursula, 2000). A

multi-level FLM coupled with a reasoning approach

was used in (Niittymaki and Turunen, 2003).

Multiple upstream detectors were used to measure

flows and estimate queues. The traffic flows are

used to estimate the approaches’ traffic intensities,

which are then used to decide on extension or

termination of the current phase green using a two-

stage FLM (Triba et al., 1999).

Fuzzy logic has been occasionally criticized

because the membership functions and the

knowledge base (rules) are conventionally set

intuitively using reasoning arguments of huge data

sets or trail-and-errors. As such, optimal

performance is not guaranteed. To overcome these

deficiencies, the neuro-fuzzy logic approach

(integrated fuzzy logic and neural nets) had emerged

in literature as a promising approach in controlling

complex systems by utilizing the training

capabilities of the neural nets (Hawas, 2007).

Among the initial attempts for neuro-fuzzy logic

applications for traffic signal control is the work

reported in (Henry et al., 1998). The use of neural

nets in learning [through simulation data] the best

detector location as it relates to the signal delay is

discussed in (Bingham, 2001). A set of simplified

simulation experiments were developed to assess the

performance and to illustrate the training of the

FLM.

Simulation is recognized in literature as the tool to

assess the effectiveness of the devised fuzzy logic

models (Chou and Teng, 2003); (Kosonen, 2003);

(Murat and Gedizlioglu, 2005). Simulation was also

adopted together with multi-agent control scheme,

and fuzzy inference (Kosonen, 2003). Each signal

operates individually as an agent, negotiating with

other agents (signals) about the control strategy

451

E. Hawas Y..

A FUZZY LOGIC MODEL FOR NETWORK SIGNAL CONTROL AND TRANSIT PREEMPTION.

DOI: 10.5220/0003685704510458

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FCTA-2011), pages 451-458

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

(Kosonen, 2003).

The majority of the fuzzy logic controllers in the

literature depend on raw counting detector data, with

very few attempts (Palacharla and Nelson, 1999);

(Mirchandani and Head, 2001); (Wen, 2007) made

to transfer such data into other traffic measures that

could be used to enhance the control intuition and/or

effectiveness. Fuzzy logic and neural nets were

utilized to estimate the link travel time (Palacharla

and Nelson, 1999). A real-time traffic control system

that predicts traffic measures [such as travel time,

queue spillbacks, and turning probabilities to enable

pro-active control] was introduced in (Mirchandani

and Head, 2001). A framework for dynamic traffic

light control coupled with a simulation model [to

analyze the inter-arrival and inter-departure times to

estimate the essential traffic measures needed for the

control logic] was introduced in (Wen, 2007).

In summary, the limitations of the fuzzy systems

for traffic control include the little consideration to

the effect of the traffic stream composition (small

cars, vans, trucks, buses, etc). Literally there is no

consideration for transit vehicles preemptions.

Among the limitations also is that the traffic

congestion in the downstream of the signal

approaches is not accounted for, and as such green

time might not be effectively allocated to a phase

(based on its upstream detector counts) in situations

where the downstream approaches are exhibiting

extreme congestion or blockage. Furthermore, little

was reported on how the actual or the predicted

queue on the approaches can be accurately

estimated, as it cannot be detected by the typical

single loop detector arrangement.

The majority of the fuzzy logic controllers in the

literature are reactive to the raw detector data

(counts) on the signal approaches. For instance,

almost all the reported controllers depend on point

detector “vehicular” counts with no considerations

for vehicular types. Treating all types of vehicles

equally might not result in fair treatment of all

phases, if the traffic stream composition is varying

among the phases. An approach with high

percentage of heavy vehicles or busses should not be

treated as equal as another approach with similar

flows of small cars only. A better treatment is to

account for the passenger car units flow instead of

the vehicular flow. Alternatively, one could also

devise a controller to preempt the public busses.

Furthermore, the raw vehicular counts do not

explicitly capture the congestion status along the

approaches. Incorporating additional variables such

as concentration, actual approach speed, or queue

length would result in a better logic. As a rule of

thumb, a single point detector on each approach is

not enough to capture the congestion status of the

approach. Furthermore, a logic that depends on one

traffic measure (such as flow) could employ

erroneous decisions.

A more effective controller is sought herein by

integrating the envisaged FLM to a processing tool

of the raw data. This tool is intended to process the

raw data into knowledge to develop smarter logic.

The knowledge processing tool would utilize the

detector counts to estimate some input variables to

the FLM. In this paper, a fuzzy signal controller that

incorporates “knowledge” in the decision making

process and not merely raw detector data is

developed. “Knowledge” term refers to any traffic

measures estimated from raw data.

2 OVERVIEW OF FUZZY LOGIC

SYSTEM

The developed FLM system requires the installation

of two detectors for each lane (one downstream, and

one upstream). This is the minimum requirement

needed to accurately capture the congestion status of

the approach. Additional detectors might be installed

to increase the accuracy of estimating some traffic

measures such as queue length, but this may be

argued to be cost ineffective. For simplicity in

presentation, we assume that the FLM is operating a

four-phase signal; each approach is assigned a

separate phase.

The logic depends on the (passenger car units)

PCU estimates on each approach. This takes into

account the traffic stream composition and the

turning movement percentages (captured by the

detectors). The field detectors’ readings are

processed further by some traffic status estimator

tool, that transfer such field measures into complex

traffic measures (or “knowledge”), which are then

used as inputs to the FLM. The knowledge here

refers to the estimated traffic measures beyond the

field detector counts. The introduced FLM utilizes

the estimates of the following traffic measures for

each phase’s approach:

• Traffic counts on approach in PCU

• Queue length (count) on approach in PCU

• Truck percentage

• Average approach speed

• Downstream link blockage index; an index (1-

100) to indicate the congestion status of the

downstream link (100% indicating a fully blocked

downstream link)

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

452

• A transit indicator status (ON/OFF) or (1/0)

when a transit vehicle is expected to reach/not to

reach the queue to be served by the phase.

The above measures are utilized with other fixed

indicators for each phase (such as link length and

number of lanes) to estimate the so-called green

weight for each phase, which is subsequently used in

estimating the green splits for all the intersection

traffic signal phases.

The devised fuzzy controller is assessed using a

mesoscopic simulation model (developed as a Visual

Basic Application VBA embedded EXCEL macro),

which can be then easily integrated with any fuzzy

logic controller. The FLM is integrated with the

simulation model via a two-way communication

protocol coded as a wrapper module macro in

EXCEL. The DLL representing the FLM is linked to

the simulator and receives inputs on the traffic

measures (representing the field detectors data). The

DLL estimates the traffic signal phase green splits

for the next time interval, etc. The estimated green

splits are then used by the simulator to simulate the

next time cycle. The calibration of the FLM is done

via systematic sensitivity analysis as will be

discussed later.

3 SIGNAL CONTROL FUZZY

LOGIC STRUCTURE

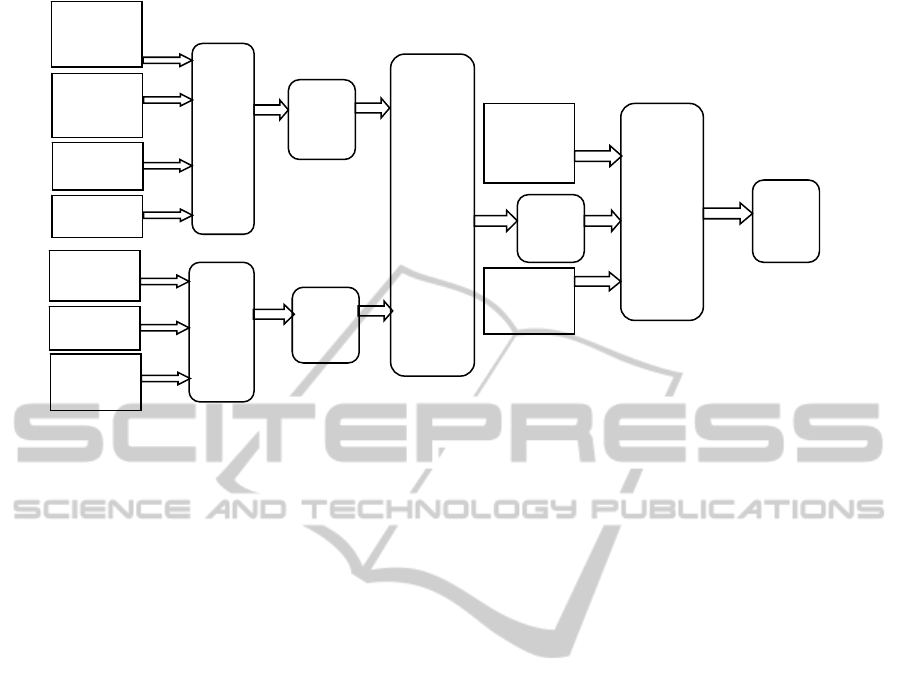
Figure 1 shows the fuzzy system structure including

input variables, rule blocks and output variables. The

connecting lines symbolize the data flow among the

various rule blocks. As shown, the system comprises

four rule blocks denoted by RB1, RB2, RB3 and

RB4. The first rule block (RB1) has four inputs; the

incoming approach’s average speed (km/hr), the

vehicular flow (veh/hr/lane), the length (m), and the

number of lanes. The second rule block (RB2) has

three input variables; traffic count on approach

(pcu), queue count on approach (pcu), and the truck

percentage. The time varying input variables are

calculated using the traffic status estimators (Hawas,

2010). The third rule block (RB3) has two

intermediate inputs; the output variables of the first

and second rule blocks. These are denoted by the

green weight I and II. The output of the third rule

block is denoted by the total green weight, which

represents the sum of these input variables (green

weight I and green weight II).

The fourth rule block (RB4) has three inputs; the

total green weight (the output of the third rule

block), the downstream blockage index, and the

transit vehicle indicator (a binary variable: 1 if a

transit vehicle is to be served during the current

cycle and 0 otherwise). The overall system output is

denoted by the “final weight” and it represents the

estimated weight given to the traffic light phase that

serves the approach under consideration.

The two rule blocks RB1 and RB2 complete each

other in estimating the green weight. With reference

to Figure 2, RB3 acts as “addition” rule block

(adding the initial weights estimated by the RB1 and

RB2). The result of such addition (output of RB3) is

then combined with the effect of the downstream

blockage [if activated] and the transit vehicle pre-

emption [if activated] in RB4. The multiple rule

block structure of the FLM is widely recommended

in literature as it simplifies the sensitivity analysis,

the calibration process of the fuzzy memberships,

and the identification of the most significant

contributing factors.

The results of the fuzzy-logic inference process

are linguistic terms describing the output variable

(e.g. Low Final-Weight, Medium Final-Weight, etc).

Each linguistic term covers a specific range of

numerical values. The defuzzification process is

responsible for converting the linguistic terms to

numerical crisp values (of this particular range).

The crisp value obtained by the defuzzification

process represents the system’s estimate of the

approach (phase) green weight. The weight is a real

number representing the “importance” of serving

this particular traffic light phase; the higher the

weight, the more the green to assign to this phase.

The green split,



of any phase



and

intersection i is estimated using a proportion formula

that entails the weight of the phase,

as follows:









(1)

Where:



: Actual green time of phase



at intersection i



: Total number of phases

: Total actual green time at intersection i



: Estimated weight by the FLM for phase



4 EXPERIMENTAL ANALYSES

AND RESULTS

To assess the effectiveness of the FLM, several

A FUZZY LOGIC MODEL FOR NETWORK SIGNAL CONTROL AND TRANSIT PREEMPTION

453



Average

Approach

Speed

Approach

Vehicular

Flow

Approach

Length

Numberof

Lanes

TrafficCount

onApproach

QueueCount

onA

roach

Truck

Percentage

Transit

Vehicle

Preemption

Downstream

Link

Congestion

Index



RB1



RB4



RB3



RB2

Green

Weight

I

Green

Weight

II

Total

Green

Weight

Final

Green

Weight

Figure1: Traffic signal control FLM structure, and rule blocks.

simulation-based scenarios were developed. A

single four-leg intersection is tested with different

traffic and geometric characteristics representing the

different scenarios. Different approach variables

were used to introduce variability in approach flow,

length, number of lanes, free-flow speed, and truck

percentages. Each approach is assumed to be served

by a separate phase. Herein, we provide only a

sample of these scenarios as well as their results.

Each scenario is tested using a duration time of 1800

seconds to generate vehicles and 2000 seconds to

clear the network. All scenarios were also tested

using a fixed cycle time of 100 seconds.

The minimum number of phases to serve a four-

leg intersection varies based on the traffic volumes

and type of the left turning phases (protected,

permitted). For instance, if a four-leg intersection is

to be served with the left turning volumes permitted,

then a two-phase cycle would be needed. A four-

phase signal would be needed if left turning volumes

are to be served in a protected mode. In this paper, a

4-phase signal setting was used for simplicity, and to

account for the fact that any potential left turning

vehicles along the approach would have to be served

in a protected mode.

The FLM applies to any number of phases and

signal configuration (e.g. two, three, four phase

signals). For instance, for a 4-leg two-phase signal

(combining the through movements on opposing

approaches), the FLM runs similarly on all four

approaches; estimating a green weight for each.

Then, the critical approach (of each phase) is

identified as the one having higher green weight. In

the implementation of the green splits, the critical

approach green weight would be considered in

estimating the phase green times. The green time of

any phase (combining various movements) is

determined in accordance to the most critical

movement served by the phase. The logic allows for

phase skipping if the phase’s green weight is lesser

than a pre-specified threshold value (if warranted). If

a phase is skipped, the following phase in the (fixed)

sequence is activated.

The inference engine of the 4

rule block was

developed using sensitivity analysis. Initially, a

correlation coefficient of 1.0 was assumed between

the total green weight and the final green weight, a

negative correlation (of -1.0) between the

downstream congestion index and the final green

weight, and a positive correlation of (1.0) between

the final green weight and the transit vehicle

preemption. The four experimental scenarios (in

Table 1) were run and the average vehicle travel and

delay times were estimated. The correlation

coefficients were then slightly adjusted and again the

average travel and delay times were estimated. The

process of readjusting the correlation coefficients

and the estimation of the travel and delay times were

repeated until the system converges to minimal

travel and delay times. The correlation coefficients

corresponding to the minimal travel and delay times

are 0.9, -0.8 and 0.75 for the total green weight, the

downstream congestion index and the transit vehicle

preemption, respectively.

The “base” Scenario (I) represents a medium

congested network, assumes no downstream

congestion and no transit preemption. The other

three scenarios are similar to scenario I (in terms of

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

454

the speed, the vehicular flow, the link length, the

number of lanes and the truck percentage), but they

differ in the downstream congestion values and/or

the transit preemption.

Several other scenarios were previously tested

and reported in Hawas (2010) using the isolated

signal FLM. The reported scenarios accounted only

for variations in the input variables of RB1 and RB2.

They also accounted for scenarios with and without

“knowledge estimator” activated. No consideration

was given in Hawas (2010) to the downstream

congestion effect or to the transit vehicle preemption

influence [the inputs to RB4]. This paper extends on

the work presented earlier in Hawas (2010) by

accounting for the downstream congestion and the

transit preemption.

The analysis presented in this paper focuses on

illustrating how the resulting FLM green times are

influenced by the downstream congestion index and

the transit vehicle preemption variables. That is,

how will the green times patterns correspond to

various patterns of network congestion and transit

preemption scenarios.

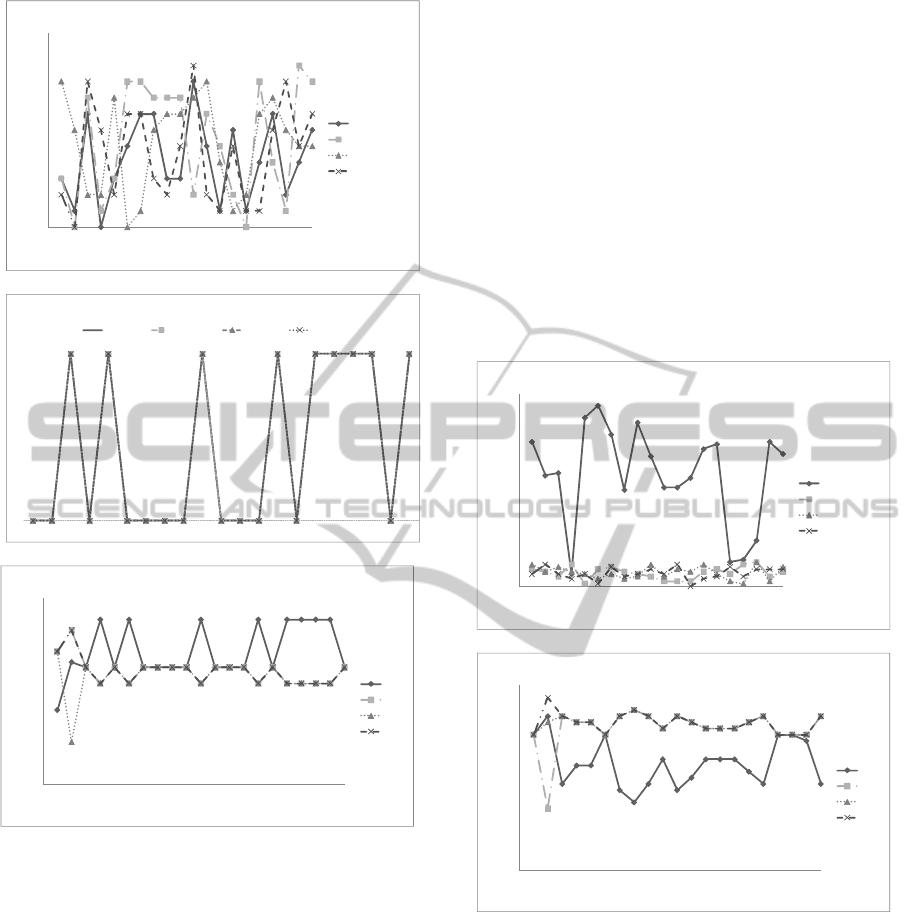
Figure 2 illustrates the results of scenario I.

Figures 2A and 2B shows the estimated queue

length and the traffic count on each approach

(estimated by the knowledge estimator). Because of

the identical traffic conditions on all approaches

(speed, traffic volume, link length, number of lanes,

truck percentage), the approaches exhibit similar

queue length and traffic count patterns. The resulting

green times (of the FLM) are equal among the

various phases as shown in Figure 2C.

Table 1: Basic information of different tested scenarios.

Scenario*

Downstream congestion

index

Transit vehicle pre-

emption

10% or less on

downstream links of all

approaches

No transit preemption

10% or less on

downstream links of all

approaches

Transit preemption on

NB approach only

III

80% or less on

downstream link of NB

approach

No transit preemption

80% or less on

downstream link of NB

approach

Transit pre-emption

on NB approach only

*All scenarios are set equal in link speed, link length, number of

lanes, link vehicular flow, and truck percentage (60 km/hr speed,

500 veh/hr/lane vehicular flow, 500 m length, 2 lanes and 10%

trucks).

00000000000

0000

00000

1234567891011121314151617181920

QueueLength(PCU)

Cycle

QueueLength

North

West

South

East

(2A) Approach queue length (in PCU).

10 10

1234567891011121314151617181920

ApproachVolumeCount(PCU/Lane)

Cycle

ApproachVolumeCount

North

West

South

East

(2B) Approach volume count (PCU/lane).

22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 2222

22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22 22

12345678910111213141516171819202122

PhaseGreenTime(sec)

Cycle

PhaseGreenTimes

North

West

South

East

(2C) Phase green times (sec).

Figure 2: Results of experimental scenario I.

Scenario II is quite similar to scenario I. Slight

congestion is exhibited on the downstream

approaches (a congestion index of 10% or less) as

shown in Figure 3A. The only difference (between

the two scenarios) is that the transit vehicles

incoming on the North bound (NB) approach are

pre-empted (in scenario II). Figure 3B illustrates the

cycles during which transit vehicles arrive at the

intersection. The resulting FLM signal green times

(in Figure 3C) are somehow identical for all the

approaches except the NB. The resulting green time

pattern of the NB approach (in Figure 3C) is

consistent with the transit vehicle arrival pattern

(Figure3B).

A FUZZY LOGIC MODEL FOR NETWORK SIGNAL CONTROL AND TRANSIT PREEMPTION

455

888

123456789101112131415161718192021

DownstreamBlockageIndex

Cycle

DownstreamCongestion

Dn_Str‐Cong_N

Dn_Str‐Cong_W

Dn_Str‐Cong_S

Dn_Str‐Cong_E

(3A) Downstream approach congestion index.

0000

000

1111

0000

000

0000

000

0000

000

0000

123456789101112131415161718192021

Transit

Transit_N Transit_W Transit_S Tra nsit_E

(3B) Transit vehicles arrival pattern.

22 22 22 22

22 22 22

31 31 31 31

22 22 22 22

22 22 22

19 19 19 19

22 22 22 22

22 22 22

19 19 19 19

22 22 22 22

22 22 22

19 19 19 19

12345678910111213141516171819202122

PhaseGreenTime(sec)

Cycle

PhaseGreenTimes

North

West

South

East

(3C) Phase green times (sec).

Figure 3: Results of experimental scenario II.

Scenario II represents the case of the FLM

control system that is not only reactive to the traffic

conditions along the incoming approaches, but also

reactive to the incoming transit vehicles. Currently,

all transit vehicles are pre-empted equally. That is,

the FLM operates with a binary variable that

activates the system’s transit pre-emption logic,

without providing any preferential treatment to

various transit vehicles. The FLM shall be extended

in further research to provide various levels of pre-

emption based on the vehicle type, the transit

vehicle’s passenger occupancy and the distance

between the transit vehicle and the approach’s stop-

line.

Scenario III is developed by introducing slight

variations to scenario I. Similar to scenario I, slight

congestion is exhibited on the downstream

approaches of the intersection (a congestion index of

10% or less) as shown in Figure 3A. Only the

downstream of the NB approach exhibits oscillating

congestion (congestion index of 80% or less) as

shown in Figure 4A. The transit pre-emption is

activated. The resulting FLM signal green times (in

Figure 4B) of the NB approach is lesser than that of

the other approaches (although the traffic conditions

are identical). The FLM (due to the congestion

downstream the NB approach) allocates lesser green

times to the NB phase. The higher the congestion

index, the lesser the green times.

41 41

222

777

123456789101112131415161718192021

Downstream BlockageIndex

Cycle

DownstreamCongestion

Dn_Str‐Cong_N

Dn_Str‐Cong_W

Dn_Str‐Cong_S

Dn_Str‐Cong_E

(4A) Downstream approach congestion index.

17 17

18 18 18

22 22

24 24

23 23 23

22 22 22

24 24

23 23 23

22 22 22

24 24

23 23 23

22 22 22

12345678910111213141516171819202122

PhaseGreenTime(sec)

Cycle

PhaseGreenTimes

North

West

South

East

(4B) Phase green times (sec).

Figure 4: Results of experimental scenario III.

Scenario IV combines the congestion

downstream the NB approach (Figure 5A) and the

transit preemption on the NB approach (Figure 5B).

The resulting NB green times as such oscillates to

balance the two conflicting criteria; lesser green time

due to the downstream congestion and the higher

green time due to the transit preemption. The

resulting green times of the various intersection

phases is illustrated in Figure 5C.

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

456

333

123456789101112131415161718192021

DownstreamBlockageIndex

Cycle

DownstreamCongestion

Dn_Str‐Cong_N

Dn_Str‐Cong_W

Dn_Str‐Cong_S

Dn_Str‐Cong_E

(5A) Downstream approach congestion index.

000

1111

111

0000

000

0000

000

0000

000

123456789101112131415161718192021

Transit

Tra nsit_N Tra nsit_W Transit_S Transit_E

(5B) Transit vehicles arrival pattern.

26 26

2525

19 19

20 20

21 21

19 19

20 20

21 21

19 19

20 20

21 21

12345678910111213141516171819202122

PhaseGreenTime(sec)

Cycle

PhaseGreenTimes

North

West

South

East

(5C) Phase green times (sec).

Figure 5: Results of experimental scenario IV.

5 CONCLUSIONS AND FUTURE

RESEARCH

This paper presented a FLM that can be coupled

with smart “processing” tools to estimate several

traffic measures from multiple detectors on each

approach. The estimates obtained from this

processing tool are integrated as inputs into the

FLM. The FLM explicitly accounts for the

congestion on the links downstream the controlled

intersection. As such, the FLM can be regarded as a

semi-network control procedure. The FLM can also

adjust the signal settings to provide transit

preemptions. The presented FLM was tested with

four scenarios to assess the sensitivity of the model

to the downstream and the transit preemption

variables.

The resulting green time patterns clearly

illustrate the sensitivity of the FLM to the

congestion and the transit preemption variables.

More research is being undertaken to demonstrate

the presented model effectiveness in real-life

conditions. Also, comparative analysis of the

presented FLM effectiveness vis-à-vis other real-

time signal controllers shall be considered for future

research.

Further appealing improvement to the system can

be achieved by further processing of the raw data to

have estimates of the expected approach delays. The

green splits can be then adjusted to explicitly assign

green weight based on expected delay estimates.

This will be considered for the future upgrades of

the FLM. More sophisticated knowledge can be

formed by considering more than two detectors, and

better accuracy can be sought through modifying the

detector locations.

The presented FLM control system is not only

reactive to the traffic conditions along the incoming

approaches, but also reactive to the incoming transit

vehicles and the downstream approaches congestion.

Currently, all transit vehicles are pre-empted

equally. That is, the FLM operates with a binary

variable that activates the system’s transit pre-

emption logic, without providing any preferential

treatment to various transit vehicles. The FLM shall

be extended in further research to provide various

levels of pre-emption based on the vehicle type, the

transit vehicle’s passenger occupancy and the

distance between the transit vehicle and the

approach’s stop-line.

The downstream congestion is modelled herein

through congestion index that quantifies the degree

of downstream link occupancy. Future research shall

include the coupling of the FLM with smart

processors that can utilize the downstream

approach’s detector readings to provide better

estimates of the downstream congestion status; the

distribution of the vehicles, and extent of queues

along the downstream links.

Moreover, the FLM shall be also restructured as

a multi-level control system for incident detection,

signal control and transit priority. These systems

however if deployed individually may result in

conflicting decisions and as such they need to be

integrated to insure consistency of decisions leading

to optimized traffic network performance. The

multi-level FLM is envisaged to comprise three

A FUZZY LOGIC MODEL FOR NETWORK SIGNAL CONTROL AND TRANSIT PREEMPTION

457

levels. The first level shall be responsible for

detecting incidents in urban networks using field

street detectors. The second level shall operate a

heuristic based logic for real-time signal control with

extended capabilities to operate special scenarios if

incidents are detected, aiming at better traffic

management during such incidents. The third level

shall deploy several strategies for transit vehicles

priority. The three levels shall operate in a closed

loop fashion to insure consistency of decisions and

better traffic management. The system shall be

tested within a simulation-based environment under

various operational conditions reflecting network

congestion, incident situations, and transit demand

patterns.

REFERENCES

Bingham, E., 2001. “Reinforcement learning in neuro-

fuzzy traffic signal control”, European Journal of

Operational Research 131, pp. 232-241.

Chou C. and Teng, J., 2003. “A fuzzy logic controller for

traffic junction signals” Information Sciences 143. pp

73–97.

Hawas, Y. E., 2007. “A Fuzzy-Based System for Incident

Detection in Urban Street Networks” Transportation

Research Part C 15, pp 69–95.

Hawas, Y. E., 2010. “An integrated simulation-based

fuzzy logic model for real-time traffic signal control',

Transportmetrica,, First published on: 28 July 2010

(iFirst), pp 1-32 (URL: http://dx.doi.org/

10.1080/18128600903427645).

Henry, J. J., Farges, J. L. and Gallego, J. L., 1998. “Neuro-

fuzzy techniques for traffic control” Control

Engineering Practice 6, pp 755-761.

Kosonen, L., 2003. “Multi-agent fuzzy signal control

based on real-time simulation” Transportation

Research Part C 11, pp.389–403.

Mirchandani, P. and Head, L., 2001. “A real-time traffic

signal control system: architecture, algorithms and

analysis” Transportation Research Part C 9. pp 415-

432.

Murat, Y. S. and Gedizlioglu, E., 2005. “A fuzzy logic

multi-phased signal control model for isolated

junctions” Transportation Research Part C 13. pp.

19–36.

Niittymaki, J. and Pursula, M., 2000. “Signal control using

fuzzy logic”. Fuzzy Sets and Systems 116. pp 11-22.

Niittymaki, J. and Turunen, E., 2003. “Traffic signal

control on similarity logic reasoning” Fuzzy Sets and

Systems 133, pp. 109–131.

Palacharla, P. V. and Nelson, P. C., 1999. “Application of

fuzzy logic and neural networks for dynamic travel

time estimation” International Transactions in

Operational Research 6, pp 145-160.

Sugeno, M. and Nishida, M., 1985. “Fuzzy control to

model car”. Fuzzy Sets and Systems 16, pp. 103–113.

Traiba, M. B., Kaseko, M. S. and Ande, M., 1999. “A two-

stage fuzzy logic controller for traffic signals”

Transportation Research Part C 7, pp. 353-367.

Wen, W., 2007. “A dynamic and automatic traffic light

control expert system for solving the road congestion

problem” Experts Systems and Applications,

doi:10.1016/j.eswa.2007.03.007.

Zimmermann, H. J., 1996. Fuzzy Set Theory, Kluwer

Academic Publishers, Dordrecht. 1996.

FCTA 2011 - International Conference on Fuzzy Computation Theory and Applications

458