ENHANCING CLUSTERING NETWORK PLANNING

ALGORITHM IN THE PRESENCE OF OBSTACLES

Lamia Fattouh Ibrahim

Department of Computer Sciences and Information, Institute of Statistical Studies and Research

Cairo University, Cairo, Egypt

Currently Department of Information Technology, Faculty of Computing and Information Technology

King AbdulAziz University, B.P. 42808 Zip Code 21551- Girl Section, Jeddah, Saudi Arabia

Keywords: DBSCAN clustering algorithm, Network planning, Spatial clustering algorithm.

Abstract: Clustering in spatial data mining is to group similar objects based on their distance, connectivity, or their

relative density in space. In real word, there exist many physical obstacles such as rivers, lakes, highways

and mountains, and their presence may affect the result of clustering substantially. Today existing telephone

networks nearing saturation and demand for wire and wireless services continuing to grow,

telecommunication engineers are looking at technologies that will deliver sites and can satisfy the required

demand and grade of service constraints while achieving minimum possible costs. In this paper, we study

the problem of clustering in the presence of obstacles to solve network planning problem. In this paper,

COD-DBSCAN algorithm (Clustering with Obstructed Distance - Density-Based Spatial Clustering of

Applications with Noise) is developed in the spirit of DBSCAN clustering algorithms. We studied also the

problem determine the place of Multi Service Access Node (MSAN) due to the presence of obstacles in area

complained of the existence of many mountains such as in Saudi Arabia. This algorithm is Density-based

clustering algorithm using BSP-tree and Visibility Graph to calculate obstructed distance. Experimental

results and analysis indicate that the COD-DBSCAN algorithm is both efficient and effective.

1 INTRODUCTION

In network planning process, one of the difficult task

which are facing Telecommunication Company is

determining the best place and numbers of Multi

Service Access Node (MSAN).

The process of network planning is divided into

two sub problems: determining the location of the

switches or MSAN and determining the layout of the

subscribers' network lines paths from the switch to

the subscribers while satisfying both cost

optimization criteria and design constraints. Due to

the complexity of this process artificial intelligence

(AI) (Fahmy and Douligeris, 1997); (El-Dessouki et

al., 1999) partitioning clustering techniques (Fattouh,

et al., 2003); (Fattouh and Al Harbi, 2008a); (Al

Harbi and Fattouh, 2008); (Fattouh and Al Harbi,

2008b); (Fattouh, 2006); (Fattouh, 2005); (Fattouh et

al., 2005) has been successfully deployed in a

number of areas.

Clustering technique will be used for helping

engineers to improve the network planning by

determining the place of MSAN. Clustering is one of

the most useful tasks in data mining process. There

are many algorithms that deal with the problem of

clustering large number of objects. The different

algorithms can be classified regarding different

aspects. These methods can be categorized into

partitioning methods (Kaufman and Rousseeuw,

1990); (Han et al., 2001); (Bradly et al., 1998);

hierarchical methods (Kaufman and Rousseeuw,

1990); (Zhang et al., 1996); (Guha et al., 1998);

density based methods (Ester et al., 1996); (Ankerst

et al., 1999); (Hinneburg and Keim, 1998), grid

based (Wang et al., 1997); (Sheikholeslami et al.,

1998), (Agrawal et al., 1998) methods, and model

based methods (Shavlik and Dietterich, 1990);

(Kohonen, 1982). The clustering task consists of

separating a set of objects into different groups

according to some measures of goodness that differ

according to application. The application of

clustering in spatial databases presents important

characteristics. Spatial databases usually contain

very large numbers of points. Thus, algorithms for

480

Fattouh Ibrahim L..

ENHANCING CLUSTERING NETWORK PLANNING ALGORITHM IN THE PRESENCE OF OBSTACLES.

DOI: 10.5220/0003686304720478

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 472-478

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

clustering in spatial databases do not assume that the

entire database can be held in main memory.

Therefore, additionally to the good quality of

clustering, their scalability to the size of the database

is of the same importance (Nanopoulosl et al., 2001).

In spatial databases, objects are characterized by

their position in the Euclidean space and, naturally,

dissimilarity between two objects is defined by their

Euclidean distance (Yiu and Mamoulis, 2004).

In many real applications the use of direct

Euclidean distance has its weaknesses (Yiu and

Mamoulis, 2004). The Direct Euclidean distance

ignores the presence of streets, paths and obstacles

that must be taken into consideration during

clustering.

In this paper, a clustering–based solution is

presented depending on using the obstructed distance

and density-Based Clustering techniques.

DBSCAN is Density-Based (Tan et al., 2006)

algorithm which is used when a cluster is a dense

region of points, which is separated by low-density

regions, from other regions of high density. In this

paper we modify DBSCAN to achieve the helping

for engineers.

In section 2 the DBSCAN Clustering algorithm

are reviewed. In section 3, the

COD-DBSCAN

algorithm is introduced. A case study is presented in

section 4. Section 5 discusses related work. The

paper conclusion is presented in section 6.

2 DBSCAN ALGORITHM

DBSCAN is a density-based algorithm. Density is

the number of points within a specified radius (Eps).

DBSCAN defines three types of points. A point is a

core point if it has more than a specified number of

points (MinPts) within Eps. These are points that are

at the interior of a cluster (in the interior of density-

based cluster). A border point has fewer than MinPts

within Eps, but is in the neighborhood of a core

point. A noise point is any point that is not a core

point or a border point. Figure 1 shows the three

types of point. Figure 2 shows the original DBSCAN

clustering algorithm.

3 COD-DBSCAN ALGORITHM

The existing of the natural obstacle is affecting on

distribution the MSAN on the regions. The

responsible operator is looking to rapidly provide

thousands of new subscribers with high-quality

telephone service and provide the right equipment,

at the right place, and at the right time, with

reasonable cost in order to satisfy expected demand

and acceptable grade of service.

Figure 1: Type of points used in DBSCAN.

DBSCAN Algorithm

Ignore noise points

Perform clustering on the remaining

points

Current-cluster-label = 0

For all core points do

If the core point has no cluster

label then

Current-cluster-label=current-cluster-

label + 1

Label the current core point with cluster

label current-cluster-label

End if

For all points in the Eps-neighborhood,

except i

the point itself do

If the point does not have a cluster

label then

Label the point with cluster label

current-cluster-label

End if

End for

Figure 2: DBSCAN Clustering Algorithm.

In a certain city, contains number of subscribers,

we need to determine the number of MSAN

requirements and define their boundaries in such

away that satisfy good quality of service with

minimum cost.

The problem statement:

 Input: A set P data points {p

, p

… p

} in 2-D

map which represent intersection nodes, coordinates

of each node, a map of streets, distribution of the

subscribers’ loads within the city and the location of

obstacles in this city.

 The available cable sizes, the cost per unit for

each size and the maximum distance of wire that

ENHANCING CLUSTERING NETWORK PLANNING ALGORITHM IN THE PRESENCE OF OBSTACLES

481

satisfied the allowed grade of service.

 Objective: Partition the city into k clusters

, .., C

} that satisfy clustering constraints,

such that the cost function is minimized with high

grade of services.

 Output: k clusters, the location of MSAN, the

wire branching from each MSAN to subscriber and

boundaries of each cluster.

The proposed algorithm contains two phases. The

following sections describe these two phases.

3.1 Phase I : Pre-planning

The maps used for planning are scanned images

obtained by the user. It's need some preprocessing

operations before it used as digital maps, we draw

the streets and intersection nodes on the raster maps,

the beginning and ending of each street are

transformed into data nodes, defined by their

coordinates. The streets themselves are transformed

into links between data nodes. The subscriber’s

loads are considered to be the weights for each

street.

3.2 Phase II: Main-planning Phase

COD-DBSCAN is divided into two step:

1- Step 1: Preprocessing.

2- Step 2: Modified DBSCAN algorithm.

3.2.1 Preprocessing

During the course of clustering, the COD-DBSCAN

often needs to compute the obstructed distance

between a point and a temporary cluster center. Our

aim of pre-processing here is to manipulate

information which will facilitate such computation.

3.2.1.1 The BSP-tree

The Binary-Space-Partition (BSP) tree (Anthony et

al., 2001) is a data structure which can efficiently

determine whether two points p and q can visible to

each other within the region R. We define p to be

visible from q in the region R if the straight line

joining p and q does not intersect any obstacles. In

our algorithm, the BSP-tree is used to determine the

set of all visible obstacle vertices from a point p.

henceforth, we will use the notation vis(p) to denote

such a set of vertices.

3.2.1.2 The Visibility Graph

Given a set of m obstacles, O = {o

, o

,……o

}, the

visibility graph is a graph VG = (V, E) such that

vertex of the obstacles has a corresponding node in

V, and two nodes v

and v

in V are joined by an

edge in E if and only if the corresponding vertices

they represent are visible to each other. To generate

VG, we make use of the BSP-tree computed

previously and search all other visible vertices from

each vertex of the obstacles. The visibility graph is

pre-computed because it is useful for finding the

obstructed distance between any two points in the

region.

In Figure 3, we show the visibility graph VG' can

be derived from the visibility graph VG of a region

with two obstacles o

and

3.2.2 Modified DBSCAN Algorithm

Two parameters must be determine before we starts

applying the DBSCAN. These parameters are

MinPts and Eps. In network planning the cable

length must be at maximum 2.5 km for 0.4 cm

diameters to achieve an acceptable grade of service.

So, we make the value of EPS take the value of

shortest path from core (MSAN) to the most remote

point (subscribers) which is 2.5 km. The original

DBSCAN Algorithm uses Euclidian distance (that

means the direct distance between the MSAN and

nodes); The Direct Euclidean distance ignores the

presence of streets, paths and obstacles that must be

taken into consideration during clustering. In this

paper, a clustering –based solution is presented

depending on using the physical shortest obstacle

distance visibility graph algorithm.

Figure 3: A visibility graph.

When the congestion in MSAN is occur or the

number of subscribers is less than 100 we use

mobile tower as auxiliary tool to serve this small

number of subscribers. Therefore the value of

MinPts is set to 101.

The DBSCAN classes of nodes to:

- Core point which is a subset of candidate MSAN

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

482

location.

- Noise point: In real planning all subscribers must

be served so noise point is served using the mobile

tower which can serve at maximum 100 subscribers

because that number is the maximum subscriber who

can be served by mobile tower.

- Border point that belong to ascertain cluster.

Figure 4 shows pseudo code of COD-DBSCAN

algorithm used. The user first inserts the location of

candidate MSAN. Our package uses these candidate

locations as candidate core points and chooses the

one which satisfies the condition to be a core node.

After this step the package determine the boundaries

of cluster by calculate the obstacle distance from

node to each core by construct BSP tree and

visibility graph and allocate the node to the

minimum obstacle distance core.

Figure 4: Implementation of COD-DBSCAN algorithm.

4 CASE STUDY

For real application, the proposed algorithm is

applied on a map representing a district in Saudi

Arabia. The actual map is scanned. The beginning

and ending of each street are transformed into data

points, defined by their coordinates. The streets

themselves are transformed into linkages between

data points.

The COD-DBSCAN algorithm divided the map

into the convenient number of clusters in which the

load of subscribers is distributed.

Figure 5 shows this area if we used clustering

algorithm without considering the obstacles effect.

Figure 6 show the map after applying COD-

DBSCAN algorithm which divide the map into 6

clusters.

Figure 5: Clustering when ignore the present of obstruct.

Figure 6: Using COD-DBSCAN algorithm considering the

location of obstruct.

5 RELATED WORK

Table 1 compares related work. In Gravity Center

algorithm (El-Dessouki et al., 1999), the city is

divided into four quadrants at the center of gravity

which are the number of clusters. Checking the

network constraints for each quadrant, if the

constraints are satisfied, the number of clusters will

be four quadrants (clusters). The switches will be

located at the center of gravity of each cluster. If the

constraints are not satisfied in any of the four

quadrants the same partitioning method is applied to

the quadrant which does not satisfy the constraints.

This yields that the number of clusters equal seven

partitions. This method will be iterated until the

MSAN

ENHANCING CLUSTERING NETWORK PLANNING ALGORITHM IN THE PRESENCE OF OBSTACLES

483

network constraints are satisfied. The resulting

number of clusters may be 4, 7, 10, Etc. This work

doesn’t reflect the real nature of the clusters, or the

number of the suitable clusters, it is always

incrementing the number of clusters by three.

COD-CLARANS (Anthony et al., 2001) and

CSPw-CLARANS (Fattouh et al., 2003); (Khaled et

al., 2003) algorithms depend mainly on CLARANS

which is design to deal with large database by using

multiple different samples. These two algorithms is

very powerfully when we plan a large city, but not

acute when we plan small city due the sampling use.

Ant-Colony-Based Network Planning Algorithm

(Fattouh et al., 2005) used Gravity center to find the

location of switch and applied a modified version of

Ant-colony algorithm to find the shortest path. The

algorithm is very powerful when the network is

complicated and we have a large number of

intersection and streets. CWSP-PAM (Fattouh,

2005) algorithm depends mainly on PAM clustering

algorithm. This algorithm use Floyd-Warshall

algorithm to find short path.

CWSP-PAM-ANT (Fattouh, 2006) algorithm use

modifies clustering technique PAM and Ant-colony

algorithm to the network planning problem. This

algorithm using weighted shortest paths that satisfy

the network constraints and where the weights used

are the subscriber loads. Experimental results and

analysis indicate that the COD-DBSCAN algorithm

is effective to satisfied subscribers demand for

network construction in an area where small number

of subscribers is present in non density area due to

the use of mobile network taking into consideration

the presence of obstacles.

6 CONCLUSIONS

Clustering analysis is one of the major tasks in

various research areas. The clustering aims at

identifying and extracting significant groups in

underlying data. Based on certain clustering criteria

the data are grouped so that the data points in a

cluster are more similar to each other than points in

different clusters. In this paper, we introduced a

clustering solution to the problem of network

planning, the COD-DBSAN algorithm. This

algorithm used clustering algorithm which are

density-based clustering algorithm using distances

which are obstacle distance and satisfying the

network constraints. This algorithm uses wire and

wireless technology to serve the subscribers demand

and place the switches in a real place. Experimental

results and analysis indicate that the algorithm was

effective to satisfied subscribers demand for network

construction in an area where obstacles are present

and satisfy the grade of service constraints required.

Table 1: Comparison of related work.

Algorithm

Name

Algorithm

Type

Input

Parameters

Results Constraint Location of Exchange

Type of

Distance

Gravity

Center

Gravity

Center

Algorithm

Data Points

Divide a

block in

4,7,10…

block

Yes,

network

constraints

At the gravity center

= number of subscribers in locati

coordinates X

Shortest path

distance

Floyd-

Warshall

algorithm

COD-

CLARANS

partitioning

method

Data points

Number of

clusters (k)

Maximum

number of

neighbors

Medoids

clusters

Yes,

obstacles

constraints

At the medoids

Obstructed

distance

CSPw-

CLARANS

partitioning

method

Data points

Medoids

clusters

Yes,

network

constraints

At medoids with min

Where c

is the medoids of C

d″(c

, p

) is the shortest path from p

to c

, L

is the load cost of this

shortest

Shortest path

Distance

Floyd-

Warshall

algorithm

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

484

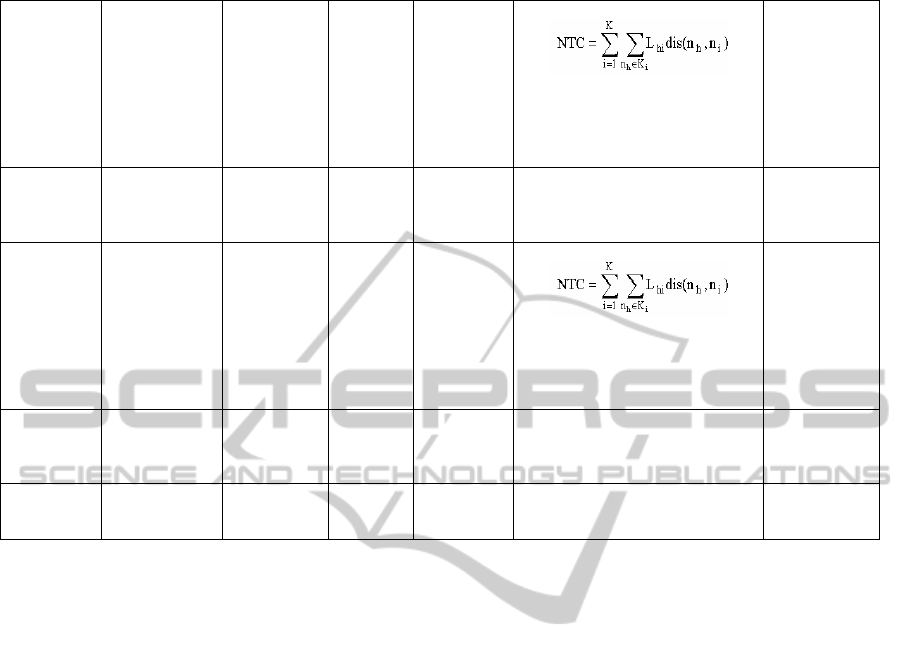
Table 1: Comparison of related work (cont.).

CWSP-

PAM

partitioning

method

Data points

Medoids

clusters

Yes,

network

constraints

At medoids with min

Where n

is the medoids of cluster

, dis(n

, n

) is the shortest path

from n

to n

, L

is the subscribers

load

cost of this shortest path

Shortest path

Distance

Floyd-

Warshall

algorithm

Ant-Colony-

Based

Network

Planning

Gravity

Center

Algorithm

Data points

Divide a

block in

4,7,10…

block

Yes,

network

constraints

At the gravity center

Shortest path

distance Ant-

Colony

CWSP-

PAM-ANT

partitioning

method

Data points

Medoids

clusters

Yes,

network

constraints

At medoids with min

Where n

is the medoids of cluster

, dis(n

, n

) is the shortest path

from n

to n

, L

is the subscribers

load

cost of this shortest path

Shortest path

Distance Ant-

Colony

Algorithm

NetPlan

Density-based

agglomerative

clustering

- Data points

- Candidate

switch

Location

- Core of

the

cluster

Yes,

network

constraints

At core of the cluster

Shortest path

distance

Dijkstra

algorithm

COD-

DBSCAN

Density-based

Visibility graph

Data points

Core of

the

cluster

Yes,

network

constraints

At core of the cluster The BSP-Tree

REFERENCES

Agrawal, R., Gehrke, J., Gunopulos, D., Raghavan,P.,

(1998). Automatic subspace clustering of high

dimensional data for data mining application. In Proc.

1998 ACM-SIGMOD Int. Conf. Management of Data

(SIGMOD’98).

Ankerst, M., Breunig, M., kriegel, H. and Sander, J.,

(1999). OPTICS: Ordering points to identify the

clustering structure. In Proc. 1999 ACM-SIGMOD Int.

Conf. Management of data ( SIGMOD’96).

Anthony K., Tung, H. Hou, H. and Han, J., (2001). Spatial

Clustering in the presence of obstacles. Proc. 2001 Int.

Conf. on Data Engineering (ICDE'0).

Bradly, P., Fayyad, U. and Reina, C., (1998). Scaling

clustering algorithms to large databases. In proc. 1998

Int. Conf. Knoweldge Discovery and Data mining.

El Harby, M., Fattouh, L., (2008). Employing of

Clustering Algorithm CWN-PAM in Mobile Network

Planning. The Third International Conference on

Systems and Networks Communications, ICSNC 2008,

Sliema, Malta, October 26-31.

El-Dessouki, A., Wahdan, A., Fattouh, L., (1999). The

Use of Knowledge-based System for Urban Telephone

Planning. International Telecommunication Union,

ITU/ITC/LAS Regional Seminar on Tele-Traffic

Engineering for Arab States, Damascus, Nov. 7-12.

Ester, M., Kriegel, H., Sander, J. and Xu, X., (1996). A

density based algorithm for discovering clusters in

large spatial databases. In Proc. 1996 Inc. Conf.

Knowledge discovery and Data mining (KDD’96).

Fahmy, H. And Douligeris, C. (1997). Application Of

NeuralNetworks And Machine Learning In Network

Design. IEEE Journal In Selected Areas In

Communications, Vol. 15, No. 2, Feb.

Fattouh, L. (2006). Using of Clustering and Ant-Colony

Algorithms CWSP-PAM-ANT in Network Planning.

International Conference on Digital

Telecommunications (ICDT 2006), Cap Esterel,

French Riviera, France, 26-31 August.

Fattouh, L., Al Harbi, M., (2008a). Employing Clustering

Techniques in Mobile Network Planning. Second IFIP

International Conference on New Technologies,

Mobility and Security, Tangier, Morocco, 5-7

November.

Fattouh, L., Al Harbi, M., (2008b). Using Clustering

Technique M-PAM in Mobile Network Planning. The

12th WSEAS International Conference on

COMPUTERS, Heraklion, Crete Island, Greece, July

23-25.

Fattouh, L., (2005). Using of Clustering Algorithm

CWSP-PAM for Rural Network Planning. 3rd

International Conference on Information Technology

and Applications, ICITA'2005, Sydney, Australia, July

4-7.

Fattouh, L., Metwaly, O., Kabil, A., Abid, A., (2005).

Enhancing the Behavior of the Ant Algorithms to

Solve Network Planning Problem. Third ACIS

ENHANCING CLUSTERING NETWORK PLANNING ALGORITHM IN THE PRESENCE OF OBSTACLES

485

International Conference on Software Engineering,

Research, Management and Applications (SERA

2005), Mt. Pleasant, Michigan, USA, 11-13 August.

Fattouh,L., Karam, O., El Sharkawy, M., Khaled, W.,

(2003). Clustering For Network Planning. WSEAS

Transactions on Computers, Issue 1, Volume 2,

January.

Guha, S., Rastogi, R., and Shim, K. (1998). Cure: An

efficient clustering algorithm for large databases. In

Proc. 1998 ACM-SIGMOD Int. Conf. Management of

Data (SIGMOD’98).

Han, J., Kamber, M., and Tung, A., (2001). Spatial

Clustering Methods in data mining: A Survey,

Geographic Data Mining and Knowledge Discovery.

Hinneburg, A. and Keim, A., (1998). An efficient

approach to clustering in large multimedia databases

with noise. In Proc. 1998 Int. Conf. Knowledge

discovery and Data mining (KDD’98).

Kaufman L., and Rousseeuw, P., (1990). Finding groups

in Data: an Introduction to cluster, John Wiley & Sons.

Khaled, W., Karam, O., Fattouh, L., El Sharkawy, M.,

(2003).CSPw-CLARANS: an Enhanced Clustering

Technique for Network Planning Using Minimum

Spanning Trees. International Arab Conference on

Information Technology ACIT’2003, Alexandri,

Egypt, December 20-23.

Kohonen, T.,(1982). Self organized formation of

topologically correct feature map. Biological

Cybernetics.

Nanopoulos, A., Theodoridis, Y., Manolopoulos, Y.,

(2001). C2P: Clustering based on Closest Pairs.

Proceedings of the 27th International Conference on

Very Large Data Bases, p.331-340, September 11-14.

Sheikholeslami, G., Chatterjee, S. and Zhang, A., (1998).

Wave Cluster: A multi- resolution clustering approach

for very large spatial databases. In Proc. 1997 Int.

Conf. Very Large Data Bases (VLDB’97).

Tan, P., Steinback, M., and Kumar, V., (2006).

Introduction to Data Mining. Addison Wesley.

Wang, W., Yang, J., and Muntz, R., (1997). STING: A

statistical information grid approach to spatial data

mining. In Proc. 1997 Int. Conf. Very Large Data

Bases (VLDB’97).

Yiu, M., Mamoulis, N. (2004). Clustering Objects on a

Spatial Network. SIGMOD Conference p 443-454.

Zhang, T., Ramakrishnan, R., and Livny, M., (1996).

BIRCH: an efficient data clustering method for very

large databases. In Proc. 1996 ACM-SIGMOD Int.

Conf. Management of data (SIGMOD’96).

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

486