
KNOWPATS: PATTERNS OF DECLARATIVE KNOWLEDGE
Searching Frequent Knowledge Patterns about Object-orientation
Peter Hubwieser and Andreas Mühling
Technische Universität München, Fakultät für Informatik, Boltzmannstr. 3, 85748 Garching, Germany
Keywords: Knowledge patterns, Knowledge mining, Concept maps, Declarative knowledge, Computer science
education.
Abstract: In order to better understand the structure of students’ knowledge in computer science, we are trying to
identify patterns – in form of frequently occurring subgraphs – in concept maps. Concept maps are an exter-
nalization of a person’s declarative knowledge represented as a graph. We propose an algorithm that can be
employed to identify frequently occurring subgraphs, based on existing algorithms in that field. We are cur-
rently working on a project that will gather concept maps form a large group of freshman in the coming
semesters, providing us with extensive material for information mining about the structures of knowledge in
CS. We hope to get a better understanding of the relationship between knowledge and competence.
1 INTRODUCTION
During the last decades, the focus of educational
research activities has shifted from knowledge to
competencies. This makes sense, because at the end
of the learning process the students should be able to
do something instead of just to talk about it. Never-
theless, it might still be helpful to have an idea of the
knowledge that is needed to gain a certain compe-
tency. Nearly every teacher has already heard a
student sigh: “If I had known this before!” after
having solved a problem finally. Particularly, if
learning environments are designed following mod-
ern constructivist approaches, the students should be
active and should try to find solutions on their own.
If the teacher has a very detailed idea of what the
students need to know, he or she is able to support
the learning process with short, precise information
input.
Therefore, our long-term goal is to identify the
prerequisite knowledge for certain competencies. As
subject domain we chose the field of object-oriented
modeling and programming, because it is central to
Informatics in schools as well as in universities.
The first step was to find and evaluate suitable
methods for the investigation of student knowledge.
To this purpose we have investigated the structure of
the knowledge that was presented during a typical
non-major CS1 course (for students of engineering)
by extracting the relevant information out of the
teaching material (textbook and slides) and by ask-
ing the students to draw concept maps at different
points in time during the course. That way, we tried
to find out how the presented knowledge was taken
up and later externalized by the students. Additional-
ly, we are collecting concept maps about object
oriented programming from high school teachers
and students as well as from bachelor and teacher
students of Informatics at our university.
Our next goal is to identify typical knowledge
patterns (which we call knowpats) in the student
maps that might have been similarly presented in the
lectures. As our next step we want to find out how
the knowpats as expressed by the students correlate
with the type and duration of Informatics courses
they had attended at school. Finally, we aim to cor-
relate these patterns with certain competencies.
2 BACKGROUND
First of all we have to limit the range of knowledge
that might be relevant to our research. For this pur-
pose we rely on the categorization of (Anderson
2009), because it was designed for a similar purpose,
namely the assessment of learning objectives. They
distinguish between:
1. Factual Knowledge: “basic elements that stu-
dents must know to be acquainted with a discip-
line or solve a problem in it”,
358
Hubwieser P. and Mühling A..
KNOWPATS: PATTERNS OF DECLARATIVE KNOWLEDGE - Searching Frequent Knowledge Patterns about Object-orientation.
DOI: 10.5220/0003689203500356
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2011), pages 350-356
ISBN: 978-989-8425-79-9
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

2. Conceptual Knowledge: “the interrelationships
among the basic elements within a larger struc-
ture that enable them to function together,”
3. Procedural Knowledge: “how to do something:
methods of inquiry, and criteria for using skills,
algorithms, techniques and methods,”
4. Metacognitive Knowledge: “knowledge of cog-
nition in general as well as awareness of one’s
own cognition.”
A comparison of the definitions (see e.g. Ander-
son 2009; Anderson, 2005) shows that factual know-
ledge can be represented by propositions, Concep-
tual knowledge by propositional networks, semantic
networks or schemata. Procedural knowledge might
be described by scripts following (Schank and Abel-
son, 1977), while Metacognitive knowledge might
be hard to describe anyway.
The first two categories describe both declarative
knowledge, but we are interested mainly in the
second category, which comprises “’mental models’,
‘schemas’ or ‘theories’ that individuals may use to
help them organize a body of information in an in-
terconnected, non-arbitrary and systematic manner”
(Anderson, 2009).
There are many research activities that use con-
cept mapping techniques in order to investigate
cognitive structures, for example (Vanides et al.,
2005). The students are asked to draw a graph with
nodes representing concepts and with edges symbo-
lizing associations between these concepts, e.g. “is
a”. There are many measures for the assessment of
concept maps and many validations for these meas-
ures, e.g. (Shavelson and Ruiz-Primo, 1999), (Albert
and Steiner, 2005). (Sanders et al., 2008) compared
the knowledge of students in several nations using
concept mapping techniques. (Goldsmith and Da-
venport, 1990) developed a graph-theoretical meas-
ure for the similarity of graphs based on neighbor-
hood structures. (McClure et al., 1999) validated this
measure by correlating it with several scoring tech-
niques. Hereby, they also detected that the scoring of
locally correct edges using a master map is the most
convincing scoring technique for concept maps.
Nevertheless, we have to remember that a con-
cept map does not represent the knowledge of its
author directly, but has to be regarded merely as an
externalization of this knowledge that might be in-
fluenced by motivation, by the focus of attention or
by many other external influences (Norman, 1983).
Concerning the representation of the specific
subject domain knowledge of object-oriented pro-
gramming, (Pedroni and Meyer, 2010) proposed to
organize it in Trucs, (testable, re-usable units of
cognition) which are collections “of concepts, opera-
tional skills and assessment criteria”.
Usually the students start drawing concept maps
with a list of given concepts that they have to pick
nodes from and connect them by associations (Sand-
ers et al. 2008). Suitable concepts that could be in-
cluded in such a list might be taken from the “the
quarks of object-oriented development” that were
identified by (Armstrong, 2006), comparing several
definitions of “object-orientation”.
(Mons et al. 2008) introduced knowlets as small
knowledge elements, which are restricted to the
connection of two concepts. In regard of constructiv-
ist learning approaches we need larger graph struc-
tures, as (Kinchin et al., 2000) argues.
For the mining of frequent patterns in large
graphs (Inokuchi et al., 2000) proposed the Apriori-
based Algorithm AcGM. It uses the monotony of the
support of induced subgraphs.
= (
,
) is an
induced subgraph of = (,) if and only if
⊂ and ∀
,
∈
:
(
,
)
∈
⇔
(
,
)
∈
. The definition of the support of
is
(
)=
,
(1)
with
being the number of graph transactions
where
⊂ and being the total number of graph
transactions of . A transaction in our context is just
a graph. If
is an induced subgraph of
, the
monotony can be expressed as
(
)
≤
(
)
(2)
This allows to derive candidates for frequent sub-
graphs of size from already found frequent sub-
graphs of size −1.
(Dominguez, 2010) applied a clustering ap-
proach to Mining for hints in eLearning. They used
the K-Means clustering algorithm to group the stu-
dents according their abilities according to their
answers on 25 questions. Following this, association
rules and numerical analysis were applied to find
common patterns affecting the learners’ performance
that could be used use to provide hints to the stu-
dents of the following years.
(Madhyastha and Hunt, 2009) presented a me-
thod for mining multiple-choice assessment data for
similarity of the concepts that were represented by
the multiple choice responses. They used the result-
ing similarity matrix to visualize the distance and
hereby the relative difficulty of concepts among the
students in the class.
(Romero et al., 2010) explored the extraction of
rare association rules, gathering student usage data
from a Moodle system. They defined rare associa-
KNOWPATS: PATTERNS OF DECLARATIVE KNOWLEDGE - Searching Frequent Knowledge Patterns about
Object-orientation
359

tion rules are those that only appear infrequently
there even though they might be highly associated
with very specific data. Thus, these rules are sup-
posed to be appropriate for using with educational
datasets since they are usually imbalanced. To this
purpose they compared several frequent and rare
association rule mining algorithms, e.g. the A priori-
Frequent algorithm.
3 DECLARATIVE KNOWLEDGE
For our investigation we chose one of our currently
running courses, introducing freshmen of engineer-
ing into the fundamentals of object-oriented pro-
gramming (CS1 for non-majors). The course was
attended by about 40 students and taught in German
language, thus all the text material, the concepts and
the concept maps had to be translated from German
to English for this paper.
In order to compare the knowledge that was ex-
ternalized by the students with the knowledge they
should acquire by studying the course material, we
tried to find representations of the relevant informa-
tion that are as formal as possible. For that purpose
we have summarized all learning elements that we
expect the students to know by reducing the slides
and the textbook for the course (Hubwieser et al.,
2008) to a list of “naked” statements without any
examples or explanations (called knowledge ele-
ments), for example:
The state of an object is determined by the
values of its attributes.
(*)
In order to derive a list of concepts that should
form the possible nodes of the concept maps, we
reduced these statements in the following steps:
At first we listed all words that were contained in
the texts, sorted this list alphabetically (case-
sensitive) and removed all words starting with a
lower case letter. In German, this condition assures
that the deleted words are all non-nouns. We re-
moved all remaining non-nouns, transformed all
words to singular nominative and removed all varia-
tions or abbreviations of the same noun. Finally, all
proper nouns and all purely didactical, organization-
al and pedagogical keywords were omitted. After-
wards, we coded and categorized the resulting set of
words following the rules of qualitative research
(Mayring, 2000), finally obtaining a list of 40 con-
cepts (CL), e.g. aggregation, algorithm, association,
attribute, class, condition, conditional statemen.
We asked the students to draw their maps in the
following way: We presented the concepts of CL in
the form of a checklist. At first the students should
check all the concepts that they believed to know
something about. Following this, they should draw a
graph, using the checked concepts as nodes and
connecting these by associations, which all should
be denoted by suitable labels. For the evaluation of
the maps we have removed all associations that were
not labeled, assuming that these did not reflect any
precise knowledge.
To get an “expert map” that is as objective as
possible, we derived it from the same material that
we have used for the derivation of our CL. We
coded all sentences from the list of the knowledge
elements (see above) by the occurrence of one or
more of the 40 concepts of CL. Afterwards we pro-
duced a list of all sentences that were marked with
two or more concepts of CL, assuming that these
sentences might suggest associations between those
concepts. For the structure of our knowpats, we were
interested in the assumed arity of the associations
(see table 1) that were suggested by the 161 sen-
tences that contained more than one concept.
Table 1: Assumed arity of suggested associations.
Number
of concepts
Number
of sentences
Percentage
2 101
62,7%
3 40
24,8%
4 17
10,6%
5 3
1,9%
Following this, we translated the information
that was contained in these sentences to associations
by qualitative means, which ended up with a set of
98 associations that formed our objective expert map
and that was used e.g. to score the students’ maps by
comparing the names they gave to their associations
with the respective names in the expert map.
4 DATA GATHERING
Over the academic year 2010/11 we have gathered a
variety of concept maps from students of different
groups.
As described in Detail in (Hubwieser and
Mühling, 2011) we have collected four generations
of concept maps from the students of the CS1 course
at four distinct points in time. As the drawing was
done partly in the main lecture and partly in the
tutorials, we had varying numbers of participants.
The pre-test was done by 39 students before the
course started. The first mid-test was done by 38
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
360
students after 4 weeks. Three weeks later, the stu-
dents had to pass a small midterm exam.
Figure 1: Exemplary concept map from a student.
One week later, another collection of concept
maps yielded 19 student maps. Finally, immediately
after the end of the lecture and some weeks before
the final exam, there was a last test (post-test) that
was attended by 17 students. In the final exam, 13
students gave us their code number and hereby al-
lowed us to correlate their maps with their scoring in
the exam.
After the Bavarian government has shortened the
number of grades of the Gymnasium from 9 to 8
(from the type G9 to type G8) and introduced a new
compulsory subject of Informatics simultaneously in
2003, we will welcome two different age groups of
freshmen at the universities this year. The first group
has entered Gymnasium in 2003 (graduated from
G8), the second has started G9 at 2002. More inte-
restingly, there are 5 groups of freshmen regarding
their education in Informatics (shortly called EI-
groups): graduates from G9 didn’t have any regular
education in Informatics, graduates from G8 have
had, depending from their direction of study, 2 or 4
years of compulsory education and, eventually de-
pending from their choice of courses, 1 or 2 years of
elective courses.
Due to a specific program of our university, the
graduates from G9 were allowed to start their studies
already in summer 2011, while nevertheless, most of
them will enroll regularly at autumn 2011. Therefore
we have the singular opportunity to compare the
knowledge about Informatics of freshmen that be-
long to several different EI-groups. We are collect-
ing concept maps together with interviews dealing
with the ideas about typical topics and characteristic
working methods of Informatics and about the rea-
sons for their choice of Informatics as major. Our
goal is to find correlations between the declarative
knowledge (knowlets), the ideas about and the atti-
tudes towards Informatics and the EI-groups of the
students. In October 2010 we have already collected
concept maps and interviews from about 100 fresh-
men (G9). Some weeks ago, we have collected
another 250 sets, which we are scanning and digita-
lizing currently. After having completed their first
semester, we hope to collect a second generation of
concept maps from these 250 students in October,
and another 250 sets of maps and interviews from
the freshmen that will enroll at this time.
Additionally we are collecting concept maps in a
longitudinal study at a several classes (of grade 10
and 11) at a local Gymnasium (called GYS). The
goal is to detect if there are relevant differences in
the concept maps compared to the students at uni-
versity. Finally, we will collect concept maps from
the teachers using a specific internet based tool
(CoMapEd) that is under construction at the mo-
ment. Based upon the results of our teacher survey
from 2009 (see Mühling, Hubwieser & Brinda
2010), we expect about 300-400 teachers to draw a
concept map, using the same concept list CL as
described above.
5 DATA ANALYSIS
Before analyzing the CS1 maps, we normalized the
labels of the edges (which were freely chosen by the
students) in the following way: all verbs were trans-
formed to a standard form (first person singular
indicative), all isolated prepositions and articles
were deleted, all auxiliary verbs were removed,
isolated nouns or adjectives were deleted and all
multiplicity specifications (“some”, “many” etc.)
were removed. In the next step we categorized the
resulting labels from all surveys, following the rules
of qualitative text analysis (Mayring, 2000).
Based on this categorization, all associations
were scored by the lecturer of the course with points
(0 points for “totally incorrect”, 0.5 points for “part-
ly correct” and 1 point for “totally correct”). This
was performed by comparing the categories locally
to the objective expert map (see section 3), following
the technique “relational with master map” sug-
gested by (McClure et al., 1999).
5.1 Analysis of the Maps as a Whole
The results of the formal analysis of the CS1 maps
are described in detail in (Hubwieser and Mühling,
2011). First of all we detected that the students did
not use many different labels, although they were
totally free in choosing them. There were only 16
categories of association labels that were used in
more than 2% of all edges of at least one survey, and
KNOWPATS: PATTERNS OF DECLARATIVE KNOWLEDGE - Searching Frequent Knowledge Patterns about
Object-orientation
361

additionally their relative frequency was very similar
over the four surveys. If we set the threshold at 5%,
there remained only 5 different labels. 35% of all
associations over all surveys were labeled with a
word that was synonymous to contains or to has.
This result suggests that it is possible to restrict the
labeling to multiple choice without losing too much
information, which would ease automatic scoring
dramatically.
Concerning the graph theoretical measures we
found that the average number of correct edges in-
creased from 3.0 in the pretest to 11.0 in midtest2,
which showed that the students were learning in-
deed. We also found a significant high correlation
(0.68 with a p-value of 0.002) between the number
of correct edges in the first mid-test with the
achieved score in the midterm exam.
Figure 2: High-scored associations for Midtest 2.
Figure 3: Low-scored associations for Midtest 2
By selecting only the edges that were labeled
mostly correct (restricted to 9 the most important
concepts for object-orientation), we could identify
the concepts where the learning process was most
efficient (see Figure 2).
In contrary, the edges that were labeled mostly
incorrect show the problematic concepts (see Figure
3). More details are presented in (Hubwieser and
Mühling, 2011).
5.2 The Internal Structure of the Maps
As already explained in the introduction of this pa-
per, we are looking for patterns in the concept maps
that are frequently used by the students. We called
this patterns knowpats, which we define as induced
subgraphs of concept maps. We will look for fre-
quent knowpats in the student maps at four different
levels, which allows the reduction of the regarded
graphs to undirected ones:
1. General Level: The labels that have been given
by the students to the associations are ignored
(as long as there is any label). The existence of
any labeled association means that the student at
least knows that there is some connection be-
tween the two concepts (Kinchin et al., 2000).
2. Scoring: only edges that have a score > 0 are
taken into account, thus taking into considera-
tion all totally correct as well as all partly cor-
rect edges.
3. Total Correctness: Only the totally correct
edges are considered.
As we suggest that the students get their know-
ledge mainly from the material that was presented in
the course, the assumed arities of associations that
were suggested by these texts (see table 1) restrict
the range of the size of the expected knowpats from
2 to 5.
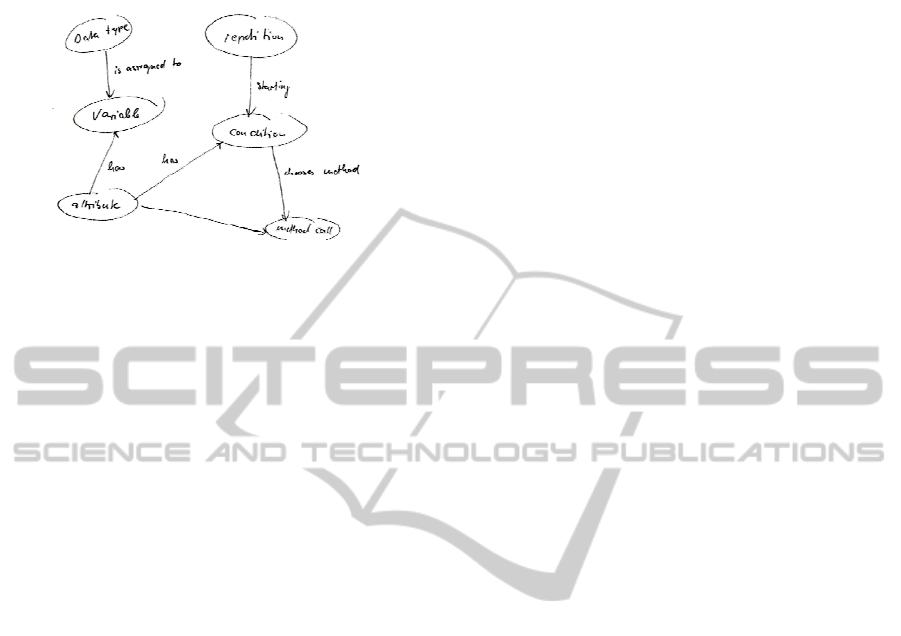
Figure 4: Knowpat suggested by knowledge element (*).
For the search we will apply the AcGM Algo-
rithm of (Inokuchi et al., 2000), which can be
adapted to our purposes and environment. It extracts
frequently occurring subgraphs (in our case know-
pats) from a large database of graphs (in our case
concept maps) and is especially suited for finding
large subgraphs, as it successively builds larger and
larger candidate subgraphs and checks how often
they occur in the database.
We could simply use the AcGM algorithm for
the task. However, as we’re dealing with a problem
that contains the NP-complete subgraph-iso-
morphism problem, it might be worthwhile to adapt
the algorithm for our specific needs, in order to
achieve somewhat better running times in real-life
scenarios.
Firstly, concept maps are typically directed,
small and sparse graphs. The list of concepts puts a
MT2
generalisation
sub-class
class object
method call
method
association
attribute
specialisation
MT2
generalisation
sub-class
class
inheritance
object
method call
method
association
attribute
polymorphism
instanciation
object
attribute value
state
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
362

bound on the number of vertices, so those will never
exceed 50 at most. Additionally, even if the graphs
are not always strictly DAGs, they tend to resemble
directed trees (or forests) and can be considered
sparse graphs in which the number of edges grows at
most linear with the number of nodes.
Secondly, as outlined above, we’re only con-
cerned with subgraphs of size 2 to 5 nodes. As there
are only three knowledge elements with an arity of
5, we might exclude these from the analysis, leaving
us with subgraphs with at most 4 nodes. The nice
thing about this is that there are well established
algorithms for finding subgraph-isomorphisms with
3 and 4 nodes (e.g. the VF2 algorithm by Cordella et
al., 2004). For 2 nodes the isomorphic class of a
subgraph is trivially decided by using the edge count
of the induced subgraph. That means, we can avoid
the coding and normalizing of the adjacency matric-
es that’s a big part of AcGM and instead use existing
algorithms for those sub-tasks.
Thirdly, we’re interested in connected subgraphs
only. A missing connection can never serve as evi-
dence in favor of a knowpat since we cannot infer
anything from it, by itself.
For the analysis, we treat the concept maps as
undirected graphs, as the direction is only dependent
on the chosen edge label and not on the concepts
involved. Multiple edges between concepts will then
be collapsed into one. The graphs may still contain
self-loops however. Typically, isomorphism check-
ing relies on simple graphs (as does the AcGM algo-
rithm), so we’ll either have to ignore self-loops or
transform the concept maps into a simple graph first.
As they may very well contain valid statements (e.g.
object - communicates with - object) they should not
be ignored. Transformation is easily done by adding,
for each self-loop
v, v
∈E, a new node with the
same label as v and replacing the loop with an edge
to the new node (keeping the label of the edge).
In the worst case, this doubles the size of our
graphs, but in real life, the data typically only exhibit
a very small number of self-loops.
After this step, we have a database of simple,
undirected graphs. The main algorithm based on the
ideas of AcGM works as follows:
Starting with the only connected isomorphism
class of size 2 (two nodes connected by an edge), we
count the frequency for each pair of nodes in the
database. This can easily be done by simple counting
and comparing the entries in the adjacency matrices.
For example, the following associations were the
most frequently used at the CS1 course among 1.665
associations in 115 maps: (class, object) with 58
occurrences, (data, data type) and (object, attribute)
with 44 occurrences each.
Starting from this, we get a list of candidates that
have a support higher than a chosen threshold. For
sparse graphs, this list will contain O(|V|) entries.
From these frequently occurring size 2 sub-
graphs, we can create the list of candidate size 3
subgraphs that need to be checked. According to the
observation in AcGM, those must be formed by
combining two subgraphs of size 2 that have a high
enough support and that share exactly one node. We
can simply do a pairwise join of the size 2 candi-
dates and extract all those with 3 nodes. All those
candidates exist in exactly two forms: Either with 2
edges, or with 3.
We count the frequency of those candidates in
our database using the VF2 algorithm. Finally, the
list of frequently occurring size 3 subgraphs leads to
a list of candidate size 4 subgraphs, again by recom-
bination of two size 3 graphs that share exactly 2
nodes. Those too, exist in two forms, one in which
the two non-shared nodes are neighbors and one in
which they’re not.
This leaves us with a final list of at most O(
|
V
|
)
entries. However in real life we expect the lists to be
much shorter. The frequency of those candidates
will then be found again using the VF2 algorithm.
While there really is no way around the combina-
torial complexity when searching the subgraphs in
the database, this approach at least only creates a
small subset of all possible size 3 or 4 subgraphs
according to what actually can be present in the
database. As the algorithm is in a certain way more
sensitive to the size of the graphs than to the number
of graphs, we should be able to handle the large
amounts of data that arise in the current and subse-
quent studies.
6 CONCLUSIONS
We presented a method that allows searching for
small, frequently recurring subgraphs in a database
of concept maps. We take those subgraphs as indica-
tors for recurring structures in declarative know-
ledge in computer science (called knowpats). Find-
ing knowpats will allow us a deeper understanding
of the prerequisite knowledge that a competent CS
student needs to possess. As we have collected many
comparable maps from freshmen of CS, we hope to
find such patterns there. Once candidate patterns are
identified, the next step will be to validate them (for
example by using a broader, more diverse group of
students as the basis) and to investigate how those
KNOWPATS: PATTERNS OF DECLARATIVE KNOWLEDGE - Searching Frequent Knowledge Patterns about
Object-orientation
363

candidates correspond to the actual abilities and the
biography of the students. Clearly, knowing about
the internal structures of CS knowledge is also an
effective way of evaluating and designing CS
courses.
REFERENCES
Albert, D & Steiner, C. M. 2005, 'Empirical Validation of
Concept Maps: Preliminary Methodological Consider-
ations' in Proceedings of the Fifth IEEE International
Conference on Advanced Learning Technologies
(ICALT’05), ed IEEE.
Anderson, J. R. 2005, Cognitive psychology and its impli-
cations. John R. Anderson, Worth Publishers, New
York.
Anderson, L. W. 2009, A taxonomy for learning, teaching,
and assessing. A revision of Bloom's taxonomy of
educational objectives, Longman, New York.
Armstrong, D. J. 2006, 'The quarks of object-oriented
development', Commun. ACM, vol. 49, pp. 123–128.
Cordella, L. P., Foggia, P., Sansone, C. & Vento, M. 2004,
'A (sub)graph isomorphism algorithm for matching
large graphs', Pattern Analysis and Machine Intelli-
gence, IEEE Transactions on, vol. 26, no. 10, pp.
1367–1372.
Dominguez, A. K. (2010). Data Mining for Individualised
Hints in e-Learning. In Proceedings of the interna-
tional conference of educational data mining (EDM
2010). Pittsburgh .
Goldsmith, T. E. & Davenport, D. M. 1990, 'Assessing
structural similarity of graphs' in Pathfinder associa-
tive networks, Ablex Publishing Corp, pp. 75–87.
Hubwieser, P. & Mühling, A. 2011, 'What Students
(should) know about Object Oriented Programming' in
ICER’11: Proceedings of the 7th International Com-
puting Education Workshop. August 8–9, Providence,
Rhode Island, USA, ed ACM, pp. To appear.
Hubwieser, P., Spohrer, M., Steinert, M. & Voß, S. 2008,
Algorithmen, objektorientierte Programmierung,
Zustandsmodellierung. Schülerbuch - Jahrgangsstufe
10, Klett, Stuttgart.
Inokuchi, A., Washio, T. & Motoda, H. 2000, 'An Apriori-
Based Algorithm for Mining Frequent Substructures
from Graph Data'. Principles of Data Mining and
Knowledge Discovery, 4th European Conference,
PKDD 2000, Lyon, France, September 13-16, 2000,
Proceedings, eds DA Zighed, HJ Komorowski & JM
Zytkow, Springer, pp. 13–23.
Kinchin, I. M., Hay, D. B. & Adams, A. 2000, 'How a
qualitative approach to concept map analysis can be
used to aid learning by illustrating patterns of concep-
tual development', Educational Research, vol. 42, no.
1, pp. 43–57.
Madhyastha, T., & Hunt, E. (2009). Mining diagnostic
assessment data for concept similarity. Journal of
Educational Data Mining, 1(1), 72–91.
Mayring, P. 2000, Qualitative Content Analysis. Available
from: http://qualitative-research.net/fqs/fqs-e/2-00inha
lt-e.htm.
McClure, J. R., Sonak, B. & Suen, H. K. 1999, 'Concept
map assessment of classroom learning: Reliability, va-
lidity, and logistical practicality', Sci Teach, vol. 36,
pp. 475\textendash492.
Mons, B., Ashburner, M., Chichester, C., van Mulligen,
E., Weeber, M., den Dunnen, J., van Ommen, G., Mu-
sen, M., Cockerill, M., Hermjakob, H., Mons, A.,
Packer, A., Pacheco, R., Lewis, S., Berkeley, A., Mel-
ton, W., Barris, N., Wales, J., Meijssen, G., Moeller,
E., Roes, P., Borner, K. & Bairoch, A. 2008, 'Calling
on a million minds for community annotation in Wi-
kiProteins', Genome Biology, vol. 9, no. 5, pp. R89.
Mühling, A., Hubwieser, P. & Brinda, T. 2010, 'Exploring
Teachers‘ Attitudes Towards Object Oriented Model-
ling and Programming in Secondary Schools'. ICER
‘10: Proceedings of the Sixth International Workshop
on Computing Education Research, ed ACM, ACM,
New York, NY, USA, pp. 59–68.
Norman, D. A. 1983, 'Some observations on mental mod-
els' in Mental models: eds D Gentner & AL Stevens,
Lawrence Erlbaum Associates, Hillsdale, NJ, pp. 7–
14.
Pedroni, M. & Meyer, B. 2010, 'Object-Oriented Modeling
of Object-Oriented Concepts' in Teaching fundamental
concepts of informatics. 4th International Conference
on Informatics in Secondary Schools - Evolution and
Perspectives, ISSEP 2010, Zurich, Switzerland, Janu-
ary 13-15, 2010; proceedings, eds J Hromkovic, R
Královic & J Vahrenhold, Springer, Berlin, pp. 155–
169.
Romero, C., Romero, J. R., Luna, J. M., & Ventura, S.
(2010). Mining rare association rules from e-learning
data. In Proceedings of the International Conference
of Educational Data Mining (EDM 2010). Pittsburgh
(pp. 171–180).
Sanders, K., Boustedt, J., Eckerdal, A., McCartney, R.,
Moström, J. E., Thomas, L. & Zander, C. (eds.) 2008,
Student understanding of object-oriented program-
ming as expressed in concept maps, ACM, New York,
NY, USA.
Schank, R. C. & Abelson, R. P. 1977, Scripts, Plans,
Goals and Understanding: an Inquiry into Human
Knowledge Structures, L. Erlbaum, Hillsdale, NJ.
Shavelson, R. J. & Ruiz-Primo, M. A. 1999, 'On the psy-
chomentrics of assessing science understanding.' in
Assessing science understanding, eds J Mintzes, JH
Wandersee & JD Novak, Academic Press, San Diego,
pp. 304–341.
Vanides, J., Yin, Y., Tomita, M. & Ruiz-Primo Maria
Araceli 2005, 'Using Concept Maps in the Classroom',
Vol. 28, No. 8, Summer 2005, Science Scope, vol. 28,
no. 8, pp. 27–31.
KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval
364
