ROBUST SEMANTIC WORLD MODELING BY BETA
MEASUREMENT LIKELIHOOD IN A DYNAMIC
INDOOR ENVIRONMENT
Gi Hyun Lim
1
, Chuho Yi
1
, Il Hong Suh
2
and Seung Woo Hong
3
1
Department of Electronics & Computer Engineering, Hanyang University, Seoul, Korea
2
College of Information and Communications, Hanyang University, Seoul, Korea
3
Department of Intelligent Robot Engineering, Hanyang University, Seoul, Korea
Keywords:
Robust knowledge instantiation, Semantic world modeling, Beta measurement likelihood.
Abstract:
In this paper, a semantic world model represented by objects and their spatial relationships is considered to
endow service robots. In the case of using commercially available visual recognition systems in dynamically
changing environments, semantic world modeling must solve problems caused by imperfect measurements.
These measurement result from variations caused by moving objects, illumination changes, and viewpoint
changes. To build a robust semantic world model, the measurement likelihood method and spatial context
representation are addressed to deal with the noisy sensory data, which are handled by temporal confidence
reasoning of statistical observation and logical inference, respectively. In addition to the representation of a
semantic world model for service robots, formal semantic networks can be exploited in representations that
allow for interaction with humans and sharing and re-using of semantic knowledge. The experimental results
indicate the validity of the presented novel method for robust semantic mapping in an indoor environment.
1 INTRODUCTION
Semantic world modeling is considered to provide
service robots with the ability to interact with humans
and share or re-use semantic knowledge (Thielscher,
2000), (Hertzberg and Saffiotti, 2008). In the real en-
vironment, a semantic world model affords to repre-
sent a dynamically changing world. Significant prob-
lems are caused by imperfect measurements, which
result from variations caused by moving objects, in-
cluding humans, illumination changes, and viewpoint
changes (Thrun, 2002). Even if commercially avail-
able visual recognition systems are used (Munich
et al., 2005), many imperfect measurements remain
false positives and false negatives due to mismatches
that result in false semantic world models. Relatively
speaking, false positive results not a serious imped-
iment to the visual recognition domain but can be
problematic for formal logics. Insufficient facts due
to false negative results can be corrected by additional
true positive results, but erroneous facts due to false
positive results will result in false reasoning conse-
quences; this generates a vicious cycle, and errors are
difficult to correct even with additional true negative
results.
To build a robust semantic world model, the mea-
surement likelihood function and spatial context rep-
resentation are addressed to deal with the noisy sen-
sory data, which are handled by temporal reasoning
rules (Lim and Suh, 2010) using statistical observa-
tion (Park et al., 2009) and logical inference, respec-
tively. A measurement likelihood function based on
beta distribution is proposed to estimate the confi-
dence of a sequence of sensory observations. The
measurement likelihood function converts stochasti-
cally to an object recognition likelihood by match-
ing between the model and observations. The logi-
cal modeling of temporal rules infers spatial relation-
ships so as to check the temporal relations among ob-
servation time intervals (Allen, 1991). In addition to
the representation of a semantic world model for a
service robot, formal semantic networks (Suh et al.,
2007), (Lim et al., 2011) can be exploited in repre-
sentations that allow for interaction with humans and
sharing and re-using of semantic knowledge (Yi et al.,
2009b), (Yi et al., 2009a).
This paper is organized as follows: In the next sec-
tion, overall architecture for semantic world modeling
and localization is discussed. Formal representation
of a semantic world model is described in section 3.
311
Lim G., Yi C., Suh I. and Woo Hong S..
ROBUST SEMANTIC WORLD MODELING BY BETA MEASUREMENT LIKELIHOOD IN A DYNAMIC INDOOR ENVIRONMENT.
DOI: 10.5220/0003690503110316
In Proceedings of the International Conference on Knowledge Engineering and Ontology Development (KEOD-2011), pages 311-316
ISBN: 978-989-8425-80-5
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Sections 4 and 5 explain the measurement likelihood
function to determine false positive and false negative
results and temporal confidence reasoning to instan-
tiate objects and their spatial relationships, respec-
tively. In section 6, experimental results are presented
to show the validity of the presented novel method.
Finally, in section 7, the conclusion and consideration
are discussed.
2 OVERALL ARCHITECTURE
Figure 1 shows the overall architecture for semantic
world modeling and localization. When there is an
observation from the viewpoint of a service robot, its
features are matched with the features of the model
in object database. The likelihood of measurement
is estimated using the stochastic method. By obser-
vation measurement and control, a local metric map
is built from the viewpoint of the robot. A spatial
context reasoner infers spatial relationships between
objects from the viewpoint of the reference object,
which is usually the object that if found first in the
local area. The viewpoint transformation from ego-
centric to allocentric representation can be accom-
plished using logical rules for movement and rotation.
When a robot moves to an-other area and finds an
object, two areas are linked topologically. By using
a topological-semantic distance map, global localiza-
tion is made possible through the object and the spa-
tial object contexts. In addition, the localization is
processed more specifically and locally based on the
observed object information around the node. Within
the overall framework, the present study concentrates
on robust semantic mapping, which enables humans
to interact with robots.
Topological
semantic
distance map
Spatial context
Reasonor
Local metric map
Semantic Navigation
for active-localization
Semantic
Localization
Control
Observation
Measurement
Likelihood
Object
Database
Robot pose
Figure 1: Overall architecture for semantic world modeling
and localization.
3 REPRESENTATION OF A
SEMANTIC MAP
3.1 Topological-semantic Distance Map
A topological-semantic distance map is proposed to
model space by means of ontology, which ensures
that only sound and complete data are asserted and
propagated with ontology inference. The proposed
topological-semantic distance map, which consists of
spatial object contexts and spatial robot contexts, in-
cludes two types of maps: a transient local metric map
and a permanent topological semantic map. A met-
ric map is built using observation measurements. A
topological-semantic map includes nodes and edges
for global topological representation between nodes,
objects, and their spatial relationships for local se-
mantic representation. A node is one of the compo-
nents of a global topological map that plays the role
of a standard and contains information on the spatial
object contexts. The spatial robot contexts used in
the proposed semantic representation can explain an
approximate distance and bearing from one assigned
node to another. We describe how an approximate
qualitative distance is the node-to-node (n-n) distance
context and the qualitative bearing is the n-n bear-
ing context. Spatial relationships are more concerned
with the viewpoints of objects than the robot’s own
observation viewpoints. The allocentric representa-
tion is converted egocentrically in the case of localiza-
tion or navigation (Yi et al., 2009b), (Yi et al., 2009a).
3.2 Spatial Object Contexts
Figure 2 shows a semantic representation con-
sisting of observed objects and their respective
spatial symbols. The spatial context includes
distance, bearing, and relationship contexts. The
r-o distance context denoted by s
r
is the dis-
tance of the object from the robot. Each distance
context is represented by one of a set of dis-
tance symbols, that is, s
r
= {nearby,near, f ar}.
The r-o bearing context denoted by s =
{ f ront,le f t f ront,le f t,le f trear,rear,rightrear,right,
right f ront} is the bearing of the object relative to the
robot. The o-o relationship context denoted by s =
{le f t f ar, le f tnear,le f tnearby,rightnearby,rightnear,
right f ar} is the relationship among objects.
Table 1 shows a semantic representation using
symbols for all the spatial contexts in Fig. 2. Our
robot localization application finds the position of the
robot using only these types of semantic representa-
tions with qualitative metric data.
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
312

Object(Object_1)
Object(Object_2)
Object(Object_3)
Figure 2: Spatial object contests, spatial relationships be-
tween object-based local coordinates.
Table 1: Semantic representation including all the spatial
object contexts in Fig. 2.
State Semantic representation
Previous
state
nearby(o1, Robot), left front(o1, Robot),
right near(o1, o2), right far(o1, o3), far(o2,
Robot), front(o2, Robot), left near(o2, o1),
right near(o2, o3), far(o3, Robot), right
front(o3, Robot), left far(o3, o1), left
near(o3, o2)
Current state near(o2, Robot), left front(o2,Robot), right
far(o2, o3), nearby(o3, Robot), right
front(o3, Robot), left far(o3, o2)
4 MEASUREMENT LIKELIHOOD
FUNCTION
The measurements of visual observation can be in-
stantiated as ontology for the representation of the
topological-semantic map, which ensures that only
sound and complete data are asserted and propagated
with ontology inference. Noisy sensor data, such as
false positives and true negatives, should be filtered
for robust semantic mapping. In the case of false pos-
itives, the properties are illogical, for instance, a mis-
classified object may make erroneous spatial relation-
ships. Moreover, inferred erroneous facts will result
in false consequences for reasoning; this generates a
vicious cycle, and errors are difficult to correct, even
with additional true negative results.
To address the failure of knowledge instantiation,
a measurement likelihood function and a robust se-
mantic knowledge instantiation rule is proposed to
ensure the logical rigidness of robot knowledge in-
stances.
4.1 Beta Measurement Likelihood
Function
Noisy data are the result of dynamic factors and view-
point changes. Similar to the LeTO
2
function (Park
et al., 2009), the measurement likelihood function is
introduced on the basis of beta distribution. Beta dis-
tribution can be in the form of well-applied successive
independent Bernoulli trials. Each feature point of vi-
sual observation is regarded as an independent trial
to determine matching. To model the measurement
likelihood function, a cumulative distribution func-
tion (cdf) of beta distribution is applied. The cdf is
an S-shaped function in cases where al pha and beta
are more than 1. Given s successes in n condition-
ally independent trials with probability p, p should be
estimated as (s + 1)/(n + 2). This estimate may be
regarded as the expected value of the posterior distri-
bution over p, namely Beta(s + 1, n - s + 1), and then
it is observed that p generated s successes in n trials.
f (x;α, β) =
1
B(α,β)
x
α−1
(1 − x)
β−1
= B
x
(α,β), (1)
F(n; α,β) =
B
r
(α,β)
B(α,β)
= I
r
(α,β). (2)
For registration, every trained object image is se-
lected at each node by the user, and feature points of
captured images are stored in the database. During
matching for mapping or localization, the features ex-
tracted from an image taken at the current location of
the robot are matched with those extracted from each
reference image in a pre-built database.
A formal description of the beta measurement
likelihood function is as follows:
ML
β
(r) = F(r; α,β)
= F(r;s + 1, n − s + 1) =
B
r
(s+1,n−s+1)
B(s+1,n−s+1)
= I
r
(s + 1,n − s + 1)
where, s = average number of matched keypoints,
n = average number of model keypoints,
r = matching ratio between model features
and currently observed features,
α = s + 1,
β = n − s + 1.
4.2 Likelihood Confidence Interval
(LCI)
Confidence of recognition is determined by an likeli-
hood interval-counter (γ) from the measurement like-
lihood for each object recognition result. An interval-
counter for each object is defined on the basis of the
ROBUST SEMANTIC WORLD MODELING BY BETA MEASUREMENT LIKELIHOOD IN A DYNAMIC INDOOR
ENVIRONMENT
313

confidence law of inertia, whereby a knowledge in-
stance is assumed to persist unless there is confidence
to believe otherwise. If the measurement likelihood
of object A is x
A
, then (1-x
A
) is the probability that
the recognition data for A can be false. From that,
(1-x
A
)
γ
A
can be calculated to define probability when
the values of γ
A
consecutive data are all false. If the
result of (1-x
A
)
γ
A
is less than 5% (0.05), then it can
be said that the data have been obtained within a con-
fidence interval (1.96σ, P = 0.05) of the 95% confi-
dence level. For example, if the measurement likeli-
hood of object A is 80%successively, the recognition
failure rate of object A might be 20% (0.2). The result
rate of recognition failure of two consecutive obser-
vations is 4% (0.04) and 4% is beyond the 95% con-
fidence interval(P = 0.05), so γ of object A is 2. At
that time, the instance of object A is created and vice
versa. The likelihood interval-counter using β likeli-
hood distribution can be represented as follows:
γ
β
= min{γ ∈ I|
n
∏
i=1
(1 − x
obj
) ≤ P}, (3)
where P = 0.05 = 1 − 95% confidence level.
5 TEMPORAL CONFIDENCE
REASONING
According to continuous observations from robot
movement, object instances might be created or
deleted whether certain number of consecutive obser-
vation likelihoods exceed the likelihood confidence
interval. Time intervals of object instances which ex-
ist or not is determined by the durations between the
changes of confidence. Temporal relations between
intervals are inferred using temporal reasoning. The
temporal relation was first proposed by Allen (Allen,
1991) and represents temporal relations using before,
after, meets, met-by, overlaps, overlapped-by, and so
on. Table 2 lists the rules of temporal reasoning to
show the end point relations between two intervals.
In the table, ob j
1
and ob j
2
are object instances, in-
tervals a
l
, a
m
and a
n
include start point a
s
and end
point a
e
. If two intervals meet or overlap, then they
are merged into one interval. The merged interval be-
gins at the start point of the former and ends at the
end point of the latter. Temporal confidence reason-
ing (TCR) is based on the assumption that recognized
objects cannot go away and come back within a single
time interval.
When an object instance of A is registered, if other
objects are also considered to be true positive in-
stances and to have a temporal relation of overlapped
Table 2: Rules of Temporal Confidence Reasoning.
Temporal Relation End Point Relations
if ob j
1
= ob j
2
and a
ob j
1
l
meets a
ob j
2
m
⇒ a
ob j
1
n
if ob j
1
= ob j
2
and a
ob j
2
l
met by a
ob j
1
m
⇒ a
ob j
1
n
a
s
l
< a
e
l
= a
s
m
<
a
e
m
⇒ a
s
l
= a
s
n
<
a
e
m
= a
e
n
if ob j
1
= ob j
2
and a
ob j
1
l
overlaps a
ob j
2
m
⇒ a
ob j
1
n
if ob j
1
= ob j
2
and
a
ob j
2
l
overlapped
by
a
ob j
1
m
⇒ a
ob j
1
n
a
s
l
< a
s
m
< a
e
l
<
a
e
m
⇒ a
s
l
= a
s
n
<
a
e
m
= a
e
n
with object A, then spatial relations among the objects
can be inferred. For instance, Fig. 3 presents a set
of spatial relations between objects A and B. When
the is-interval of object B is considered to be true, the
temporal relation between a
+
m
and b
+
m
is considered
to be an overlap. Then, the spatial relation between
them can be reasoned and set using spatial reasoning.
All object instances and their spatial relations can be
registered in the instance database.
a
+
0.8
b
+
0.7 0.7
0.6 0.8
Spatial Context
between Obj
A
and Obj
B
0.7
Observation
Likelihood
Intervals of Obj
a
Observation
Likelihood
Intervals of Obj
b
Figure 3: Temporal reasoning of spatial relations between
object A and B, in which ‘+’ denotes positive instance.
6 EXPERIMENTAL RESULTS
A Pioneer 3 AT robot carrying a single consumer-
grade camera was driven around an indoor environ-
ment (14 × 10 m) to evaluate the performance of the
proposed semantic mapping.
Figure 4: Examples of trained object(landmark) images.
Figure 4 shows examples of trained object images
selected by the user. The camera observed 9 objects
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
314

during its travel around the indoor environment. Dis-
tinctive objects such as a printer, a refrigerator,
drawers, etc were used for object recognition.
Proposed method Threshold=10 Threshold=15
0.0
0.4
0.8
Ratio
True Positive
True Negative
False Positive
False Negative
Precision
Recall
Figure 5: Experimental results.
Figure 5 summarizes the results of a three-
approach, cross-validation experiment using the pro-
posed method with a threshold of 10 and 15 correct
matches. In many cases, object recognition by an
Evolution Robotics Vision system was used with a
threshold of 10 correct matches.
In order to confirm our results, we evaluated the
performance of the system measuring its effectiveness
by means of true positive, true negative, false positive,
false negative, Precision, and Recall. We present the
results relative to precision and false positive, which
indicate overall performance. Figure 5 show that pre-
cision increases up to a level of 1. It is observed that
all false positives were successfully removed from the
recognition results. The experimental results reveal
that the proposed method makes it possible to robustly
register object instances even with an imperfect vision
sensor. However, in the proposed method, false nega-
tives cause the recall to decrease somewhat. Most of
the false negatives in our method register at early in-
stantiation. On the other hand, once a robust semantic
map is built, false negatives also decrease at localiza-
tion or update (Lim and Suh, 2010), (Yi et al., 2009b),
(Yi et al., 2009a).
Figure 6, Figure 7, and Figure 8 show experimen-
tal results of temporal reasoning to check the validity
of the relationships between intervals and statistical
reasoning to determine the LCI of object recognition,
where the blue line represents the trajectory which is
measured using odometry.
Figure 9 illustrates a topological-semantic dis-
tance map consisting of 4 nodes (blue, rectangle) and
9 objects (pink, circle). Solid lines between nodes are
the edges that represent n-n contexts of distances and
bearings. The blue lines denote the r-o context and
the red lines represent the o-o context.
Figure 6: Experimental environment composed of nine ob-
jects.
Figure 7: Specific example of mapping on imperfect sens-
ing data.
Figure 8: Result of mapping using temporal and statistical
reasoning.
7 CONCLUDING REMARKS
In this paper, we proposed a robust semantic map-
ping method for use under conditions of imperfect
object recognition. The method uses beta measure-
ment likelihood statistical reasoning to determine the
confidence interval of object recognition and tempo-
ROBUST SEMANTIC WORLD MODELING BY BETA MEASUREMENT LIKELIHOOD IN A DYNAMIC INDOOR
ENVIRONMENT
315

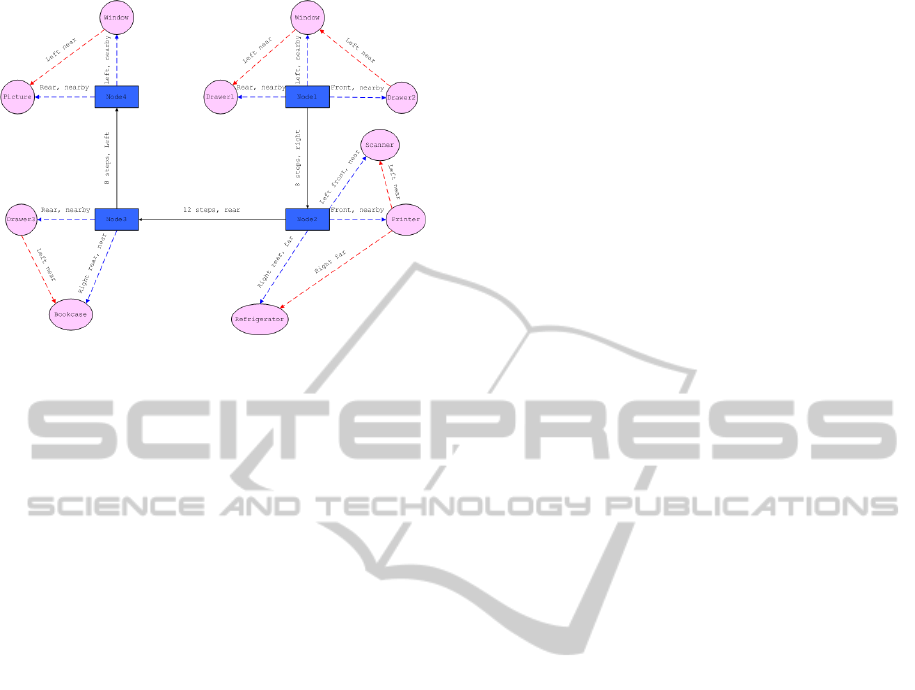
Figure 9: Result of topological-semantic distance-map
building.
ral reasoning to check the validity of relationships be-
tween intervals, and represent ontological spatial re-
lations between objects and the semantic map. De-
termining failures from unreliable object recognition
makes it possible to dependably instantiate semantic
knowledge. In our novel approach, the robot verifies
the recognized objects as true or not. The experi-
mental results indicate that all false positives in the
recognition results were corrected. Therefore, a ro-
bust topological-semantic distance map, consisting of
nodes, objects, and their relationshipscan be built for
application in service robots.
ACKNOWLEDGEMENTS
This work was supported for the Intelligent Robotics
Development Program, one of the 21st Century
Frontier R&D Programs funded by the MKE(Korea
Ministry of Knowledge Economy), and partially
supported by the MKE, Korea, under the Human
Resources Development Program for Convergence
Robot Specialists support program supervised by
the NIPA(National IT Industry Promotion Agency)
(NIPA-2011-C7000-1001-000x).
REFERENCES
Allen, J. (1991). Planning as temporal reasoning. In Pro-
ceedings of the Second International Conference on
Principles of Knowledge Representation and Reason-
ing, volume 13, pages 25–45. Citeseer.
Hertzberg, J. and Saffiotti, A. (2008). Editorial: Using
semantic knowledge in robotics. Robotics and Au-
tonomous Systems, 56(11):875–877.
Lim, G. H. and Suh, I. H. (2010). Robust robot knowledge
instantiation for intelligent service robots. Intelligent
Service Robotics, pages 115–123.
Lim, G. H., Suh, I. H., and Suh, H. (2011). Ontology-
based unified robot knowledge for service robots in
indoor environments. Systems, Man and Cybernetics,
Part A: Systems and Humans, IEEE Transactions on,
41(3):492 –509.
Munich, M., Ostrowski, J., and Pirjanian, P. (2005). ERSP:
a software platform and architecture for the ser-
vice robotics industry. In 2005 IEEE/RSJ Interna-
tional Conference on Intelligent Robots and Systems,
2005.(IROS 2005), pages 460–467.
Park, Y., Suh, I., and Choi, B. (2009). Bayesian robot lo-
calization with action-associated sparse appearance-
based map in a dynamic indoor environment. In Pro-
ceedings of the 2009 IEEE/RSJ international confer-
ence on Intelligent robots and systems, pages 3459–
3466. IEEE Press.
Suh, I. H., Lim, G. H., Hwang, W., Suh, H., Choi, J. H.,
and Park, Y. T. (2007). Ontology-based multi-layered
robot knowledge framework (OMRKF) for robot in-
telligence. In IEEE/RSJ International Conference
on Intelligent Robots and Systems, 2007. IROS 2007,
pages 429–436.
Thielscher, M. (2000). Representing the Knowledge of a
Robot. In Principles of knowledge representation and
reasoning: Proceedings of the Seventh International
Conference (KR2000), Breckenridge, Colorado, April
12-15 2000, pages 109–120. Morgan Kaufmann Pub.
Thrun, S. (2002). Probabilistic robotics. Communications
of the ACM, 45(3):57.
Yi, C., Suh, I. H., Lim, G. H., and Choi, B. U. (2009a).
Active-semantic localization with a single consumer-
grade camera. In Proceedings of the 2009 IEEE inter-
national conference on Systems, Man and Cybernet-
ics, pages 2161–2166. IEEE Press.
Yi, C., Suh, I. H., Lim, G. H., and Choi, B. U. (2009b).
Bayesian robot localization using spatial object con-
texts. In Proceedings of the 2009 IEEE/RSJ interna-
tional conference on Intelligent robots and systems,
pages 3467–3473. IEEE Press.
KEOD 2011 - International Conference on Knowledge Engineering and Ontology Development
316