CMAC STRUCTURE OPTIMIZATION WITH Q-LEARNING
APPROACH AND ITS APPLICATION
Weiwei Yu
1
, Kurosh Madani
2
and Christophe Sabourin
2
1
School of Mechatronic Engineering, Northwestern Polytechnical University, Youyi Xilu 127hao, 710072, Xi'an, P.R.China
2
Images, Signals and Intelligence Systems Laboratory (LISSI / EA 3956), UPEC University
Senart-Fontainebleau Institute of Technology, Bât. A, Av. Pierre Point, F-77127, Lieusaint, France
Keywords: CMAC neural network, Structural parameters, Q-learning, Structure optimization.
Abstract: Comparing with other neural networks based models, CMAC is successfully applied on many nonlinear
control systems because of its computational speed and learning ability. However, for high-dimensional
input cases in real application, we often have to make our choice between learning accuracy and memory
size. This paper discusses how both the number of layer and step quantization influence the approximation
quality of CMAC. By experimental enquiry, it is shown that it is possible to decrease the memory size
without losing the approximation quality by selecting the adaptive structural parameters. Based on Q-
learning approach, the CMAC structural parameters can be optimized automatically without increasing the
complexity of its structure. The choice of this optimized CMAC structure can achieve a tradeoff between
the learning accuracy and finite memory size. At last, the application of this Q-learning based CMAC
structure optimization approach on the joint angle tracking problem for biped robot is presented.
1 INTRODUCTION
The Cerebellar Model Articulation Controller
(CMAC) is a neural network (NN) based model
proposed by Albus inspiring from the studies on the
human cerebellum (J. S. Albus, 1975). Because of
the advantages of simple and effective training
properties and fast learning convergence, CMAC has
been used in many real-time control systems, pattern
recognition and signal processing problems
successfully. However, besides its attractive
features, the main drawback of the CMAC network
in realistic applications is related to the required
memory size. For the input space greater than two,
on one hand, in order to increase the accuracy of the
control the chosen quantification step must be as
small as possible which will cause the CMAC’s
memory size become quickly very large; on the
other hand, generally in real world applications the
useable memory is finite or pre-allocated. Therefore,
for high-dimensional input cases we often have to
make our choice between accuracy and memory
size.
To solve the problem relating to the size of the
memory, generally these efforts can be classified
into three main approaches. The first theoretical
aspect is developed on how to modify the input
space quantization (Hung-Ching Lu et al., 2006); (S.
D. Teddy et al., 2007). This is based on the idea of
the quantization method of input space is a decisive
factor of the memory utilization and the more
intervals we quantized, the more precise learning we
will obtain. However, not only the quantization step
but also number of layers determines the learning
preciseness and the required memory size. The
second approach involves the use of multilayered
CMACs of increasing resolutions, demonstrating the
properties of generating and pruning the input layers
automatically (A. Menozzi and M. Chow, 1997);
(Chih-Min Lin and Te-Yu Chen, 2009).
Nevertheless they lack the theoretical proof of the
system’s learning convergence, which is a desirable
attribute for control and function approximation
tasks. The third orientation which is most popular
focuses on incorporating fuzzy logic into CMAC to
obtain a new fuzzy neural system model called fuzzy
CMAC (FCMAC) to alleviate the required memory
size (M. N. Nguyen et al., 2005); (Daming Shi et al.,
2010). Yet, it rises new problem on how to design an
optimal fuzzy sets.
In the above CMAC literatures, there is no one
related to the tradeoff problem of limited memory
283
Yu W., Madani K. and Sabourin C..
CMAC STRUCTURE OPTIMIZATION WITH Q-LEARNING APPROACH AND ITS APPLICATION.
DOI: 10.5220/0003694102830288
In Proceedings of the International Conference on Neural Computation Theory and Applications (NCTA-2011), pages 283-288
ISBN: 978-989-8425-84-3
Copyright
c
 2011 SCITEPRESS (Science and Technology Publications, Lda.)

size and learning quality. It is traditionally thought
that the more exquisitely the input space is divided,
the more accurately the output results of CMAC can
be obtained. However, this will certainly cause
quickly increasing of memory size, if we do not
develop more complex CMAC structure, since the
simplicity of structure play an important role in the
on-line application of neural network. In fact, by
experimental study of approximation examples, in
which several high-dimension functions were
selected and several combinations of structural
parameters were tested, we found that the learning
preciseness and the required memory size are
determined by both of the quantization step and
number of layers. Thus, adaptive choice of these
structural parameters may overcome the above
primary limitation. Our goal is that a CMAC
structure can be optimized automatically for a given
problem. In this way, it is possible to decrease the
memory size according to the desired performance
of the CMAC neural network.
The paper is organized as follows: In section 2,
CMAC model and its structure parameters are
concisely overviewed. Section 3 presents the
experimental study of the influence of structural
parameters on the memory size and approximation
quality. In section 4, a Q-learning based structure
optimized approach is developed. The proposed
approach is applied on the desired joint angel
tracking for biped robot in section 5. Conclusion and
further works are finally set out.
2 CMAC NN STRUCTURE AND
STRUCTURAL PARAMETERS
The output
Y
of the CMAC NN is computed using
two mappings. The first mapping
()
X
A projects
the input space point
12
[, , , ]
n
X
xx x  into a binary
associative vector
12
[, , , ]
C
N
A
aa a 
. Each element
of
A
is associated with one detector. When one
detector is activated, the corresponding element in
A
equals to 1, otherwise it equals to 0. The second
mapping
()
A
Y computes the output Y as a scalar
product of the association vector
A
and weight
vector
12
[, ,, ]
C
N
Www w 
according to relation (1),
where
()
T
X
represents the transpose of the input
vector.
()
T
YAXW
(1)
The weights of CMAC neural network are
updated by using equation (2).
()
i
wt and
1
()
i
wt

are
respectively the weights before and after training at
each sample time
i
t .
l
N is the generalization number
of each CMAC and

is a parameter included
in
[0 1] . e

is the error between the desired
output
d
Y of the CMAC and the computed
output
Y of the corresponding CMAC.
1
() ( )
ii
l
e
Wt Wt
N




(2)
Due to its structure, CMAC is preferable to be used
to approximate both linear and non-linear functions.
If the complexity of its structure is not increased
additionally, there are essentially two structural
factors ruling the function approximation quality.
The first one, called “quantization step”
q , allows
to map a continuous signal into a discrete signal.
The second parameter, called “generalization
parameter”
l
N , corresponds to the number of layers.
These two parameters allow to define the total
number of cells
C
N .
3 IMPACT OF STRUCTURAL
PARAMETERS ON CMAC NN
We try to show the relation between the structural
parameters of CMAC neural network, the quality of
the approximation and the required memory size for
a given function. Our study is based on an
experimental enquiry, in which several high-
dimension functions are used in order to test the
neural network’s approximation abilities. In this
section, take FSIN and two dimension GUASS
functions as examples, simulations for several step
quantization
q

are carried out, when the number of
layers increases from 5 to 50 for FSIN function, and
from 5 to 450 for two dimension GAUSS function.
For each of the aforementioned functions, a training
set including
100 100

random values, selected in
the corresponding two-dimensional space, has been
constructed. Weights of CMAC are updated using
equation (2). When CMAC is totally trained, three
modeling errors: mean absolute error
mean
E , mean
squared error
s
quare
E
and maximum absolute
error
max
E are carried out. The overview of the
obtained results for only three step quantization is
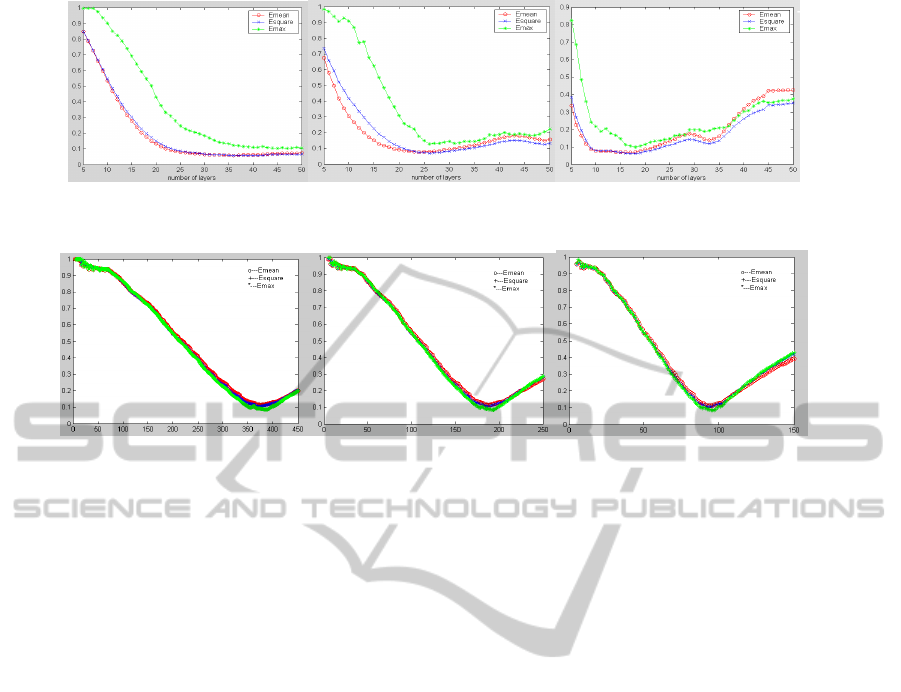
shown in Figure 1 and 2 respectively.
NCTA 2011 - International Conference on Neural Computation Theory and Applications
284

0.0025q 0.0050q

 0.0075q


Figure 1: Approximation error according to the number of layers for FSIN function with different step quantization.
0.0025q 0.0050q

 0.0100q


Figure 2: Approximation error according to number of layers for GUASS function with different step quantization.
When q is relatively small (for
example
0.0025q ), errors converges toward a
constant value close to the minimum error. But,
when the quantization is greater, results show there
is an optimal or near optimal structure when the
modeling errors can achieve minimum. However, it
must be noticed that for each quantization step, the
minimal errors are quasi-identical but for different
number of layers. As the curve trends of the mean
absolute error
mean
E , mean squared error
s
quare
E
and
maximum absolute error
max
E are same, only
take
s
quare
E as an example.
The mean squared error
s
quare
E for FSIN function
equals to 5.81% and 6.21% in the case
where
0.0025q and 0.0075q

 respectively.
These chosen results show that the approximation
abilities of the CMAC are similar in these two cases,
however, in the points of view of memory size,
for
0.0025q the required memory size is 4940,
3.5 times greater than when
0.0075q
(
1441
C
N  ). The experimental enquire simulation
results show that by optimizing CMAC structure, a
nearly minimal modeling error with much smaller
memory size can be achieved.
4 CMAC NN STRUCTURAL
PARAMETERS OPTIMIZATION
4.1 Structural Parameters Optimized
with Q-learning Approach
In this section, our goal is to design an optimizing
strategy allowing to adjust automatically the
structural parameters of CMAC NN in order to make
a tradeoff between the desirable approximation
quality and the limited memory size.
Q-Learning, proposed by Watkins (1992), is a
very interesting way to use reinforcement learning
strategy and is most advanced for which proofs of
convergence exist. It does not require the knowledge
of probability transitions from a state to another and
is model-free. Here, the Q-Learning based on the
temporal differences of order 0 is introduced, while
in our structure optimized approach only considering
the following step. Take the number of layers and
quantization step
[, ]
l
Nq

as two dimension states of
the world, while regarding the discrete actions as the
increment of these two scalars. There are four
possible actions when the agent searching the world:
1
2
3
4
1
1
lq
lq
l
l
aN q
aN q
aN q
aN q






















(3)
CMAC STRUCTURE OPTIMIZATION WITH Q-LEARNING APPROACH AND ITS APPLICATION
285

where
q

is the incremental quantity of quantization
step and the variation of layer is 1 for each step.
Change of the layer number and quantization step is
supposed to be alternated. Each discrete time step,
the agent observes state
[, ]
tt
l
Nq , take
action
tt
i
aA
(1,,4)i   , observes new
state
11
[, ]
tt
l
Nq

 , and receives immediate reward
t
r .
Transitions are probabilistic, that is,
11
[, ]
tt
l
Nq


and
t
r
are drawn from stationary
probability distributions. In our approach, Peseudo-
stochastic method is chosen to describe the
probability distributions.
The reinforcement signal
t
r provides information
in terms of reward or punishment. In our case, on
one hand, the reinforcement information has to take
into account the approximation quality of network.
On the other hand, the required memory size needs
to be minimized within the limitation. Taking these
considerations, we designed the reinforcement signal
as three cases:
·
1tt
s
quare square
EE


, the chosen of structural
parameters is towards the correct direction.
if
t
s
quare
E
and
t
C
N
achieve the desirable value
1
t
r

else
1
/ 1000 10(1 )
t
tt
C square
r
NE



(4)
·
1tt
s
quare square
EE

 , the trend of the chosen action is
not appropriate.
1
t
r


·
1tt
s
quare square
EE

 , appropriateness of the trends of
the chosen action is not clear.
0
t
r

In equation (4), factor 1000 and 10 are designed
only to balance the order of magnitude for memory
size and approximation quality.

indicates the
weight of these two structural parameters.
The Q matrix updates its evaluation of the value
of the action while taking in account the immediate
reinforcement
t
r and the estimated value of the new
state
11
(, )
tt t
l
VN q

 , that is defined by:
!
11 11
(, )max(, ,)
t
tt t t t
ll
bA
VN q QN q b

 

 
(5)
where
b is the action chosen within
1t
A

. If there is
enough learning, the update equation could be
written in the following form:
11
(, ,)(1 )(, ,)
[(,)]
ttt ttt
ll
tttt
l
QN qa QN qa
rVN q




 
 
(6)
where

is discount factor and

is the learning rate.
If there comes up the end of a period, there is not a
following state and the agent restarts a new sequence
of training. The updating equation is:
(, ,)(1 )(, ,)
ttt ttt t
ll
QN qa QN qa r



 
(7)
When the mean squared error satisfies the desirable
approximation (refers to equation (8)), and the
memory size is within the allocated rang as well
(presented in equation (9)), the goal state is
achieved.
td
s
quare square
EE
(8)
td
CC
NN
(9)
4.2 Simulation Results and
Convergence Analysis
Also, take FSIN function approximation as an
example. Suppose that the finite number of usable
memory size is 1500, and the approximation error
less than
6.00% is favorable in order to maintain the
approximation quality. In this case, we choose
6.00%
t
square
E  and 1500
t
C
N  as the goal state in
the training phase. The initial state of number of
layer
0
l
N
is set to be 20 and the quantization step can
be chosen randomly within
[0.0000 0.0100] , every
0.0002 as the incremental quantity
q

. In this
example, the discount factor

is set to be 0.9.
0 50 100 150 200 250 300 350 400
-40
-20
0
20
40
60
80
100
Episode
Sum r
Figure 3: Sum of ()Qt

for each episode.
Figure 3 shows the sum of the computing
value
()Qt

for each episode according to the
number of episode. This updating value, which
depends directly on the reinforcement signal,
converges toward 3 within 250 episodes. The
NCTA 2011 - International Conference on Neural Computation Theory and Applications
286

stability of our CMAC structure learning approach is
theoretically guaranteed by the proof of the Q-
learning convergence. After the training phase, the
CMAC with optimized structure
(
12
l
N  , 0.0084q ) can guarantee both of the
desirable approximation quality and limitation
required memory size, referring to Table 1.
Table 1: CMAC structure with minimum mean squared
error for FSIN function.
Structure Optimized
q
l
N
s
quare
E
C
N
NO 0.0025 41 5.81% 4940
YES 0.0084 12 5.94% 1431
5 THE APPLICATION OF CMAC
STRUCTURE OPTIMIZATION
In order to increase the robustness of control
strategy for robot, CMAC neural network has been
applied to learn a set of articular trajectories with
popularity. However, the CPU of the robot has to do
many intricacies tasks at the same time, therefore the
useable memory size is often allocated with
restriction or fixed number, and always the precise
control output is favorable. In this case, the
structural parameters optimization problem is
needed to be considered if we do not increase the
complexity of the CMAC NN, since the simplicity
of structure for network is always desirable. On the
basis of our previous work on the gait pattern
planning strategy of biped robot (C.Sabourin et al,
2008), CMAC structural parameters optimization
with Q-learning approach is applied to learn the joint
angle trajectories of biped robot.
Usually, after footstep planning strategy, the
position of the two stance feet can be calculated.
Therefore, it is not difficult to derive the trajectory
of the joint angle by inverse kinematics or bio-
inspired approach. The geometrical relationship
between stance leg and swing leg of biped robot is
described in Figure 4. Based on our control strategy,
each reference gait is characterized by both of the
step length and step height. Joint trajectory
associated to one gait is memorized into one CMAC
neural network. The biped robot is walking with a
weighted average of several reference trajectories.
Regarding the coordinate of swinging
foot
33
(, )
x
y
PP as the two inputs, two CMAC neural
networks are utilized for training hip joint angle
2

and knee joint angle
3

separately for each gait
pattern. The weights of CMAC are updated based on
the difference between the output of CMAC and
reference hip or knee joint angle of swinging leg.
33
(, )
xy
P
P
00
(, )
xy
P
P
12
ll
1
l
2
l
1

2

3

Figure 4: Geometrical relationship between stance leg and
swing leg.
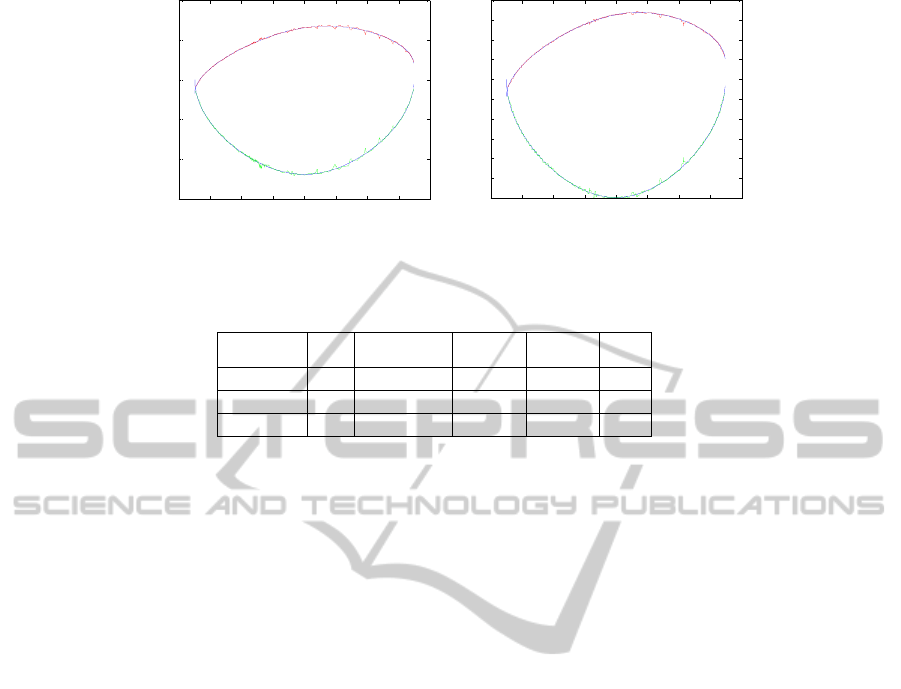
Figure 5 shows the results of swinging leg joint
angle approximation with CMAC, in which blue
curve stands for the reference joint angle profile, red
and green curves represent the output of CMAC
approximating hip and knee joint angle respectively.
In the first two simulations the structural parameters
are chosen randomly and we do not know if they are
appropriate. In the third experiment, the CMAC
structural parameters are learned based on the
developed Q-learning approach. We hope that the
approximation error of reference gait less
than
1.10% is better and the pre-assigned memory
size for each CMAC NN is 1000.
1.10%
d
square
E  and 1000
d
C
N  are set to be the goal
state according to equation (8) and (9),. After the
learning phase, the optimized parameters
are
20
l
N

,
12
0.0051qq

  (refers to
Figure5(b)). The required memory size and
approximation errors for both of the hip and knee
angles are listed in Table 2 for these three
experiments. In the first experiment, the calculated
mean squared error
(
2
1.16%
square
E


,
3
1.19%
square
E

 ) is very near to the
desirable value, but the utilized memory
size
3589
C
N

is 3.5 times bigger than the structure
optimized example. Since in this biped robot
application case, several reference pattern gaits have
to be stored, the total number of memory size
becomes quickly very large. In the second example,
the memory size is desirable, however, the
approximation quality of CMAC neural network
(
2
1.52%
square
E


,
3
1.56%
square
E

 ) is much worse
than the structure optimization case
(
2
1.07%
square
E

 ,
3
1.03%
square
E

 ). However, the
precise desired gait tracking is important in the case
of biped robot walking in the unknown environment.
CMAC STRUCTURE OPTIMIZATION WITH Q-LEARNING APPROACH AND ITS APPLICATION
287

-0.2 -0.15 -0.1 -0.05 0 0.05 0.1 0.15 0.2
-1.5
-1
-0.5
0
0.5
1
support leg joint angle profile
swinging leg joint angle profile
-0.2 -0.15 -0.1 -0.05 0 0.05 0.1 0.15 0.2
-1.2
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
support leg joint angle profile
swinging leg joint angle profile
(a) CMAC structure without learning (b) CMAC structure after learning
Figure 5: Joint trajectory tracking with CMAC Neural Network.
Table 2: Memory size and mean square error with randomly chosen and after learning CMAC structural parameters.
CMAC structure
l
N
12
qq


2
s
quare
E

3
s
quare
E

C
N
Randoml
y
chosen 30 0.0021 1.16% 1.19% 3598
Randoml
y
chosen 10 0.0080 1.56% 1.52% 795
After learnin
g
20 0.0051 1.07% 1.03% 993
6 CONCLUSIONS
Besides the appealing advantages of CMAC NN,
such as simple and effective training properties and
fast learning convergence, a crucial problem to
design CMAC is related to the choice of the neural
network’s structural parameters. In this paper, we
have shown how both the number of layers and step
quantization influence the approximation qualities of
CMAC neural networks. The presented simulation
results show that by optimizing CMAC structure, a
nearly minimal modeling error with much smaller
memory size can be achieved. Consequently, a
CMAC structure optimization approach which is
based on Q-learning is proposed. The stability of our
proposed approach is theoretically guaranteed by the
proof of the learning convergence of Q-learning.
This Q-learning based structure optimization method
is applied on generating the joint angle of biped
robot.
Simulation results show that the choice of an
adaptive structure of CMAC allows on one hand
decreasing the memory size and on the other hand
achieving the desirable approximation quality.
ACKNOWLEDGEMENTS
This research is supported by the fundamental
research fund of Northwestern Polytechnical
University (JC20100211), P.R.China.
REFERENCES
J. S. Albus, 1975. A new approach to manipulator control:
The cerebellar model articulation controller (CMAC).
Transactions of the ASME: Journal of Dynamic
Systems, Measurement, and Control
, 9:220-227.
Hung-Ching Lu, Ming-Feng Yeh, Jui-Chi Chang, 2006.
CMAC study with adaptive quantization.
IEEE Int.
Conf. on Systems, Man, and Cybernetics
, pp.2596-
2601.
S. D. Teddy, E. M.-K. Lai, C. Quek, 2007. Hierarchically
clustered adaptive quantization CMAC and its
learning convergence.
IEEE Trans. on Neural
Networks
, 18(6):1658-1682.
A. Menozzi, M. Chow, 1997. On the training of a multi-
resolution CMAC neural network.
Proc. Int. Conf.
Ind. Electron. Control Instrum.
3:1130–1135.
Chih-Min Lin, Te-Yu Chen, 2009. Self-organizing CMAC
control for a class of MIMO uncertain nonlinear
systems.
IEEE Trans. on Neural Networks,
20(9):1377-1384.
M. N. Nguyen, D. Shi, C. Quek, 2005. Self-organizing
Gaussian fuzzy CMAC with truth value restriction.
Proc. IEEE ICITA, pp.185–190, Sydney, Australia.
Daming Shi, Minh Nhut Nguyen, Suiping Zhou, Guisheng
Yin, 2010. Fuzzy CMAC with incremental Bayesian
Ying-Yang learning and dynamic rule construction,
IEEE Trans. on Systems, Man and Cybernetics,
40(2):548-552.
C. Watkins, P. Dayan, 1992. Q-learning.
Machine
Learning
, 8:279–292.
C. Sabourin, K. Madani, Weiwei Yu, Jie Yan, 2008.
Obstacle Avoidance Strategy for Biped Robot Based
on Fuzzy Q-Learning Approach, International
Conference on Automatic Control & Robotics,
Portugal.
NCTA 2011 - International Conference on Neural Computation Theory and Applications
288