
FINDING PATHS CONNECTING TWO PROPER NOUNS USING
AN ANT COLONY ALGORITHM
Dinesh Hakande
Birla Institute of Technology, Mesra, Ranchi, India
Keywords: Freebase, Relevant, Ant colony optimization, Wiki mining, Web 2.0.
Abstract: Collaborative systems available on the Web allow millions of users to share information through a growing
collection of tools and platforms such as wiki- patforms, blogs, and shared forums. With abundant
information resources on the Internet such as Wikipedia or the Freebase, we study the connections between
two proper nouns. Nevertheless, the problem is a challenging search problem, as information on the Internet
is undoubtedly large and full of irrelevant information. In this project, we first parse and mine the entire
Freebase database in order to extract the relevant information of proper nouns. Further we apply Ant Colony
Optimization method for finding the path that connects two proper nouns together.
1 INTRODUCTION
This paper is on idea that we can connect any two
random people in the world. We wonder whether
there is any similarity for the pair of proper nouns in
the real world knowledge base. Here, we are
interested in using data obtained from the Internet to
uncover hidden connections between two proper
nouns in interesting ways. The goal of the project is
to come up with an algorithm and a set of heuristics
that would make the search most efficient but at the
same time yield interesting results.
Specifically, our program takes as inputs two
proper nouns in natural language and the number of
paths connecting the two proper nouns the user
wants to search for. Then, to resolve the ambiguity
between objects sharing the same name, the program
prints out a short description of each of the objects
and asks the user to choose which of the objects she
is actually interested in. Subsequently, the program
starts running a pre-chosen search algorithm with
pre-chosen heuristics to determine a path between
the two objects. A path is defined to be a series of
objects that connect to each other via some type of
relationship, starting from the start object and ending
the goal object. The connection between two nodes
has a semantically relationship, elucidated in
"capital city of", "sent delegates to", or "was held
in", as its value. The program belches out paths
connecting the two objects and the relationship types
of all the objects along the paths. Here, we use the
concept of “Ant Colony Optimization” for finding
the path that connects two proper nouns together.
Ant colony optimization algorithm (ACO) is a
probabilistic technique for solving computational
problems which can be reduced to finding more
suited paths using graphs. In real world, ants are
capable of finding the shortest path from a food
source to the colony without using visual cues. Also,
their routed ways are amenable to changes in the
immediate environment, for example finding a new
shortest path once the old one is no longer feasible
due to an impending obstacle. It is well known that
the primary means for ants to form and maintain
their line of supply is creating a pheromone trail.
Ants release measured quantities of pheromone
while walking, and each ant probabilistically prefers
to follow a direction rich in pheromone. This
elementary behavior of real ants can be used to
correlate to find the paths that connect two nouns
together. The project is interesting in two ways.
First, it could be a fun, interactive game or tool. We
believe that there are often some unknown but
interesting relationships that two objects have in
common. For example, not many people at Harvard
know that both Harvard University and the
California's Great America theme park in San
Francisco are of the same total land area. The well-
known personalities George Washington and
Edward Kennedy were born on February 22
nd
as,
also the well known physicists Galileo Galilei and
346
Hakande D..
FINDING PATHS CONNECTING TWO PROPER NOUNS USING AN ANT COLONY ALGORITHM.
DOI: 10.5220/0003694703460351
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2011), pages 346-351
ISBN: 978-989-8425-83-6
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

Stephen Hawking were both born on January 8
th
.
Second, the project could be used as part of a system
for related topic discovery. By using the proposed
program, we can tell whether two random words are
related enough using some aggregating function,
such as the average length of the paths between the
two objects. It is possible to use a similar system
through this project to recommend related topics the
user might be interested in, while he is browsing on
a webpage.
In addition to finding the project interesting, we
also think that the problem space of the project is
computationally challenging. First, we are doing
search on a real world, half-user-generated and half-
regulated data, which means that our search problem
could be very large and full of irrelevant
information. Branching factor is an issue in our
search space, as each node can connect to thousands
of other nodes. Besides, as we solicit data in real-
time, expanding a node is very costly. Finally, with
online, real-world data, there are many information-
based and graph-based heuristics we can use.
Information-based heuristics are those that involve
understanding the nature of the actual content,
whereas graph-based heuristics are those that infer
some information about each of the nodes through
the structure of the graph.
The rest of the paper is organized as follows:
In Section 2, we explain related works and our
research into the problem space. Section 3 explains
the method used to implement the project and the
basic algorithms we implemented in the project.
Future works is mentioned in Section 5.
2 BACKGROUND
2.1 Related Work
There are many existing online systems that involve
representing data using nodes and infer implicit
information through the connections between those
nodes and the structure of the resulted graph. A
Facebook platform application named "Six Degrees"
was developed by Karl Bunyan, which calculates the
degrees of separation between different people. Six
Degrees of Separation is the idea that any two
random people in the world are at most six degrees
apart in terms of social connections from each other.
Also, Google's PageRank algorithm uses the graph
structure to represent the connections between
websites, and assumes that nodes with many
incoming links are interesting and trustworthy.
Nevertheless, we have not seen any system similar
to ours, which attempts to find connections between
any two proper nouns through ant search
optimization.
2.2 Wikipedia and Natural Language
Processor
Originally, we planned to use Wikipedia as our
source of data, as it is an arguably richest free source
of information on the Internet. Our plan of action
was to scrape a respective Wikipedia page and then
use an open-source natural language processor to try
to understand the sentence structure. However, we
decided to not use this approach due to various
reasons as explained in Section 2.3.
2.3 Freebase
Freebase is a large collaborative knowledge base
consisting of metadata composed mainly by its
community members. It is an online collection of
structured data harvested from many sources,
including individual 'wiki' contributions. Freebase
treats all articles as nodes, and nodes can connect to
each other via some descriptive links. For instance,
the node /en/coldplay, which represents the English
band Coldplay, connects to the node /guid/
9202a8c04000641f800000000839684a, which re-
presents the song Viva la Vida, via the link
/music/track/recorded_by, which represents "re-
corded by." Freebase API queries can be done via
HTTP using Freebase specific Metaweb Query
Language (MQL), which resembles JSON. We
decided to opt for Freebase instead of Wikipedia due
to many reasons.
First, no natural language processors will be
good enough for us to extract the relationship
between two objects the way Freebase provides us,
meaning that using Wikipedia, we might not be able
to make sense of the path we find. Second, since
everything on Freebase is an object, it provides us a
much easier way to deal with ambiguity between
objects of the same name than using a natural
language processor. Lastly, we believe that a
Freebase query is much faster than running a natural
language processor on a scraped Wikipedia page
3 METHOD AND ALGORITHM
3.1 Freebase
Everything on Freebase, including articles,
community portals, links, images, properties, user
FINDING PATHS CONNECTING TWO PROPER NOUNS USING AN ANT COLONY ALGORITHM
347

data, and Freebase's internal properties, is
represented as a node. Each node has a type
property, which lets us know which type(s) that
particular node belongs to. We do basic pruning
when we first obtain data in order to get rid of
irrelevant nodes, such as images, community portals,
Freebase's user information, and Freebase's internal
properties. Nevertheless, many nodes, such as
country nodes, still have more than a thousand of
connections left. Thus, we use a series of heuristics
to cut down the number of nodes to be passed into
the search algorithm. First, when we get all the
neighbors of a node, we scan through all the
"relationship type", and downplay the relationship
types that are too abundant. For example, the
relationship type /location/location/contains has
more than 1,000 connections for United States,
implying that this relationship type is likely to not be
very important (as opposed to the relationship type
/location/country/capitals, which contains only 1
connection
3.2 Artificial Ants
In this work an artificial ant is an agent which moves
from information
1
to information on a heuristic
graph. With each information we assign randomly
attractive_value based on user’s Interestingness.
Interestingness means how interesting the paths are.
It chooses the attractiveness
2
of information using a
probabilistic function both of a trail accumulated on
edges and of a heuristic value, which was chosen
here to be a function of the edge attractiveness.
Artificial ants probabilistically prefer information
that are connected by edges with a lot of pheromone
trail and which are close-by. Initially, m artificial
ants are placed on randomly selected information. At
each time step they move to new information and
modify the pheromone trail on the edges used –this
is termed local trail updating. When all the ants
have completed a tour the ant that has made the
shortest tour modifies the edges belonging to its tour
–termed as global trail updating– by adding an
amount of pheromone trail that is inversely
proportional to the attractive_value of information.
Artificial ants can determine how attractive the
information are, and they are endowed with a
working memory M
k
used to memorize information
already visited (the working memory is emptied at
the beginning of each new tour, and is updated after
1
Information may be defined as a set of data values that
is extracted from freebase database.
2
Attractiveness is the measure of attractive_value
each time step by adding the new visited city).
In our ant colony system (ACS) an artificial ant k
of information r chooses the information s to move
to among those which do not belong to its working
memory M
k
by applying the following probabilistic
formula(1):
s =
arg max{ [
τ(
r,u)] [
η(
r,u)
β
]
}
if q <
q
0
(1)
S otherwise
where τ(r,u) is the amount of pheromone trail on
edge (r,u). η(r,u) is a heuristic function, which was
chosen to be the inverse of the attractive_value of
information between database r and u, β is a
parameter which weighs the relative importance of
pheromone trail and of closeness, q is a value chosen
randomly with uniform probability in [0,1], q
0
is a
parameter, and S is a random variable selected
according to the following probability distribution,
which favors edges which are shorter and have a
higher level of pheromone trail
:
p
k
(r,s) =
[
τ(
r,s
)
] [
η(
r,s
)
]
β
∑ [τ(r,u)] [η(r,u)]
β
uɆM
k
if s Ɇ M
k
(2)
0 otherwise
where p
k
(r,s) is the probability with which ant k
chooses to move from information r to information
s. Pheromone trail is changed both locally and
globally. Global updating is intended to reward
edges belonging to shorter tours. Once artificial ants
have completed their tours, the best ant deposits
pheromone on visited edges; that is, on those edges
that belong to its tour. (The other edges remain
unchanged.) The amount of pheromone Δϕ(r,
s) deposited on each visited edge (r,s) by the best ant
is inversely proportional to the sum of all
attractive_value in a tour: Minimum the
attractive_value greater the amount of pheromone
deposited on edges and is shortest_route. This
manner of depositing pheromone is intended to
emulate the property of differential pheromone trail
accumulation, which in the case of real ants was due
to the interplay between length of the path and
continuity of time. The global trail updating formula
is
ϕ(r, s) (1-α )∗ϕ(r, s) +α ∗ ϕ(r, s)
where ϕ(r, s)=(shortest_tour)-1. Global trail
updating is similar to a reinforcement learning
scheme
in which better solutions get a higher
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
348

reinforcement.
Local updating is intended to avoid a very strong
edge being chosen by all the ants: Every time an
edge is chosen by an ant its amount of pheromone is
changed by applying the local trail updating
formula
:
τ(r, s) (1-α )∗τ(r, s) +α ∗ τ
0
where t
0
is a parameter. Local trail updating is also
motivated by trail evaporation in real ants.
Interestingly, we can interpret the ant colony as a
reinforcement learning system, in which
reinforcements modify the strength (i.e., pheromone
trail) of connections between proper nouns. In fact,
the above formulas (1) and (2) dictate that an ant can
either, with probability q
0
, exploit the experience
accumulated by the ant colony in the form of
pheromone trail (pheromone trail will tend to grow
on those edges which belong to short tours, making
them more desirable), or with probability (1- q
0
),
apply a biased exploration (exploration is biased
towards short and high trail edges) of new paths by
choosing the information to move to randomly, with
a probability distribution that is a function of both
the accumulated pheromone trail, the heuristic
function, and the working memory M
k
.
3.3 Algorithm
1. Assign attractive_value to the information
2. Read two proper nouns
// Set initial Pheromone detail
3. for every edge(i,j) do
τ
ij
:= τ
0
End for
4. fork:=1 to m (m=number of ants) do
Each ant is individually placed on initial
state with empty memory
.
End For
5. for k:=1 to m do
Ant chooses the next information s with the
probability
[τ(r,s)] [η(r,s)]
β
p
k
(r,s) :=
∑ [τ(r,u)] [η(r,u)]
β
uɆM
k
where r is the current information
End for
6. for every edge(i,j) do
Update local trials by the formula
τ(r, s) (1-α )∗τ(r, s) +α ∗ τ
0
and the global trial by the formula
ϕ(r, s) (1-α )∗ϕ(r, s) +α ∗ ϕ(r, s)
End for
7. for k:=1to m do
If an attractive information is found then
Update the path
End If
End for
8. print path between two noun and attractive
information
9. STOP
4 EXPERIMENT AND RESULT
Experiments are performed to check the
performance of the Ant Colony Optimization to find
path between two proper nouns.
The parameters
were set to the following values: β=2, α=0.1,
τ
0
=(n·L
nn
)
-1
, where L
nn
is the total path produced by
the nearest neighbor heuristic based on
attractive_value , and n is the number of information
(these values were found to be very robust across a
wide variety of problems). We initially look at this
problem with 60 nodes of information (N=60). Let
(x
n
,y
n
) be the co-ordinates of n
th
node visited. With
60 nodes of information, 6027 paths were covered at
about 15 second by Ant Colony Optimization
method.
Figure 1: Result by Ant Colony Optimization.
The entities are discussed as follows:
0 1 2 3 4 5 6 7 8
0 2 4 6 8
10
Random Locations of inforation
Attractiveness M atrix
5 10 15 20 25 30 35 40
1020304050
0 1 2 3 4 5 6 7 8
0 2 4 6 8
10
Total nodes of information = 57.2928
FINDING PATHS CONNECTING TWO PROPER NOUNS USING AN ANT COLONY ALGORITHM
349
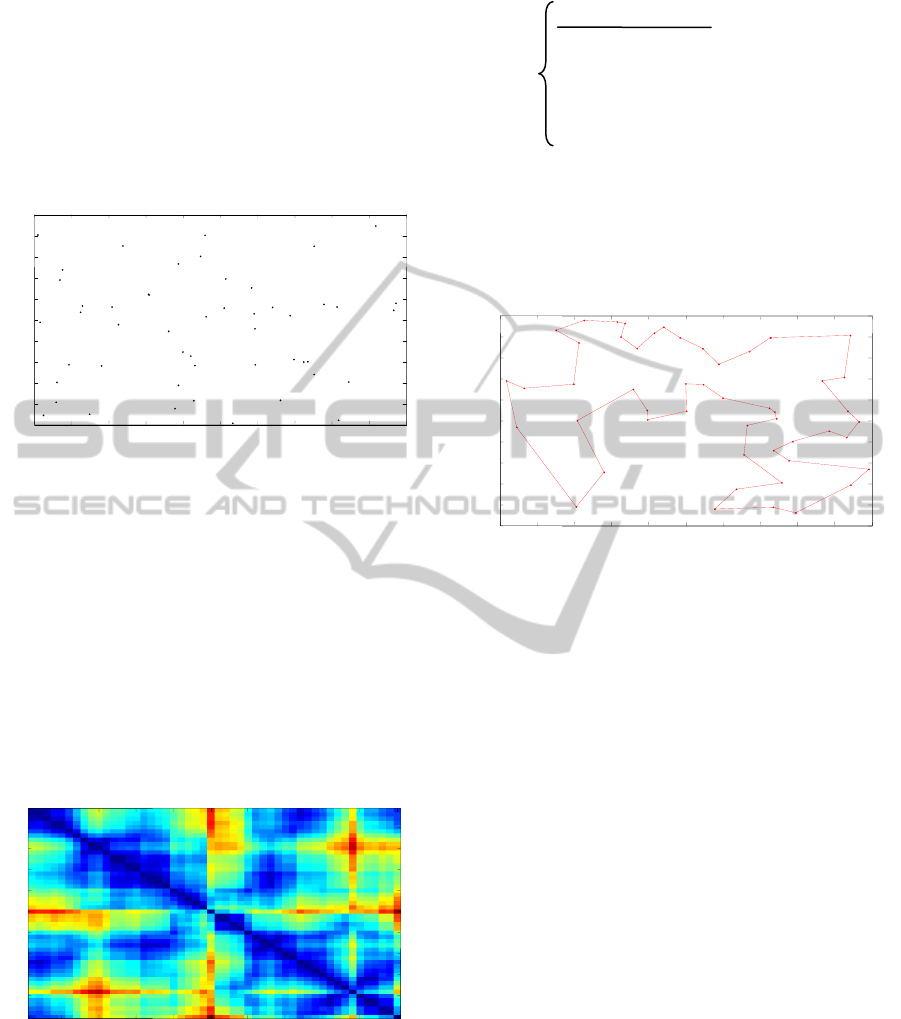
4.1 Random Location of Information
First of all one of the most important issue is how
are we going to access information, where
information is a set of data values that is extracted
from freebase database. We do so by placing an ant
randomly at each of the available information as
shown in figure 1.
Figure 2: Random Location of Information.
4.2 Attractiveness Matrix
As discussed in section 3.2, attractiveness is the
measure of attractive_value. With each of this
information we assign attractive_value, as shown in
figure 2, based on user’s interestingness we create an
attractiveness matrix, which is beneficial for ants to
complete their path in order to search for new
interesting information. Here we put starting and
ending location of nodes such that (x
0
,y
0
) =
(x
N+1
,y
N+1
).
Figure 3: Attractiveness Matrix of the information
4.3 Completion of Path
As discussed in section 3.2, an ant k of information
r chooses the information s to complete its path by
the probabilistic formula
p
k
(r,s) =
[
τ(
r,s
)
] [
η(
r,s
)
]
β
∑ [τ(r,u)] [η(r,u)]
β
uɆM
k
if s Ɇ M
k
0 otherwise
Local trail Updating and global trial updating
was done in order to get optimized path, and the
result obtained is shown in figure 3.
Here β is chosen as 2 and τ
0
as (n L
nn
)
-1
.Result
obtained is shown in figure 3.
Figure 4: Total Nodes of Information.
5 FUTURE WORKS
In the future, we would like to bring our application
online where people can use it freely to search
whatever things they like. Before that, we need to do
several things. We need to conduct more evaluations
to figure out semantics of certain parameters. We
need to improve memory usage so that it can handle
multiple tasks at the same time and also we may try
scraping Wikipedia instead of Freebase in the future.
There are many ways in which Ant colony
algorithm can be improved so that the unnecessary
extra numerary paths needed to reach a comparable
performance level can be diminished, making its
application to larger problem-instances feasible.
First, a local optimization heuristic like 2-opt, 3-opt
or Lin-Kernighan (Linand Kernighan, 1973) can be
embedded in the Ant colony algorithm (this is a
standard approach to improve efficiency of general
purpose algorithms. In the experiments presented in
this article, local optimization was just used to
improve on the best results produced by the various
algorithms. On the contrary, each ant could be taken
to its local optimum before global trail updating is
performed. Second, the algorithm is amenable to
0
1 2 3 4 5 6 7 8 9
0
1 2 3 4 5 6 7 8 9
10
Total nodes of information = 61.2344
x- abscissa of the visited node by Ant Colony
Optimazation
x
5 10 15 20 25 30 35 40 45
5
1015202530354045
50
0
1 2 3 4 5 6 7 8 9
0
1 2 3 4 5 6 7 8 9
10
Random Locations of inforation
X
y-ordinate of random location of
information
Total nodes of information = 61.2344
Attractive_value
y-ordinate of visited nodes by
Ant Colon
y
O
p
timization
ECTA 2011 - International Conference on Evolutionary Computation Theory and Applications
350

efficient parallelization, which could greatly
improve the performance for finding good solutions,
especially for high-dimensional problems. The most
immediate parallelization of Ant colony algorithm
can be achieved by distributing ants on different
processors: the same algorithm is then solved on
each processor by a smaller number of ants, and the
best tour found hence is exchanged asynchronously
among processors. A preliminary implementation on
a net of transputers has shown that it can make the
complexity of the algorithm largely independent of
the number of ants. Third, the method is open to
further improvements such as the introduction of
specialized families of ants, tighter connections with
reinforcement learning methods, and the introduc-
tion of more specialized heuristic functions to direct
the search.
6 CONCLUSIONS
We implemented the application, with ant colony
algorithm. The key to the application of Ant colony
algorithm to a new problem is to identify an
appropriate representation for the new problem (to
be represented as a graph searched by many artificial
ants), and an appropriate heuristic that defines the
attractiveness between any two nodes of the graph.
Then the probabilistic interaction among the
artificial ants mediated by the pheromone trail
deposited on the graph edges will generate good, and
often optimal, problem solutions
.
REFERENCES
Dorigo, M. (1992) "Optimization, Learning and Natural
Algorithms", PhD Thesis, Dipartimento di Elettronica,
Politechico di Milano, Italy.
Dorigo, M. and Gambardella, L. (1997) "Ant Colony
System: A Cooperative Learning Approach to the
Traveling Salesman Problem", IEEE Transactions on
Evolutionary Computing, 1, pp. 53-66.
A N Langville, C D Meyer and P FernÁndez. Google’s
pagerank and beyond: The science of Search engine
rankings. The Mathematic Intelligencer, 30(1), 2008.
E Friedman, P Resnick, and R Sami. Manipulation-
resistant Reputation systems. Algorithmic Game
Theory, 2007
Freebase, http://www.freebase.com
H. Fan, Z. Hua, J. Li, D. Yuan, “Solving a shortest a path
problem by ant algorithm”, Proceedings of the Third
International Conference on Machine Learning and
Cybernetics, Shanghai, 26-29 August 2004.
C. Chu, J. Gu, X. Hou, Q. Gu, “A heuristic ant algorithm
for solving QoS multicast routing problem”, IEEE
2002.
M. Dorigo, G. Di Caro, and L.M. Gambardella,“Ant
algorithm for discrete optimization”, Artificial Life,
vol. 5, no. 2, pp. 137-172, 1999.
M. Dorigo, Ant colony optimization web page, http://
iridia.ulb.ac.be/mdorigo/ACO/ACO.htm
FINDING PATHS CONNECTING TWO PROPER NOUNS USING AN ANT COLONY ALGORITHM
351
