MAPPING KNOWLEDGE DOMAINS

Combining Symbolic Relations with Graph Theory

Eric SanJuan

LIA, University of Avignon, 339 Chemin des Meinajaries, Avignon, France

Keywords: Terminology, Multi word terms, Graph decomposition, Maximal clique separators, Formal concept analysis.

Abstract: We present a symbolic and graph-based approach for mapping knowledge domains. The symbolic

component relies on shallow linguistic processing of texts to extract multi-word terms and cluster them

based on lexico-syntactic relations. The clusters are subjected to graph decomposition basing on inherent

graph theoretic properties of association graphs of items (authors-terms, documents-authors, etc). These

include the search for complete minimal separators that can decompose the graphs into central (core topics)

and peripheral atoms. The methodology is implemented in the TermWatch system and can be used for

several text mining tasks. We also mined for frequent itemsets as a means of revealing dependencies

between formal concepts in the corpus. A comparison of the frequent itemsets extracted on each dataset and

the structure of the central atom shows an interesting overlap. The interesting features of our approach lie in

the combination of state-of-the-art techniques from Natural Language Processing (NLP), Clustering and

Graph Theory to develop a system and methodology adapted to uncovering hidden sub-structures from

texts.

1 INTRODUCTION

A timely awareness of recent trends in scientific

domains is necessary to support several information

intensive activities such as innovation, science and

technology watch, business intelligence to name

only a few. Such studies are usually conducted by

analyzing the electronic literature available on line

based on different approaches such as citation

analysis, text and document clustering, pattern

mining, novelty detection. Bibliometrics aims to

elaborate indicators of the evolution of scientific

activities using statistical and mathematical models.

The two major bibliometric methods are co-citation

and co-word analyses. Co-citation analysis has

proved useful in highlighting major actors in a field

(the "who's who" of a field). Although some

attempts have been made to work directly at the text

level in bibliometrics, natural language processing

(NLP) resources and capabilities have barely been

tapped by this community. The most common NLP

processing is limited to stemming prior to clustering

(Prize and Thelwal, 2005). Text units have mainly

been considered either as a bag-of-words or as a

sequence of n-grams in the vast majority of topic

mapping systems.

We take a different approach to text clustering

and consider that a multi-disciplinary effort

integrating surface linguistic techniques is necessary

to elaborate indicators of topics trends at the level of

texts. For this, we require a more fine-grained

analysis, involving prior linguistic processing of the

scientific literatures before applying statistical and

mathematical models. The interesting features of our

approach lie in the combination of state-of-the-art

techniques from three disciplines: Natural Language

Processing (NLP), Clustering and Graph Theory.

NLP enables us to extract meaningful textual units

and identify relevant information between them,

here multi-word terminological units. These text

chunks correspond to domain concepts and the

linguistic relations are lexical, syntactic and

semantic variations. These variations are used in

later stages of processing (clustering) to form topics

through relations of synonymy and

hyponymy/hypernymy and semantic relatedness.

Prior grouping of term variants ensures that

semantically close terms which reflect different

aspects of the same topic are certain to end up in the

same cluster at the end of the process. The linguistic

theory behind the grouping of terms either by shared

modifiers or by shared head is known as

527

SanJuan E..

MAPPING KNOWLEDGE DOMAINS - Combining Symbolic Relations with Graph Theory.

DOI: 10.5220/0003721105190528

In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (SSTM-2011), pages 519-528

ISBN: 978-989-8425-79-9

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

distributional analysis and was introduced by Harris

(1966). It was later taken up by various studies in

automatic thesaurus construction (Grefenstette,

1997); (Wacholder, 2001). We extended the

definition of the types of relations identified and

added additional constraints like the position of

added words and their number to avoid generating

spurious variants (Ibekwe-SanJuan, 1998). Co-

occurrence (numerical) is optionally added during

clustering as a means to capture the supplementary

dimension of interactions between domain concepts.

The end results are clusters of high semantic

homogeneity which also capture the most salient

association links. This way of building clusters by

first grouping semantic variants of the same terms,

then by gradually incorporating significant

associated concepts based on co-occurrence

constitutes is unique to the best of our knowledge.

We designed a hierarchical clustering algorithm

to suit the characteristics of our input units (multi-

word terms). This algorithm clusters the multi-word

terms grouped into close semantic classes called

components using optionally co-occurrence

information. The clusters are represented as an

undirected graph. This graph is further subjected to a

graph decomposition algorithm which splits

complex terminological networks of topics based on

their graph theoretic properties in order to identify

sub-structures that represent highly connected sets of

topics called central atom and distinct sets topics

called peripheral atoms).

Our system, TermWatch is adapted to mapping

knowledge domains at the micro level. Different

stages of the overall methodology have been

described in previous publications (SanJuan and

Ibekwe-SanJuan, 2006). The system has been

applied successfully to text corpora from different

domains and on several knowledge intensive tasks

such as knowledge domain mapping in information

retrieval ontology population in the biomedical

domain (SanJuan et al. 2005), opinion categorization

of literature reviews (Chen et al. 2006). The recent

enhancement to the system is the graph

decomposition algorithm which enables the system

to decompose complex graphs into more legible

subgraphs representing coherent networks of

research topics.

This paper is divided into three main sections.

First a general description of TermWatch section 1,

followed in section 2 by the terminological graph

extraction process and decomposition. Finally, we

present in section 3 a short summary of one case

study.

2 TERMWATCH OVERVIEW

TermWatch (http://termwatch.es) is designed to map

research topics from unstructured texts and track

their evolution in time. The system combines

linguistic relations with co-occurrence information

in order to capture all possible dimensions of the

relations between domain concepts. The processing

of texts relies on surface linguistic relations between

multi-word terms (MWTs) to build semantically

tight clusters of topics. The processes leading from

the input of a raw texts to the mapping of domain

topics can be broken down into five major stages:

multi-word term extraction, term variants

identification, term clustering, graph decomposition

and visualization. Figure 1 shows the overall

process. As some components of the system have

been described in previous publications (SanJuan

and Ibekwe-SanJuan, 2004; 2006), we will focus

particularly on the graph decomposition algorithm of

terminological graphs which aims to reveal a family

of formal concepts and their relationships. A step-

by-step procedure going from input texts to topic

mapping consists in the following:

1. Build a scientific corpus reflecting a research

question. The input corpus is composed of raw texts.

2. Terminological noun phrases (NPs) of maximal

length are extracted using TreeTagger (Schmid

1999) or any POS tagger. A selection of NPs is done

based on their syntactic structure and on our

enhanced term weighting function in order to retain

only domain terms.

3. Terms that are semantic variants of one another

are detected and clustered in a hierarchical process.

This results in a three level structuring of domain

terms. The first level are the terms. The second level

are components that group together terms

semantically close terms or synonyms. Roughly,

TermWatch's components generalize the notion of

WordNet synsets to multi-word terms. A clustering

algorithm is applied to this second level of term

grouping based on a weighted graph of term

variants. Components and clusters are labeled by

their most active term and can be used as document

features.

4. In the fourth stage, documents are indexed by

cluster or component labels and the corresponding

association graph is generated. The strength of the

association is weighted based on different similarity

measures and only those links that are above some

threshold for all measures are considered.

5. Association graphs are decomposed into atoms.

An atom is a subgraph without clique separators.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

528

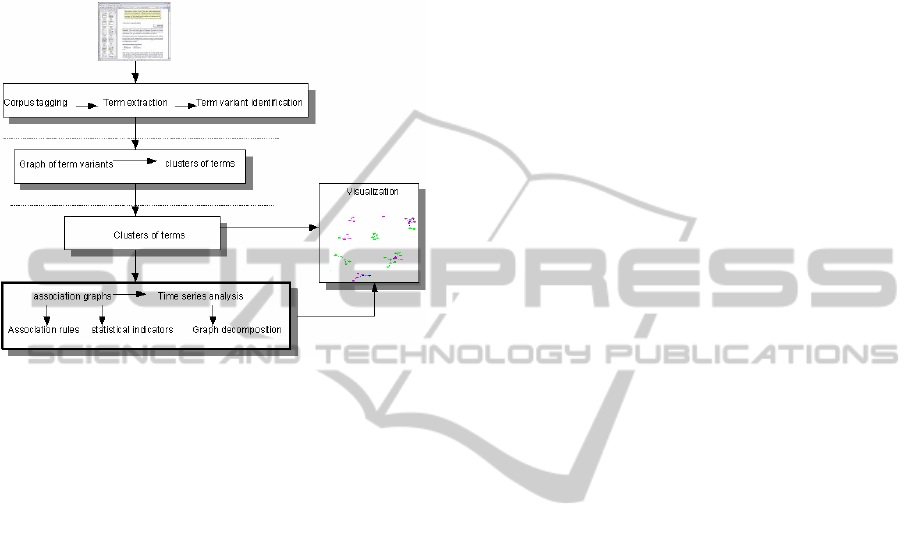
Each clique corresponds to a formal concept. Major

atoms are detected and visualized using force

directed placement algorithms. The periphery of big

atoms is highlighted since it can reveal new concepts

arising in a domain represented by a central more

bigger atom.

Figure 1: Overview of the mapping knowledge domains

process in TermWatch.

3 TERMINOLOGICAL GRAPH

EXTRACTION

3.1 Term Extraction

After the corpus has been tagged using TreeTagger

(Schmid, 1999), contextual rules are used to extract

multi-word terms based on morphological and

syntactic properties of terms. One such rule is the

following:

<mod>* <N>+

then return:

1) <mod>* <N>+ of <mod>* <N>+

2) <mod>* <N>+

where:

<mod> = a determiner and/or an adjective

<N> = any of the noun tags

<prep1> = all the prepositions excluding ‘‘of’’

* = Kleene’s operator (zero or n occurrences of an

item)

+ = at least one occurrence

This rule favors the extraction of terminological

noun phrases in a preposition structure where the

preposition is “of”. This preposition has been found

to play an active role in the multi-word term

formation process. More details of the rules can be

found in (SanJuan and Ibekwe-SanJuan, 2006). The

extracted terms can be simplex noun phrases (NPs)

like “stress disorder” or complex ones like

“posttraumatic stress disorder” which embeds

simpler NPs. Also, terms are extracted in their two

possible syntactic structures: NPs with prepositional

attachment (execution of innocent victims) and

compounds (innocent victims execution). This

transformation operation, also known as permutation

is useful for grouping together syntactic variants of

the same concept that would otherwise be dispersed.

No limit is imposed on the length of the extracted

terms thus ensuring that new terms coined by

authors of papers are extracted 'as is' and that

existing domain concepts with multi-words are not

altered or lost. By not resorting to the usual “bag-of-

word” approach common in the IR and data mining

communities, emergent domain terms can be

identified in a timely manner because term

extraction respects the structure of the domain

terminology “in-the-making”.

3.2 Generating a Graph of Semantic

Term Variants

We studied linguistic operations between terms

which are domain independent and can be used to

build taxonomies, thesaurus or ontologies. These

operations, called terminological variations, stem

from two main linguistic operations: lexical

inclusion and lexical substitution. By lexical

inclusion, we refer to the case where a shorter term

is embedded in a longer one through three specific

operations: insertions (severe poisoning - severe

food poisoning), modifier or head word expansion

(disaster intervention - disaster intervention call). By

lexical substitution, we refer to the case where terms

of identical length share a subset of lexical items

save one in the same position (political violence

threat - political violence campaign). Lexical

inclusion often engenders hypernym/hyponym

(generic/specific) relations between terms while the

lexical substitution tend to indicate a loose kind of

semantic association between terms. Lexical

substitutions between binary terms give rise to a

highly connected graph of term variants (cliques)

which may include some amount of noise (spurious

relations). They are filtered using two criteria: we

retain only those substitutions that involve terms of

length >2, if the words in the same grammatical

position are found in the same WordNet synset.

Although there are many more types of linguistic

relations, we restricted our choice to those that did

MAPPING KNOWLEDGE DOMAINS - Combining Symbolic Relations with Graph Theory

529

not require heavy use of external semantic resources

and were domain-independent, thus found in any

well written text revolving around the same broad

topic.

We also acquired explicit synonymy links

between multi-word terms using WordNet. To do

this, we extended the single word-word relations in

WordNet to multi-word terms by adding these

restrictions: two multi-word terms are considered to

be in a synonymy relation if two of their words are

in the same WordNet synset, occupy the same

grammatical role in the terms (both head words or

modifier words) and are found in the same position.

The table below shows some of the synonyms

identified in this way. The italicized words were in

the same WordNet synset.

Table 1 shows that the quality of the synonyms

acquired through WordNet is indeed good. Table 2

gives examples of the different relations identified

and the number of terms involved in a corpus

dealing with terrorism. This corpus was built

following a search on the WoS using the word

“terrorism”. 3,366 bibliographic records were

collected on what researchers have been writing

about terrorism. Previous studies have sought to map

the terrorism domain either from this same

perspective (Chen, 2006) or from that of groups

actively involved in plotting and carrying out

terrorist acts (Chen et al., 2008). Of particular

relevance to our study is the one done by Chen

(2006). This author used the same database and the

same query but on an earlier and shorter period

(1990-2003).

Table 1: Some synonyms acquired from the terrorism

corpus using WordNet synsets.

Term Synonym identified using

WordNet synsets

september 11 wake september 11 aftermath

united states federal

agency

united states federal bureau

risk society conception risk society concept

Trauma type injury type

Life-threatening problem Serious problem

Cyber-terrorist attack hacker attack

Any relation between a set of documents and a

set of features naturally induces a network of

associations. Two features are associated if they

index a substantial set of common documents. The

association can therefore be weighted by a measure

on the set of shared documents. The network of

associations gives rise to a ' feature x feature'

symmetric matrix that can be analyzed using

standard data mining approaches like clustering,

factor analysis or latent semantic analysis. The

output of these methods heavily depends on the

choice of the association index. However, before

applying any data mining process, the structure of

the association network should be studied

independently from the measure of associations.

Table 2: Terminological variations identified between

terms in the terrorism corpus.

Operation type Term1 Variant Terms Links

Spelling trauma center trauma

centre

93 138

Lexical

inclusion

Modif food

contamina-

tion

pet food

contaminati

1799 2709

Insert severe OF-

poisoning

case

severe OF-

poisoning

medical

intervention

case

41 60

Head disaster

intervention

disaster

intervention

call

2884 4326

Lexical

substitu-

tion

Modif acute stress

disorder

posttraumat

ic stress

disorder

062

95 651

Head political

violence

threat

political

violence

campaign

810

125

385

WordNet

synonyms

Modif Trauma

severity

injury

severity

185 99

Head terrorist

financing

terrorist

funding

396 217

The study of this structure becomes

indispensable when features result from a complex

text analysis process like multi-word terms (MWTs)

extracted from abstracts in an automated procedure.

Since these terms result from an unsupervised

process, some amount of noise can be expected. The

idea is then to use standard association measures to

remove the most improbable associations. So,

instead of working on a numeric matrix, we consider

the binary matrix that indicates if an association

between two multi-word terms is possible or not,

without prejudice on its strength since it could result

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

530

from some bias in the term selection procedure.

Moreover, low frequency terms are essential when

seeking for rare information like emerging new

concepts and/or new relationships between concepts.

This symmetric binary matrix gives rise to a non

directed graph between multi-word terms. In the

case of a corpus of documents constituted randomly,

the structure of this graph corresponds to the usual

small world frequently observed on co-word graphs

(Ferrer and Solé, 2001). In some cases, the extracted

terminological network of possible associations

shows an unexpected structure. TermWatch aims to

extract terminological graphs and to reveal this

structure if it exists, based on advanced graph

algorithm theory.

3.3 Term Clustering

The linguistic significance of each relation can be

translated in terms of one of two possible roles:

COMP and CLAS. Ideally, COMP relations are

variations that induce near-semantic equivalence or

synonymy links such as spelling variants,

permutations, WordNet synonyms, one-word

modifier expansions and insertions. COMP relations

are used to form a prior category of tight semantic

clusters which serve as a first level of

agglomeration. There is an edge between two nodes

if one is a COMP variant of the other. By forming

connected components, we group terms for which

there is a sequence of variations in COMP. Since

variations in COMP link only close semantically

related terms, resulting connected components

portray terms from the same concept family.

Components are labeled by its most central term and

can be used as document descriptors. CLAS

relations are those that involve a topical shift

between two terms, i.e., where the head word is

different like head expansion and head substitution.

For instance, the shift of focus from “criminal

assault” to the victim in “criminal assault victim”.

This category of relations is used to aggregate the

components formed by COMP relations in an

agglomerative hierarchical process.

The strength of these links between components

can be measured by the number of variations across

them. In other to favor rare relations and eliminate

noise, each variation is weighted by the inverse of its

frequency in the corpus. Then the strength of the

link between two components is computed as

follows:

θ CLAS

(I,J)

d(I,J) =

where N(I,J) is the number of variations in a subset

of relations called CLAS that relate terms in I to

terms in J.

CLAS clusters can be then formed using any

graph clustering algorithm based on this valued

graph of components. TermWatch implements a

variant of Single Link Clustering called CPCL

(Classification by Preferential Clustered Link). The

principle is to select at each iteration edges that are

local maximums and merge iteratively together all

nodes related by such edges. The advantage of this

principle is that two nodes are merged not only

based on the strength of their relation but also by

considering all the relations in their neighborhood.

The system then merges the components with the

strongest relation at iteration t. We have shown in

(SanJuan and Ibekwe-SanJuan, 2006) that CPCL has

a unique possible output and avoids part of the chain

effect common to hierarchical clustering methods.

CPCL is also different from the variants of

hierarchical clustering (single, average, complete

link) because it considers the association between

components as an unordered set and at a given

iteration, more than one group of components can be

clustered at different similarity values. In the other

variants of hierarchical clustering, the similarity

values between pairs of items is an ordered set. We

refer the reader to this publication for a more formal

description as well as for a comparison with a larger

family of clustering algorithms (variants of single-

link, average link and variants of k-means).

3.4 Generating Association Graphs and

Formal Concepts

Clustering a large corpus of terms can lead to several

hundreds even if coherent clusters which are

difficult to visualize (cluttered image). We also need

to study the way in which these clusters are

associated to documents. Association mining task,

introduced by (Agrawal et al., 1993) will be used for

this purpose. In our context, it can be formulated

thus: each document is related to the clusters that

contain at least one term in the document. Clusters

are then considered as items and each document

defines an itemset. We shall call them document

itemsets. The set of items can be extended to other

fields (features) like authors. Given an integer

threshold S, a frequent itemset is a set of items that

are included in at least S document itemsets. There

is no fixed size for frequent itemsets. Frequent

itemset discovery in a data base allows us to reveal

hidden dependences in general. Frequent itemsets of

size one are just frequent terms or authors. Frequent

MAPPING KNOWLEDGE DOMAINS - Combining Symbolic Relations with Graph Theory

531

itemsets of size 2 induce an association graph where

nodes are items and there is a link between two

nodes i and j if the pair {i,j} is a frequent itemset.

The resulting association graph being generally

too dense to be visualized, it is usual to perform

feature selection based on some measures like

mutual information or log likelihood, to select most

relevant edges. This approach has two drawbacks.

First, the resulting graph structure depends on the

selected measure. Second, it is not adapted to

highlight larger itemsets (triplets or more). Indeed,

any frequent itemset defines a clique in the original

association graph. Clearly, if I={i1,...,in} is a

frequent itemset, then any pair ik, ip of elements in I

is a frequent itemset of size two and defines an edge

in the association graph but not necessarily on the

graph of selected edges using a relevance measure.

Thus all nodes i1,...,in are related in the original

association graph. It results that to visualize large

frequent itemsets on the association graph, we need

a decomposition graph approach that preserves

cliques induced by frequent itemsets.

The theoretical framework of association

discovery is Formal Concept Analysis (FCA) (Wille,

1982), (Priss, 2006) based on Galois lattice theory.

FCA offers a pragmatic way of formalizing the

notion of concepts. It posits that to every real

concept in a domain corresponds a formal concept in

some database of specialized documents. In the

present context, a formal concept consists of an

extension made of a set D of documents, and an

intension made of a set of items I such that a

document d is related to all items in I if and only if d

is in D. Thus a formal concept establishes an exact

correspondence between a set of documents and a

set of items. Frequent itemsets that are the intensions

of some formal concept are called closed itemsets.

We shall focus on graph decomposition methods that

preserve the cliques induced by closed frequent

itemsets.

3.5 Graph Decomposition

Not every clique in a graph induces a frequent

itemset, much less a closed frequent itemset.

Algorithms to enumerate all closed frequent itemsets

are exponential because the number of these

frequent itemsets can be exponential. Moreover they

are highly redundant. Thus, available packages to

mine them like state of the art arules from the R

project1 require the analyst to fix a maximal size for

mined itemsets. Interestingness measures are then

applied to rank them. However, the list of top ranked

frequent itemsets heavily depends on the choice of

this measure.

Our idea is to apply the results from recent

research on graph theory (Berry A. 2004) to extract

sub-graphs that preserve special cliques that have a

high probability to be closed frequent itemsets. We

focus on minimal clique separators, i.e. cliques

whose removal from the original graph will result in

several disjoint subgraphs. This leads to extracting

maximal sub-graphs without minimal clique

separators. These maximal sub-graphs are called

central atoms. By revealing the atomic structure of a

graph we also reveal: (i) special concepts that are

interfaces between sub-domains or between domain

kernels and external related objects; and (ii)

aggregates of intrinsically related concepts at the

heart of the domain. A key point of atom

decomposition is that it is unique. It is an intrinsic

graph property. It follows that the number of atoms

and their size distribution can be considered as good

indicators of their structure complexity. Moreover

the atomic structure can be computed in quadratic

time on the number of nodes: O(#vertex.#edges).

In the case of mapping the structure of a domain

based on a corpus of abstracts resulting from a

multi-word query, it can be expected to find the

concept corresponding to the query at the heart of

the association graph in a central atom. This central

atom should contain all concepts directly related to

the domain as sub-cliques. Some of them should

connect the domain with external concepts and thus

should be at the intersection of the central atom with

peripheral ones. The atom decomposition algorithm

is implemented in C++ program (Biha 2007). It

computes the atomic graph structure and generates

two images:

 the sub-graph that constitutes the central atom if

it exists.

 the network of atoms to visualize those at the

periphery and the way they are connected to the

central atom.

We have experimentally checked that atoms do not

break closed frequent itemsets at 98%. In the result

section, we shall focus on the central atom because

we found out that in the corpora analyzed here

(terrorism), they have a surprisingly clear structure.

Graph Visualization. The atom graphs are generated

in GDL format (Sander, 1995) for AiSee

(http://www.aisee.com). GDL allows to define sub-

graphs objects that can be displayed folded or

wrapped in a colored background. We use this

functionality to fold clique sub-graphs of nodes such

that the probabilities P(i/j) of finding one related to a

document knowing that the other is related are equal

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

532

for all pair of nodes in the clique. These cliques are

then represented by a generic node to simplify the

display of the graph without altering its structure.

We use AiSee because this software implements

optimized force direct graph display algorithms. To

analyze a complex graph structure. AiSee runs with

maximal non crossing heuristics and a great number

of iterations to approximate as far as possible a

planar graph without crossing edges and separating

non connected nodes clearly. The resulting images

allow experts to quickly identify the main structural

properties of the graph: maximal cycle length,

connectivity, sub-cliques etc. Moreover, since nodes

are labeled, domain specialists can also easily read

these graphs using the browsing function of AiSee.

4 A CASE STUDY

We present in this appendix results on mapping the

dynamics of research in terrorism research between

1990-2006. Table 4 gives the parameters set for

clustering terms and some general statistics.

Table 3: Clustering parameters set for the two corpora:

Terrorism and SDSS.

Nb of input records 3 366

Similarity threshold 0

Nb of iterations 4

Nb of clusters 1 676

Nb of components 2 547

Nb of terms in clusters 4 816

Size biggest component 35

Size biggest cluster 79

Our earlier experimentations on different corpora

have shown that variations in the two clustering

parameters, threshold and iterations do not alter

much the clustering results. In the current

experiment, we tried several similarity thresholds (0,

0.01, 0.001) for both corpora and found no

significant variation. Most graphs converged at the

4th iteration. This tended to show that the method is

stable vis-à-vis corpora from different domains.

Indeed, the linguistic variations used as clustering

relations are generic and tend to be present in similar

proportions across different scientific domains. We

are currently working on setting default parameters

in TermWatch so as to enable the user to concentrate

more on results exploration.

4.1 Structure of the Central Atom

Colours are used to code the clusters according to a

time-slicing of the corpus. The colour of a node

indicates two types of temporal information. The

center of a cluster (depicted by a circle) or a

component (box) shows the start peak period in

which most of the constituent terms appeared. The

colour of the ring around a cluster depicts the end of

the peak period. For instance, a cluster with a pink

center and a bright green ring indicates that most of

its terms occurred in the period 1997-1999 (pink

center) until 2002 (light green ring). The ring shows

the last peak period before decline.

The use of colour codes gives a temporal

dimension for tracking research topics evolution.

Clusters are automatically labeled by the system as

the term with the highest number of semantic

variants.

Figure 2: Time slice and colour code of clusters for

terrorism corpus.

Figure 3: Internal structure of the central atom on

“biological terrorism”.

TermWatch identified a central atom labelled

biological terrorism. This graph can be unfolded to

show its internal structure (figure 3). We can clearly

perceive three sub-graphs of clusters with some

connections between them.

The topmost sub-graph reflects research on the

psychological aftermath of september 11, 2001

attacks, namely posttraumatic stress disorders

(PTSD). The lower part of the graph reflects

research on potential terrorists attacks using

biological and nuclear weapons. The structure of

MAPPING KNOWLEDGE DOMAINS - Combining Symbolic Relations with Graph Theory

533

these three sub-graphs echoes the network found in

Chen (2006) for the period 1990-2003.

Figure 4 displays top-most subgraph. The first

noticeable thing in this sub-group is the domination

of red colour, indicating that the majority of terms in

these clusters appeared in the last period (2006).

This sub-graph (see figure 4) corresponds roughly to

the most prominent thread found in Chen (2006) on

“September 11” and “posttraumatic stress-disorder”

(PTSD). This last term is still very much present

three years later years as shown by terminological

variations found around this term, both in its

developed form (posttraumatic stress disorder

symptom) and in abbreviated forms (probable PTSD

frequency, PTSD symptom severity, SCW-PTSD

prevalence (SCW = symptoms consistent with).

Figure 4: Upper subgraph from Figure 3.

At the center of this sub-graph is the author node

“Boscarino_JA” (arrow origin in Figure 4). To

understand the central position of the author

“Boscarino_JA”, we queried the MySQL database to

access the bibliographic records of publications of

this author. Dr Joseph A. Boscarino co-authored 22

papers in the period covered by our corpus, all

published between 2004-2006, the last period of the

corpus, hence the red colour of the cluster. His

papers focused on psychological effects and PTSD

caused by the 9/11, 2001 event. Among the pre-

occupying health issues brought to light by this

research thread is the increased use of drugs, alcohol

and the increase in mental disorder among the

population in the area surrounding the World Trade

Center. This is evident in the surrounding cluster

labels: physical health, psychological health (double

arrow edge in Figure 4), binge drinking, alcohol use,

increased substance use, african-american,

posttraumatic stress disorder symptom, psychotropic

medication (simple arrow edge in Figure 4).

The system also computes statistical indicators

from the Social Network Analysis (Freeman, 1977)

in order to characterize the relative position of nodes

and their importance in the network. We show below

the first 20 nodes ranked by betweenness centrality.

Table 4: First 20 clusters ranked by betweenness

centrality. Terrorism corpus.

centrl. dens. betw. degree freq. mean node

0.0 0.0 214336 162.0 3.2 4.2 posttraumatic stress disorder

0.1 0.0 91637 81.0 1.8 4.2 same traumatic event

0.1 0.0 76126 68.0 1.7 4.1 world health

0.1 0.0 67951 54.0 1.8 4.2 suicidal terrorist bombing

0.0 0.0 65879 53.0 0.9 4.6 world trade center

0.3 0.1 62483 83.0 4.1 4.1 biological terrorism

0.1 0.1 62296 43.0 1.5 3.7 mass destruction

0.2 0.1 60768 48.0 3.1 4.3 specific injury type

0.1 0.0 59095 70.0 1.6 4.5 new york city

0.3 0.2 51682 38.0 1.5 4.6 domestic law enforcement

0.2 0.1 50271 49.0 1.5 4.2 potential biological weapon

0.1 0.0 48571 42.0 1.0 4.2 unmet mental health

0.5 0.4 44095 30.0 1.0 5.5 national security

0.2 0.1 41590 34.0 1.1 4.3 recent natural disaster

0.6 0.5 41019 25.0 3.5 5.7 domestic air travel

0.1 0.1 39136 42.0 1.6 4.1 mass destruction weapon

0.1 0.0 37480 31.0 0.7 4.0 biological agent

0.1 0.0 37184 38.0 1.9 4.7 primary blast injury

0.4 0.2 36744 61.0 5.4 4.1 premeditated biologic attack

0.4 0.2 36167 48.0 2.1 4.0 recent bioterrorist attack

Nodes with high betweenness centrality values

are possible transitions points from one research

thread to another. 1st column, 'centrality' is

calculated as a normalized number of edges in the

neighbourhood. 2nd column, 'density' is computed as

a valued version of centrality. The 3rd column is the

betweenness centrality which is the number of

geodesics crossing the node. 4th column, 'degree' is

the number of adjacent edges. The 5th column

'frequency' is a valued version of degree. 6th column

'mean' is the average of the distance between the

node and the others.

We observe that some of the prominent themes

present in the central atom, in the three sub-graphs

are ranked in the topmost positions: posttraumatic

stress disorder (PTSD) is also the first node by

betweenness centrality. The other topmost nodes all

recall major terrorist threats (same traumatic event,

world health, suicidal terrorist bombing, biological

terrorism, mass destruction). The three research

threads portrayed by the three sub-graphs in the

central atom are present in the first 20 nodes by

betweenness centrality: posttraumatic stress

disorder (1st), specific injury type (8th), primary

injury blast (18th), biological terrorism (6th).

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

534

4.2 Mining Closed Frequent Itemsets

on Terrorism Research

For complexity reasons, it is not possible to extract

frequent itemsets whose extension has fewer than

three documents, meanwhile we shall see that the

atom graph allows us to identify interesting closed

itemsets whose extension has only two documents.

Using the apriori algorithm in R package, we found

1926 closed itemsets with a support of at least three

documents of which 285 have more than three

elements (three items). The largest closed frequent

itemset without author names is: {new york city,

posttraumatic stress disorder, potential terrorist

attack, same traumatic event, world trade center}.

The largest overall has 12 items: {Parker_G,

Perl_TM, Russell_PK}, biological terrorism,

biological warfare, consensus-based

recommendation, emergency management

institution, MEDLINE database, nation civilian

population, potential biological weapon, working

group, world health}. Despite differences in length,

these two itemsets both have the same support: their

extension has three documents.

5 CONCLUSIONS

We have presented a platform for mapping the

dynamics of research in specialty fields. The

distinctive features of this methodology resides in its

clustering algorithm which is based primarily on

linguistic (symbolic) relations and on its graph

decomposition algorithm which renders complex

terminological graph for comprehensible for domain

analysts. The method has been able to identify the

most salient topics in two different research domains

and uncover the sub-structures formed by persistent

and evolving research threads. More importantly, we

have shown that it is possible, with limited linguistic

resources, to perform a surface analysis of texts and

use linguistic relation for clustering. To the best of

our knowledge, this represents a unique and

innovative approach to text clustering.

The graph decomposition algorithm offers a way

of visualizing complex terminological graphs and

revealing particular sub-structures contained therein.

Mining frequent itemsets, in combination with

evaluation by human experts, offer a joint and strong

evidence of the significance of the maps produced

for the domain.

ACKNOWLEDGEMENTS

This work was supported in part by the the French

National Research Agency CAAS project (ANR

2010 CORD 001 02).

REFERENCES

Agrawal R., Imielinski T., Swami A., Mining association

rules between sets of items in large databases. In ACM

SIGMOD Conf. Management of Data, May 1993.

Bar-Ilan J., Informetrics at the beginning of the 21

century

– A review, Journal of Informetrics, 2008, 2, 1-52

Berry A., Krueger R., Simonet G., Ultimate Generaliza-

tions of LexBFS and LEX M. WG 2005: 199-213.

Berry, M. W. (eds)., Survey of Text Mining, Clustering,

Classification and Retrieval, Springer, 2004, 244p.

Callon M., Courtial J-P., Turner W., Bauin S. , From

translation to network: The co-word analysis.

Scientometrics, 1983, 5(1).

Castellanos M., HotMiner: Discovering hot topics from

dirty texts, in Berry M. W. (dir.), Survey of Text

Mining Systems, Springer Verlag, NY, 2004, 123-157.

Chalmers M., Using a landscape metaphor to represent a

corpus of documents. In Spatial Information theory,

Frank A., Caspari I. (eds.), Springer Verlag LNCS

716, 1993, 377-390.

Chen C., CiteSpace II: Detecting and visualizing emerging

trends and transient patterns in scientific literature.

Journal of the American society for Information

Science, 2006, 57(3), 359-377.

Chen C., Ibekwe-SanJuan F., SanJuan E., Weaver C.,

Visual Analysis of Conflicting Opinions, 1st

International IEEE Symposium on Visual Analytics

Science and Technology (VAST 2006), Baltimore -

Maryland, USA, 31 Oct.-2 Nov. 2006, 59-66.

Chen H., Wingyan C., Qin J., Reid E., Sageman M.,

Uncovering the dark web: A case study of jihad on the

web. Journal of the American society for Information

Science, 2008, 59(8), 1347-1359.

Church K. W., Hanks P., Word association norms, mutual

information and lexicography, Computational

Linguistics, 16, n° 1, 1990, 22-29.

Cutting D., Pedersen J. O., Karger D., Tukey J. W.,

Scatter/Gather: A cluster based approach to browsing

large document collections. In Proceedings of the 15

Anuual ACM/SIGIR Conference, Copenhagen,

Danemark, 1992, 318-329.

Freeman L. C., A set of measures of centrality based on

betweenness, Sociometry, 1977, 40(1), 35–41.

Mane K. K, Borner K., Mapping topics and topic bursts,

Proceedings of the National Academy of Sciences,

USA (PNAS), 2004, 101 (suppl. 1), 5287-5290

Morris S. A., Martens B., Modeling and Mapping of

Research Specialties, Annual Review of Information

Science and Technology, 42, 2008, 52p.

MAPPING KNOWLEDGE DOMAINS - Combining Symbolic Relations with Graph Theory

535

Morris S. A., Yen G. G., Crossmaps: Visualization of

overlapping relationships in collections of journal

papers, PNAS, 2004, 101 (suppl. 1) 5291-5296.

Priss U., Formal Concept Analysis in Information Science.

Cronin, Blaise (ed.), Annual Review of Information

Science and Technology, 2006, 40, 521-543.

Prize L., Thelwall M., The clustering power of low

frequency words in academic webs. Journal of the

American Society for Information Science and

Technology, 2005, 56 (8), 883–888.

Sander G., Graph Layout through the VCG Tool, in

Tamassia, Roberto; Tollis, Ioannis G., Editors: Graph

Drawing, DIMACS International Workshop GD'94,

Lecture Notes in Computer Science 894, 1995, 194 -

205.

SanJuan E., Ibekwe-SanJuan F. Textmining without

document context. Information Processing &

Management, Special issue on Informetrics II,

Elsevier, 2006, 42(6), 1532-1552.

SanJuan E., Dowdall J., Ibekwe-SanJuan F., Rinaldi F. A

symbolic approach to automatic multiword term

structuring. Computer Speech and Language (CSL),

Special issue on Multiword Expressions, Elsevier,

2005, 19 (4), 524-542.

Wille R., Restructuring lattice theory: an approach based

on hierarchies of concepts. Ordered Sets (I. Rival, ed.),

Reidel, Dordrecht-boston, 1982, 445–470.

KDIR 2011 - International Conference on Knowledge Discovery and Information Retrieval

536