APPLICATION OF MULTIVARIATE EMPIRICAL MODE

DECOMPOSITION FOR CLEANING EYE BLINKS ARTIFACTS

FROM EEG SIGNALS

Esteve Gallego-Jutglà

, Jordi Solé-Casals

, Tomasz M. Rutkowski

2,3

and Andrzej Cichocki

Digital Technologies Group, University of Vic, Sagrada Família 7, 08500 Vic, Spain

LABSP, RIKEN Brain Science Institute, 2-1 Hirosawa, Saitama, 351-0106 Wako-Shi, Japan

Multimedia Lab, Computer Science Department & Tara Life Science Center, University of Tsukuba, Tsukuba, Japan

Keywords: EEG, mEMD, EMD, Artifacts, Eye blinks.

Abstract: Eye movements and eye blinks are present in most of the electroencephalography (EEG) recordings, making

it difficult to interpret or analyze the data. In this paper an extension of empirical mode decomposition

(EMD) is proposed in order to clean EEG data of eye blinks artifacts. This is achieved by applying two

cleaning methods to EEG simulated data. One of these methods is presented only for illustrative purposes,

whereas the second one can be applied to real EEG data. The results show that the cleaned data with both

these methods presents high correlation (

>0.8) with the simulated EEG clean data.

1 INTRODUCTION

Eye movements and eye blinks are undesired signals

that can introduce significant changes in the

recording of brain signals. Electric potentials due to

these artifacts can be orders of magnitude larger than

the electroencephalogram (EEG) and can propagate

across the scalp, masking and distorting brain

signals (Croft and Barry, 2000).

This paper focuses on removal of eye blinks

artifacts from EEG data using a new signal

processing technique, Multivariate Empirical Mode

Decomposition (mEMD). This technique is an

extension of the Empirical Mode Decomposition

(EMD), and provides a decomposition of the

original EEG data into several oscillatory modes

computed along multichannel data (Rehman and

Mandic, 2010). Recently it was shown that EMD is a

good method to separate eye movements from

neurophysiological signals as pointed out in

(Rutkowski et al., 2009a, Rutkowski et al., 2009b),

where results were obtained comparing the extracted

modes with the modes of the EOG.

This paper presents a new strategy for removing

eye blinks artifacts in EEG data using the mEMD

technique. In this strategy only the EEG electrodes

information is used. Two cleaning methods are

presented, and compared. The first one of these

methods is a non-realistic one, based on the use of

clean and raw EEG data, while the second one uses

only raw EEG data. These two methods are

presented in order to show that they are (almost)

equivalent and, therefore, the second method can be

used in real applications.

This paper is organized as follows. First,

methods used, including simulated data generation,

EMD and mEMD description and both cleaning

methods, are presented in Section 2. Section 3

describes the experimental results obtained with

these cleaning methods. Finally, discussion and

conclusions are presented in Section 4.

2 METHODS

EEG signals recorded on the scalp are usually highly

contaminated by various artifacts. Eye blinks are

quite often the largest ones. Typical duration of an

eye blink is 200–400 ms, and its spectral signature

spans the δ and θ range (Croft and Barry, 2000),

with most of the energy located below 5 Hz.

To eliminate eye blink artifacts, the use of

multivariate EMD (mEMD) is proposed. mEMD is

a new technique to decompose EEG data based on

EMD. mEMD decomposition is applied to simulated

EEG data and then data is cleaned using two

455

Gallego-Jutglà E., Solé-Casals J., M. Rutkowski T. and Cichocki A..

APPLICATION OF MULTIVARIATE EMPIRICAL MODE DECOMPOSITION FOR CLEANING EYE BLINKS ARTIFACTS FROM EEG SIGNALS.

DOI: 10.5220/0003722004550460

In Proceedings of the International Conference on Neural Computation Theory and Applications (Special Session on Challenges in Neuroengineering-

2011), pages 455-460

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

different methods. In the first method the

decompositions obtained for clean and raw EEG

data are compared in order to investigate how

artifacts affect those modes. This is not applicable in

real cases as we do not have access to clean EEG (in

fact that is what we are looking for, using cleaning

procedures). The second method is based on mEMD

of only raw EEG data, the truly accessible signals in

real applications, and is shown to be equivalent to

the first one.

2.1 Simulated Data

In order to compare these two methods, detailed in

section 2.4, the EEG activity of 15 scalp electrodes

were simulated, 10-s of data with eye blinks (raw

EEG data) and 10-s of data without eye blinks (clean

EEG data), as shown in Figure 1. It is important to

have this raw and clean EEG data in order to

compare the results of the cleaning procedure.

Figure 1: A 5-sec portion of the simulated raw EEG time

series, with eye blinks (top image). A 5-sec portion of the

simulated clean EEG time series, without eye blinks

(bottom image).

For each realization, 4 independent cerebral

sources were simulated using the following

equation:

SourceActivit

=sin



2







(1)

Cerebral sources were simulated in different

frequency range (α, β, γ and μ), with consistent

location in the cortex (Kropotov, 2009) and a

sampling rate of 128 Hz. Eye blinks time series were

manually extracted using ICA decomposition on real

data. The real data was initially sampled at 1 kHz,

and before the application of ICA decomposition,

data was filtered with a band-pas filter (1 Hz- 50 Hz)

and resampled to 128 Hz with the Natural Cubic

Spline Interpolation (Congedo et al., 2002). Then,

eye blinks components of the ICA decomposition

were visually identified and extracted by its time

course and scalp topography (high gains on frontal

electrodes, small gains elsewhere) (Jung et al.,

2000).

Simulated EEG signals were derived from the

simulated cerebral sources and the extracted eye

blinks components, by multiplying by a mixing

matrix specifying the projection of each model

dipole to each sensor as sown here:

Φ=KJ+n (2)

Where vector Φ contains instantaneous scalp

electric potential differences measured at the

electrodes,J is the vector representing the impressed

current densities on the cortex (the simulated

sources), n is additive white noise, uncorrelated

withΦ, and K is the lead field matrix, which holds

the relationship between sources position and

electrodes position (Pascual-Marqui, 2002). Matrix

K was created using the low resolution brain

electromagnetic tomography software LORETA

(free publicly available academic software at http://

www.uzh.ch/keyinst/loreta.htm).

2.2 Empirical Mode Decomposition

(EMD) Applied to EEG Signals

EMD algorithm is a method designed for multiscale

decomposition and time –frequency analysis, which

can analyze nonlinear and non-stationary data

(Huang et al., 1998).

The key part of the method is the decomposition

part in which any time-series data set can be

decomposed into a finite and often small number of

Intrinsic Mode Functions (IMFs). These IMFs are

defined so as to exhibit locality in time and to

represent a single oscillatory mode. Each IMF

satisfies two basic conditions: (i) the number of

zero-crossings and the number of extrema must be

the same or differ at most by one in the whole

dataset, and (ii) at any point, the mean value of the

envelope defined by the local maxima and the

envelope defined by the local minima is zero (Huang

et al., 1998).

The EMD algorithm (Huang et al., 1998) for the

signal 







can be summarized as follows.

(i) Determine the local maxima and minima of









;

NCTA 2011 - International Conference on Neural Computation Theory and Applications

456

(ii) Generate the upper and lower signal

envelope by connecting those local maxima and

minima respectively by an interpolation method;

(iii) Determine the local mean









, by

averaging the upper and lower signal envelope;

(iv) Subtract the local mean from the data:

ℎ









=







−









(v) If ℎ









 obeys the stopping criteria, then we

define







=ℎ









as an IMF, otherwise set









=ℎ









and repeat the process from step i.

Then, the empirical mode decomposition of a

signal







can be written as:





=IMF







+ε











(3)

Where n is the number of extracted IMFs, and

the final residue ε







is the mean trend or a

constant.

2.3 Multivariate Empirical Mode

Decomposition (mEMD) Applied to

EEG Signals

EMD has achieved optimal results in data processing

(Diez et al. 2009, Molla et al., 2010). However, this

method presents several shortcomings in

multichannel datasets. The IMFs from different time

series do not necessarily correspond to the same

frequency, and different time series may end up

having a different number of IMFs. For

computational purpose, it is difficult to match the

different obtained IMFs from different channels

(Mutlu and Aviyente, 2011).

To solve these shortcomings, an extension of

EMD to mEMD is required. In this approach the

local mean is computed by tanking an average of

upper and lower envelopes, which in turn are

obtained by interpolating between the local maxima

and minima. However, in general, for multivariate

signals, the local maxima and minima may not be

defined directly. To deal with these problems

multiple n-dimensional envelopes are generated by

taking signal projections along different direction in

n-dimensional spaces (Rehman and Mandic, 2010).

mEMD is the technique used in this paper to

compute all the decompositions.

The algorithm (Rehman and Mandic, 2010) can

be summarized as follows.

(i) Choose a suitable pointset for sampling on an



−1



sphere (this



−1



 sphere resides in an 

dimensional Euclidean coordinate system).

(ii) Calculate the projection, p















, of the

input signal v









along the direction vector, x





for all k giving p















(iii) Find the time instants t







corresponding to

the maxima of the set of projected

signalsp















(iv) Interpolate t







,vt







 to obtain

multivariate envelope curvese















(v) For a set of K direction vectors, the mean of

the envelope curves is calculated as 







⁄∑













(vi) Extract the detail 







using 







=







−









. If the detail 







fulfills the stopping criteria

for a multivariate IMF, apply the above procedure

to







−







, otherwise apply it to 







Then, the mEMD of a signal x







can be written

as detailed in equation 3. An example of the

application of mEMD to 5 seconds of EEG time

series with eye blinks is shown in Figure 2.

Figure 2: mEMD of 5-sec portion of the simulated raw

EEG time series (i.e. with eye blinks) at sensor FP1. The

original time series is presented in the first line (Sen). A

total of 10 IMFs are obtained for this signal.

2.4 mEMD Cleaning Procedure

2.4.1 Cleaning Method 1

The first method is based on the comparison of IMFs

obtained from the multivariate empirical mode

decomposition in the two data sets (raw data and

clean data). The key idea is to decompose each data

set and determine the similarity between modes by

means of correlation coefficients. As the only

difference between these two data sets is the

presence/absence of eye blinks, the cleaning

procedure will be focused on eliminating the modes

that are not similar in both cases, meaning that these

modes are those that appear due to eye blinks.

Therefore, the correlation between IMF of the

EEG data with eye blinks was computed with the

corresponding IMF pair of EEG data without eye

APPLICATION OF MULTIVARIATE EMPIRICAL MODE DECOMPOSITION FOR CLEANING EYE BLINKS

ARTIFACTS FROM EEG SIGNALS

457

blinks. IMFs that presented a low correlation

(

<0.8) were eliminated from the data before

reconstruction. This analysis was performed for each

one of the 15 electrodes existing in the dataset.

2.4.2 Cleaning Method 2

In real world applications raw data will be the only

available data. Therefore, no comparison can be

made between the mEMD decomposition and any

reference (for example, the one obtained applying

mEMD to the same cleaned data, as in the previous

case). This is why a second procedure is proposed in

order to remove eye blinks from the data.

Here the key idea is to consider that if a mode

appears in (most of) all the electrodes, this mode

cannot be due to neurological activity and therefore

it’s considered as an artifact. Note that now the only

data used is the raw EEG data (the only available

data in real applications), and common modes are

sought in the mEMD decomposition of this data.

mEMD cleaning method 2 can be summarized as

it follows:

(i) Apply mEMD to raw EEG data (EEG with

eye blinks), in order to obtain oscillatory modes of

the multivariate data.

(ii) Construct a matrix containing the same mode

of all the channels. Therefore the total number of

matrices will be equal to the number of modes we

obtained.

(iii) Calculate the correlation matrix of each one

of these previous matrices.

(iv) Calculate the mean correlation of each

channel for each mode, obtaining a vector that

contains the degree of communality of each mode

(i.e. a measure of how this mode is present in all the

electrodes). Normalize this vector in order to have

values between 0 and 1.

(v) Threshold the previous vector in order to find

which of these modes is common within all the

channels. Modes with high correlation (

>0.8)

are eliminated

(vi) Reconstruct clean signals without taking into

account the eliminated modes

3 RESULTS

In order to compare the performance of each

cleaning procedure, we compute the correlation

between signals at each electrode of the cleaned data

(using cleaning method 1 or cleaning method 2) and

simulated clean EEG data (EEG data without eye

blinks). The power spectra were also computed in

order to compare the differences in the frequency

domain.

Table 1 shows the eliminated modes with each

cleaning method. Reconstructed signals were

computed without those IMFs.

Table 1: Eliminated IMFs for each cleaning method.

Sensors Eliminated IMFs

Method 1

Fz and O1 4, 5, 6, 7, 8 and 9

F4, C3, P4, P3,

T5, T6 and O2

4, 5, 6, 7, 8, 9 and 10

F3 and C4

4, 5, 6, 7, 8, 9 and ε







FP1, FP2, Cz

and Pz

4, 5, 6, 7, 8, 9, 10 and ε







Method 2

All sensors

4,5,6,7,8,9, 10 and ε







As can be seen in Table 1, results are very

similar, differing only on the final IMF 10 and the

residue

ε







. For the cleaning method 1 some

sensors kept those modes and some sensors

eliminate them, whereas cleaning method 2

eliminated all IMF form IMF 4 to IMF 10 and the

residue

ε







The correlation between reconstructed data with

method 1 and method 2 and the simulated clean

EEG signal (without eye blinks) is presented in

Figure 3. This figure also shows (blue bars) the

correlation between the original raw EEG data (with

eye blinks) and the clean EEG data (without eye

blinks)

Clearly it can be seen that eye blinks disturb

EEG data in such a way that correlation between raw

EEG and clean EEG is very low in all the electrodes

(blue bars in Figure 3), and especially in frontal

electrodes FP1 and FP2, as they are close to eyes.

Using cleaning procedures to eliminate eye blinks

allows us to recover an approximation of clean EEG

data, and this can be observed in the correlation of

data between clean EEG and cleaned EEG data at

each electrode, whatever method is used (green and

brown bars in Figure 3).

Initial correlation of data with eye blinks is

highly improved with both two cleaning procedures,

with correlation values

>0.8. Despite no

significant differences between the two cleaning

methods, cleaning method 2 always presents higher

correlation than cleaning method 1.

The power spectra of the frontal electrodes (FP1 and

FP2) are presented in Figure 4. Results show that the

simulated EEG data with eye blinks (blue line)

presents more power in the low frequencies, whereas

no such power appears in the power spectra of the

EEG data without eye blinks (black line). Even if the

reconstructed

signal with method 2 (red line)

NCTA 2011 - International Conference on Neural Computation Theory and Applications

458

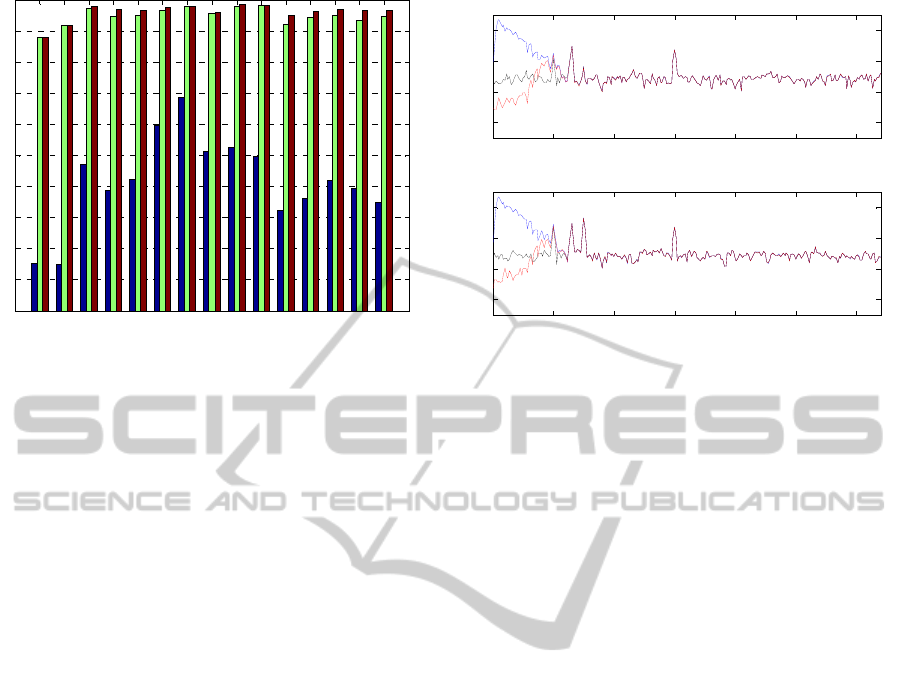
Figure 3: Correlations, at each sensor, of the simulated

clean EEG with raw EEG data (blue), cleaned EEG data

with cleaning method 1 (green) and cleaned EEG data

with cleaning method 2 (red).

presents less power spectra in the low frequencies

than the clean EEG data, its shape is more similar to

the (original) clean EEG data than the raw data, and

no differences can be observed in the higher

frequencies (α, β and γ range) between them.

4 DISCUSSION AND

CONCLUSIONS

In this paper a new procedure for cleaning eye blink

artifacts in EEG data is presented. This new method

is based on a novel EEG decomposing technique,

which allows flexible signal decomposition of the

original time series in different oscillatory modes.

The so-obtained components from each EEG

channel have been analyzed using two different

strategies. In method 1, the obtained IMFs have been

compared with the IMFs from artifacts-clean EEG

data and those that presented low correlation

havebeen eliminated in the reconstruction process.

On the other hand, in method 2 the obtained IMFs of

the raw EEG data of all electrodes have been

compared among themselves, and those that are

present in all the electrodes have been eliminated in

the reconstruction process. Resulting reconstruction

in both methods allowed us to separate eye blinks

artifacts from brain activity.

The two methods presented in this article

achieved a suppression of the eye blinks artifacts.

However, method 1 is based on the comparison of

raw EEG data with clean EEG data (that is not

available in real scenarios), therefore is not a useful

method

and was presented here for illustrative

Figure 4: Power spectra of the frontal electrodes FP1

(upper image) and FP2 (bottom image). In blue, the power

spectra of the simulated raw EEG data (with eye blinks);

in black, the power spectra of the simulated clean EEG

data (without eye blinks); and in red, the power spectra of

the reconstructed data with cleaning method 2.

purposes. On the other hand, method 2 uses only raw

EEG data and in our experiments has been shown to

be (almost) equivalent to method 1, giving the same

or better results in cleaning eye blinks artifacts.

The eliminated modes presented in Table 1

correspond to low frequency oscillation. These

results are consistent with previous knowledge of

eye blinks artifacts, in which the artifact interference

is found in the low frequencies.

Finally, results in Figure 4 show that power

spectra due to the eye blinks artifacts in δ and θ

bands are clearly suppressed, whereas the power in

the higher frequency range (α, β and γ bands) do not

present significant differences.

These results point out that the use of mEMD to

correct eye blinks may be a good procedure for EEG

signal preprocessing, a necessary step to be taken

before any kind of EEG signal analysis.

Future work will include the comparison of this

method with ICA-based cleaning procedures (Solé-

Casals et al., 2010), or Wavelet-based cleaning

procedures (Krishnaveni et al., 2006, Vialatte et al.,

2008), and optimization of the computational load in

order to obtain a real-time system.

ACKNOWLEDGEMENTS

The authors would like to express their gratitude to

the reviewers for their valuable suggestions. This

work has been partially supported by the Fundación

Alicia Koplowitz to Dr. Jordi Solé-Casals, and by the

FP1 FP2 F3 FZ F4 C3 CZ C4 P3 PZ P4 T5 T6 O1 O2

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 10 20 30 40 50 60

-6

-4

-2

Sensor FP1

log(magnitude)

[Frequency]

0 10 20 30 40 50 60

-6

-4

-2

Sensor FP2

log(magnitude)

[Frequency]

APPLICATION OF MULTIVARIATE EMPIRICAL MODE DECOMPOSITION FOR CLEANING EYE BLINKS

ARTIFACTS FROM EEG SIGNALS

459

University of Vic under de grant R0904.

REFERENCES

Congedo, M., Ozen, C., Sherlin, L. (2002). Notes on EEG

resampling by natural cubic spline interpolation.

Journal of Neurotherapy, 6(4).

Croft, R. J., Barry, R. J., (2000). Removal of ocular

artefact form the EEG: a review. Neurophysiol

Clin,30, 5-19.

Diez, P. F., Mut, V., Laciar, E., Torres, A., Avilla, E.

(2009). Application of the Empirical Mode

Decomposition to the Extraction of Features form

EEG signals for Mental Task Classification. 31

Annual International Conference of the IEEE EMBS.

2579-2582.

Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H.

H., Zheng, Q., Yen, N. C., Tung, C. C., Liu, H. H.

(1998). The empirical mode decomposition and the

Hilbert spectrum for nonlinear and non-stationary time

series analysis. Proc. R. Soc. Lond., 495, 2317-2345.

Jung, T. P., Makeig, S., Westerfield, M., Townsend, J.,

Courchesne, E., Sejnowski, T. J. (2000). Removal of

eye artifacts from visual event-related potentials in

normal and clinical subjects. Clinical

Neurophysiology, 111, 1745-1758.

Kropotov, J. D., (2009). Quantitative EEG Event-Related

Potentials and Neurotherapy. (1st ed.). San Diego:

Academic Press.

Krishnaveni, V., Jayaraman, S., Aravind, S.,

Hariharasudhan, V., Ramadoss, K. (2006). Automatic

Identification and Removal of Ocular Artifacts from

EEG using Wavelet Transform. Measurement Science

Review, Vol. 6, Sec. 2, No. 4.

Molla, K. I., Tanaka, T., Rutkowski, T. M., Cichocki, A.,

(2010). Separation of EOG artifacts from EEG singals

using bivariate EMD. Acoustics Speech and Signal

Processing (ICASSP), 2010 IEEE Interational

Conference On. 562-565.

Mutlu, A. Y., Aviyente, S. (2011). Mutivariate Empirical

Mode Decomposition for Quantifying Multivariate

Phase Synchronization. EURASIP Jounal on Advances

in Signal Processing. Article ID 615717.

Pascual-Marqui, R. D. (2002). Standardized low resolution

brain electromagnetic tomography (sLORETA):

technical details. Methods Find. Exp. Clin.

Pharmacol.,24D, 5-12.

Rehman, N., Mandic, D. P., (2010). Multivariate empirical

mode decomposition. Proc. R. Soc. A. 466, 1291-

1302.

Rutkowski, T. M., Cichocki, A., Tanaka, T., Mandic, D.

P., Cao, J., Ralescu, A. L., (2009a). Multichannel

spectral pattern separation – An EEG processing

application. 2009 IEEE International Conference on

Acoustics, Speech and Signal Processing.

Rutkowski, T. M., Cichocki, A., Tanaka, T., Ralescu, A.

L., Mandic, D. P., (2009b). ICONIP’08 Proceedings

of the 15

international conference of Advances in

neuro-information processing. Vol Part I.

Solé-Casals, J., Vialatte, F. B., Pantel, J., Prvulovic, D.,

Haenschel, C., Cichocki, A.: ICA Cleaning Procedure

for EEG Signals Analysis - Application to Alzheimer's

Disease Detection. BIOSIGNALS 2010: 484-489

Vialatte, F. B., Solé-Casals, J., Cichocki, A. (2008). EEG

windowed statistical wavelet scoring for evaluation

and discrimination of muscular artifacts. Physiol.

Meas. 29 1435–1452.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

460