STATISTICAL ANALYSIS OF FUNCTIONAL MRI DATA USING

INDEPENDENT COMPONENT ANALYSIS

M. Bartés-Serrallonga

, J. Sole´-Casals

, A. Adan

2,3

, C. Falcón

4,5

, N. Bargalló

and J. M. Serra-Grabulosa

2,4

Digital Technologies Group, University of Vic, Vic, Spain

Departament de Psiquiatria i Psicobiologia Clínica, Universitat de Barcelona, Barcelona, Spain

Institute for Brain, Cognition and Behaviour (IR3C), Barcelona, Spain

Institut d’Investigacions Biomèdiques August Pi i Sunyer (IDIBAPS), Barcelona, Spain

CIBER-BBN, Barcelona, Spain

Secció de Neuroradiologia, Servei de Radiologia, Centre de Diagnòstic per la Imatge (CDI)

Hospital Clínic de Barcelona, Barcelona, Spain

Keywords: Functional magnetic resonance imaging, Independent component analysis, BOLD.

Abstract: Functional magnetic resonance imaging (fMRI) is a technique to map the brain, anatomically as well as

physiologically, which does not require any invasive analysis. In order to obtain brain activation maps, the

subject under study must perform a task or be exposed to an external stimulus. At the same time a large

amount of images are acquired using ultra-fast sequences through magnetic resonance. Afterwards, these

images are processed and analyzed with statistical algorithms. This study was made in collaboration with

the consolidated Neuropsychology Research Group of the University of Barcelona, focusing on applications

of fMRI for the study of brain function in images obtained with various subjects. This group performed a

study which analyzed fMRI data, acquired with various subjects, using the General Linear Model (GLM).

The aim of our work was to analyze the same fMRI data using Independent Component Analysis (ICA) and

compare the results with those obtained through GLM. Results showed that ICA was able to find more

active networks than GLM. The activations were found in frontal, parietal, occipital and temporal areas.

1 INTRODUCTION

Functional Magnetic Resonance Imaging (fMRI) is a

technique that provides the opportunity to study

noninvasively which parts of the brain are activated

by different types of stimulation or activity, such as

sight, sound or movement. This technique measures

the Blood Oxygenation Level Dependent (BOLD)

contrast, which is based on the differing magnetic

properties of oxygenated (diamagnetic) and

deoxygenated (paramagnetic) blood. When brain

neurons are activated, there is a change in blood

flow and oxygenation that causes a change in the

Magnetic Resonance (MR) signal which is received

by the receiver coils. A higher level of oxygenated

blood in a located area means that there is an

increase in neural activity in this area. On the other

hand, a lower level means the opposite (D’Esposito

et al., 1999).

In order to capture the effect of BOLD contrast,

the subject lies in the magnet under the influence of

a powerful magnetic field and a particular form of

stimulation is conducted (such as showing images

with a projector). Then, a series of low resolution

brain scans are taken over time. For some of these

scans the stimulus is present and for some others the

stimulus is absent. The low resolution brain images

of the two cases can then be compared in order to

see which parts of the brain were activated by the

stimulus. After the experiment has finished, the set

of images is pre-processed and analyzed.

One problem for fMRI data is that data includes

contributions from many other sources including the

heart beat, breathing and head motion artifacts,

which can cause wrong results (S.A Huettel. et al.,

2004). ICA-based methods have shown to be useful

for analyze data when this is noisy and when regions

involved in a particular task are unknown.

430

Bartés-Serrallonga M., Solé-Casals J., Adan A., Falcón C., Bargalló N. and Serra-Grabulosa J..

STATISTICAL ANALYSIS OF FUNCTIONAL MRI DATA USING INDEPENDENT COMPONENT ANALYSIS.

DOI: 10.5220/0003723504300436

In Proceedings of the International Conference on Neural Computation Theory and Applications (Special Session on Challenges in Neuroengineering-

2011), pages 430-436

ISBN: 978-989-8425-84-3

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

In an attempt to find the components extracted

from data reporting on different subjects or

paradigms and discover which were task-related and

which were noise, we applied a method based on

ICA. In this paper, we present all the steps we did

for this work and we show results obtained from real

activation fMRI experiments conducted on a group

of forty subjects.

2 MATERIALS AND METHODS

The study was performed in a 3 T MRI scanner

(Magnetom Trio Tim, Siemens Medical Systems,

Germany) at the Diagnostic Imaging Centre at

Hospital Clínic (CDIC) using the blood-oxygen

level-dependent (BOLD) fMRI signal. Whereas the

pre-processing of MR images and the regression

model were performed using SPM8 software

(SPM8, Wellcome Department of Cognitive

Neurology, London), the data analysis was carried

out using Group ICA of fMRI Toolbox (Calhoun et

al., 2001). Both pre-processing and analysis software

were run on a Matlab platform (R2009b version).

2.1 Participants

Forty right-handed healthy undergraduate students

[50% women; age range 18–25, mean (+

S.D.) 19.6

(+1.7)] were recruited from the University of

Barcelona. Subjects with chronic disorders, nervous

system disorders or history of mental illness were

excluded, as well as regular drinkers and those on

medication. All participants were non smokers and

low caffeine consumers (< 100mg/day), had

intermediate circadian typology and reported an

undisturbed sleep period of at least 6 h during the

night prior to the fMRI scan sessions. Caffeine may

affect the performance of the task (Serra-Grabulosa

et al., 2010a); Adan and Serra-Grabulosa, 2010). For

this reason the participants abstained from caffeine

intake for a minimum of 12 h and fasted for at least

8 h prior to the first fMRI session. The study was

approved by the ethics committee of Hospital Clínic

de Barcelona. Written consent was obtained from all

participants, who were financially rewarded for

taking part.

2.2 Experimental Design

The functional magnetic resonance imaging was

obtained using gradient echo sequence single-shot

echo-planar imaging, with the following parameters:

TR (repetition time): 2000 ms, TE (echo time): 40

ms, FOV (field of view): 24 x 24 cm, matrix 128 x

128 pixels, flip angle 90, slice thickness: 2 mm, gap

between sections: 0.6 mm, 36 axial slices per scan.

A total of 243 volumes were purchased, with 46

slices each.

During the acquisition of fMRI, in order to

obtain the BOLD contrast, the subjects performed a

sustained attention task (CPT-IP, Continuous

Performance Test-Identical Pairs), which is a

modification of the Cornblatt task (Cornblatt et al.,

1989) and a control task. CPT-IP task was created

with the software Presentation (Neurobehavioral

System, USA). All stimuli were presented to the

subjects through glasses specially designed for use

in the scanner.

The CPT-IP task was performed using a block

design. It started with a block of 35 seconds of

accommodation to the scanner, which had a blank

screen that the subject had to stare at. After this first

block, 9 blocks of CPT were alternated with 9

blocks of control (Figure 1). Preceding each block,

subjects received instructions for what to do in the

next block for a duration time of 5 seconds.

Figure 1: Design of the sustained attention task with

alternation between blocks.

Each of the CPT blocks had a total of 27

numbers formed by 4 digits (1 to 9, without

repeating the same figure), so that 23 of the figures

were different and 4 were repeated. The presentation

time of each number was 450 ms and the interval

between the onsets of each of the 27 consecutive

digits was 750 ms. Subjects’ task was to detect the

repeated figures and respond by pressing a button as

quickly as possible (Figure 2A). The position of the

repeated figures was randomized over the blocks

CPT. Concerning the control block, it always had

the same 4 digits (1 2 3 4) and the task of the

subjects was only to stare at it throughout the

presentation (Figure 2B).

STATISTICAL ANALYSIS OF FUNCTIONAL MRI DATA USING INDEPENDENT COMPONENT ANALYSIS

431

Figure 2: The following figure illustrates the design of the

task blocks. The top (A) exemplifies the figures presented

in the CPT blocks. In this example, you should respond

to the stimulus e3. The bottom (B) exemplifies the figures

presented in the control blocks.

2.3 Data Pre-processing

The data that comes directly out of the scanner is

very noisy. The noise is defined as any variability in

the data that is not explained by our statistical model

(Ashby, 2011), for example when a subject moves

his or her head. The magnitude of this variance is

important because it can cause some errors in the

results of the statistical analysis. If the noise is low,

it will increase the probability of discover true brain

activations related with the task.

To reduce the error variance as much as possible,

functional and structural MRI data were pre-

processed using SPM8 software (http://www.fil.ion.

ucl.ac.uk/spm/software/spm8/) as described in

(http://www.fil.ion.ucl.ac.uk /spm/doc/spm8_manual

.pdf), which aims to improve the signal noise ratio.

This includes the following steps:

1. Converting all the images from DICOM (Digital

Imaging and Communication in Medicine) format

to NIfTI (Neuroimaging Informatics Technology

Initiative) format in order to treat them with SPM8

and Group ICA of fMRI Toolbox.

2. Realigning the images to the same position

according to the coordinates of the anterior and

posterior commissure.

3. Correcting the head movements which may have

occurred in the scanner. In this way, the head

movements can cause artefacts or abrupt changes

in the intensity of the signal which can badly

corrupt fMRI data and in consequence affect the

results of the statistical analysis. The calculations

for the correction are made through

interpolations, performing 3 corrections of

rotation and 3 corrections of translation.

4. Coregistering the functional and structural

images. In this way a correspondence is achieved

point to point between the structural and the

functional images and the activations can be

interpreted.

5. Normalizing the images to minimize the huge

individual differences in the sizes and shapes of

individual brains. All brains need to be of the

same size and orientation in order to be

compared. The aim is to normalize the data into

the standard Montreal Neurological Institute

(MNI) space. This space is used worldwide, so

results are comparable with those from all other

institutes.

6. Finally, apply Gaussian transformations in order

to minimize false positives.

2.4 Implementation of the Regression

Model

After pre-processing step, we proceeded to perform

the regression model to explain brain activations. To

do this, we created a regression line where signal

changes observed in each voxel could be explained

by changes in the proposed task minimizing the

residual error (Figure 3).

2.5 Independent Component Analysis

After pre-processing and regression model creation

steps, we applied ICA analysis to the images. In the

following lines, we will explain the principles of

ICA. Independent components analysis is a

multivariate technique which is very popular and

common in the analysis of fMRI data. A good way

to understanding the basic principles of ICA is

through the typical ICA problem namely cocktail

party (Hyvärinen et al., 2000).

In this situation, some people are attending a

cocktail party speaking all at once. Assume that their

voices are recorded from different microphones

placed around the room. The resultant recordings

will be unintelligible because each microphone will

pick up some mixture of two or more people

speaking simultaneously and some background

noise. As a result, it will be very difficult to

understand even a single speaker. ICA provides an

effective method which can usually solve the

cocktail party problem separating the conversation

of every speaker.

An equivalent to this problem in fMRI is to

assume that instead of speakers, there are functional

independent neural networks that are simultaneously

active during some fMRI experiment. The aim of

ICA is to separate these simultaneous neural

networks from the global mixture as independent

components. The problem that ICA tries to solve

NCTA 2011 - International Conference on Neural Computation Theory and Applications

432

Figure 3: Regression model proposed to explain, for each

voxel of the functional MRI images, the variability in the

signal along the recorded 243 volumes. Each one of the 10

columns corresponds to one of the input variables in the

regression. The first one corresponds to the attention task

in which the subject has to respond to repeated stimuli.

The second one corresponds to the task of looking at

numbers and the third one to the task of initial rest. The

next 6 columns are the values applied to correct the head

movements in the pre-processing step. The last one

represents the error. On the right side of the table the

registered volumes are listed from 1 to 243. For each

variable, white colour indicates that this helps to explain

the variability while black colour indicates the opposite.

can be expressed in matrix notation by the following

equation:

AS (1)

where

is the (unknown) mixing matrix and S is

the (unknown) source matrix. The procedure

consists on recovering S, using only the vector X

with N observations. For that, the aim is to estimate

a weight matrix W, which should be the inverse of

A, up to scale and permutation effects, so that the

original independent signals can be recovered as:

= W

X = WAS ≈ S

(2)

To estimate the ICA model it’s necessary to

make certain assumptions and restrictions

(Hyvärinen et al., 2001):

1. The components are assumed to be statistically

independent.

2. The components must have non-gaussian

distributions.

3. For sake of simplicity, we assume that the

unknown mixing matrix is square.

4. We cannot determine the variances (energies) of

the recovered independent components.

5. We cannot determine the order of the recovered

independent components.

2.6 ICA Algorithm used

To perform the ICA analysis, as we have mentioned

before, we used the Group ICA of fMRI Toolbox.

This program has the option to make the analysis

using different algorithms, as Jade, Erica, Infomax,

Simbec, Amuse and others.

The chosen algorithm to analyze fMRI data was

Infomax because has been one of the most

commonly used algorithms for fMRI data analysis

and has proven to be quite reliable (Calhoun et al.,

2004).

3 RESULTS

3.1 Selection of the Independent

Components

After ICA analysis we selected some of the

components in order to evaluate results. For that, we

did a multiple regression and a statistic correlation

with every paradigm. We excluded the components

that had a p-value greater than 0.01, and the ones

which were associated to noise. Therefore we

selected 3 components for the CPT task and 3

components for the control task.

3.2 Obtention of the Areas of Interest

After the selection of the independent components,

we performed a T – test with all the subjects and all

the components. We also performed a ‘multiple

regression’ SPM8 analysis to establish the

relationship between CPT-IP-related activations.

The fMRI results were interpreted only if they

attained both a voxelwise threshold p<0.05

(corrected) (cluster extent (k) = 10voxels). The

anatomical location of the activated brain areas was

determined by the Montreal Neurological Institute

(MNI) coordinates. Anatomical labels were given on

the basis of anatomical parcellation developed by

(Tzourio-Mazoyer et al., 2002).

STATISTICAL ANALYSIS OF FUNCTIONAL MRI DATA USING INDEPENDENT COMPONENT ANALYSIS

433

3.3 fMRI Results

Activations found in the CPT task were located (see

Table 1 and Figure 4) bilaterally in frontal lobe (BAs

6, 8, right 9, 10, 11, 24, 32, 44, 45, 46, 47), parietal

(BAs 7, 23, 31, 40), temporal (BAs 21, 22, 34, right

37) and occipital (BAs 18, 19).

The control task showed a pattern of bilateral

activation (see Table 2 and Figure 5) in frontal lobe

(BAs 4, left 6, 8, 9, 10, 11, 24, 32), parietal (BAs

right 2, left 3, right 5, 7, 23, 31, 39, 40), temporal

(BAs 20, 21, 28, 34, 35, 37, 38) and occipital (BAs

17, 18).

4 DISCUSSION

The aim of our study was to analyze fMRI data from

a stimulation paradigm using ICA, and compare the

obtained results with previous ones done in other

study (Serra-Grabulosa et al., 2010b) which

analyzed the same data using general linear

modelling (GLM).

In general terms, obtained results follow a

similar pattern as previous analysis reported in

(Serra-Grabulosa et al., 2010) but with more active

regions. In the following paragraph we will

comment these new activations.

As in the GLM case, ICA analysis of the CPT

task indicated that the used paradigm activates a

network in frontal, parietal and occipital areas. In

addition, the new results showed activations in the

temporal area. The frontal activation obtained was

bilateral and the new included areas were frontal eye

fields (BA 8), dorsolateral prefrontal cortex (right

BA 9), ventral anterior cingulate cortex (BA 24) and

inferior prefrontal gyrus (BA 47). Frontal eye fields

are believed to play an important role in the control

of eye movements and in the management of

uncertainty (Volz et al., 2005) which could be

present during the CPT task. BA 9 is part of

dorsolateral prefrontal cortex and it’s involved in

functions such as working memory, integration of

sensory mnemonic information and the regulation of

intellectual function and action. These functions

were necessary in the CPT task in order to remember

the numbers, to compare them and to decide the

correct answer. BA 24 is part of the anterior

cingulate cortex and many studies attribute functions

such as error detection, anticipation of tasks,

attention (Weissman et al., 2005), motivation, and

modulation of emotional responses to the ACC

(Bush et al., 2000; Posner et al., 1998; Nieuwenhuis

et al., 2001). Thus this area could contribute to

maintain the attention during the task and detecting

the equal numbers. BA 47 has been implicated in the

processing of syntax in spoken and signed

languages. Therefore, this zone could be related to

the processing of the numbers during the task.

Bilateral parietal activations were also found in

the CPT task. These are in the posterior cingulate

cortex, which is associated with Brodmann areas 23

and 31. Imaging studies indicate a prominent role for

the posterior cingulate cortex in pain and episodic

memory retrieval (Nielsen et al., 2005). Thus, this

part of the cortex could contribute to recover the

digits from memory during the task. BA 40 and

more exactly its supramarginal gyrus part, is

involved in reading, both regarding meaning and

phonology (Stoeckel C. et al., 2009). In our case it

may be related with the number recognition.

Another cluster of activation related to the CPT

task, and not found in the previous study, was found

in temporal areas. BA 21 has been connected with

processes as different as observation of motion,

recognition of known faces and accessing word

meaning while reading. BA 22 is an important

region for the processing of speech so that it can be

understood as language. BA 37 includes functions as

face and body recognition, number recognition and

processing of colour information. These regions

could be related to the recognition and the numbers

meaning when were shown. BA 34 is a part of the

entorhinal area which is the main interface between

the hippocampus and neocortex. The entorhinal

cortex (EC)-hippocampus system plays an important

role in autobiographical / declarative / episodic

memories and in particular in spatial memories

including memory formation, memory consolidation

and memory optimization in sleep. Therefore this

area could contribute to processing the numbers

during verbal working memory.

Comparing with GLM, ICA analysis of the control

task also indicated activity in angular gyrus,

posterior cingulate gyrus, frontal gyrus and inferior

and medial temporal gyrus. In addition, ICA results

showed activations in primary motor cortex,

premotor cortex, primary somatosensory cortex,

somatosensory association cortex, perirhinal cortex

and temporopolar area. As in the previous analysis,

the control task showed activations in different brain

areas which were not activated in the CPT task and

probably could reflect an inhibition of processes that

could interfere with the correct execution of the task,

as external and internal monitoring (Gusnard and

Raichle, 2001). This deactivation could optimize

performance in high attentional demanding tasks

(McKiernan et al., 2003).

NCTA 2011 - International Conference on Neural Computation Theory and Applications

434

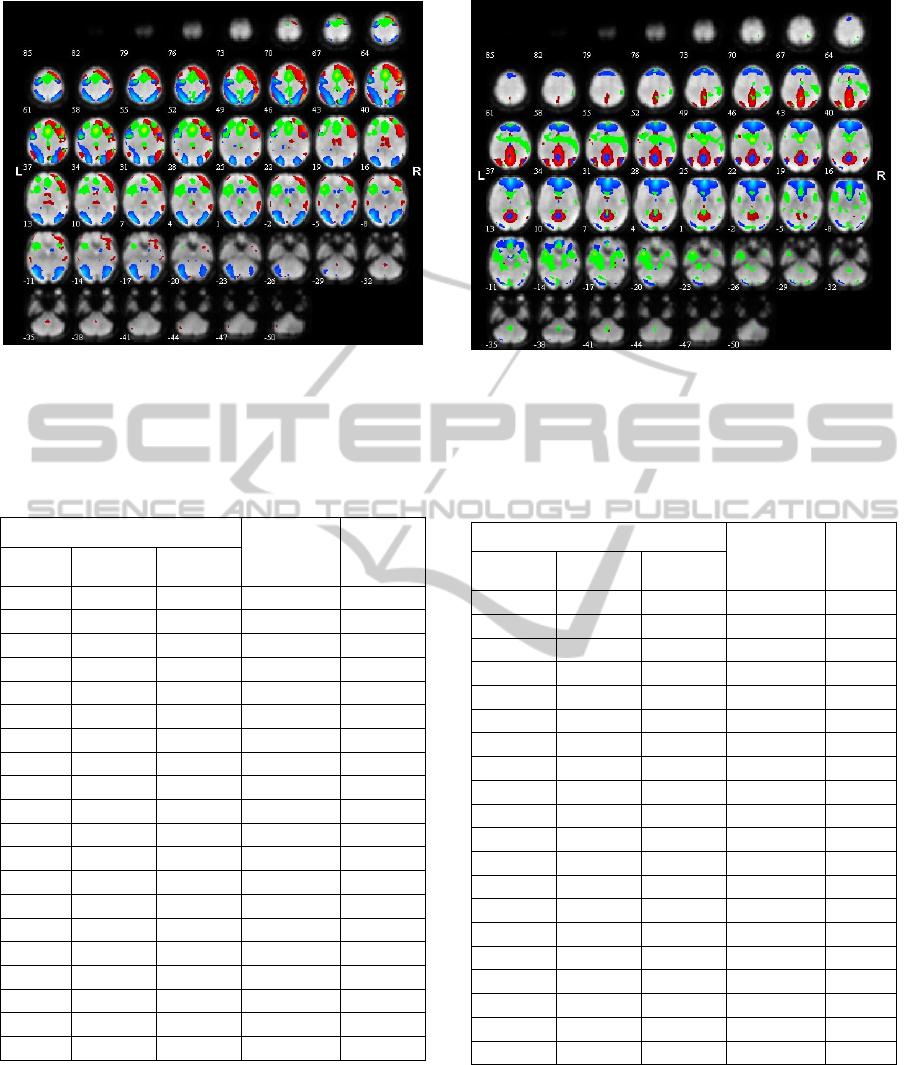
Figure 4: This figure shows the activations found on

the CPT task. Each colour represents the active region of a

different component.

Table 1: Coordinates (x, y, and z) of the areas of

significance, level of significance (T-Score) and

localization of the voxel (BA) for CPT task.

Coordinates of voxels

T-Score BA

x y z

3 11 49 32.64 6

-51 20 40 11.10 8

42 53 4 22.94 10

48 14 28 23.09 9

0 29 22 29.08 24

6 23 31 31.43 32

-45 12 20 6.18 44

60 14 19 11.70 45

48 32 25 23.71 46

36 23 -5 10.88 47

24 -67 49 25.91 7

0 -25 31 8.24 23

-24 -76 28 20.94 31

-48 -61 43 14.00 40

63 -31 -5 16.72 21

-48 8 -2 16.68 22

9 5 -11 12.15 34

57 -43 -5 10.18 37

-30 -88 4 25.17 18

39 -82 -5 22.88 19

5 CONCLUSIONS

After the analysis ICA has demonstrated to be a

technique with a great potential. Comparing with

GLM-based approaches ICA is able to separate

statistical independent components and identify

Figure 5: This figure shows the activations found on the

control task. Each colour represents the active region of a

different component.

Table 2: Coordinates (x, y, and z) of the areas of

significance, level of significance (T-Score) and

localization of the voxel (BA) for control task.

Coordinates of voxels

T-Score BA

x y z

-33 -22 58 7.98 4

-24 -19 64 7.70 6

-21 38 46 10.07 8

9 53 37 8.64 9

3 53 -5 42.53 10

0 41 -14 9.83 11

0 26 19 10.92 24

-3 44 -2 43.77 32

33 -37 61 6.60 2

-12 -37 67 6.45 3

3 -40 64 7.50 5

15 -52 49 7.44 7

3 -58 16 28.66 23

-6 -64 22 37.85 31

48 -64 28 10.84 39

60 -25 31 10.74 40

-42 -25 13 6.67 41

-57 -7 -20 8.68 20

57 -13 -17 8.94 21

-21 -16 -17 7.81 28

more networks than GLM. The main inconvenience

we observe with ICA is that in some cases it might

identify a large number of components, while only a

few are related with the task. To find those related

components can be a challenge. Therefore it’s

important to estimate an appropriate number of

components in order to better separate the real

STATISTICAL ANALYSIS OF FUNCTIONAL MRI DATA USING INDEPENDENT COMPONENT ANALYSIS

435

activations from noise. Despite these difficulties,

ICA works well and separates noise from real

activations allowing extracting the desired signals.

ACKNOWLEDGEMENTS

This work has been partially supported by the

Secretaria d’Universitats i Recerca of the

Departament d’Economia i Coneixement of the

Generalitat de Catalunya under the grant 2010BE1-

00772 to Dr. Jordi Solé-Casals; by the University of

Vic under de grant R0904; and by grants of the

Ministerio de Educación y Ciencia of the Spanish

Government (SEJ2005-08704) and the Departament

d’Innovació, Universitats i Empresa of the

Generalitat de Catalunya /2009BE-2 00239) to Dr.

Josep M Serra-Grabulosa.

REFERENCES

Adan A, Serra-Grabulosa JM ., 2010. Effects of caffeine

and glucose, alone and combined, on cognitive

performance. Human Psychopharmacology clinical

and experimental, 25 (4), 310 – 317.

Ashby, F., 2011. Statistical analysis of fMRI Data.

Cambridge, MA: MIT Press

Bush G., Luu P., Posner M. I., 2000. Cognitive and

emotional influences in anterior cingulate cortex.

Trends Cogn Sci., 4 (6), 215 – 222.

Calhoun, V. D., Adali, T., Pearlson, G. D. and Pekar, J. J.,

2001,”A Method forMaking Group Inferences From

Functional MRI Data Using Independent Component

Analysis”, HBM, 14, 140 – 151.

Calhoun, V. D., Adali, T., Pearlson, G. D., 2004,

”Independent component analysis applied to fMRI

data: a generative model for validating results”, J.

VLSI Signal Process, 37, 281 – 291.

Cornblatt, B. A., Lezenweger, M. F., Erlenmeyer-Kimling,

L., 1989. The Continuous Performance Test, Identical

Pairs Version: II. Contrasting attentional profiles in

schizophrenic and depressed patients. Psychiatry

Research, 29, 65 – 85.

Gusnard D. A., Raichle M. E., 2001. Searching for a

baseline: Functional imaging and the resting human

brain. Nature Neuroscience Reviews, 2, 685 – 694.

D’Esposito, M., Zarahn, E., Aguirre, G. K., 1999. Event-

Related functional MRI: implications for cognitive

Psychology. Psychological Bulletin, 125, 155 – 64.

Hyvärinen, A., Oja E., 2000. Independent component

analysis: Algorithms and applications. Neural

Networks, 13, 411 – 430.

Hyvärinen A., Oja E., Karhunen J., 2001. Independent

component analysis, John Wiley & Sons.

McKiernan K. A., Kaufman J. N., Kucera-Thompson J.,

Binder J. R., 2003. A parametric manipulation of

factors affecting task-induced deactivation in

functional neuroimaging. Journal of Cognitive

Neuroscience, 15, 394 – 408.

Nielsen F. A., Balslev D., Hansen L. K., 2005. Mining the

posterior cingulate: segregation between memory and

pain components. Neuroimage, 27 (3), 520 – 532.

Nieuwenhuis S., Ridderinkhof K. R., Blom J., Band G.P.,

Kok A., 2001. Error-related brain potentials are

differentially related to awareness of response errors:

evidence from an antisaccade task. Psychophysiology,

38 (5), 752 – 60.

Posner M. I., DiGirolamo G. J., 1998. Executive attention:

Conflict, target detection, and cognitive control. In

Parasuraman R. The attentive brain. Cambridge, Mass:

MIT Press.

Scott A. Huettel, Allen W. Song, and Gregory McCarthy.,

2004. Functional magnetic resonance imaging.

Sunderland, MA: Sinauer Associates

Serra-Grabulosa J. M, Adan A, Falcon C , Bargallo N,

2010a Glucose and caffeine effects on sustained

attention: an exploratory fMRI study. Human

Psychopharmacology clinical and experimental 25 (7-

8), 543 – 552

Serra-Grabulosa J. M., Adan A., Falcón C., Bargalló N.,

Solé-Casals J., 2010b. Cerebral correlates of the

continous performance test-identical pairs version: An

fMRI study. In Proceedings of the Third Internationa

Conference on Bio-inspired Systems and Signal

Processing – BIOSIGNALS.

Stoeckel C., Gough .P. M., Watkins K. E., Devlin J. T.,

2009. Supramarginal gyrus involvement in visual

word recognition. Cortex, 45 (9),1091 – 1096.

Tzourio-Mazoyer N, Landeau B, Papathanassiou D,

Crivello F, Etard O, Delcroix N. et al. 2002.

Automated anatomical labeling of activations in SPM

using a macroscopic anatomical parcellation of the

MNI MRI single-subject brain. Neuroimage 15, 273 –

289.

Volz K. G., Schubotz R. I., von Cramon D. Y., 2005.

Variants of uncertainty in decision-making and their

neural correlates. Brain Res. Bull, 67 (5), 403 – 12.

Weissman D. H., Gopalakrishnan A., Hazlett C. J,

Woldorff M. G., 2005. Dorsal Anterior Cingulate

Cortex Resolves Conflict from Distracting Stimuli by

Boosting Attention toward Relevant Events. Cerebral

Cortex, 15, 229 – 237.

NCTA 2011 - International Conference on Neural Computation Theory and Applications

436