EVOLUTIONARY STRATEGIES FOR THE ACADEMIC

CURRICULUM BALANCED PROBLEM

Lorna V. Rosas-Tellez

, Jose L. Martínez-Flores

and Vittorio Zanella-Palacios

Universidad Popular Autónoma del Estado de Puebla, Information Technologies Department

13 Poniente 1927 Col. Santiago, Puebla Pue, México

Universidad Popular Autónoma del Estado de Puebla, Interdisciplinary Center for Postgraduate Studies,

Research and Consulting, 21 sur 1103 Col. Santiago, Puebla Pue, México

Keywords: Evolutionary strategies, Academic curriculum balanced problem.

Abstract: The Balanced Academic Curriculum Problem (BACP) is considered an optimization problem, which consist

in the assignment of courses in periods that form an academic curriculum so that the prerequisites are

satisfied and the courses load is balanced for students. The BACP is a constraint satisfaction problem

classified as NP- Hard. In this paper we present the solution to a modified problem BACP where the loads

can be the equals or different for each one of the periods and is allowed to have some courses in a specific

period. This problem is modeled as an integer programming problem, for which had been obtained solutions

for some of their instances with HyperLingo but not for all. Therefore, we propose the use of evolutionary

strategies for its solution. The results obtained for the instances of the modified and the original BACP,

proposed in the CSPLib, showing that with the use of evolutionary strategies is possible to find the solution

for instances of the problem that with the formal method is not possible to find.

1 INTRODUCTION

A curriculum is formed by a set of courses, these

courses have assigned a number of credits that

represent the effort in hours per week that the

student requires to follow the courses successfully,

for parents or tutors and the institution represents the

economic cost of this course. The academic load is

the sum of the credits of the courses in a given

period.

Therefore correct planning of the curriculum,

result in benefit of the institution and all the

involved: To the institutions favors the

departmentalization and the resulting cost savings, to

students in a good load distribution because this

represents the academic effort that they require

invest, the parent or tutors a good distribution of the

credits allow planning financial efforts.

Balanced Academic Curriculum Program

(BACP) consists in to assign courses to the periods

that are part of curriculum so that prerequisites are

satisfied and the credits load is balanced. The BACP

problem belongs to the class of problems CSP

(Constraint Satisfaction Problems), as this is a

decisional optimization problem is classified as NP-

Hard (Salazar, 2001).

The BACP problem was introduced by Castro

and Manzano (Castro, 2001) with three test cases

called BACP8, BACP10 and BACP12 included in

CSPLib and they have been used to test models

proposed by other researchers.

The model proposed by Castro and Manzano

uses the following integer programming model:

Parameters

m : Number of courses

n : Number of periods



: Number of course credits i; i =1, …, m



: Minimum academic load per period



: Maximum academic load per period



: Minimum amount of courses per period



: Maximum amount of courses per period

Decision Variables

: period of course i, i =1, …, m, x

 [1,…,n]

: load academic of course i, i =1, …, m

Objective Function

),..1,(

njjxcMaxcMin







(1)

534

V. Rosas-Tellez L., L. Martínez-Flores J. and Zanella-Palacios V..

EVOLUTIONARY STRATEGIES FOR THE ACADEMIC CURRICULUM BALANCED PROBLEM.

DOI: 10.5220/0003723805340538

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (FEC-2011), pages 534-538

ISBN: 978-989-8425-83-6

 2011 SCITEPRESS (Science and Technology Publications, Lda.)

Constraints

If the course b has the course a as prerequisite then:

< x









jxc

(2)









k 1

(3)

Recent works have tried to solve the problem using

genetic algorithms and constraint propagation

(Lambert, 2006), with local search techniques (Di

Gaspero, 2008), with formal methods (HyperLingo)

for the integer programming problems (Aguilar-

Solis, 2008), with multiple optimization, using

genetic algorithm of local search (Castro, 2009). All

these studies have found the optimal for the three

test cases included in CSPLib and in some cases also

for the curriculums of their universities.

In (Aguilar-Solis, 2008) was proposed a

modified BACP problem where it is considered

constraints of academic load and total of courses

within a specific range per period, i.e., not

necessarily all periods will have the same ranges for

their academic loads and number of courses; also

add the restriction of to locate a course in a given

period. This problem was modeled as an integer

programming problem, and is reported to find

optimum solutions, using a formal method, for some

of its instances but not for all of them and solutions

for the three instances included in CSPLib.

In this paper we solve the modified BACP

problem using evolutionary strategies to find

solutions to the instances that formal method could

not to solve.

2 MODEL FORMULATION FOR

BACP MODIFIED

In the model of interest proposed in (Aguilar-Solis,

2008) is considered to modify two constraints of the

base formulation, the first one is to make flexible the

course load per period and the second one is to make

flexible the number of courses per period, i.e., that

we can place different limits on course load and

number of courses for each period. It also adds a

restriction which allows the location of the courses

in a specific period.

Parameters

Nta : Number of courses

Ntp : Number of academic periods

crd

: Number of course credits i=1,…, Nta

mca

: Minimum academic load allowed per

period

Mca

: Maximum academic load allowed per

period

mna

: Minimum number of courses per period

Mna

: Maximum number of courses per period

c : Course it is desirable to locate between

certain periods.

mpc

: Minimum period of location of the course

Mpc

: Maximum period of location of the

course

: Academic load

NtpjxcrdC

Nta

ijij

,...,1*







(4)

Decision Variables

: Academic load for the period j=1,…, Ntp

Cmx : Maximum course load

Objective Function

objetive

= Min { Cmx }

where Cmx = Max { c

, c

, …, c

Ntp

}

Constraints

The load of the period j must be within the allowable

range.

NtpjMcaCmca

jji

,...,1



(5)

The number of courses of the period must be within

the allowable range.

NtpjMnaxmna

Nta

ijj

,...,1







(6)

If the course b has the course a as prerequisite the

course

Ntpjxx

arbj

,...,2









(7)

Convenient location for the course c

1





Mpc

mpvj

(8)

3 EVOLUTIONARY

STRATEGIES

Evolutionary Strategies are optimization algorithms

based on Darwin's theory of evolution, which states

1 if course i is assigned to period j

0 otherwise

EVOLUTIONARY STRATEGIES FOR THE ACADEMIC CURRICULUM BALANCED PROBLEM

535

that only those individuals best adapted to their

environment survive and reproduce. The procedure

starts by choosing a random number of possible

solutions in the search space to generate an initial

population. Based on a fitness function evaluated for

each possible solution, choose the best members of

the population to take part in reproduction, this

process is called selection. With the best members of

the population selected genetic operations are

carried out with the idea that new promising

individuals will be evolved from their ancestors to

produce an improved population. The genetic

operations that generally are used are crossover and

mutation, which in evolutionary strategies is the

most important operation. The crossover is the

combination of information from two or more

individuals and mutation is the alteration of the

information of a single individual (Michalewicz,

1999). There are several types of evolutionary

strategies depending on the size of the population

and how the individuals are replaced in the

population prior to generating the new population. In

our case we use an evolutionary strategy EE-(1+3),

i.e., there is an initial population of a single

individual and from this individual will generate 3

new individuals by mutation. Of these 4 individuals

the best is choosing for the next population.

Evolutionary strategies were used, at least

initially, to optimization problems of real functions,

but are possible to use it successfully in other

domains. In this paper we use evolutionary strategies

in populations where individuals are vectors.

One element of the population is represented by

a vector, where the position indicates the course and

content of each position indicates the period to

which it was assigned, as shown in figure 1.

0 1 2 3 4 5 59 60 61

1 1 3 1 2 2 9 9 0

Figure 1: Element of the Population.

In our case we used a population with a single

individual so that the only operation performed is

mutation, which consists in changing the period of a

course of the curriculum that meets the prerequisites

and restrictions of preference period.

We can consider that a balanced curriculum

should have a uniform distribution of all the credits

that make up the curriculum, so the fitness function

used is the sum of the absolute error, which is

calculated using the following formula.







Ntp

PChFitness

)(

(9)

Where C

is the academic load of the period k

calculated with the formula (4) and P is the average

number of credits per period

NtpCP

Ntp





(10)

The initial population consists of the curriculum that

we want to balance, this is a feasible solution.

Once that we have the first element of the

population three new elements are generated through

mutation. As the mutation is the random change of

the value of a single element within the vector,

randomly are chosen a course to be changed and the

period where it will change.

Given the course and the period, are validated

the restrictions prerequisites, load, course and time

preference, if they are satisfied, the change is made,

otherwise are selected randomly another course and

period and redo the validation. This continues until

to find the pair course - period that meets with the

restrictions. This will generate 3 new individuals

from the individual in the present population. The

four individuals are evaluated by the fitness function

(formula 9) and the best is selected for the next

generation.

When is detected that a local optimum has been

reached, a change in the process of mutation is

made. Now, the mutation will change two elements

of the vector, that is, now going to get the periods

with more load and less load and will try to

exchange two courses randomly between these two

periods.

Having the two courses which will be

exchanged, are evaluated the restrictions of

prerequisite , load, course and period preference, if

the exchange can be given a new individual is

generated in otherwise the mutation is not done, the

minimum period is marked as ineligible for the next

selection and is cleared until that an improvement

occurs.

4 RESULTS

The tests were carried out for the three base cases

included in CSPLib and the cases proposed by

(Aguilar-Solis, 2008) for which no solution could be

found.

4.1 Base Cases

The base cases included in CSPLib are: BACP8,

BACP10 and BACP12, whose features are shown in

FEC 2011 - Special Session on Future of Evolutionary Computation

536

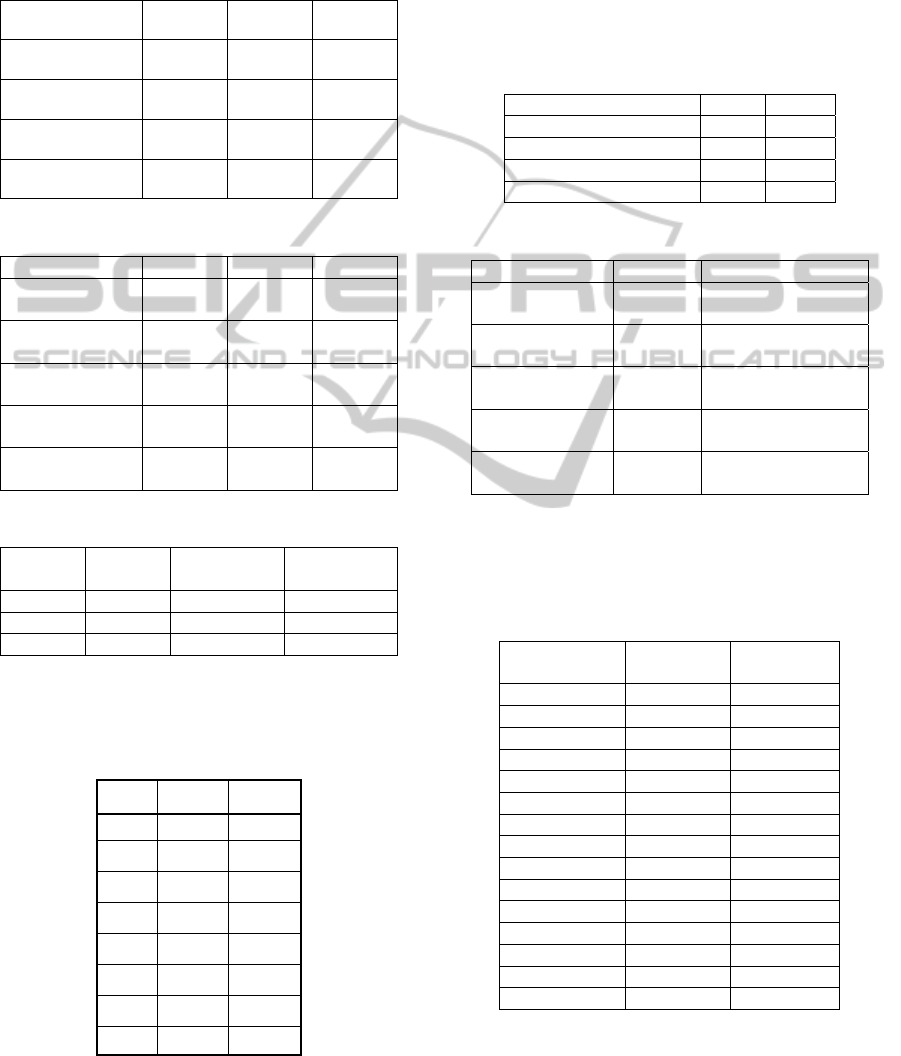
tables 1 and 2.

Table 3 shows the results obtained with the

proposed algorithm; in all cases the optimum was

reached.

Table 1: General features of curriculums.

Code BACP8 BACP10 BACP12

# Total Courses 46 42 66

# Total credits 133 134 204

#Total Academic

erio

8 10 12

#Relation

Prere

uisite

33 34 65

Table 2: Additional features of the curriculums.

Code BACP8 BACP10 BACP12

Min. Courses

/period

2 2 2

Max. Courses /

period

10 10 10

Min Load/

period

10 10 10

Max Load/

period

24 24 24

#Courses with

location

0 0 0

Table 3: Results summary.

Code Optimum

Average

Iterations

Average

time (min.)

BACP 8

17 57.6 1.5

BACP 10

14 87.7 1.7

BACP 12

17 162.0 2.5

The academic load per period obtained by the

algorithm is shown in table 4.

Table 4: Solution found for BACP 8.

Period Load Courses

1 17 7

2 17 5

3 17 5

4 17 6

5 17 6

6 17 6

7 15 5

8 16 6

4.2 Proposed Cases

The cases not included in library CSPLib used to test

this algorithm are taken from (Aguilar-Solis, 2008),

the first is one for which could not always find the

optimal and the second is where the optimum never

was found. The features of these two problems are

shown in tables 5 y 6.

Table 5: General features of curriculums.

Code

Ici-06 Ind-06

# Total Courses 61 61

# Total credits 488 376

#Total Academic period 9 9

#Relation Prerequisite 48 47

Table 6: Additional features of the curriculums.

Code Ici-06 Ind-06

Min. Courses

/period

5 4, 4, 4, 4, 4, 4, 4, 4,

Max. Courses/

period

8 9, 9, 9, 9, 9, 9, 9, 9,

Min Load/

period

20 20, 20, 20, 20, 20,

20, 20, 20, 15

Max Load/

period

60 60, 60, 60, 60, 60,

60, 60, 60, 40

#Courses with

location

15 21

In tables 7 and 8 is showing the courses that have

preference of location in each of the curriculums,

Ici-06 and Ind-06 respectively.

Table 7: Preference of location Ici-06.

Course Code Minimum

Period

Maximum

Period

C07001 7 9

C07002 7 9

C07003 7 9

CIV200 1 2

CIV400 6 9

CIV401 8 9

CIV403 6 9

MAT005 1 5

MAT006 1 5

MAT008 1 5

MAT009 1 5

OI103101 1 4

OI103102 1 4

OI103103 1 4

OI103104 1 4

EVOLUTIONARY STRATEGIES FOR THE ACADEMIC CURRICULUM BALANCED PROBLEM

537

Table 8: Preference of location Ind-06.

Course Code Minimum

Period

Maximum

Period

C12001 7 9

C12002 7 9

C12003 7 9

C12004 8 9

FHU001 1 6

FHU002 1 6

FHU003 1 6

IND100 1 2

IND208 4 6

IND212 4 6

IND214 6 8

IND400 7 9

LPCI 1 6

LPCII 1 6

OH25001 1 6

OI103101 1 6

OI103102 1 6

OI103103 1 6

OI103104 1 6

SSC001 5 9

SSP002 5 9

Table 9 shows the results obtained with the

algorithm; in all cases the optimum was reached.

Table 9: Results summary.

Code Optimum

Average

Iterations

Average

time (min.)

Ici-06

55 57.6 16

Ind-06

44 87.7 19.7

The academic load per period obtained by the

algorithm is shown in Table 10.

Table 10: Solution found for Ici-06.

Period Load Courses

1 54 7

2 54 6

3 54 6

4 54 7

5 55 6

6 55 6

7 54 8

8 54 7

9 54 8

5 CONCLUSIONS

In this paper we present the solution, using

evolutionary strategies, for a modified Balanced

Academic Curriculum Problem, where the load for

each period can be equal or different and is allowed

to have some courses in a specific period. In a

previous work is showed that is possible to find

solutions with HyperLingo for some of the instances

of the problem, but not for all of them. However by

the results obtained was proved that the use of

evolutionary strategies helps to find solutions to the

problems that could not be resolved with the formal

method.

REFERENCES

Aguilar-Solís J. A., Un modelo basado en optimización

para balancear planes de estudio en Instituciones de

Educación Superior, PhD Thesis, Puebla: UPAEP,

2008.

Castro, C., Crawford, B., Monfroy, E., A Genetic Local

Search Algorithm for the Multiple Optimisation of the

Balanced Academic Curriculum Problem, In

Proceedings of MCDM, pages 824-832, Berlin:

Springer-Verlag, 2009.

Castro, C., Manzano, S., Variable and value ordering

when solving balanced academic curriculum problem,

Proc. of the ERCIM Working Group on Constraints,

2001.

Di Gaspero, L., Schaerf, A., Hybrid Local Search

Techniques for the Generalized Balanced Academic

Curriculum, In Proceedings of HM, pages 146-157,

Berlin: Springer-Verlag, 2008.

Lambert, T., Castro, C., Monfroy, E., Saubion, F., Solving

the Balanced Academic Curriculum Problem with an

Hybridization of Genetic Algorithm an Constraint

Propagation, In Proceedings of ICAISC, pages 410-

419, Berlin: Springer-Verlag, 2006.

Michalewicz, Z., Genetic Algorithms + Data Structures =

Evolution Programs, Berlin: Springer-Verlag, 1999.

Salazar, J., Programación matemática, Madrid: Diaz de

Santos, 2001.

FEC 2011 - Special Session on Future of Evolutionary Computation

538