
CONCATENATION METHOD FOR HIGH-TEMPORAL
RESOLUTION SSVEP-BCI
Yohei Tomita
1
, Antoine Gaume
1
, Hovagim Bakardjian
2
, Monique Maurice
2,3
, Andrzej Cichocki
2
,
Yoko Yamaguchi
3
, G´erard Dreyfus
1
and Franc¸ois-Benoˆıt Vialatte
1,2
1
SIGMA Laboratory,
´
Ecole Sup´erieure de Physique et de Chimie Industrielles de la Ville de Paris
10 Rue Vauquelin 75231, Paris Cedex 05, France
2
Riken BSI, Laboratory ABSP, 2-1 Hirosawa, Wako-shi, Saitama-Ken, 351-0128, Japan
3
Riken BSI, Laboratory DEI, 2-1 Hirosawa, Wako-shi, Saitama-Ken, 351-0128, Japan
Keywords:
Concatenation method, Heisenberg-Gabor uncertainty principle, High-temporal resolution BCI, SSVEP,
EEG.
Abstract:
Electroencephalographic (EEG) signals are generally non-stationary, however, nearly stationary brain re-
sponses, such as steady-state visually evoked potentials (SSVEP), can be recorded in response to repeti-
tive stimuli. Although Fourier transform has precise resolution with long time windows (5 or 10 s for in-
stance) to extract SSVEP response (1-100 Hz ranges), its resolution with shorter windows decreases due to the
Heisenberg-Gabor uncertainty principle. Therefore, it is not easy to extract evoked responses such as SSVEP
within short EEG epochs. This limits the information transfer rate of SSVEP-based brain-computer interfaces.
In order to circumvent this limitation, we concatenate EEG signals recorded simultaneously from different
channels, and we Fourier analyze the resulting sequence. From this constructed signal, high frequency res-
olution can be obtained with time epochs as small as only 1 s, which improves SSVEPs classification. This
method may be effective for high-speed brain computer interfaces (BCI).
1 INTRODUCTION
Brain computer interfaces (BCI) are alternative meth-
ods to the normal outputs of the brain via the nerve-
muscle system (Birbaumer, 2006). The purpose of
BCI is to detect physiological signals from the brain
and translate them into a control signal for an external
device. It has been developed with surface electroen-
cephalograms (EEG), electrocorticograms (ECoG),
and implanted electrodes. Among them, surface EEG
has many advantages: it is non-invasive, technically
less demanding, and evoked responses are fast (within
the millisecond range). Especially, short response
times of EEG could enable users to control an ex-
ternal device almost in real-time (Sanei and Cham-
bers, 2007; Bashashati et al., 2007; Lotte et al.,
2007). However, nowadays the available BCI systems
are generally constrained to execute commands using
epochs of more than 3 s. For instance, in BCI word
processing systems, it takes more than 3 s to type each
letter. Therefore, being able to detect BCI commands
with shorter time epochs (about 1 s) is a crucial prob-
lem.
EEG signals are known to be non-stationary
1
(see
for instance (Kawabata, 1973)). However, in steady-
state visually evoked potentials (SSVEP), EEG fea-
tures at the stimulation frequency and its harmonics
are nearly stationary (Vialatte et al., 2010). When
subjects focus attention on flickering lights with con-
stant frequencies, steady-state brain activity appears,
predominantly in the occipital cortex, and propagates
to other brain areas. These responses are better ob-
served in the frequency, or time-frequency domains.
Therefore, to detect these features, frequency or time-
frequency analysis methods are applied, such as clas-
sical Fourier transform or wavelet transform (Quiroga
et al., 2001; Vialatte et al., 2008; Bin et al., 2009).
Moreover there are other methods such as empiri-
cal mode decomposition for instantaneous frequency
(Huang et al., 1998).
To detect these SSVEPs with high temporal res-
olution, one generally uses short EEG epochs to
1
Their statistical properties evolve with time
444
Tomita Y., Gaume A., Bakardjian H., Maurice M., Cichocki A., Yamaguchi Y., Dreyfus G. and Maurice F..
CONCATENATION METHOD FOR HIGH-TEMPORAL RESOLUTION SSVEP-BCI .
DOI: 10.5220/0003724404440452
In Proceedings of the International Conference on Neural Computation Theory and Applications (Special Session on Challenges in Neuroengineering-
2011), pages 444-452
ISBN: 978-989-8425-84-3
Copyright
c
2011 SCITEPRESS (Science and Technology Publications, Lda.)

compute Fourier transforms. However, due to the
Heisenberg-Gabor uncertainty principle, high fre-
quency resolution cannot be obtained by Fourier
transforming short signals: the shorter the window
length, the lower the frequency resolution. Further-
more, when using short epochs, EEG becomes nearly
stationary. Therefore for short epochs the Fourier rep-
resentation of SSVEP and non-SSVEP activity are of
comparable amplitudes, hence SSVEP peak is diffi-
cult to be detected. As a result, SSVEP cannot be de-
tected reliably with short windows (a minimum of 3 s
is usually required). To circumvent this limitation, we
propose a concatenation method: EEG epochs mea-
sured simultaneously from different channels are con-
catenated, in order to generate an artificially longer
epoch that can be analyzed with a better frequency
resolution. The details of this method are described
in the following sections. We then demonstrate this
method on a real SSVEP classification task.
The organization of the paper is as follows. Sec-
tion 2 details the procedure of the concatenation
method. In section 3, an EEG electrode placement
and the experimental procedure are presented. Re-
sults, discussions and conclusions are in sections 4, 5,
and 6, respectively.
2 CONCATENATION METHOD
In this section, the concatenation method is detailed.
Firstly, the non-stationarity of EEG is shown with dif-
ferent sizes of time epoch. Secondly, we propose the
concatenation method to circumvent this problem.
2.1 Non-stationarity of EEG
EEGs are considered non-stationary. When using fre-
quency analysis methods such as the Fourier trans-
form and the wavelet transform, rhythmic compo-
nents of the EEG (such as the theta or the alpha wave)
are extracted for decomposing a signal into a set of
frequency components. However, the Fourier trans-
form relies on the assumption that the analyzed sig-
nal is strictly stationary, otherwise, the resulting spec-
trum will make little physical sense. Therefore, when
using long time epochs, these non-stationary compo-
nents have limited impact on the Fourier spectrum.
On the other hand, when using short time windows,
EEG frequency components become nearly station-
ary, with higher resulting Fourier amplitudes.
SSVEPs are nearly stationary evoked responses,
much more stable than classical EEG signals. They
have very narrow-band responses, with precise spec-
tral properties (an SSVEP response at 10 Hz exhibit
0 2 4 6 8 10
−5
0
5
Oz signal
Amp.
Time (s)
5 10 15 20 25 30 35 40
0
500
Fourier power with 10 s window
Frequency (Hz)
5 10 15 20 25 30 35 40
0
500
Fourier power with 5 s window
Frequency (Hz)
5 10 15 20 25 30 35 40
0
200
400
Fourier power with 2 s window
Frequency (Hz)
5 10 15 20 25 30 35 40
0
100
200
Fourier power with 1 s window
Frequency (Hz)
Figure 1: 10 Hz SSVEP responses: Top, Oz signal; Bot-
tom four, Fourier power with different time windows of [0,
time] (time∈[10, 5, 2, 1]). With the shorter windows, it
shows lower time resolution and the peak is lower at the
fundamental and harmonic frequencies.
a clear peak at 10 Hz, with a width below 1 Hz).
These responses can be observed in a frequency do-
main shown in Fig. 1.
Frequencies of EEG signal were calculated by
Fourier transform with different sizes of Hanning
window function. The spectrum obtained with a 10
s time window exhibits sharp peak nears 10, 20, and
30 Hz. Conversely, the spectrum obtained with a 1
s time window exhibits lower peaks at these frequen-
cies, and it has a lower frequency resolution. Notably,
Fourier powers at frequencies surrounding stimulus
frequency and its harmonics are higher when the time
epoch is shorter. This is because, for long EEG
epochs, the non-stationary components of EEG sig-
nals except the stimulus frequency have less impact
on the Fourier spectrum. Thus, sharper and clearer
SSVEP peaks can be obtained. On the other hand, for
short EEG epochs, it has lower spectral amplitudes,
which blurs out the SSVEP peak, which is further-
more distorted by the low frequency resolution.
2.2 Concepts of Concatenating
The concatenation method we propose is a way to im-
prove artificially the frequency resolution while using
very short EEG epochs. The details of this method are
as follows.
Let x
i
be the column vector of an signal observed
in the ith channel. The concatenated signal y is con-
CONCATENATION METHOD FOR HIGH-TEMPORAL RESOLUTION SSVEP-BCI
445
5 10 15 20 25 30 35 40
0
100
200
Fourier power of Oz signal
Frequency (Hz)
5 10 15 20 25 30 35 40
0
100
200
Mean Fourier power of O1, Oz, and O2 signal
Frequency (Hz)
5 10 15 20 25 30 35 40
0
200
400
Fourier power of Concatenated signal
Frequency (Hz)
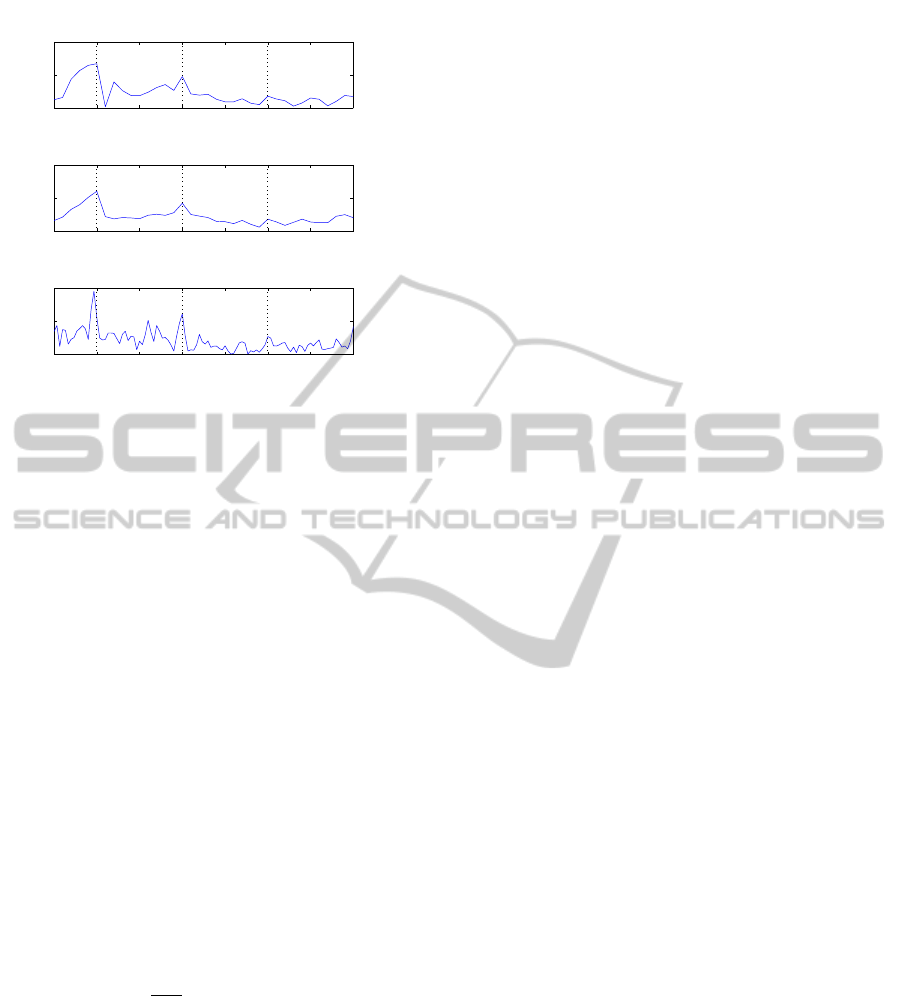
Figure 2: Frequency features of concatenated signal: Top,
Fourier power |X
Oz
(e
jω
)|
2
; Middle, mean Fourier power of
|X
cha
(e
jω
)|
2
(cha = [O1, Oz,O2]); Bottom, Fourier power
|Y(e
jω
)|
2
from a concatenated signal of O1, Oz, and O2.
structed by concatenating signals in the time domain:
y = [x
1
T
,x
2
T
,...,x
M
T
]
T
, (1)
where M is the number of concatenated signals and T
represents transposition. If each signal is of length N,
then y is of length MN. Furthermore, let X
i
(e
jω
) (resp
Y(e
jω
)) be the Fourier transform of x
i
(resp. y). Fre-
quency resolution of Y(e
jω
) is M times higher than
that of X
i
(e
jω
). It can be explained by the larger size
of y. Using ω = 2π f (f is frequency), short time
Fourier transforms of these signals are expressed as
X
i
(e
jω
) = X
i
(e
2π j f
) =
N−1
∑
t=0
x
i
[t]e
−2π j ft
(2)
and
Y(e
jω
) = Y(e
2π j f
) =
MN−1
∑
t=0
y[t]e
−2π j ft
, (3)
where
f =
kL
MN
[Hz] (k∈N), (4)
and t and L represent time index and the time length
of 1 s, respectively. k represents the number of cy-
cles of a sinusoidal signal within the time window of
the Fourier transform. e
jω
should be 0 at the begin-
ning and the end of the epoch. Frequency resolutions
therefore are divided by the number of concatenations
M.
As an example, EEG electrodes are attached at Oz,
O1, O2, Pz, P1, and P2 according to the international
10/20 system. SSVEP of all signals are measured
while 10 Hz visual stimulus is displayed. x
Oz
, x
O1
,
and x
O2
correspond raw signals at Oz, O1, and O2,
for instance. Concatenated signal y can be defined
like [x
Oz
T
,x
O1
T
,x
O2
T
]. Here, we consider signals
x
Oz
, and y ([x
Oz
T
,x
O1
T
,x
O2
T
). Time length of each
EEG signal x
i
is 1 s (1 s epoch). In the Fig. 2, Fourier
power |X
Oz
(e
jω
)|
2
has weak peaks around 10 and 20
Hz. The mean of |X
cha
(e
jω
)|
2
(cha = [O1,Oz,O2])
has similar peak of |X
Oz
(e
jω
)|
2
. Contrary to that,
Fourier power of concatenated signal |Y(e
jω
)|
2
has
stronger peak near 10 and 20 Hz.
Furthermore, we investigate effects of the num-
ber of signals: x
Oz
, y
1
([x
Oz
T
,x
O1
T
]
T
), y
2
([x
Oz
T
,x
O1
T
,x
O2
T
,x
Pz
T
,x
P1
T
,x
P2
T
]
T
). With these
signals, Fig. 3 shows Fourier power |X
Oz
(e
jω
)|
2
,
|Y
1
(e
jω
)|
2
, |Y
2
(e
jω
)|
2
in two different conditions: x
i
is 1 s or 2 s length. The Hanning window is of
length MN. From the figure, regardless of 1 s epoch
and 2 s epoch, the peak at 10 Hz appears more and
more clearly as the number of concatenated signals
increases. Thus, the concatenation method can ex-
tract sharper peak of SSVEP despite of short time
epoch. Furthermore, different window functions can
be used: no window function, Hanning window of
same length as the concatenated signal, or Hanning
window of same length as each signal, respectively.
In Fig. 3, Hanning window of same length as the con-
catenated signal is applied and it is also used in the
next sub-section.
Finally, concatenation of a EEG signals repetively
were investigated. It uses only one EEG signal.
This concatenated signal is expressed as y
same
=
[x
T
,x
T
,...,x
T
]
T
. Fourier powers of this signal with
different time epochs are shown in Fig. 4. These are
small peaks at 1 Hz interval in Fig. 4-(a), 0.5 Hz inter-
vals in Fig. 4-(b), and 0.2 Hz intervals in Fig. 4-(c). It
may be a problem for detection of SSVEP peaks. It is
obviously explained by the property of Fourier trans-
form (see APPENDIX). Therefore, concatenation of
EEG signals from different channels conduces better
observation of SSVEP peaks.
3 EXPERIMENTAL
DEMONSTRATION
Eight subjects took part in the experiment, and signed
written informed consent forms. EEG signals were
taken from a database recorded during SSVEP stimu-
lation in Riken BSI/Japan. Photic stimulation is given
using AVOTEC goggles and the flickering frequency
is controlled by a shutter which allows a maximal re-
freshing rate of 293 Hz. A very broad range of fre-
quencies is recorded (21 different frequencies from
1 Hz to 100 Hz): 1.00, 1.25, 1.88, 2.50, 3.33, 4.17,
NCTA 2011 - International Conference on Neural Computation Theory and Applications
446

5 6 7 8 9 10 11 12 13 14 15
0
200
Frequency (Hz)
Power
5 6 7 8 9 10 11 12 13 14 15
0
500
Frequency (Hz)
Power
(a1)1sepoch,onesignal (b1)2sepoch,onesignal
5 6 7 8 9 10 11 12 13 14 15
0
500
Frequency (Hz)
Power
5 6 7 8 9 10 11 12 13 14 15
0
500
Frequency (Hz)
Power
(a2)1sepoch,twosignals (b2)2sepoch,twosignals
5 6 7 8 9 10 11 12 13 14 15
0
1000
Frequency (Hz)
Power
5 6 7 8 9 10 11 12 13 14 15
0
1000
2000
Frequency (Hz)
Power
(a3)1sepoch,sixsignals (b3)2sepoch,sixsignals
Figure 3: Frequency features of concatenated signal: Left three figures, length of each EEG signal is 1 s (1 s epoch); Right
three figures, length of each EEG signal is 2 s (2 s epoch); Top two figures, Fourier power |X
Oz
(e
jω
)|
2
; Middle two figures,
Fourier power |Y
1
(e
jω
)|
2
(y
1
is of Oz and O1); Bottom three figures, Fourier power |Y
2
(e
jω
)|
2
(y
2
is of Oz, O1, O2, Pz, P1,
and P2).
5 6 7 8 9 10 11 12 13 14 15
0
500
1000
Frequency (Hz)
Power
(a) y
same
,1sepoch,eightsignal
5 6 7 8 9 10 11 12 13 14 15
0
1000
Frequency (Hz)
Power
(b) y
same
,2sepoch,eightsignals
5 6 7 8 9 10 11 12 13 14 15
0
1000
2000
Frequency (Hz)
Power
(c) y
same
,5sepoch,eightsignals
Figure 4: Frequency features of y
same
with eight same sig-
nals: Top, 1 s epoch; Middle, 2 s epoch; Bottom, 5 s epoch.
5.00, 6.67, 8.33, 10.00, 13.33, 16.67, 20.00, 26.67,
33.33, 40.00, 53.33, 66.67, 80.00, 90.00, and 100.00
Hz. Firstly a subject sees a uniform grey screen for
20 s, then a flickering stimulus for 10 s, and then iter-
atively restarts this sequences of rest/stimulus condi-
tion. Stimuli were presented in a randomized order, in
seven runs of nine frequencies, for a total of 63 trials
(3 trials per 21 frequency).
EEG was recorded using a Biosemi system in a
shielded room, with 128 active channels, all signals
were amplified and digitized at 1024 Hz, after ana-
log filtering of frequencies above 100 Hz and notch
filtering at 50 Hz.
In this paper, parts of EEG channels are used as
Figure 5: A placement of electrodes which are used for
analysis in this paper.
shown in Fig. 5 (12 EEG channels: Fp1, Fpz, Fp2,
F1, Fz, F2, P1, Pz, P2, O1, Oz, and O2) and visual
stimuli of 10 and 13.33 Hz are used to investigate ef-
fectiveness of the concatenation method.
4 RESULTS
In this section, SSVEPs evoked by 10 and 13.33 Hz
stimuli are investigated. First of all, EEG features to
classify the SSVEPs are detailed. Then, SSVEPs of
10 and 13.33 Hz are classified with several features
selected by a supervised feature ranking method, the
Gram-Schmidt orthogonalization. Finally, we com-
pare the frequency domain of a concatenated signal
with that of the signals which are used for concatena-
tion.
CONCATENATION METHOD FOR HIGH-TEMPORAL RESOLUTION SSVEP-BCI
447

4.1 EEG Feature Extraction
SSVEP responses have peaks at the stimulus fre-
quency and even harmonics (Fig. 1). Using 10 and
13.33 Hz as stimulus frequencies, SSVEPs are de-
scribed by six different features for the purpose of
classification: ξ
1
, the spectral power at the stimu-
lation frequency; ξ
2
, the frequency power enhanced
by SSVEP SNR (Vialatte et al., 2010) applied to the
frequency domain; ξ
3
, the magnitude square coher-
ence function between two signals; ξ
4
, global field
synchronization; ξ
5
and ξ
6
, the frequency power and
SSVEP SNR of the concatenated signals.
The first feature is defined as
ξ
1
( f ) = |X( f)|
2
+ |X( f×2)|
2
, (5)
i.e. sum of the spectral powers of the fundamental
and its first harmonic. This feature is extracted at
each channel of both 10 and 13.33Hz. Although ξ
2
has similar feature with ξ
1
, SSVEP peaks can be en-
hanced by SSVEP SNR as
X
′
( f ) =
nX( f)
∑
n/2
k=s
X( f + k△ f) +
∑
n/2
k=s
X( f − k△ f)
, (6)
and then the second feature can be defined as
ξ
2
( f ) = |X
′
( f )|
2
+ |X
′
( f ×2)|
2
. (7)
The coherence function, a synchrony measure, is
distinguished into the magnitude square coherence
function and the phase coherence function (see for in-
stance (Nunez et al., 1997; Dauwels et al., 2010)).
Magnitude square coherence function is the third fea-
ture we used. It is defined as
ξ
3
i, j
( f ) =
|X
i
( f )X
∗
j
( f )|
2
|X
i
( f )||X
j
( f )|
, (8)
where X
∗
is the complex conjugate of X, i and j cor-
respond to the label of channel. It is a function of two
signals, therefore, the number of pairs of all channels
corresponds to the number of combinations.
Similarly, global field synchronization (GFS),
another synchrony measure, is the fourth fea-
ture. GFS quantifies the synchrony of multi-
ple signals. First of all, with Fourier trans-
formed signals, one constructs the vectors X
R
( f ) =
(Re(X
1
( f )),Re(X
2
( f )),...,Re(X
M
( f )))
T
and X
l
( f ) =
(Im(X
1
( f )),Im(X
2
( f )),...,Im(X
M
( f )))
T
, and com-
putes the covariance matrix C∈R
2×2
for those two
vectors. GFS (ξ
4
( f )) is defined in terms of the nor-
malized eigenvalues λ
1
and λ
2
of C:
ξ
4
( f ) = λ
1
− λ
2
. (9)
Finally, with concatenated signals, the Fourier
power and SSVEP SNR are defined as
ξ
5
( f ) = |Y( f )|
2
+ |Y( f×2)|
2
, (10)
ξ
6
( f ) = |Y
′
( f )|
2
+ |Y
′
( f ×2)|
2
. (11)
Here, we used six groups of channels for concatena-
tion: (Fp1-Fpz-Fp2), (F1-Fz-F2), (P1-Pz-P2), (O1-
Oz-O2), (Fp1-Fpz-Fp2-F1-Fz-F2), and (P1-Pz-P2-
O1-Oz-O2).
There are six different features with different pa-
rameters. There are parameters of two stimulus fre-
quencies and the channel locations for all features;
and the window functions, and channel groups which
are only for concatenated feature. We prepared two
different conditions:
1. Condition 1 includes the Fourier, SSVEP SNR,
coherence and GFS feature. In this condition,
the total number of feature is 24(ξ
1
) + 24(ξ
2
) +
132(ξ
3
) + 2(ξ
4
) = 182.
2. Condition 2 includes the Fourier and SSVEP SNR
of each EEG signal, that of the concatenated sig-
nals, coherence and GFS feature. In this con-
dition, the total number of features is 24(ξ
1
) +
24(ξ
2
) + 132(ξ
3
) + 2(ξ
4
) + 24(ξ
5
) + 24(ξ
6
) =
230.
4.2 SSVEP Classification
For classifying the SSVEPs, the number of features
must be as small as possible (see for instance (Drey-
fus, 2005)). Input ranking thorough Gram-Schmidt
orthogonalization is applied to select all relevant fac-
tors as inputs to the classifier, but only the relevant
ones. The relevance is measured by the angle between
the vector of a feature (ξ
i
) and the vector of stimuli la-
bel (l) as
cos
2
θ
i
=
|(ξ
i
)
T
l|
2
|(ξ
i
)
T
ξ||l
T
l|
. (12)
Firstly, a feature which is most correlated to the fea-
ture (l) is chosen by the largest cos
2
θ
i
. l and all other
candidate inputs are projected onto the null space of
the selected input (subspace). The above procedure
is iterated until all features have been ranked. With
ranked features, SSVEPs are classified by linear dis-
criminant analysis (LDA). Performances are defined
as the classification accuracy (ACC) calculated with
leave one out cross validation (LOOCV). These pro-
cedures are applied for two cases (two frequencies):
using all features except concatenation features (Con-
dition 1) and using all features (Condition 2). Addi-
tionally, we use four different time epochs (1.0, 2.0,
5.0, 10.0 s).
Table 1 shows ranked top 10 features thorough
Gram-Schmidt orthogonalization. These results are
performed with 1 s epoch. Mostly, ξ
1
, ξ
2
, ξ
3
with
different parameters are chosen when concatenation
NCTA 2011 - International Conference on Neural Computation Theory and Applications
448

Table 1: Feature ranking with 1 s epochs: FT represents ξ
1
, SNR represents ξ
2
, MC represents ξ
3
, ConcateFT represents
ξ
5
, and ConcateSNR represents ξ
6
. The ranking is calculated firstly without the concatenation features (Condition 1), then
including them (Condition 2). Concatenation features were chosen in high ranks.
Rank Condition 1 Condition 2
(without councatenation) (with councatenation)
1 FT (P22, 13.33 Hz) ConcateFT (group6, 10 Hz, window2)
2 FT (F2, 10 Hz) ConcateFT (group2, 13.33 Hz, window1)
3 SNR (Oz, 13.33 Hz) ConcateSNR (group6, 10 Hz, window1)
4 SNR (O2, 10 Hz) SNR (O2, 10 Hz)
5 MC (F1-P2, 10 Hz) ConcateSNR (group3, 13.33 Hz, window3)
6 MC (F1-P2, 13.33 Hz) ConcateSNR (group2-1, 13.33 Hz, window3)
7 MC (Fpz-P1, 10 Hz) MC (F1-P2, 10 Hz)
8 MC (Fpz-F2, 13.33 Hz) MC (Fpz-P1, 10 Hz)
9 MC (Fp2-Oz, 13.33 Hz) MC (F1-O1, 10 Hz)
10 SNR (Fz, 13.33 Hz) MC (Fp1-O2, 10 Hz)
0 50 100
0.6
0.7
0.8
0.9
1
Number of features
ACC
Condition 1
1.0 s
2.0 s
5.0 s
10.0 s
0 50 100
0.6
0.7
0.8
0.9
1
Number of features
ACC
Condition 2
1.0 s
2.0 s
5.0 s
10.0 s
Figure 6: ACC result estimated by LDA. Left figure is in the condition without concatenation features. Right figure is in
the condition with concatenation features. ACCs with 1 and 2 epoch look higher in Condition 2. ACC with 5 s is stable in
Condition 2 although it seems to be over fitting to the training data in Condition 1 due to such as having too many features.
Table 2: ACC comparison between Condition 1 and Condition 2. Maximum ACC of all nu ((1≤nu≤100)) is higher in
Condition 2 in all time epochs. Furthermore, with 1 s epoch, ACC in Condition 2 is higher in all numbers of features and it
shows +0.06 when nu = 40.
Features conditions Number of features Maximum of all Minimum of all
nu=1 nu=10 nu=20 nu=40 nu=100 nu (1≤ nu≤100) nu (1≤nu≤100)
t=1 Condition 1 0.68 0.78 0.80 0.79 0.77 0.82 0.68
Condition 2 0.70 0.80 0.81 0.85 0.82 0.86 0.70
t=2 Condition 1 0.76 0.83 0.88 0.90 0.86 0.91 0.76
Condition 2 0.76 0.86 0.87 0.86 0.94 0.94 0.76
t=5 Condition 1 0.84 0.92 0.94 0.95 – 0.97 0.59
Condition 2 0.84 0.94 0.96 0.97 – 1.00 0.84
t=10 Condition 1 0.81 0.98 1.00 – – 1.00 0.81
Condition 2 0.81 0.98 1.00 – – 1.00 0.81
features are not included. On the contrary, concate-
nation feature ξ
5
and ξ
6
are ranked top 6 only except
rank 5 is ξ
2
when concatenating features are included.
Furthermore, ACCs depending on number of features
are shown in Fig. 6. Table 2 shows ACC shown in
Fig. 6 when numbers of features are 1, 10, 20, 40,
and 100. From the figure, ACCs with 1 and 2 epoch
looks higher in Condition 2. Moreover, ACC with 5 s
is stable in Condition 2 although it seems to be over
fitting to the training data in Condition 1 due to such
as having too many features. From the table, firstly,
maximum ACC of all nu (1≤nu≤100) is higher in
CONCATENATION METHOD FOR HIGH-TEMPORAL RESOLUTION SSVEP-BCI
449

t=1.0 t=2.0 t=5.0 t=10.0
0
0.1
0.2
0.3
0.4
0.5
Window size (s)
Error rate
Error rates using Fp1, Fp2, and Fpz
Mean of Fourier powers
Fourier power with concatenation
t=1.0 t=2.0 t=5.0 t=10.0
0
0.1
0.2
0.3
0.4
0.5
Window size (s)
Error rate
Error rates using P1, P2, and Pz
Mean of Fourier powers
Fourier power with concatenation
t=1.0 t=2.0 t=5.0 t=10.0
0
0.1
0.2
0.3
0.4
0.5
Window size (s)
Error rate
Error rates using F1, F2, and Fz
Mean of Fourier powers
Fourier power with concatenation
t=1.0 t=2.0 t=5.0 t=10.0
0
0.1
0.2
0.3
0.4
0.5
Window size (s)
Error rate
Error rates using O1, O2, and Oz
Mean of Fourier powers
Fourier power with concatenation
t=1.0 t=2.0 t=5.0 t=10.0
0
0.1
0.2
0.3
0.4
0.5
Window size (s)
Error rate
Error rates using Fp1, Fp2, and Fpz
Mean of Fourier powers
Fourier power with concatenation
t=1.0 t=2.0 t=5.0 t=10.0
0
0.1
0.2
0.3
0.4
0.5
Window size (s)
Error rate
Error rates using P1, P2, Pz, O1, O2, and Oz
Mean of Fourier powers
Fourier power with concatenation
Figure 7: Training error rate comparing concatenation features and average of Fourier powers. In each figure, different EEG
channels are used. Compared with these features, concatenation features has lower error rate than average of Fourier powers,
especially in parietal and occipital areas.
Condition 2 in all time epochs. Secondly, with 1 s
epoch, ACC in Condition 2 is higher in all numbers
of features and it shows +0.06 when nu = 40.
4.3 Concatenation Method Vs.
Averaging of Signals
Finally, we compare the frequency power of a con-
catenated signal with that of the signals which are
used in concatenation. The average of Fourier pow-
ers of these signals is defined as
ξ
7
( f ) =
1
NumChannel
NumChannel
∑
channel
(ξ
1
( f,channel),
(13)
where channel and NumChannel represents each
channel and total number of channels of each group,
respectively. This feature is compared with the con-
NCTA 2011 - International Conference on Neural Computation Theory and Applications
450

catenation feature ξ
5
to prove the effectiveness of the
concatenation method.
For comparison, SSVEP is classified with LDA
classification with only ξ
5
or only ξ
7
. There are two
kinds of stimulus frequencies as parameters (10 and
13.33 Hz). Fig. 7 shows learning error rate in those
cases. One can observe on this figure that error rates
with concatenation features are systematically lower
than those with averaged Fourier powers.
5 DISCUSSIONS
With the concatenation method, we can obtain not
only higher frequency resolution but also higher peak
of Fourier power at the stimulus frequency. There-
fore, it may work effectively in the situation where
high temporal resolution of SSVEP detection is re-
quired. This method only requires signals concatena-
tion, consequently, it is not computationally demand-
ing, and can be used in real time processing. It re-
duces the patients’ stress when using SSVEP-BCI.
The patients are not required to focus for more than
one second, as evidenced by the 0.86 classification
accuracy with 1 s epoch (Table 2).
In our future works, we intend to confirm effects
of concatenating points with artificial signals, and in
addition to EEG signals. Moreover, using a larger
number of EEG channels could allow us to go down
to even shorter EEG epochs. One of the unsolved
problems is that each EEG epoch has different phase
and amplitudes at their borders. Therefore, the cy-
cles in each epoch do not match perfectly, which most
probably reduces the SSVEP peaks in the Fourier
spectrum. Improved algorithms for windowing EEG
epochs, and for matching their phase differences, are
to be developed.
6 CONCLUSIONS
A concatenation method is proposed to improve the
frequency resolution of Fourier spectrum when using
short EEG epochs. It successfully detected SSVEP
response by concatenating EEG epochs in the time
domain, down to 1 s windows. Classification tests on
EEG data proved that concatenation method works
better than the averaging of Fourier spectrums com-
puted from the EEG epochs.
REFERENCES
Bashashati, A., Fatourechi, M., and Ward, R. K. (2007).
A survey of signal processing algorithms in brain-
computer interfaces based on electrical brain signals.
J. Neural Engineering, 4:R32–R57.
Bin, G., Gao, X., Yan, Z., Hong, B., and Gao, S. (2009). An
online multi-channel ssvep-based brain-computer in-
terface using a canonical correlation analysis method.
J. Neural Engineering, 6(4):046002.
Birbaumer, N. (2006). Breaking the silence: brain-
computer interfaces (bci) for communication and mo-
tor control. Psychophysiology, 43:517–532.
Dauwels, J., Vialatte, F.-B., Musha, T., and Cichocki, A.
(2010). A comparative study of synchrony measures
for the early diagnosis of alzheimer’s disease based on
eeg. NeuroImage, 49:668–693.
Dreyfus, G. (2005). Neural networks: methodology and
applications. Springer-Verlag.
Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih,
H. H., Zheng, Q., Yen, N.-C., Tung, C. C., and Liu,
H. H. (1998). The empirical mode decomposition and
hilbert spectrum from nonlinear and non-stationary
time series analysis. In R. Soc. Lond. A, volume 454,
pages 903–995.
Kawabata, N. (1973). A non-stationary analysis of the elec-
troencephalogram. IEEE Trans Biomed Eng, 20:444–
452.
Lotte, F., Cogedo, M., Lecuyer, A., Lamarche, F., and Ar-
naldi, B. (2007). A review of classification algorithms
for eeg-based brain-computer interfaces. J. Neural
Engineering, 4:R1–R13.
Nunez, P. L., Srinivasan, R., Westdorp, A. F., Wijesinghe,
R. S., Tucker, D. M., Silberstein, R. B., and Cadusch,
P. J. (1997). Eeg coherency: l: statistics, refer-
ence electrode, volume conduction, laplacians, cor-
tical imaging, and interpretation at multiple scales.
Electroencephalography and Clinical Neurophysiol-
ogy, 103:499–515.
Quiroga, R., Sakowitz, O., Bas¸ar, E., and Sch¨urmann, M.
(2001). Wavelet transform in the analysis of the fre-
quency composition of evoked potentials. Brain Re-
search Protocols, 8:16–24.
Sanei, S. and Chambers, J. A. (2007). EEG signal process-
ing. Wiley, Lodon.
Vialatte, F., Sol´e-Casals, J., and Cichocki, A. (2008). Eeg
windowed statistical wavelet scoring for evaluation
and discrimination of muscular artifacts. Physiolog-
ical Measurements, 29(12):1435–1452.
Vialatte, F.-B., Maurice, M., Dauwels, J., and Cichocki, A.
(2010). Steady-state visually evoked potentials: fo-
cus on essential paradigms and future perspectives.
Progress in Neurobiology, 90:418–438.
CONCATENATION METHOD FOR HIGH-TEMPORAL RESOLUTION SSVEP-BCI
451

APPENDIX
Since y is defined as (1), Fourier transform of y is
expressed as
Y(e
jω
) =
MN−1
∑
t=0
y[t]e
− jωt
=
N−1
∑
t=0
x
1
[t]e
− jωt
+
2N−1
∑
t=N
x
2
[t − N]e
− jωt
+... +
MN−1
∑
t=(M−1)N
x
M
[t − (M− 1)N]e
− jωt
=
M
∑
i=1
iN−1
∑
t=(i−1)N
x
i
[t − (i− 1)N]e
− jωt
. (14)
It also can be expressed as
Y(e
2π j f
) =
M
∑
i=1
iN−1
∑
t=(i−1)N
x
i
[t − (i− 1)N]e
−2π j ft
, (15)
using ω = 2π f. Furthermore, if the same signals are
concatenated (in the case of y
same
),
x
1
= x
2
= ... = x
M
= x, (16)
then, (15) becomes
Y(e
2π j f
) =
M
∑
i=1
iN−1
∑
t=(i−1)N
x[t − (i− 1)N]e
−2π j ft
. (17)
Under this condition, the constant interval depending
on the time epoch is in the case of
k = mM (m∈N), (18)
then, (19) becomes
f =
kL
MN
=
mML
MN
=
mL
N
. (19)
In the case of this condition,
e
−2π j ft
= e
−2π j f(t+nN)
(n = ... − 2,−1,0, 1,2,...)
(20)
then, (17) becomes
Y(e
2π j f
) = M
N−1
∑
t=0
x[t]e
−2π j ft
. (21)
Therefore, if (16) and (18), Fourier spectrum is M
times higher than that of an EEG signal and it has
same power distribution with each signal. Consider-
ing time epochs of 1 s, 2 s, and 5 s in Fig. 4, the
emphasized frequencies are expressed as
f =
m if L = N (1s epoch)
m/2 i f L = 2N (2sepoch)
m/5 i f L = 5N (5sepoch)
(22)
using (19).
NCTA 2011 - International Conference on Neural Computation Theory and Applications
452
