APPLICATION OF MATHEMATICAL TRANSFORM

IN DETECTION ALGORITHMS

Lyubka A. Doukovska

Institute of Information and Communication Technologies, Bulgarian Academy of Sciences

Acad. G. Bonchev str., bl. 2, 1113, Sofia, Bulgaria

doukovska@iit.bas.bg

Keywords: Hough transform, Radar detector, Target detection, Parameter estimation, Probability of detection, Constant

false alarm rate.

Abstract: Recent trends in the design of highly efficient and fully automated systems for processing radar data in

terms of a priori uncertainty about the targets and disturbances are causing the researchers to use the latest

achievements in the design of real time computing architectures for optimum realization and high

performance. The development of new algorithms that can be used to retrieve information about targets,

applying a mathematical transformation on the received signals yielding estimates of the parameters of

moving targets with extremely high precision in a dynamically changing radar environment is a new and

very promising direction in modern information and communication technologies. This article discusses

such an approach applying the Hough transform to determine the coordinates of the targets. The approach

uses a finite set of preselected patterns of the target movement. The Hough transform, translates the set of

measurements received in the space of patterns. Association to one or another specific pattern is done

estimating the information about the coordinates extracted from the received signals. Thus the moving target

parameters in the surveillance zone are uniquely determined by the parameters of the pattern.

1 INTRODUCTION

In the recent years development of modern highly

effective algorithms with optimal statistic

characteristics for real time radiolocation data

processing is becoming a very actual scientific task.

Nowadays algorithms that extract information about

target’s behavior through mathematical

transformation of the signals reflected from a target,

find ever-widening practical application. Applying

signal transformation allows for higher accuracy of

the estimated moving target parameters in dynamic

radiolocation environment. That is why development

of new robust and reliable algorithms for

simultaneous trajectory and target detection applying

the Hough transform is a perspective field of

research, so the present paper considers this

problem. The performance of original Hough

detector structures maintaining constant false

trajectory detection probability in intensive

randomly arriving impulse interference environment

is studied. Estimated are the efficiency and quality

of the obtained algorithms for data streams with

different distribution lows of occurrence of impulse

interference. A comparative analysis of the

presented Hough detector structures is made. The

practical effect of the obtained results lies in the

possibility of development of radar signal processing

algorithms for automated systems of air traffic

control service.

On 18.Dec.1962 the American Patent Service

issued a patent 3,069,654 “Method and means for

recognizing complex patterns” on the name of Paul

V. C. Hough (Hough, 1962). The Hough transform

is a mathematical conversion, in which the task for

finding specific features of the processed image

consisting of points defined in the feature space is

transformed to a task for finding groups of points in

the parameter space. The Hough transform for

straight lines detection is a sub case of the Radon

transform which for the Euclidean two dimensional

space and arbitrary generalized function F(x, y) is as

follows:





















dxdyyxyxFFRf



sincos,,

(1)

where







is the Dirac delta function defining the

integral on direction of a straight line defined by the

161

Doukovska L.

APPLICATION OF MATHEMATICAL TRANSFORM IN DETECTION ALGORITHMS.

DOI: 10.5220/0004459801610167

In Proceedings of the First International Symposium on Business Modeling and Software Design (BMSD 2011), pages 161-167

ISBN: 978-989-8425-68-3

equation:





sincos yx 

Initially Hough transform proposed in (Hough,

1962) presents the straight lines from a two-

dimensional image in the features space (FS) with

incidence m and segment c from

cmxy 

, where

x and y are the image coordinates and m and c are

the coordinates in parameter space (PS).

The parameter space is sampled to a set of

subspaces (accumulators). Each point of the input

image is projected onto a straight line with

coordinates (m, c). Accumulators through which this

line passes increase their content by one. Each of

these accumulators corresponds to an area in the

features space and the presence of a peak in the

accumulator corresponds to a straight line or a

segment of the image. Lines existing in the features

space are detected according to the value

accumulated into an accumulator in the parameter

space. Hough transform proves to be a major tool in

the analysis and algorithms for pattern recognition.

The concept of using the Hough transform for

target detection improvement is introduced in

(Carlson, Evans and Wilson, 1994). Regardless of

the particular application of the Hough transform,

different authors point three of its main properties

that make it applicable to moving targets detection:

- Applicable for raster images;

- Applicable for fuzzy images processing;

- Effective when there is a lack of necessary

information (measurements, observations).

2 HOUGH TRANSFORM FOR

MOVING TARGET

DETECTION

Let us consider the operation of surveillance radar

which measures the distance, targets azimuth,

elevation and Doppler velocity as a function of time.

The sampling time is specified. Trajectory detection

by means of Hough transformation can be made

either having rotating antenna or phased array

(Carlson, Evans and Wilson, 1994). In a single

resolution cell in azimuth the traditional radars emit

several pulses on a specified carrier frequency. The

surveillance area is being consequently scanned with

the radar antenna pointing in different directions.

This procedure is repeated on successive periods of

time equal to the sampling time. In each “azimuth-

distance” resolution cell the station processes non-

coherent accumulation of the emitted pulses. The

target is considered detected if the pulse amplitude

in the (azimuth-distance) resolution cell exceeds a

preset threshold. This approach has some difficulties

to detect fast moving targets, because these objects

move quickly from one to another resolution cell

during one sampling period.

If received by the radar echo signals are arranged

as discrete multidimensional array, i.e. discrete

information card (with 5 dimensions - distance,

azimuth, elevation, Doppler velocity and time), the

target will appear as a curve, which intensity

depends on the power level of the echo signals. If

this curve can be monitored, it contains all the

accumulated information about the target and

complete history of its trajectory. Object with

constant radial velocity appears as a straight line.

The projection of this 5-dimensional information

about distance and time is a convenient way to

display the curve, while no interest in the other three

levels for this target. The result is a so-called “range

– time” (r-t) space.

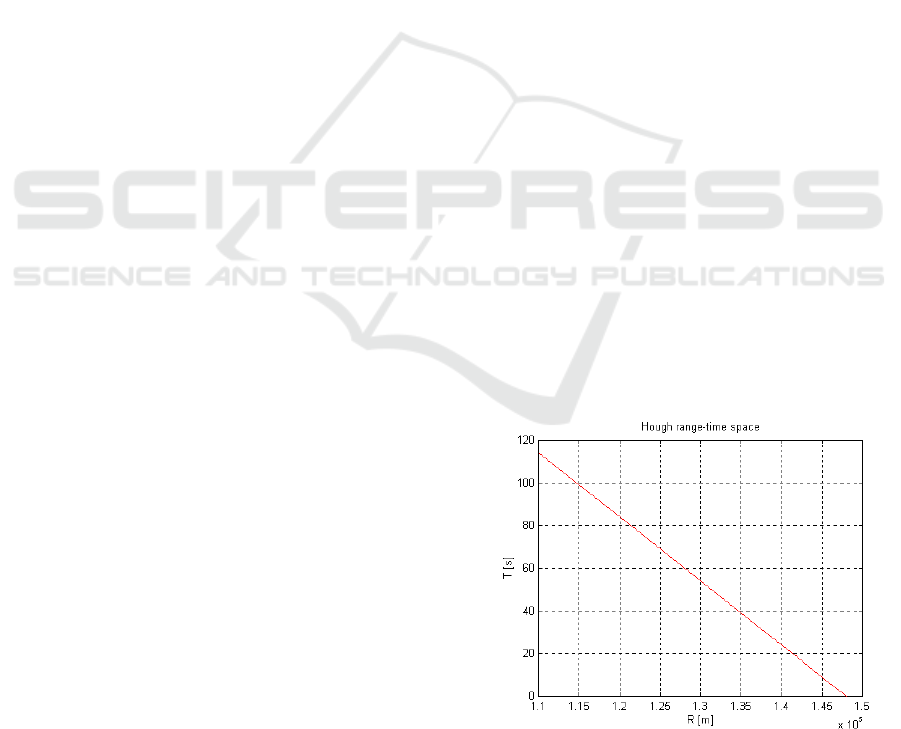
Figure 1 shows (r-t) space of a target with a

constant radial velocity, with given direction of the

antenna beam to a specified resolution cell of the

Doppler velocity. The slope of this line is

determined by the radial velocity of the target. The

trajectory of a stationary object will appear as a

vertical line. All moving objects will have a certain

angle, reaching zero for the fastest objects.

Time axis starts from zero to maximum. It is

convenient to present the information about the past

to a decent level, because too old information is not

useful. The current information contains the

disturbance, which is an internal white noise of the

receiver. It has Rayleigh amplitude distribution and

is summed in each cell of (r-t) space. The problem is

to find a straight line on the background of the noise.

Figure 1: “Range-time” space.

The Hough transform is a method detecting

curve elements, often used to detect location lines on

BMSD 2011 - First International Symposium on Business Modeling and Software Design

162

the noise background. Other forms of trajectories

can be also detected, but so far only straight lines

have been investigated.Figure 2 shows several data

points that form a straight line in the “range – time”

space. In polar coordinates, a straight line can be

accurately defined by two parameters:



- the angle between the perpendicular from the

coordinate system origin in (r-t) space to the straight

line and the abscissa axis;



- length of the perpendicular, i.e. the distance

between the coordinates origin in (r-t) space and the

line.

Figure 2: Relation between “range-time” (r-t) space and

Hough transform.

The Hough transform translates the points from

(r-t) information space to (-) or Hough parameter

space using the following expression:





sincos tr 

(2)

where r and t are coordinates in the (r-t) space.

The Q grid in Hough space is formed by

consequent change of



angle form 0 to 180 and

calculating the corresponding



. Sometimes another

form of the Hough transform is used:















arctgtr



sin

(3)

The transform results in a sinusoid with phase and

amplitude defined by the (r-t) value of the

information point. The maximal



value is equal to

the length of the diagonal in the (r-t) space. The

transformation according (2) is shown on Figure 3.

Each point in (-) space corresponds to a separate

straight line in (r-t) space defined by the values of



and



. Each sinusoid presents a set of possible

straight lines through the point. If there are points

forming a straight line in the (r-t) space this

corresponds to an intersection point of set of

sinusoids in the Hough space. The (r-t) space is

sampled to cells which number is equal to the

number of the distance resolution elements and the

sample numbers. The primary threshold is used for

signal detection in each (r-t) cell. When the signal

value in a specified (r-t) cell exceeds the primary

threshold, its power gets added to the (-) cell

being intersected by the corresponding sinusoid in

the Hough space. Thus the value of an accumulator

cell in the intersection of several sinusoids will

become higher.

Figure 3: Hough parameter space.

The secondary threshold applied to each cell in

the parameter space may declare straight line

trajectory detection. This is the accumulated for

several scans moving target echo signal. The



and



parameters of the tracked straight line trajectory in

Hough space might be transformed back to the (r-t)

space indicating the current object position.

Transition from (r-t) to parameter space is being

made by means of a simple matrix manipulation.

Matrix D contains I number of elements where the

signal value exceeding the primary threshold.















...

(4)

Transformation matrix H consists of sinusoids and

cosinusoids from (2) defined as:

















cos

...

cos

sin

...

sin

(5)

where



are discrete values of Q from 0 to 180,

obtained during the sizing of the parameter space.

APPLICATION OF MATHEMATICAL TRANSFORM IN DETECTION ALGORITHMS

163

The product of Н and D is a matrix R of size

I), which contains the corresponding



values.

The indices of the



elements in matrix R are the

indices of the points in (r-t) space where the primary

threshold has been exceeded.















NIN

HDR



,...,

111

(6)

Each column or the R matrix contains the



values

for one sinusoid on the parameter space. It is plain to

see the more points in (r-t) space exceed the primary

threshold the bigger D and R will be. The result is

increasing number of calculations. The size of

matrix H depends only on the parameter space

sampling.

The advantage of the Hough transform

application is the simultaneous target and its

trajectory detection. The target is considered

detected when its straight line trajectory is localized

in the Hough space, i.e.



and



parameters. When

applying the Hough transform additional non-

coherent integration of the signal obtained in several

consequent scans is done. This signal integration for

fast moving targets increases the detection

probability compared to the conventional radars. In

the recent years the Hough transform finds wide

application in moving targets detection (Carlson,

Evans and Wilson, 1994). This is a new and

perspective direction of the Hough transform

application and the results presented in (Kabakchiev,

Doukovska, Garvanov, 2005, Doukovska, 2007,

Doukovska 2007, Doukovska, 2008, Doukovska

2008, Doukovska, 2010) are dedicated to this

problem.

3 TARGET DETECTION SIGNAL

MODEL

The radar receives signal, noise and randomly

arriving impulse interference. In the present paper a

Swerling II target signal model is used. This model

is a package of echo signals with Rayleigh

distribution, reflected from a fast moving target. The

noise is a stationary and internal for the receiver.

The noise has normal distribution law which

corresponds to a Rayleigh distribution of the

envelope. Distribution function of the envelope of

the signal and the noise and the corresponding

density are





and





. If there is there is a

possibility for randomly arriving impulse

interference (RAII) -

е , (Poisson stream) the radar

resolution cells are filled with signal, noise and RAII

(Akimov, P., F. Evstratov, S. Zaharov, 1989). The

function and density distribution of the envelope in

this case are





and



The overall distribution function of the above

described case is obtained taking into account the

probability of absence of RAII is



1 e

and for

presence of RAII - (e

) respectively. Now the

distribution function of the envelope is (Akimov, P.,

F. Evstratov, S. Zaharov, 1989):













xFexFexF

sssP 2010

1 





(7)

The distribution density function is:













xfexfexf

sssP 2010

1 





(8)

Here it is assumed that the probability of RAII

appearing in a resolution cell is an infinitely small

quantity compared to the probability of single

impulse occurrence. This is a typical feature for a

Poisson stream.

When the duration of the impulse disturbance is

not negligible compared to the average period of

recurrence (high probability for RAII), a binomial

model of the stream distribution is used. In this case

the distribution function of the envelope

is (Akimov,

P., F. Evstratov, S. Zaharov, 1989):















 

xFexFeexFexF

ssssB 3

121 

(9)

For the distribution density of the envelope we have:

























xfexfeexfexf

ssssB 3

121 

(10)

where





and





- are function and

distribution density of the signal, the noise and two

pulse interferences.

In the presented paper it is assumed that the

distribution of the signal plus noise and the mixture

of signal, noise and RAII after the quadratic detector

have an exponential density (Akimov, P., F.

Evstratov, S. Zaharov, 1989):























exp



(11)

























exp



(12)

where s is the average value of the signal to noise

ratio. In this case the probability density function for

BMSD 2011 - First International Symposium on Business Modeling and Software Design

164

Poisson distribution model of the RAII has the

following expression (Bird J., 1982) – see (8):















































exp



(13)

For high probability of RAII, when the model is

binomial the noise density distribution function is

used as well as two pulse interferences:

























exp



(14)

In this case the probability density function for

binomial distribution of the RAII – see (10) is:







 





































































exp



(15)

a) Poisson RAII model

b) Binomial RAII model

Figure 4: Radar resolution cell filled with signal (s=70dB),

noise (

=1) and impulse interference (INR=30dB,

=0.1).

Figure 4 shows the two streams – a) Poisson and

b) Binomial. The cells that do not contain useful

signal are filled with receiver internal noise and

impulse interference. The cells containing signal are

filled according (13) and (15). The results are

obtained for: average receiver noise level 

=1,

signal to noise ratio - s=70dB, impulse interference

to noise ratio - INR=30dB and probability for RAII

0.1 for both distributions.

4 EXPERIMENTAL RESULTS

Recently a lot of robust moving target detection

algorithms for processing signals from noisy

environments are developed. As a result a bank of

Hough detectors making use of one and two

dimensional signal processors was created

(Kabakchiev, Doukovska, Garvanov, 2005,

Doukovska, 2007, Doukovska 2007, Doukovska,

2008, Doukovska 2008, Doukovska, 2010). All

these structures have been analytically studied and

by means statistical analysis has been compared to

each other as well as to results obtained by other

authors (Carlson B., E. Evans, S. Wilson, 1994). On

Figure 5 is presented the overall structure scheme of

an adaptive to the environmental conditions detector.

It consists of two main modules – signal processor

and Hough detector. Maintaining constant false

alarm rates at the detector’s output depends on the

chosen scalar factor (T



) of the CFAR signal

processor. The system input signal reflected from

the target is filtered with a simple sinusoidal signal

(complex signal compression), then it enters the

quadratic detector where the signal matrix of the

receiver is generated. This signal matrix is fed to the

CFAR processor. As a result at the output a binary

signal matrix is generated containing zeros and ones

presenting absence or presence of a signal in a given

radar resolution cell. The binary matrix is visualized

on the plot extractor. Results are stored in the so

called target coordinates record determined by the i-

th radar observation. For several consecutive scans

an interscan gathering of the plots of the target is

done. Then the (r-t) space is formed and using the

already processed data the trajectory is being

determined. The Hough transform is applied over

the points from the (r-t) space in order to transfer

them to the Hough space. As a result there is a

bunch of sinusoids which intersection point

accumulates the energy reflected from the target.

Comparing the value accumulated in this point (sum

of zeros and ones) to a preliminary chosen threshold

is the way to detect a target if the radar range resolu-

APPLICATION OF MATHEMATICAL TRANSFORM IN DETECTION ALGORITHMS

165

Figure 5: Generalized Hough detector structure.

tion cell. It the result is positive a reverse Hough

transform is applied in order to determine the

distance to the target for a given azimuth.

Presented paper considers the results obtained

from the analysis of different Hough detectors with

one and two dimensional signal processors

maintaining constant false alarm rates. To make the

results applicable they were compared in equal

conditions using equal criteria. The efficiency of the

Hough transform application was estimated by the

profit, gained during the detection process,

expressed by the signal to noise ratio as per the

criterion presented in (Rohling H., 1983).

Choosing the appropriate threshold constants

assures good detection results even for low values of

the SNR (Doukovska, 2010). Table 1 presents the

obtained threshold constants in equal experimental

conditions for the different detection structures and

different values of the binary rule in the Hough

parameter space.

Table 1: Threshold constants for different Hough

detectors.

Hough detectors T

=2/20 T

/20

CA Hough CFAR 672 1.186

EXC Hough CFAR 21880 3.225

Hough CFAR BI 0.000494 0.0000858

EXC Hough CFAR BI 1.1285 0.3161

API Hough CFAR 7.5 1.535

For comparison are shown the achieved results

for the detection probability of different Hough

detector structures, calculated for non optimal and

optimal values of binary rule in Hough parameter

space - T

= T

Mopt

/20, for following environment

parameter values - average power of the receiver

noise λ

=1, average interference-to-noise ratio (INR)

=30dB, probability for the appearance of impulse

interference with average length e

=0.1, N=16, L=16

and for probability of false alarm P

=10

-4

The results presented in this paper are obtained

after statistical analysis of the Hough detectors

detection probability in intensive noise environment

with very high probability for randomly arriving

impulse interference. Different Hough detector

structures with one and two dimensional CFAR

signal processors are studied.

All analytical conclusions necessary to convey

the experiments are considered in details in

(Kabakchiev, Doukovska, Garvanov, 2005,

Doukovska, 2007, Doukovska 2007, Doukovska,

2008, Doukovska 2008, Doukovska, 2010).

Figure 6: Probability characteristics of a Hough detector

with one dimensional signal processors - cell averaging

CFAR (CA CFAR), excision CFAR processor (EXC

CFAR) and with fixed threshold, for RAII probability - e

It was shown that application of a binary CFAR

processor significantly increases the detection

quality (about 30dB) compared to the fixed

BMSD 2011 - First International Symposium on Business Modeling and Software Design

166

threshold algorithm (Doukovska, 2007). Analyzed is

a Hough detector with a more efficient structure of

the two dimensional CFAR processor with excision

censoring procedure in the reference window (EXC

CFAR BI). The hypothesis that censoring techniques

increase the detection efficiency with about 5dB was

confirmed (Doukovska, 2008).

Figure 7: Probability characteristics of a Hough detector

with two dimensional signal processors - adaptive CFAR

processor (API CFAR), excision binary CFAR processor

(EXC CFAR BI), binary CFAR processor (BI CFAR) and

with fixed threshold, for RAII probability - e

The most effective for noisy environment with

high probability for randomly arriving impulse

interference is the Hough detector with adaptive non

coherent CFAR signal processor (API CFAR). This

structure is by 37dB more effective than the one

with fixed threshold Hough detector (Doukovska,

2007).

5 CONCLUSIONS

In conventional signal detection approach the

process of target detection is separate from its

trajectory detection. Unlike this wide spread

technique Hough transform application allows for

simultaneous target and trajectory detection. To

detect a trajectory data from several consecutive

radar scans is processed.

The presented paper considers the results

obtained by the proposed adaptive threshold

determination procedure and analysis of different

Hough detector structures in intensive RAII

environment. The need of an adequate threshold

analysis procedure allowing better detection results

for low values of the SNR is considered.

The obtained results are applicable for wide

range of tasks like synthesis of radiolocation

detectors, communication systems, medicine and

other systems making use of infrared, ultrasonic and

other sensor types.

ACKNOWLEDGEMENTS

The investigations in this work are within the frame

of Project “Formation of Highly Qualified Young

Researchers in Information Technologies for

Optimization, Pattern Recognition and Decision

Support Systems”, Contract with the Ministry of

Education, Youth and Science: BG051PO001-

3.3.04/40/28.08.2009.

REFERENCES

Hough P. V. C., Method and means for recognizing

complex patterns, US Patent - 3,069,654, 18.XII.1962.

Carlson B., E. Evans, S. Wilson, Search Radar Detection

and Track with the Hough Transform, Parts I, II, III,

IEEE Trans., Vol. AES-30, pp. 102-124, 1994.

Akimov P., F. Evstratov, S. Zaharov, Radio Signal

Detection, Radio and Communication, Moscow, pp.

195-203, 1989 (in Russian).

Bird J., Calculating detection probabilities for systems

employing non coherent integration, IEEE Trans., vol.

AES-18, № 4, July, pp. 401-409, 1982.

Kabakchiev Chr., L. Doukovska, I. Garvanov, Hough

Radar Detectors in Conditions of Intensive Pulse

Jamming, Sensors & Transducers Magazine (S&T e-

Didest), Special Issue (ISSN 1726-5479),

“Multisensor Data and Information Processing”, №8,

pp. 381-389, 2005.

Doukovska L., Hough Detector with Binary Integration

Signal Processor, Comptes rendus de l’Academie

bulgare des Sciences, vol. 60, №5, pp. 525-533, 2007.

Doukovska L., Moving Target Hough Detector in

Randomly Arriving Impulse Interference, Cybernetics

and Information Technologies, vol. 7, №3, pp. 55-72,

2007.

Doukovska L., Hough Target Detectors with Small Values

of SNR, NATO Advanced Study Institute

“Unexploded Ordnance Detection and Mitigation”,

Poster presentation, Il Ciocco, Italy, 2008,

http://www.prometheus-inc.com/asi/uxo2008/

Doukovska L., Hough Moving Target Detector with Fixed

Threshold, Comptes rendus de l’Academie bulgare des

Sciences, vol. 61, №11, ISSN: 0861-1459, pp. 1459-

1466, 2008.

Doukovska L., Adaptive Hough Detector Threshold

Analysis in Presence of Randomly Arriving Impulse

Interference, Proc. of the International Radar

Symposium – IRS’10, Vilnius, Lithuania, pp. 142-147,

2010.

Rohling H., Radar CFAR thresholding in clutter and

multiple target situation, IEEE Trans., vol. AES-19, 4,

pp. 608-621, 1983.

APPLICATION OF MATHEMATICAL TRANSFORM IN DETECTION ALGORITHMS

167