
HYBRIDIZING ANT COLONY SYSTEMS AND TABU SEARCH FOR
A VEHICLE ROUTING PROBLEM WITH TIME WINDOWS
Juan Carlos Figueroa D., M. Ang
´
elica Pinninghoff J. and Ricardo Contreras A.
Department of Computer Science, University of Concepci
´
on, Concepci
´
on, Chile
Keywords:
Ant colony system, VRPTW, Tabu search.
Abstract:
This paper describes a new approach for solving the vehicle routing problem that considers time windows
(VRPTW). The proposal presents a hybrid approach that takes into account an ant colony system ACS and the
meta-heuristic Tabu Search. Hybridizing meta-heuristics is one of the alternatives used for solving VRPTWs.
Authors believe that a hybrid approach, with ACS providing good initial solutions for the Tabu Search heuristic
can help to get acceptable final solutions. Tabu Search plays the role of keeping diversity in the population
considered while searching a solution. The proposal was implemented and tested, and results obtained are
discussed in the final part of this presentation.
1 INTRODUCTION
The key idea concerning VRP (Toth and Vigo, 2001)
involves a routing problem with vehicles that have a
specified capacity (CVRP); this is known as a prob-
lem having multiple variables to optimize, and there-
fore, is a classical combinatorial problem. The most
popular version associated to this problem is the ve-
hicle routing problem with time windows (VRPTW),
due to his wide applicability to real problems.
All problems labeled as VRP may be described
by using a graph G defined as G = (V, A), where V =
{
0. . . n
}
is the set of nodes belonging to the graph,
and A is the set of edges that connect a specific pair
of nodes. Meta-heuristics are used to generate a set of
circuits that include the V nodes exactly once, except
one specific node that represents the starting and final
node, known as node 0 (the depot in this work).
There have been proposed different mechanisms
to deal with this problem; genetic algorithms (GA) as
in (Zhu, 2000), where authors test different crossover
operators hybridizing with hill climbing, or in (Om-
buki et al., 2006) for optimizing distances and the
number of vehicles. In (Jaszkiewicz and Kominek,
2003) the CVRP problem is presented under a genetic
algorithm approach. Finally (Berger and Barkaoui,
2004) develops a parallel GA, where a population
evolves focusing in minimizing distances.
Ant Colony System (ACO) is also used to solve
this problem. In (Tao et al., 2009) the VRPTW is
solved by combining ACO with local search algo-
rithms. Vehicles after returning to the depot can be
re-used to visit different customers if time windows
allow it. (Yu et al., 2011) deal with VRPTW com-
bining ACO and Tabu Search. We consider, when
selecting the next node in the ACS algorithm, not
only distance and pheromone, we consider the un-
used capacity in the vehicles and the waiting intervals
in time windows. Besides that, we use 2-opt search
trying to find improvements between two paths, this
is one of the differences we introduce. The objec-
tive of this proposal is to verify if hybridizing ACS
with Tabu Search allows to improve results obtained
by Solomon (Solomon, 2006).
This article is structured as follows; the first sec-
tion is made up of the present introduction; the second
section describes the problem; the third section is de-
voted to introduce the proposal, while in section four
we present some results obtained. In section five we
end with the conclusions.
2 PROBLEM DESCRIPTION
The practical problem we are interested in, that takes
as a starting point the routing vehicle problem, deals
with routing garbage trucks, a problem that presents
various objectives to optimize, such as the number of
trucks to be used, which in turn is associated to the
number of paths and the distance involved in each
469
Carlos Figueroa D. J., Angélica Pinninghoff J. M. and Contreras A. R..
HYBRIDIZING ANT COLONY SYSTEMS AND TABU SEARCH FOR A VEHICLE ROUTING PROBLEM WITH TIME WINDOWS.
DOI: 10.5220/0003701104690472
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 469-472
ISBN: 978-989-8425-95-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

path. Not less important, it is necessary to consider
the time involved in each path and constraints such
as specific (and limited) time period in which the
garbage collection can be done. The last constraint
shows that we are solving a problem that can be clas-
sified as VRPTW.
VRPTW needs to satisfy a time window defined
for a customer i as [a
i
, b
i
], which expect to accom-
plish the job in a specific time interval. The starting
time cannot be previous to a
i
and the arrival time w
i
plus the time devoted to a particular customer i can-
not exceed b
i
. The central depot, represented by 0 is
also associated to a time window, which is defined as
[E, L], where E represents the time in which the trucks
begin to traverse their routes, and L the time in which
all trucks should be in the depot. If truck k arrives to a
customer i location in a time w
i
and satisfies w
i
< a
i
,
the truck k has to wait until w
i
≥ a
i
.
A good solution optimizes (minimizes) the sum of
costs involved in the K path considered for the vehi-
cles.
The cost associated to a path for a vehicle k is de-
termined by the sum of costs c
i j
corresponding to the
edges (i, j) that belong to the path. This solution must
satisfy the following constraints:
i) A customer is visited by, exactly, one vehicle,
ii) every path has only one edge from the depot, iii)
every node in the path has only one edge arriving to
it, and only one edge starting from it, iv) every path
has only one edge arriving to the depot, v) the sum
involving the customer’s attention time for customer i
and the time involved in going from i to j needs to be
less or equal to the time in which attention for a new
customer j begins, vi) the arrival time to a customer i
location, for one vehicle, needs to be associated to the
time interval defined for customer i, vii) starting time
from the depot, and arrival time to the depot need to
be considered in the interval associated to the depot
and viii) the sum of customer’s demands, for a partic-
ular path cannot exceed the vehicle capacity.
3 THE PROPOSAL
We propose to combine ACS with Tabu Search as fol-
lows: For each iteration in ACS, once the best route is
found by an ant colony, this route is improved through
2-opt. The route obtained in this way is used as input
data for applying the meta-heuristic Tabu Search. If
Tabu Search effectively improves the solution, it is re-
introduced into the colony, just before the process of
global pheromone updating.
Ant Colony System (ACS) was proposed by
Dorigo in (Dorigo and Stuetzle, 2004). As in other
ACO algorithms, ACS is a meta-heuristics inspired
in ants’ behavior when trying to find food. In the
collaborative behavior, communication among ants is
accomplished through a pheromone trail, that is se-
creted by the ants when moving from one point to
another, and that is used to influence the ants behav-
ior that contact this chemical factor. In this particular
work, we use ACS, that is characterized for having
a local and a global mechanism for updating the se-
creted artificial pheromone, allowing a search process
in which random aspects are more relevant.
Tabu Search is a meta-heuristic algorithm that can
be used for solving combinatorial optimization prob-
lems. Tabu search uses a local or neighborhood search
procedure to iteratively move from a solution x to a
solution x
0
in the neighborhood of x, until some stop-
ping criterion has been satisfied. To explore regions
of the search space that would be left unexplored by
the global search procedure, ACS in this case, Tabu
Search modifies the neighborhood structure of each
solution as the search progresses (Glover and Laguna,
1997).
When building a solution to the VRPTW, each ant
begins their path from the depot and visits different
customers, until the capacity of the vehicle is com-
pleted. Then the ant goes back to the depot forming
a path. This process is repeated until all customers
have been visited. In this way, the solution for one ant
builds as many path as times has started a search from
the depot.
ACS features are: i) Each time an ant choose a
customer, they have the possibility of doing it in a
probabilistic or deterministic way; this possibility is
given by a parameter called q
o
. ii) Pheromone up-
dating is accomplished through a global process that
considers the best solution that has been reached until
this moment. iii) Each ant diminishes a certain quan-
tity of pheromone each time it goes through an edge,
allowing this way that future ants can explore differ-
ent paths.
In ACS, when an ant that is in node i has to select
a new node, not previously visited, from a set N(i), it
considers the quantity of pheromone and the cost of
traversing an edge (i, j), for each j ∈ N(i). Besides
that, in this proposal two additional variables as pro-
posed in (Bullnheimer et al., 1997) were considered;
the first one is the time to arrive to the customer j
location, with respect to their time window (∆v) de-
scribed in equation (1), and the second is the wasted
capacity of a vehicle (∆c) described in equation (2).
In this way equation (3) describes the mechanism an
ant uses for selecting a node j.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
470
∆v =
1, i f w
ik
= a
i
;
0, i f w
ik
> b
i
;
1
|a
i
−w
ik
|
, otherwise;
(1)
∆c =
1, i f C =
∑
i∈N
d
i
∑
j∈∆
+
(i)
x
i jk
;
0, i f C <
∑
i∈N
d
i
∑
j∈∆
+
(i)
x
i jk
;
1
|C−
∑
i∈N
d
i
∑
j∈∆
+
(i)
x
i jk
|
, otherwise;
(2)
j =
argmax
l∈N
h
i
n
τ
il
[η
il
]
β
o
, i f q ≤ q
0
;
[
τ
i j
]
α
[
η
i j
]
β
[∆v]
ζ
[∆c]
θ
∑
l∈N
h
i
[
τ
i j
]
α
[
η
i j
]
β
[∆v]
ζ
[∆c]
θ
, i f j ∈ N
h
i
, otherwise;
(3)
Where q is a random number, q
0
is the param-
eter mentioned above; τ
i j
and η
i j
are the level of
pheromone and the cost of edge (i, j), respectively.
α, β, ζ and θ are the parameters that represent the in-
fluence of each variable.
For Ant Colony System (Dorigo and Gambardella,
1997) it was established the need to get a global
pheromone updating to characterize the distance in-
volved in the solution and the number of vehicles in-
volved in this solution. This is described through the
formula 4.
τ
i j
← (1 − ρ) τ
i j
+ ρ ∗
∆τ
bs
i j
+ ∆v
bs
, (4)
Where ρ is the parameter that indicates the level
of pheromone to be updated; ∆τ
bs
i j
=
1
cost−best−solution
and ∆v
bs
=
1
vehicles−best−solution
.
The local updating of pheromone is given by
equation (5)
τ
i j
← (1 − ξ)τ
i j
+ ξτ
0
, (5)
Where 0 < ξ < 1 is the quantity of pheromone to
evaporate and τ
0
is the initial level of pheromone ini-
tially allocated to every edge.
Additionally, solutions obtained from ACS have
been improved with 2-opt, that is able to obtain re-
sults rapidly. It is due to his simple approach, intend-
ing to replace the edges under analysis by other edges
having a lower cost, and that it can be done by re-
structuring the nodes associated to those edges.
4 RESULTS
The following table shows the values for parameter
used in testing the hybrid algorithm, that were ob-
tained through experimentation.
In the table, NACS represents the number of ant’s
colonies; H represents the number of ants per colony.
Table 1: Set of parameters for ACS/2-opt.
NACS H α β ζ
10 1000 3 4 2
θ q
0
ρ ξ τ
0
1 0, 4 0, 1 0, 1 3.6724741E −6
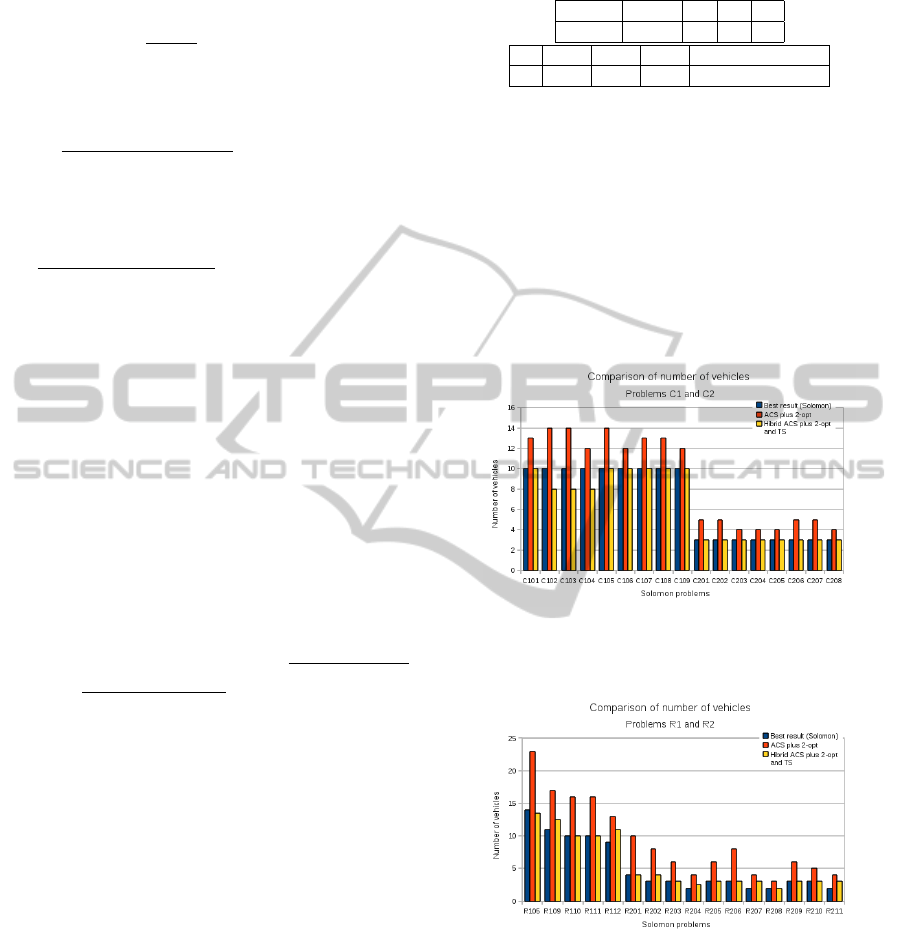
In graphics shown in figures 1 and 2, we can see
the hybrid algorithm performance that correspond to
two of the three categories proposed by Solomon.
When analyzing these graphics, it is possible to de-
duce that the proposed algorithm offers a good aver-
age behavior. The worst case corresponds to a differ-
ence of two additional vehicles for only one problem
(R112). There is a difference of (at most) one addi-
tional vehicle in some problems. For all the other in-
stances our proposal offers solutions that are similar
to solutions in Solomon.
Figure 1: Comparison of Best result, ACS/2-opt and Hybrid
approach in problems with prefix C (on the number of ve-
hicles).
Figure 2: Comparison of Best result, ACS/2-opt and Hybrid
approach in problems with prefix R (on the number of ve-
hicles).
One of the problems this approach presents, is the
distance involved in the vehicles routes, because in
some cases the distance increases. It is important to
notice that this behavior is likely to occur when cus-
tomers are grouped into clusters, having time win-
dows with large intervals.
HYBRIDIZING ANT COLONY SYSTEMS AND TABU SEARCH FOR A VEHICLE ROUTING PROBLEM WITH
TIME WINDOWS
471
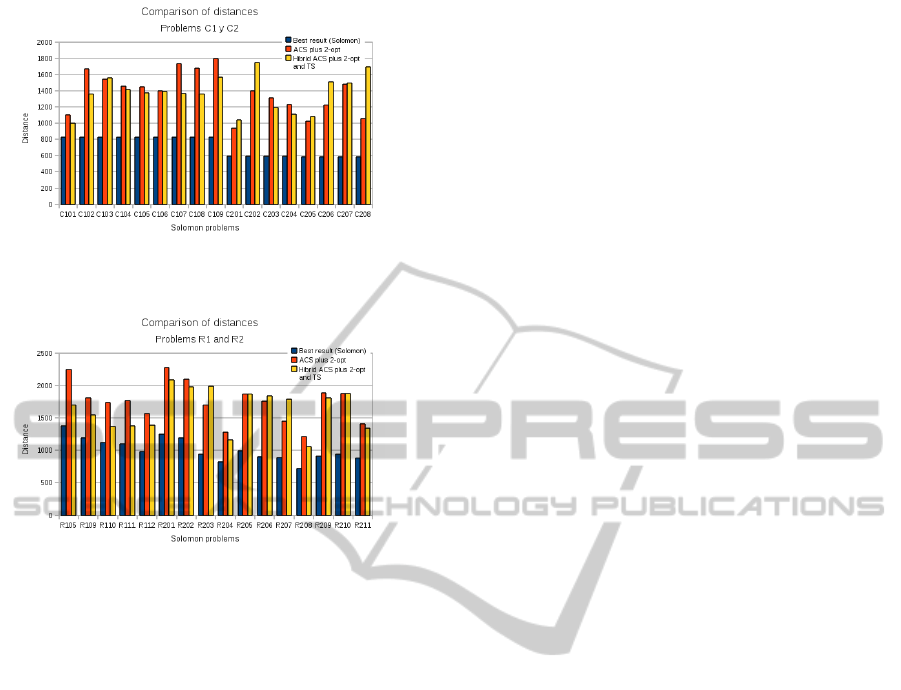
Figure 3: Comparison of Best result, ACS/2-opt and Hybrid
approach in problems with prefix C (on the distance).
Figure 4: Comparison of Best result, ACS/2-opt and Hybrid
approach in problems with prefix R (on the distance).
5 CONCLUSIONS
Hybridizing meta-heuristics appears as a promising
strategy for solving combinatorial problems; but there
is a lot of work still to be done. Results illustrate a
wide variety of cases; but it is necessary to handle
these cases carefully. On one hand, we got good re-
sults in the case of specific instances, but in most of
other instances results were definitely poor.
Solomon, on the other hand, presents academic
examples, that not necessarily reflect a real city cus-
tomer distribution. The euclidean computation of the
distances should be probably replaced by a Manhattan
distance computation. In the same sense, the random
distribution of customers in a city doesn’t reflect, in
most of cases, a real city.
However, the basic idea of combining different
mechanism that provides, from their own features,
promising pre-processed solutions is something that
should be explored more deeply.
REFERENCES
Berger, J. and Barkaoui, M. (2004). A parallel hybrid ge-
netic algorithm for the vehicle routing problem with
time windows. Computers and Operation Research,
31:2037–2053.
Bullnheimer, B., Hartl, R., and Strauss, C. (1997). Ap-
plying the ant system to the vehicle routing problem.
In Proceedings of the Second Metaheuristic Interna-
tional Conference.
Dorigo, M. and Gambardella, L. (1997). Ant colony sys-
tem: a cooperative learning approach to the traveling
salesman problem. IEEE Transactions on Evolution-
ary Computation.
Dorigo, M. and Stuetzle, T. (2004). Ant Colony Optimiza-
tion. Bradford Book.
Glover, F. and Laguna, M. (1997). Tabu search. Springer.
Jaszkiewicz, A. and Kominek, P. (2003). Genetic local
search with distance preserving recombination oper-
ator for a vehicle routing problem. European Journal
of Operational Research, 151(2):352–364.
Ombuki, B., Ross, B. J., and Hanshar, F. (2006). Multi-
objective genetic algorithm for vehicle routing prob-
lems with time windows. Applied Intelligence,
24(1):17–30.
Solomon, M. (2006). Benchmark problems.
http://www.sintef.no/ Projectweb/ TOP/ Problems/
VRPTW/ Solomon-benchmark/, [Online; accessed
09-July-2010].
Tao, Z., Song, S., and Yue-Jie, Z. (2009). H-aco algo-
rithms for the vrptw with re-used vehicles. Interna-
tional Conference Measuring Technology and Mecha-
tronics Automation.
Toth, P. and Vigo, D., editors (2001). The vehicle routing
problem. Society for Industrial and Applied Mathe-
matics.
Yu, B., Yang, Z. Z., and Yao, B. Z. (2011). A hybrid algo-
rithm for vehicle routing problem with time windows.
Expert Systems with Applications, (33):435–441.
Zhu, K. Q. (2000). A new genetic algorithm for vrptw. Pro-
ceedings of the International Conference on Artificial
Intelligence, page 311264.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
472
