
AN EXPERT SYSTEM MODEL IN PSYCHIATRY FOR CASE
FORMULATION AND TREATMENT DECISION SUPPORT
Irosh Fernando
1
, Frans Henskens
1
and Martin Cohen
2
1
School of Electrical Engineering & Computer Science, University of Newcastle, Callaghan, NSW 2308, Australia
2
The Mater Hospital, Edith St, Waratah, NSW 2298, Australia
Keywords: Expert systems in psychiatry, Psychiatric case formulation, Treatment decision support, Artificial
intelligence in medicine.
Abstract: Whilst case formulation is a critical task in psychiatry, it is an unexplored area in the field of medical expert
systems development, which has mostly focused on the diagnostic inference. Case formulation plays a more
important role in planning, and individualising treatments compared to categorical diagnoses. Nevertheless,
case formulation is considered to be challenging task even for clinicians due to the highly subjective nature
of the psychiatric knowledge, and lack of defined criteria, which are available for diagnoses. Lack of
conceptual model, which captures the depth and the complexity of the clinical knowledge and reasoning
demonstrated by expert clinicians, is considered to be a one of the root causes of failures in previous
approaches. Whilst the authors have described a conceptual model for diagnostic consultation in a separate
paper, this paper describes the conceptual model for case formulation and treatment decision support, thus
laying down a domain-specific theoretical foundation required for successful implementation of expert
systems in psychiatry. The knowledgebase has been conceptualised as a hierarchically organised set of
entities spanning the domains of diagnostic knowledge, etiological knowledge and treatment knowledge,
through which an iterative inference is made using the logical inferences of abduction, deduction and
induction.
1 INTRODUCTION
Case formulation is considered to be a crucial task in
psychiatric assessments. It requires high level skills
and knowledge, and is typically a key aspect of
assessment in specialist examinations in psychiatry.
When a patient is being assessed, case formulation is
important because it provides the core framework
for cohesive integration of the clinical knowledge,
and directs clinicians towards the most appropriate
treatment(s). Poorly constructed case formulation
may result in poorly focussed consideration of the
patient’s main clinical issues, perhaps leading to
sub-optimal or even inappropriate treatment
decisions, which may adversely affect the patient.
Whilst case formulation is such an important task, it
is often considered to be too challenging,
particularly for junior clinicians (McDermott et al.,
1996), (Mellsop and Banzato, 2006). As a
foundation for this research work, the authors have
introduced a systematic method for developing
psychiatric case formulation for clinicians (Fernando
et al., 2011).
Because they are two parallel processes that
utilise a common data set (i.e. clinical symptoms and
the patient history) in psychiatric assessment, case
formulation and making diagnoses are closely
related. Whilst diagnoses are categorical and
generic, case formulation provides a
conceptualisation to closely understand the unique
circumstances of the individual. Therefore, case
formulation is extremely important in developing an
individualised treatment plan. Nevertheless, case
formulation is an unexplored area in the field of
expert systems development, and the small number
of psychiatry expert systems (e.g. DUNE (Hardt and
MacFadden, 1987)) described in the literature
mainly address diagnostic consultations. The authors
have already introduced a conceptual model for
diagnostic consultation in psychiatry (Fernando et
al., 2011). This paper expands on the conceptual
model to encompass case formulation and treatment
decisions, thereby laying down a complete
329
Fernando I., Henskens F. and Cohen M..
AN EXPERT SYSTEM MODEL IN PSYCHIATRY FOR CASE FORMULATION AND TREATMENT DECISION SUPPORT.
DOI: 10.5220/0003701903290336
In Proceedings of the International Conference on Health Informatics (HEALTHINF-2012), pages 329-336
ISBN: 978-989-8425-88-1
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

theoretical framework for building expert systems in
psychiatry, and for future research.
We believe medical expert system development
in general faces a number of challenges in relation to
the domains of conceptual modelling,
implementation, and social and organisational
aspects. The main problems of the previous
approaches(e.g. INTERNIS-1/ CADUCEUS
(Wolfram, 1995); (Miller, 1984); CADIAG-1 and
CADIAG-2 (Adlassnig and Kolarzs, 1986);
Parsimonious Covering Theory (Reggia and Peng,
1987); A Process Model of Diagnostic Reasoning
(Stausberg and Person, 1999) to development of
medical expert systems include: failure to develop
conceptual models that capture the depth of the
domain; difficulties in developing a sufficiently
large knowledgebase; and failure to take into
consideration the social and organisational issues
related to operational aspects of the implemented
system. The authors have discussed these aspects in
a separate paper (including the limitations of the
previous approaches), and have proposed a
development framework in order to overcome these
challenges (Fernando et al., 2011). The very first
step towards developing a successful medical expert
system is developing a conceptual model that
captures the depth and the complexity of clinical
reasoning in specialised medical domains. This
paper and the previous one attempt to achieve this
first step, specifically in the field of psychiatry.
2 KNOWLEDGEBASE MODEL
The key to successful clinical inference is the
structure of the knowledgebase. Whilst there are
approaches in which the knowledgebase is
independent from the inference process (e.g.
CLASSIKA (Gappa et al., 1993), PROTÉGÉ (Tu et
al., 1995), such approaches are deemed unsuitable
for a highly specialised knowledge domain such as
psychiatry, in which the inference mechanism is
dependent on the knowledgebase structure from the
clinician’s perspective.
The knowledgebase encompasses three domains:
diagnostic knowledge; etiological knowledge; and
the treatment knowledge, which may be organized
as a hierarchy as described in Figure-1. The
diagnostic domain of the knowledgebase consists of
layers representing respectively individual
symptoms, and clinical phenomena, in which
symptoms combine to form unique clinical
phenomena. The etiological domain of the
knowledgebase consists of layers representing
respectively model concepts, and explanatory
models, which can be derived from a number of
etiological theories in psychiatry including ego-
psychology (Freud 1923); self-psychology (Kohut,
2009); object-relations theory (Ogden, 1983);
attachment theory (Bowlby, 1969); cognitive
schema therapy model (Young et al., 2003); and
Interpersonal Therapy Model (Weissman et al.,
2000). Each explanatory model consists of a unique
combination of model concepts. Each clinical
phenomenon is related to one or more model
concepts, thus bridging the diagnostic domain and
the etiological domain of the knowledgebase. The
treatment domain consists of layers representing
respectively treatment components, and individual
treatments. Each treatment comprises a unique
combination of treatment components. Figure-2
explains the knowledgebase model using an
example, in which the two symptoms “low self-
confidence” and “oversensitivity to criticism” along
with several other symptoms form the clinical
phenomenon “Low self-esteem”. Next, this clinical
phenomenon is related to the model concept,
“Cognitive schema of defective self” in the
etiological knowledge domain. One explanatory
model is shown in the next layer of the etiological
knowledgebase, and it is made up of three model
concepts: “Predisposing events”, “Cognitive schema
of defective self” and “Precipitating events”. This
explanatory model is related to the treatment
component “Cognitive Re-structuring” in the
treatment knowledge domain, which happens to be a
part of the treatment “Cognitive Behaviour
Therapy”. The clinical basis of this structure of the
knowledgebase is not within the scope of this paper
and is covered elsewhere (Fernando et al., 2011).
Clinical phenomena are made up of a
constellation of symptoms, and arguably play a more
critical role in clinical reasoning in psychiatry
compared to other branches of medicine. They are
directly related to phenomenological concepts in
psychiatry, and can be considered as core clinical
features or recurrent themes in clinical scenarios.
Diagnostic inference based on clinical phenomena is
considered to have more reliability and validity
compared to that based on symptoms, since each
clinical phenomenon is a unique constellation of a
number of clinical symptoms.
The main components of the diagnostic
knowledgebase and their relations are defined as
follows.
={
,
,…,
} is the set of all symptoms.
ℎ={
,
,…,
} is the set of all clinical
phenomena.
HEALTHINF 2012 - International Conference on Health Informatics
330
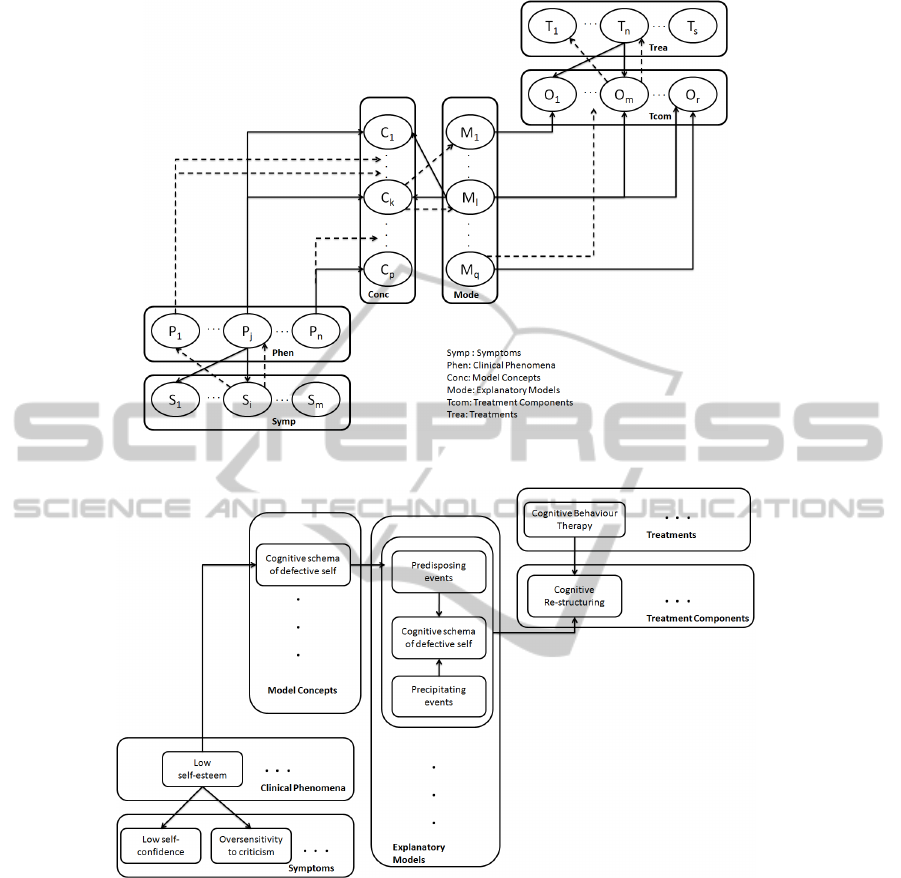
Figure 1: Hierarchical model of the three clusters of knowledge.
Figure 2: An example using the knowledgebase model.
⊆ℎ ×=
ℎ
∈
ℎ,
∈.
=
|
∈
∀
∈ℎ
is the set of all symptoms related to a clinical
phenomenon
.
:→[0,1] is a function where
(
)
indicates the degree of severity of the symptom,
on a scale from 0-1( i.e.
(
)
=0 ⟹ the severity
of the symptom
is minimum, whereas
(
)
=1
⟹ the severity of the symptom
is maximum).
:ℎ→[0,1] is a function where
(
)
indicates the degree of confirmation of the clinical
phenomenon
in a scale from 0-1( i.e.
(
)
=
0 ⟹ the clinical phenomenon
is least likely to be
confirmed, whereas
(
)
=1 ⟹ the clinical
phenomenon
is most likely to be confirmed).
:
[
0,1
]
→
[
0,1
]
,ℎ
=
(
)
,
∈
is a function which determines the degree of
confirmation of the clinical phenomenon,
based
on the severity of the symptom,
.
(
)
∧
(
)
∧…∧
(
)
⟹
AN EXPERT SYSTEM MODEL IN PSYCHIATRY FOR CASE FORMULATION AND TREATMENT DECISION
SUPPORT
331

=
(
)
∈
⟹
is a rule that calculate the degree of confirmation of
the clinical phenomenon,
based on the collective
severities of the related symptoms,
,
,…,
using the following formula.
=
1
(
)
Case formulation is mainly constructed using the
etiological knowledge, which bridges the diagnostic
knowledge and treatment knowledge. Whilst there
are operationalised and defined diagnostic criteria,
which can be used during diagnostic reasoning, such
explicit rules are non-existing for psychiatric case
formulation. On the other hand, case formulation is
more complex since there can be many alternative
case formulations derived from different theoretical
orientations( as described above) causing ambiguity.
As a solution the authors have introduced an
approach to systematically organise this knowledge
and derive patterns using templates(Fernando et al.,
2011).
The main components and their relations to the
aetiological knowledgebase and the diagnostic
knowledgebase can be defined as follows.
={
,
,…,
,…,
} is the set of all model
concepts and explanatory models.
={
,
,…,
,…,
} is the set of all
explanatory models.
⊆ ×=
ℎ
∈
,
∈ is the relation between the above
two sets.
=
∈
∀
∈ is
the set of all model concepts associated with a given
explanatory model,
.
⊆ℎ ×=
ℎ
∈
ℎ,
∈ is the relation between the
respective sets of clinical phenomena and model
concepts.
=
∈
∀
∈ℎ is the
set of all model concepts associated with a given
clinical phenomenon,
.
(
)
=
,∀
∈
defines that
the degree of confirmation of any model concept,
associated with the clinical phenomenon
, is the
same as the severity of
.
(
(
)
>
)
∧
(
(
)
>
)
∧…
∧
(
(
)
>
)
⟹
=
(
(
)
>
)
⟹
,
∈
is a rule to determine the strength( i.e. explanatory
power ) of a given explanatory model,
using each
of its model concepts,
of which the degree of
confirmation should be above a threshold value,
for the explanatory model to be substantiated. Given
that this rule is satisfied, the strength of the model
can be calculated as,
=
(
)
: →, ℎ
=
(
) is a
function that maps any given model concept
to its
corresponding model concept,
.
Psychiatric treatments include pharmacological and
physical interventions, psychological interventions,
and social interventions. Each treatment intervention
can be conceptualised as having several treatment
components. Whilst a single treatment intervention
is more general in relation to a particular psychiatric
diagnosis and the patient, its components are more
specific (i.e. some components are more relevant
and applicable than others). One main advantage of
this conceptualisation is that it enables the clinician
to individualise treatment. Each treatment
intervention is also associated with a set of
favourable factors, unfavourable factors, and contra
indications, which have to be evaluated against each
patient’s circumstances. For example, if a treatment
intervention is causing weight gain as a side effect,
then it is considered to be an unfavourable factor for
a patient who is already obese; a side effect of
sedation is considered to be a favourable factor for a
patient who is having sleep difficulties. On the other
hand, contra indications imply that the treatment
intervention should not be prescribed for the patient,
who has a condition that contra indicates the
intervention ( e.g. Electroconvulsive therapy is
contra indicated for a patient with elevated
intracranial pressure).
The components of the treatment knowledge,
their properties, and relations with the etiological
knowledge can be defined as follows.
={
,
,…,
,…,
} is the set of all
treatment components.
={
,
,…,
,…,
} is the set of all
available treatments.
⊆ × =
ℎ
∈
,
∈ is the relation between the above
sets of treatments and treatment components.
HEALTHINF 2012 - International Conference on Health Informatics
332

=
∈
∀
∈ is the
set of all treatment components associated with a
given treatment,
.
⊆ ×=
ℎ
∈
,
∈ is the relation between the two
sets, explanatory models and treatment components.
=
∈
∀
∈ is
the set of all treatment components associated with a
given explanatory model,
.
:
→[0,1] is a function where
(
)
indicates the effect size of the treatment
component,
for the explanatory model,
, on a
scale from 0-1( i.e.
(
)
=0 ⟹ the effect size of
is minimum, whereas
(
)
=1 ⟹ the effect
size of
is maximum).
ℎ
>
⟹
|
ℎ
(
|
) is a rule that indicates
the effect size of the treatment component
for the
clinical phenomenon
, which has a degree of
confirmation above the threshold value,
, and is
associated with the explanatory model
via the
model concept,
.
={
,
,…,
} is the set of favourable
factors associated with treatment,
.
={
,
,…,
} is the set of
unfavourable factors associated with treatment,
.
={
,
,…,
} is the set of
contraindications for treatment,
.
:{
∪
}→[0,1] is a function
that quantifies the degree of the favourable factors,
and of the unfavourable factors.
The favourable factors, unfavourable factors and the
contraindications can be expressed using the
following generic form of inference rule.
(
)
∧
(
)
∧…∧
(
)
⟹
where,
=
(
is the weight assigned to the favourable factor,
according to its importance).
Similarly,
(
)
∧
(
)
∧…∧
(
)
⟹
where,
=
(
is the weight assigned to the unfavourable
factor,
according to its significance).
On the other hand, contraindications do not require
quantification, and can be expressed in the following
form of generic inference rule.
⋁
⋁…⋁
⟹ ¬
,which indicates that if any
of the contraindications are present, the treatment,
should not be prescribed.
3 INFERENCE MODEL
As in the case of diagnostic consultation that has
been covered elsewhere (Fernando, Henskens et al.
2011), we adopted the ST-model (Ramoni, Stefanelli
et al. 1992), which provides a sound framework
based on the logical inferences of abduction,
deduction and induction described by Charles Peirce
(Peirce 1878). There are other reasoning strategies
described in the literature (e.g. Hypothetico-
deductive reasoning (Elstein et al., 1978); Pattern
recognition and categorisation (Norman et al.,
1992); Inductive and Scheme-inductive reasoning
(Mandin et al., 1997); Forward and Backward
reasoning (Hunt, 1989), (Patel and Groen, 1986)),
but they are not as comprehensive as the ST- Model.
The clinical inference involves an iterative process
of three stages: abstraction; abduction; and
deduction, leading to the induction stage.
3.1 Abstraction
Patients report their symptoms and disclose their
history using their own terminology and language,
whereas the components of the knowledgebase are
specific concepts defined in the clinician’s mind.
Abstraction involves the process of substantiating
these concepts (i.e. symptoms, clinical phenomena,
model concepts, models) by mapping what patients
report into them. For example, a patient might report
“having a dark cloud over me”, which will turn out
to be abstracted as the symptom “depressed mood”.
Abstraction also involves determining the severity of
each symptom,
and determining the degree of
confirmation of each clinical phenomena,
based
on the functional relationship,
, which is a
mathematical function approximated using the
expert clinical judgement ( an example is given in
Figure-3).
AN EXPERT SYSTEM MODEL IN PSYCHIATRY FOR CASE FORMULATION AND TREATMENT DECISION
SUPPORT
333
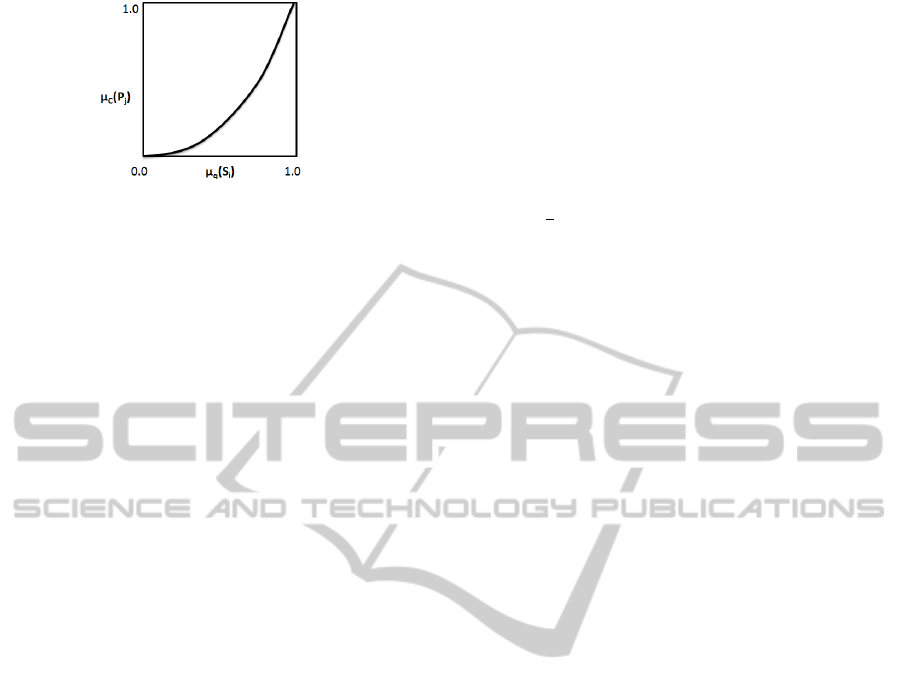
Figure 3: An example of the functional relationship
between
(
)
and
.
3.2 Abduction
After a symptom,
is substantiated via abstraction,
abduction involves generating hypotheses, which
indicates the likely clinical phenomena associated
with
. Next, once a clinical phenomenon,
is
substantiated (which also involves deduction and
induction as described in following sections),
abduction involves hypothesising the likely
explanatory models. Similarly, once an explanatory
model,
is substantiated, abduction involves
hypothesising the possible treatment components
indicated for
.
For example, consider the following two
inference rules, in which
are included in the
antecedent.
(
)
∧
(
)
∧
(
)
⟹
(
)
∧
(
)
∧
(
)
⟹
(
)
Once the degree of severity of
is determined,
abduction involves hypothesising the clinical
phenomena
and
, which, then, requires
deductive inference as explained in the next section.
Once,
and
(
)
are determined, abduction
will infer the related model concepts, explanatory
models, treatment components, and treatments in a
similar manner. The direction of the abduction
inference is bottom-up as indicated by the broken
lines in Figure-1.
Abduction may involves generating a very large
number of hypotheses, which may leads to an
unacceptably lengthy inference cycle, impacting on
efficiency. Strategies including prioritising the
hypotheses, and using pattern recognition, and
exclusion and inclusion criteria to narrow down the
range of hypotheses have been discussed
elsewhere(Fernando, Henskens et al. 2011).
3.3 Deduction
For each hypothesis generated during abduction,
deduction involves exploring further information
with the aim of confirming or rejecting the
hypothesis. For example, as described under the
above section, consider that the clinical phenomenon
is hypothesised via abduction based on the
symptom
. Next, deduction involves eliciting
symptoms
and
via abstraction, inferring
(
)
and
(
)
, and finally, calculating
as follows.
=
(
)
+
(
)
+
(
)
where
is the function, that
describes the relationship between the severity of the
symptom
denoted by
(
)
and the degree of
the confirmation of the clinical phenomenon,
denoted by
. Similarly
is the function, that
describes the relationship between
(
)
and
;
is the function, that describes the
relationship between
(
)
and
.
Similarly, for each explanatory model hypothesised,
deduction involves exploring the rest of the model
concepts, and therefore related clinical phenomena
included in similar inference rules.
In relation to the process of making treatment
decisions, deduction involves exploring
contraindications, and favourable factors associated
with each hypothesised treatment component, and
treatment. For example, consider the following
inference rules for favourable factors, unfavourable
factors, and contraindications for the treatment,
which has been hypothesised.
∧
∧…∧
⟹
∧
∧…∧
⟹
⋁
⋁…⋁
⟹ ¬
Deduction involves exploring the presence of any of
the favourable factors,
,
,…,
; unfavourable
factors
,
,…,
; and the
contraindications
,
,…,
.
The direction of the deductive inference is the
reverse of the abductive inference (i.e. top-down) as
indicated by solid lines in Figure-1.
3.4 Induction
Inductive inference ends the iterative inference
cycle, and involves accepting or rejecting the
generated hypotheses using the information gathered
during the previous stages, by matching them with
the inference rules. For example, given the inference
rule involving model concepts,
(
(
)
>
)
∧
(
(
)
>
)
∧
(
(
)
>
)
⟹
,
and
(
)
>
,
(
)
>
and
(
)
>
HEALTHINF 2012 - International Conference on Health Informatics
334

then the explanatory model
would be confirmed
with a strength of
.
Deciding the best treatment, involves calculating
the effect size and then the suitability of each
treatment using the following formula.
=
1
(
|
)
, ∀
∈
, ∀
∈
(
)
,
which calculates the effect size of the treatment,
by taking the average value of the total sum of the
maximum effect size related to each pair of its
treatment component and explanatory model.
For example, consider the patient’s clinical
phenomena are explained by three explanatory
models,
,
and
, each of which is paired with
three different treatment components
,
and
as follows:
|
,
|
,
|
,
|
,
|
and
|
. Suppose that the effect-size of these
tuples are respectively
(
|
)
=0.4;
(
|
)
=0.6;
(
|
)
=0.8;
(
|
)
=0.2;
(
|
)
=0.3;
(
|
)
=0.7.
Now, consider that there are two treatments,
and
which are paired with the treatment
components as follows:
|
,
|
and
|
,
|
Determining
whether treatment,
or
has the higher effect size
involves the following calculations:
(
)
=
1
2
(
(
|
)
,
(
|
)
)
+
(
(
(
|
)
,
|
)
,
(
|
)
)
=
1
2
(
0.6,0.8
)
+
(
0.4,0.3,0.7
)
=
1
2
(
0.8 + 0.7
)
=0.75
(
)
=
1
2
(
(
(
|
)
,
(
|
)
)
+ (
(
|
)
)
)
=
1
2
(
0.6,0.8
)
+
(
0.2
)
=
1
2
(
0.8 + 0.2
)
=0.5
Therefore
has the higher effect-size.
Next, the overall suitability of a given
treatment,
is calculated based on the effect size
and the cumulative effect of favourable and
unfavourable factors, using the formula,
=
−
4 CONCLUSIONS
Medical expert systems have not progressed much
after an initial golden era several decades ago. The
authors have identified a number of reasons related
to developing conceptual and computational models,
their implementations and social issues. The root
cause of the failure, however, is related to the
difficulty of capturing the depth and the complexity
of broader clinical reasoning (involving all three
aspects of diagnostic assessment, etiological
formulation and treatment decisions) exhibited by
expert clinicians. A further problem involves that of
engrossing the expert’s reasoning in a conceptual
model, when knowledge engineers do not have the
necessary medical background. Additionally,
generic medical expert system models are
unsuitable, since there are significant differences in
relation to the nature of the domain knowledge and
the inference strategies used in different medical
specialties. Furthermore, the inference mechanism is
dependent on the structure of the knowledgebase.
As a new approach, the authors have proposed a
conceptual model for developing a domain-specific
expert system in psychiatry. This paper addresses
etiological reasoning, which involves case
formulation, and treatment decisions in psychiatry;
the authors previously addressed the issue of
diagnostic reasoning in a separate and
complementary paper (Fernando et al., 2011). The
pair of papers thus completely cover the broader
aspects of clinical reasoning in psychiatry.
Importantly, whilst the crucial role of case
formulation in psychiatry has been previously
recognised, we have for the first time modeled case
formulation in a way that can be implemented in
psychiatry-specific expert systems. Whilst this
conceptual model will undoubtedly be subject to
future revision and refinement, it completes the first
step required for developing successful expert
system applications. Finally, it is expected that the
theoretical foundation described here will provide
insight to development of expert systems in other
medical specialties.
REFERENCES
Adlassnig, K.-P. and G. Kolarzs, (1986). "Representation
and Semiautomatic Acquisition of Medical
Knowledge in CADlAG-1 and CADIAG-2."
Computers and Biomedical Research 19: 63-79.
Bowlby, J., (1969). Attachment and loss, Vol 1:
Attachment, London: Hogarth.
AN EXPERT SYSTEM MODEL IN PSYCHIATRY FOR CASE FORMULATION AND TREATMENT DECISION
SUPPORT
335

D. A. Wolfram, (1995). "An appraisal of INTERNIST-I "
Artificial Intelligence in Medicine 7: 93-116.
Elstein, A. S., L. S. Shulman, et al., (1978). Medical
Problem-Solving: an Analysis of Clinical Reasoning,
Cambridge, MA: Harvard University Press
Fernando, I., M. Cohen, et al., (2011). "Pattern-based
formulation: a methodology for psychiatric
formulation." Submitted and under revision for
Australasian Psychiatry Journal.
Fernando, I., F. Henskens, et al., (2011). A Domain
Specific Conceptual Model for a Medical Expert
System in Psychiatry, and a Development Framework.
IADIS e-Health 2011 International Conference,
Rome,Italy.
Fernando, I., F. Henskens, et al., (2011). A Domain
Specific Expert System Model for Diagnostic
Consultation in Psychiatry. 12th ACIS International
Conference on Software Engineering, Artificial
Intelligence, Networking and Parallel/Distributed
Computing (SNPD 2011), IEEE.
Freud, S. (1923). "The Ego and the Id. The Standard
Edition of the Complete Psychological Works of
Sigmund Freud, Vol 19, Translated and edited by
Strachey J. London, Hogarth Press, 1961."
Gappa, U., F. Puppe, et al. (1993). "Graphical knowledge
acquisition for medical diagnostic expert systems "
Artificial Intelligence in Medicine 5(3): 185-211.
Hardt, S. L. and D. H. MacFadden (1987). "Computer
Assisted Psychiatric Diagnosis: Experiments in
Software Design." Comput.Biol.Med. 17(4): 229-237.
Hunt, E. (1989). "Cognitive Science: Definition, Status,
and Questions " Annual Review of psychology 40: 603-
629
Kohut, H. (2009). The Analysis of the Self: A Systematic
Approach to the Psychoanalytic Treatment of
Narcissistic Personality Disorders, University of
Chicago Press.
Mandin, H., A. Jones, et al. (1997). "Helping students
learn to think like experts when solving clinical
problems." Academic Medicine 72: 173-179.
McDermott, J., Jr, J. Streltzer, et al. (1996). "Pilot study of
explicit grading criteria in the American Board of
Psychiatry and Neurology. Part II. Examination." Am J
Psychiatry 153(8): 1097-1099.
Mellsop, G. W. and C. E. M. Banzato (2006). "A Concise
Conceptualization of Formulation." Acad Psychiatry
30(5): 424-425.
Norman, G. R., C. L. Coblentz, et al. (1992). "Expertise in
visual diagnosis - a review of the literature." Academic
Medicine 66(suppl): s78-s83.
Ogden, T. H. (1983). "The concept of internal object
relations. International Journal of Psychoanalysis."
64: 227-241.
Patel, V. L. and G. J. Groen (1986). "Knowledge based
solution strategies in medical reasoning." Cognitive
Science 10(1): 91-116.
Peirce, C. S. (1878). "Illustrations of the logic of science,
sixth paper-deduction, induction, hypothesis."
The
Popular Science Monthly 1: 470-482.
R. A. Miller, (1984). "INTERNIST-I/CADUCEUS:
problems facing expert consultant programs." Methods
Inf Med. 23(1): 9-14.
Ramoni, M., M. Stefanelli, et al., (1992). "An
epistemological framework for medical knowledge-
based systems" IEEE Transactions on Systems, Man
and Cybernetics 22(6): 1361 - 1375.
Reggia, J. A. and Y. Peng, (1987). "Modeling diagnostic
reasoning: a summary of parsimonious covering
theory." Computer Methods and Programs in
Biomedicine 25: 125-134.
Stausberg, J. R. and M. Person, (1999). "A process model
of diagnostic reasoning in medicine." International
Journal of Medical Informatics 54: 9-23.
Tu, S. W., H. Eriksson, et al., (1995). "Ontology-based
configuration of problem-solving methods and
generation of knowledge-acquisition tools: application
of PROTE´GE´ -II to protocol-based decision
support." Artificial Intelligence in Medicine 7: 257-
289.
Weissman, M. M., J. C. Markowitz, et al., (2000).
Comprehensive guide to interpersonal psychotherapy,
Basic Books.
Young, J. E., J. S. Klosko et al., (2003). Schema therapy:a
practitioner's guide, Guilford Press.
HEALTHINF 2012 - International Conference on Health Informatics
336
