
RELIABILITY OF STATISTICAL FEATURES
DESCRIBING NEURAL SPIKE TRAINS
IN THE PRESENCE OF CLASSIFICATION ERRORS
Ninah Koolen, Ivan Gligorijevic and Sabine Van Huffel
Department of Electrical Engineering (ESAT), Division SCD, and IBBT Future Health Department,
Katholieke Universiteit Leuven, Kasteelpark Arenberg 10, box 2446, 3001 Leuven, Belgium
Keywords: Neural Activity, Spikes, Spike Clustering, Statistical Parameters.
Abstract: In order to investigate functioning of the brain processes, it is important to have reliable processing of
neural activity. For precise tracking of local neural network processes, reliable clustering of single neurons’
action potentials (spikes) is necessary. So far, it was common to keep the signals of high quality and discard
the others. This work examines the possibility of extracting reliable information from bad quality signals, in
the presence of spike classification errors. We tested the robustness and information capacity of several
statistical parameters used to describe firing patterns of spike trains using simulated signals mimicking most
common cases in nature. Although complete reconstruction of firing patterns is not always possible, we
show that the approximation of the mean firing frequency as well as the detection of bursting processes can
still be quantified successfully, thereby paving the way for future applications.
1 INTRODUCTION
To extract the useful information about the condition
and changes in functioning of a region in the brain,
appropriate processing of neuronal signal recordings
is a crucial step (Chan et al., 2010).
Neurons are the foundation of our nervous
system. They are the transmitters of all the
information in our nervous system through electrical
and chemical signaling. Information processed in the
brain is embedded in neuronal spikes which are all-
or-none binary processes. By observing “firing”
patterns of some neurons by means of extracellular
recordings, we are able to get a glimpse on general
conditions in the observed area. It is common
practice to keep the signals of high quality in terms
of signal-to-noise ratio (SNR) and discard the others.
However, more high quality signals usually implies
more recording places, which means bigger damage
of the tissue during electrode placement and so on. It
is therefore useful to maximize the value of
extracted information if possible by processing even
low quality signals.
We investigate the robustness of certain statistical
parameters used to describe firing patterns of
neurons when the quality of the signal and the spike
classification is low. In order to detect and assign
spikes to their firing neurons, we apply the well-
known Wave_clus spike clustering algorithm
(Quiroga et al., 2004). We then continue and
generalize our approach so that arbitrary clustering
algorithm can be used. We assume and vary a
certain percentage of wrongly classified spike
appearance times (timestamps) and observe the
results in terms of errors of statistical parameters
used to describe spike trains.
Using artificial signals with realistic distributions,
with known underlying values of parameters, we
show how to assess the information carrying
capacity of each of them as well as their robustness.
Standard parameters (mean, median, burst
coefficient, coefficient of variation, skewness,
kurtosis etc.) are used. In addition new parameters
are also introduced.
2 METHODOLOGY
2.1 Artificially Generated Distributions
and Signals
Since real data’s underlying distribution of spike
169
Koolen N., Gligorijevic I. and Van Huffel S..
RELIABILITY OF STATISTICAL FEATURES DESCRIBING NEURAL SPIKE TRAINS IN THE PRESENCE OF CLASSIFICATION ERRORS.
DOI: 10.5220/0003702501690173
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2012), pages 169-173
ISBN: 978-989-8425-89-8
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
timestamps is unknown, artificially generated
signals were used in this study. These served as
input to the clustering algorithm and for later
statistical parameter estimation. In this way, the true
values of parameters describing the underlying
distribution can be compared to those obtained after
detection and clustering.
We used spike shapes obtained from real
recordings, some of them available on the internet
(Rutishauser, 2011) and some obtained from IMEC -
Belgium recordings. Some examples used in this
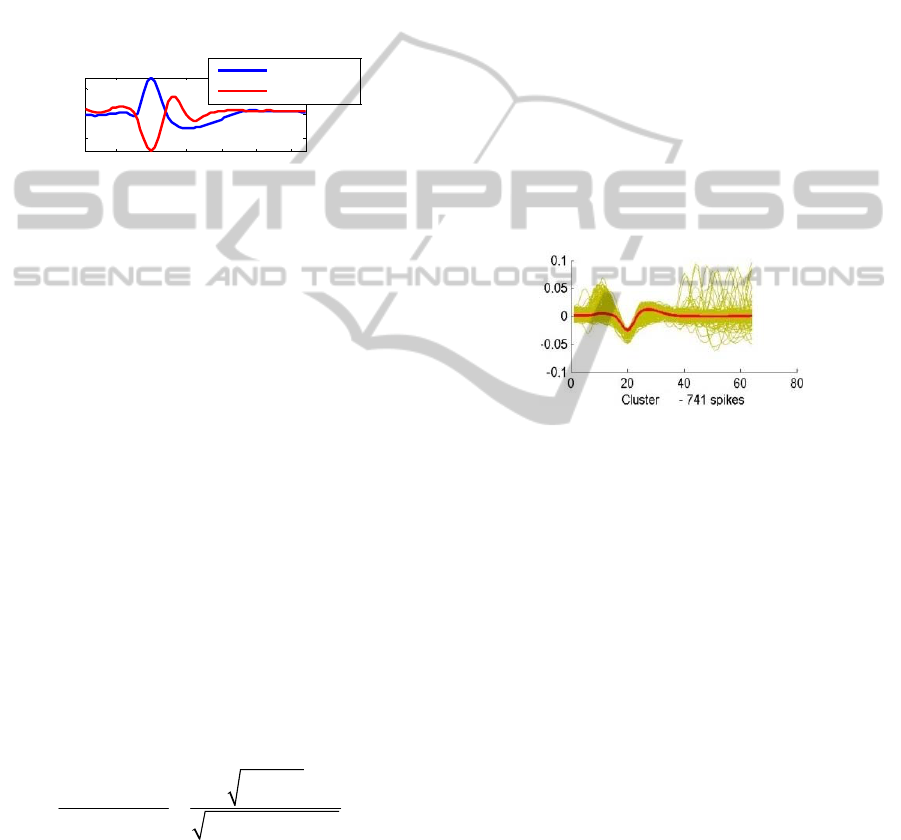
research are shown in Figure 1.
Figure 1: Two examples of spike shapes used here.
Matlab was used to generate normally and
Poisson distributed timestamps. These are reported
to be realistic models to describe the firing pattern of
a neuron (e.g. Dayan and Abbott, 2005). Also, a
simulated distribution of a firing pattern containing
bursts (fast consecutive neural firing) was created. A
neuron is bursting if it is firing consecutive spikes
with very small intermediate break intervals (< 3
ms). Signals are created by adding spikes whenever
indicated by created timestamps. Noise is also added
to form a realistic artificial neuronal signal. This
noise is a mixture of white noise and background
noise. The latter consists of a large number of
randomly selected and scaled waveforms which
were added to mimic far away neurons (Rutishauser
et al., 2006). The SNR is differed among those
artificial signals (calculated as in formula 1 with n
the number of samples of a selected spike). To
create different low quality signals, this random
noise trace can be rescaled to obtain signals with a
pre-specified SNR. Overall, around 120 signals were
used in this study.
(1)
A more general and computationally faster
procedure avoiding the need for the clustering is also
applied. This procedure simulates classification
errors by mixing timestamps of multiple spike trains.
A certain percentage of these timestamps, imposed
by the user, is correctly classified; accordingly,
misclassified (assigned to a wrong cluster)
timestamps are added as well. In addition, a certain
percentage of timestamps is left undetected to
imitate the realistic case, where some spikes evade
detection because of low SNR. The computational
gain is achieved by mimicking the clustering results
without applying the actual procedure. After
assigning timestamps to clusters, robustness of
parameters is tested.
2.2 Robustness of Parameters in the
Presence of Classification Errors
Reported values of statistical features for neuronal
clusters, like mean firing frequency or coefficient of
variation are often taken for granted. However, one
should be aware of deviations caused by clustering
errors. Figure 2 shows one example of a cluster
associated with a single neuron. It is obvious that
variations around the mean spike shape are large,
indicating a possible mixture of more spike shapes.
Figure 2: Example of bad classification (clustering) of
spikes.
2.3 Statistical Parameters
Statistical parameters are introduced to describe the
firing patterns of neurons, often observed through
the so called interspike interval histogram (ISIH).
This is a distribution of the observed time intervals
between successive spikes collected in bins of fixed
width.
Standard parameters are used to compare different
models. They are applied to describe individual
clusters. Mean corresponds to the average interspike
interval (ISI), whereas the median is the middle
value of a finite ordered list of these ISIs. Skewness
and kurtosis are also used, which are measurements
for the asymmetry and the peakiness of the ISIH
respectively (NIST, 2010). Coefficient of variation
C
V
and spiking randomness (Kostal et al., 2007)
are also included in the study. C
V
is the ratio of the
standard deviation divided by the mean, and
represents spiking variability. Spiking randomness is
a mathematical measure based on the entropy in the
signal. Roughly speaking, this entropy increases
with the larger variability of different ISIs and with
10 20 30 40 50 60
-0.01
0
0.01
sam
p
les
amplitude (V)
spike shape 1
spike shape 2
2
1
2
signal power
SNR=
noise power
*(std( ))
n
i
i
x
nnoise
=
=
∑
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
170
more freedom in the serial ordering of the ISIs in the
spike train (Kostal et al., 2007).
To detect bursting activity, some new parameters
are included as well (Gligorijevic et al., 2010).
Pause_index is the ratio of the number of ISIs
longer than 50 ms over the number of ISIs shorter
than 50 ms, whereas the pause_ratio is similarly
defined using instead the sum of these interval
lengths to calculate the ratio. Mod_burst is the ratio
of the number of ISIs less than 10 ms to the ISIs
longer than 10 ms. Finally, to quantify fast activity
yet formally not bursting, we define the
“Percentage window > 5 spikes” as the percentage
of fixed windows (here 100 ms is used) in which at
least 5 spikes appear.
2.4 Calculation of Errors
We can compare values and errors of specified
parameters at three different moments of the spike
train analysis based on the following three models:
• Continuous underlying distribution.
• Sampled distribution after taking values
conforming to the continuous distribution for
the interspike intervals (Figure 3a).
• Distribution after clustering (Figure 3b).
We extracted the described parameters from the
computed ISIHs. These parameters assist us in
describing the firing model of a neuron.
To compare the three different models, the errors
on used statistical features have to be calculated.
For example, the error between the mean of the
sampled distribution and the distribution after
clustering is calculated as in formula 2. The error
shows how this value deviates after clustering
compared to the one before. This deviation error
could therefore be larger than 100% in contrast to
the classification errors, which could potentially
reach up to 100% (when all the spikes are assigned
to the wrong cluster).
(%) *100
clustered sampled
sampled
mean mean
error
mean
−
=
(2)
The behaviour of the parameters is examined for
different distributions and different SNRs in the
sense of their robustness (to errors) and information
that they carry. Also, after clustering, some of the
spikes are not detected by the algorithm, which can
be observed as peaks on multiples of mean firing
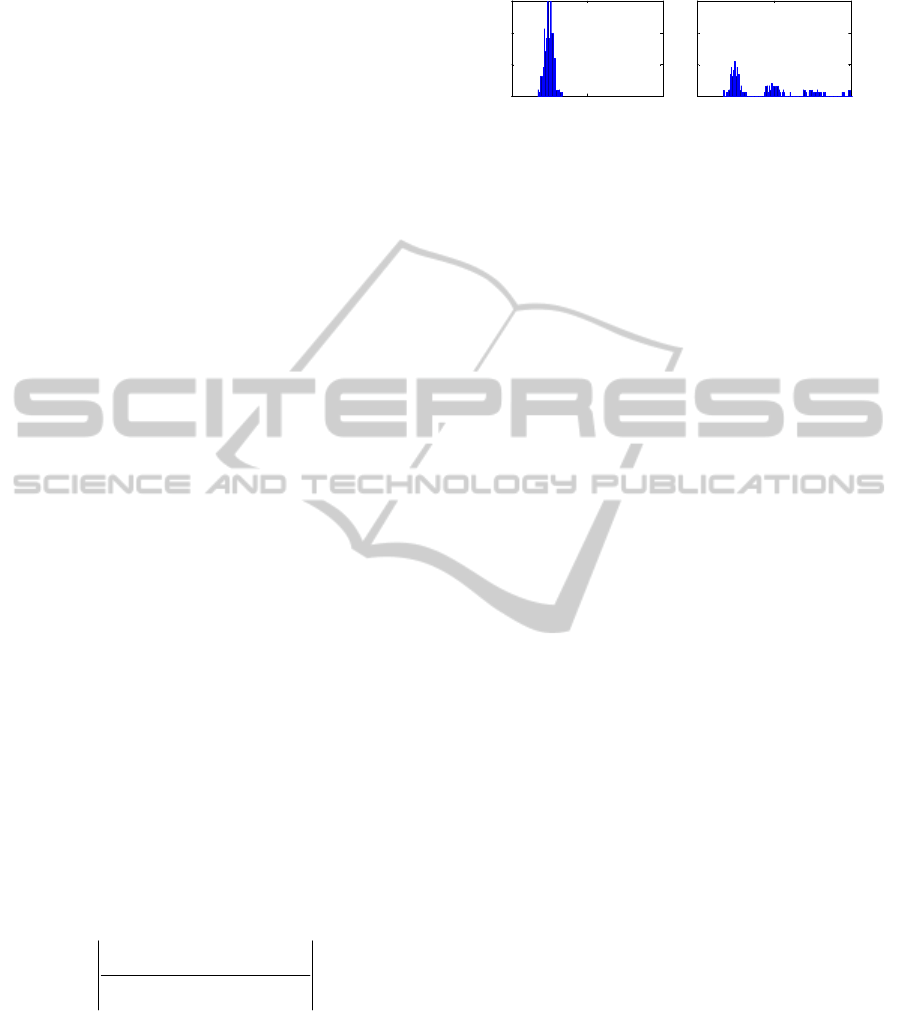
frequency (Figure 3b).
Figure 3: (a) Sampled normal distribution provides ISIs
for generation of the artificial neuronal signal. (b) ISIH
after clustering (using a spike sorting algorithm).
2.5 Overclustering
Sometimes the clustering outcome provides clusters
with similar shapes and it remains unknown if it is a
result of “overclustering” of a single neuron activity.
To investigate this case and its reflection on values
of parameters, the following approach was adopted.
Two distributions of interspike intervals can be
compared after splitting the underlying distribution.
More specific, a certain percentage of the total of
ISIs constructing the underlying distribution is
assigned to one cluster. The second cluster consists
of the remaining ISIs of the same underlying
distribution. It was investigated if these separate
clusters have similar enough values for certain
parameters. If so, this could indicate the need to
merge them.
3 RESULTS AND DISCUSSION
3.1 Parameter Estimation
The goal we set was to investigate statistical
parameters and their information capacity for ‘low’
quality clusters. More than 120 signals were
examined with different timestamp distributions,
different low SNRs and different spike shapes. The
median was found to be a better feature to
approximate the mean frequency of the underlying
distribution than the extracted mean of the
reconstructed distribution after clustering. Indeed,
the calculated errors between the values of the
median describing the two sampled models - before
and after clustering - are in all of our simulations
smaller compared to the errors of the mean. These
errors reduce when the SNR increases, so the
estimation of the mean firing frequency becomes
better. An example is shown in Figure 4 for signals
with different low SNRs.
C
V
parameter was found to be informative and
reasonably accurate (some examples in Table 1).
0 250 500
0
10
20
30
Length InterSpike Intervals (ms)
Number of intervals
original sampled ISI
0 250 500
0
10
20
30
ISI af ter clustering
RELIABILITY OF STATISTICAL FEATURES DESCRIBING NEURAL SPIKE TRAINS IN THE PRESENCE OF
CLASSIFICATION ERRORS
171
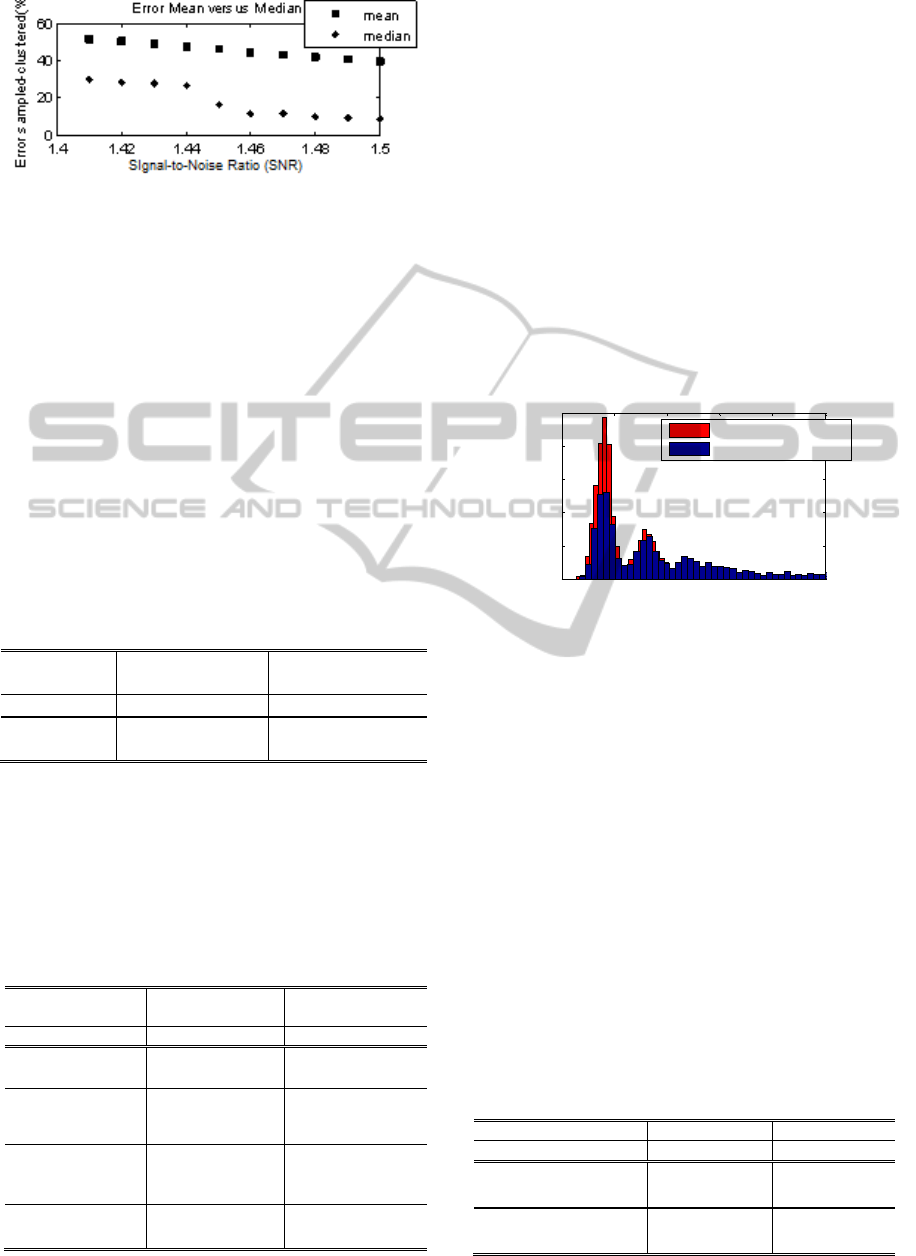
Figure 4: Error mean versus error median for signals with
different low SNRs.
C
V
>1 was reported as an indicator for bursting
activity (Kostal et al., 2007). In our simulations this
feature has higher values for signals with bursts,
approximating 1 or higher after clustering
substantiating this claim. As a consequence of low
SNR many spikes are not detected, hence the change
of the standard deviation and mean will lead to the
large deviations of the Cv. Nevertheless, it has
informative capacity indicating main features of
distribution (Table 1).
Table 1: Example of two normal distributions (with and
without bursts) corresponding to the two active neurons
recorded in one signal. C
V
is calculated for two models -
before and after clustering. The second column is a
repeated simulation with other values for the means of the
underlying distributions.
Mean (ms)
83,33
+bursts
125,00
75,00 +
bursts
133,33
Std (ms) 12,50 20,00 12,50 20,00
Cv,before_cl 0,60 0,17 0,45 0,15
Cv,after_cl 1,63 0,52 1,86 0,53
Spiking randomness indicates the variety of
spiking patterns. However, it showed large and
unpredictable errors, indicating little practical
usefulness. The mean error was 401,67 (±403,22) %.
Table 2: Examples of two normal timestamp distributions
(with and without bursts), selected for generating an
artificial signal. Bursting parameters are calculated for two
models - before (b_cl) and after clustering (a_cl).
Mean (ms)
100
+bursts
108,33
91,67 +
bursts
116,67
Std (ms) 12,50 20,00 12,50 20,00
Mod_burst, b_cl 0,31 0,00 0,22 0,00
Mod_burst, a_cl 0,29 0,02 0,22 0,02
Pause_index, b_cl 2,74 249,00 3,60
249,0
0
Pause_index_a_cl 2,22 13,93 2,57 10,79
Pause_ratio, b_cl 51,57 709,15 42,41
637,4
1
Pause_ratio, a_cl 27,04 79,18 21,88 55,57
Perc>5spikes, b_cl 3,96 0,00 3,30 0,00
Perc>5spikes, a_cl 3,30 0,00 2,82 0,00
Burst parameters can reveal the presence or
absence of bursts (Table 2). In this case both
features mod_burst and `percentage window > 5
spikes’ are larger than zero. On the other hand, the
values for pause_ratio and pause_index are smaller
than those values for signals without bursts. If all
these conditions are true, even modest bursting
activity of a neuron is always detected in our
simulations.
3.2 Overclustering
The mean and median proved to be significantly
different for the two clusters. Many missing
timestamps resulted in longer interspike intervals
(Figure 5), hence higher values for mean and median
compared to those of the underlying distribution.
Figure 5: Two overlaid ISIHs, originally assumed as
belonging to different clusters but having the same
underlying distribution; dominant peaks matching almost
perfectly.
Although not accurate in cases of individual
clusters, skewness and kurtosis proved to be good
indicators of overclustering. Values for the two
clusters are similar (example in Table 3), with
respectively differences of 15,61% and 18,98%. As
a comparison, these differences are at least twice as
large in cases of different distributions.
Fitting the ISIHs with analytical functions after
clustering could be another condition to decide if the
two clusters should be merged.
Table 3: To simulate overclustering, one original normal
distribution (orig_distr) is randomly split up into two
clusters. A certain percentage of timestamps is assigned to
the first cluster and the other timestamps to the second
cluster. Values for skewness and kurtosis are calculated
and compared. Two examples are given.
Mean (Std) (ms) 66,67 (12.5) 66.67 (12.5)
% cluster 1/ cluster 2 70 30 80 20
skewness, orig_distr 0.09 0.09
skewness, after_cl 2,17 1,81 2,24 2,02
kurtosis, orig_distr 3,19 3,19
kurtosis, after_cl 9,12 7,43 9,38 9,97
0 2000 4000 6000 8000 10000
0
50
100
150
200
250
samples
interspike interval histogram
ISIH 1 (60% of cluster)
ISIH 2 (40% of cluster)
BIOSIGNALS 2012 - International Conference on Bio-inspired Systems and Signal Processing
172

4 CONCLUSIONS
This research examined the possibility of reliable
information extraction from neural clusters of bad
quality. It showed that features like the mean firing
frequency and burst detection can still be
successfully extracted.
In the future, existing as well as newly derived
parameters could be tested, possibly circumventing
the problems of missed spikes and thus adding
robustness and increasing the usefulness of the
extracted spike trains.
These strategies could be implemented in the
future as a tool that would help include previously
discarded information coming from more distant
neurons or signals corrupted in other ways, thus
greatly increasing the possibilities for observation of
brain conditioning. Initial results showed the
potential for keeping the signals of lower quality
while providing the trustworthy analysis, indicating
the possibility of their future implementation.
ACKNOWLEDGEMENTS
We acknowledge financial support from: GOA
MaNet, PFV/10/002 (OPTEC), FWO projects
G.0341.07 (Data fusion), G.0427.10N (Integrated
EEG-fMRI), IUAP P6/04 (DYSCO); IMEC SLT
PhD Scholarship. IBBT Future Health.
REFERENCES
Chan, H.-L. e.a. (2010). Complex analysis of neuronal
spike trains of deep brain nuclei in patients with
Parkinson’s disease. Brain Research Bulletin, 81(6),
p.534-542.
Dayan, P. & Abbott, L. F. (2005). Theoretical
Neuroscience: Computational and Mathematical
Modeling of Neural Systems 1e ed., The MIT Press.
Gligorijevic, I. e.a. (2010). Statistical analysis of neural
spike trains for evaluation of functional differences in
brain activity. Proc. of the BIOSIGNAL 2010
Conference.
Kostal, L., Lansky, P. & Rospars, J.-P. (2007). Neuronal
coding and spiking randomness. The European
Journal of Neuroscience, 26(10), p.2693-2701
NIST/SEMATECH. (2010) e-Handbook of Statistical
Methods, Retreived from: http://www.itl.nist.gov/
div898/handbook/.
Quiroga, R. Q., Nadasdy, Z. & Ben-Shaul, Y. (2004).
Unsupervised spike detection and sorting with
wavelets and superparamagnetic clustering. Neural
Computation, 16(8), p.1661-1687.
Rutishauser, U. (2011). OSort - Ueli Rutishauser’s
homepage, Retrieved from : http://www.urut.ch/new/
serendipidity/index.php?/pages/osort.html
Rutishauser, U., Schuman, E. M. & Mamelak A. N.
(2006). Online detection and sorting of extracellularly
recorded action potentials in human medial temporal
lobe recordings, in vivo. Journal of Neuroscience
Methods, 154, p. 204–224.
RELIABILITY OF STATISTICAL FEATURES DESCRIBING NEURAL SPIKE TRAINS IN THE PRESENCE OF
CLASSIFICATION ERRORS
173
