
INVESTIGATING MARKOV LOGIC NETWORKS
FOR COLLECTIVE CLASSIFICATION
Robert Crane and Luke K. McDowell
Department of Computer Science, U.S. Naval Academy, Annapolis, MD, U.S.A.
Keywords:
Collective classification, Statistical relational learning, Markov logic networks.
Abstract:
Collective Classification (CC) is the process of simultaneously inferring the class labels of a set of inter-linked
nodes, such as the topic of publications in a citation graph. Recently, Markov Logic Networks (MLNs) have
attracted significant attention because of their ability to combine first order logic with probabilistic reasoning.
A few authors have used this ability of MLNs in order to perform CC over linked data, but the relative ad-
vantages of MLNs vs. other CC techniques remains unknown. In response, this paper compares a wide range
of MLN learning and inference algorithms to the best previously studied CC algorithms. We find that MLN
accuracy is highly dependent on the type of learning and the input rules that are used, which is not unusual
given MLNs’ flexibility. More surprisingly, we find that even the best MLN performance generally lags that
of the best previously studied CC algorithms. However, MLNs do excel on the one dataset that exhibited the
most complex linking patterns. Ultimately, we find that MLNs may be worthwhile for CC tasks involving data
with complex relationships, but that MLN learning for such data remains a challenge.
1 INTRODUCTION
Classification is the task of assigning appropriate la-
bels to instances (or nodes). For instance, a simple
binary classification task could involve deciding if a
web-page is “spam” or not. Traditional classification
assumes that the nodes to be classified are indepen-
dent of each other. Often, however, there are rich re-
lational (or linked) dependencies between the nodes
(such as hyperlinks or social connections). By ex-
ploiting such links, techniques for collective classi-
fication (CC) (Chakrabarti et al., 1998; Neville and
Jensen, 2000) such as ICA and Gibbs sampling been
shown to substantially improve accuracy compared to
independent classification (Neville and Jensen, 2007;
Sen et al., 2008; McDowell et al., 2009).
Markov Logic Networks (MLNs) are a re-
cently developed, powerful formalism for learning
and reasoning about data with complex dependen-
cies (Richardson and Domingos, 2006). In particu-
lar, MLNs pair first order logic statements with a nu-
merical weight. With properly learned weights, infer-
ence may then be used to estimate desired probabili-
ties (such as the most likely class label) from the given
evidence. Because of their expressive power and so-
phisticated learning and inference algorithms, MLNs
have attracted significant attention and been applied
to a wide range of problems (Richardson and Domin-
gos, 2006; Singla and Domingos, 2005; Riedel and
Meza-Ruiz, 2008; Chechetka et al., 2010; Mihalkova
et al., 2011).
The ability of MLNs to express complex rules
about interrelated objects, with learned weights that
express the strength of each rule, makes them a natu-
ral candidate for CC tasks. In addition, the existence
of multiple inference algorithms, with a freely avail-
able and tuned implementation (Kok et al., 2006),
offers the promise of obtaining strong results for
CC with (hopefully) minimal effort. Indeed, a few
authors have already considered applying MLNs to
this task (Lowd and Domingos, 2007; Huynh and
Mooney, 2009). However, as we describe in Sec-
tion 2.3, this prior work has not established whether
MLNs can actually yield better results for CC than
competing techniques.
This paper makes three primary contributions.
First, we provide the first evaluation of the most
prominent MLN learning and inference techniques
when applied to CC for a wide range of synthetic and
real data. In particular, we evaluate data with varying
amounts of autocorrelation (Jensen et al., 2004), use-
ful attributes, and known labels, enabling us to draw
broader conclusions. Overall, we find that the popular
MCSAT algorithm performs well, but, surprisingly,
5
Crane R. and K. McDowell L..
INVESTIGATING MARKOV LOGIC NETWORKS FOR COLLECTIVE CLASSIFICATION.
DOI: 10.5220/0003702600050015
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 5-15
ISBN: 978-989-8425-95-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

the simpler MCMC algorithm often performs better,
even in the presence of the kinds of near-deterministic
dependencies that MCSAT’s modifications to MCMC
were specifically designed to address. Second, we
provide the first systematic comparison, for CC, of
the best MLN techniques vs. non-MLN techniques.
Given their flexibility and sophistication, we expected
MLNs to deliver very strong results. We find, how-
ever, that while MLNs can outperform simple CC al-
gorithms such as ICA, they generally lag behind the
performance of the best CC algorithms such as ICA
C
and Gibbs sampling. Nonetheless, we identify one
situation in which MLNs outperform the other al-
gorithms, and discuss how this may result from the
more complex linking relationships in that dataset.
Finally, we identify and measure the impact of four
algorithmic/modeling factors that significantly affect
MLN behavior. Most of the factors are not surprising
by themselves, but we show how MLN accuracy can
be very sensitive to some of them, in dataset-specific
ways. Such information should be useful to future re-
searchers seeking to use MLNs for CC or other tasks.
The next section describes background on CC,
MLNs, and related work. Sections 3 and 4 present our
experimental methods and results. Finally, Section 5
concludes.
2 BACKGROUND
Below we summarize collective classification (CC),
MLNs, and other related work.
2.1 Collective Classification
Consider the task of predicting whether a web page
belongs to a professor or a student. Conventional ap-
proaches ignore the links and classify each page us-
ing attributes derived from its content (e.g., words
present in the page). In contrast, a technique for re-
lational classification explicitly uses the links to con-
struct additional features for classification (e.g., for
each page, include as features the words from hyper-
linked pages). Alternatively, even greater (and usu-
ally more reliable) increases can occur when the class
labels of the linked pages are used to derive rele-
vant relational features (Jensen et al., 2004). How-
ever, using features based on these labels is chal-
lenging because some or all of these labels are ini-
tially unknown. Thus, their labels must first be pre-
dicted (without using relational features) and then re-
predicted in some manner (using all features). This
process of jointly inferring the labels of interrelated
nodes is known as collective classification (CC). A
number of algorithms have been proposed for CC in-
cluding relaxation labeling, the Iterative Convergence
Algorithm (ICA), belief propagation, and Gibbs sam-
pling (see (Sen et al., 2008) for a summary).
2.2 Markov Logic Networks
A Markov Logic Network (MLN) is a set of first-order
formulas and their associated weights (Richardson
and Domingos, 2006). Each formula represents some
kind of relational rule, but, unlike in pure first-order
logic, a rule may be violated without causing unsat-
isfiability of the entire system. Instead, the weight
associated with each formula specifies how unlikely
a world is in which that formula is violated. Thus,
weights determine the importance of the correspond-
ing formulas during inference.
Weights are typically attached to the rules by su-
pervised learning. These weights can be learned
generatively, based on pseudo-likelihood (Richard-
son and Domingos, 2006), or discriminatively, us-
ing algorithms like voted perceptron (VP) (Singla
and Domingos, 2005), conjugate gradient (specifi-
cally, PSCG (Lowd and Domingos, 2007)), or diag-
onal Newton (DN) (Lowd and Domingos, 2007).
Given a set of rules with attached weights, and a
set of evidence literals (such as the attributes of a node
and possibly some known labels), approximate MLN
inference can be used to infer either the most likely as-
signment of truth values to all unknown literals (MAP
inference) or to compute the conditional probabilities
for the values of each unknown literal. Inference of
the former type can be performed with techniques
like MaxWalkSAT (cf, (Richardson and Domingos,
2006)). In this paper, we include MAP-based re-
sults with MaxWalkSat for completeness, but focus
on the latter case of computing conditional probabil-
ities. The first algorithm used for this type of MLN
inference was Gibbs sampling (MCMC) (Richardson
and Domingos, 2006), but it has great difficulty in the
presence of near-deterministic dependencies. Subse-
quently, (Poon and Domingos, 2006) introduced MC-
SAT, which alleviates these problems of MCMC. Be-
lief propagation (BP) can also be used (Richardson
and Domingos, 2006; Chechetka et al., 2010).
2.3 Related Work
MLNs have been used or proposed for a wide range
of tasks. For instance, (Richardson and Domingos,
2006) describe link prediction, link-based clustering,
social network modeling, and object identification in
an MLN framework. (Riedel and Meza-Ruiz, 2008)
ICAART 2012 - International Conference on Agents and Artificial Intelligence
6

Table 1: Summary of related work that has evaluated MLNs for object-based collective classification. The second and third
columns summarize the learning and inference algorithms that were evaluated with MLNs; see Section 2.2 for references and
explanation of acronyms. Algorithms shown in curly braces were considered but not reported on. The fourth column lists the
baseline algorithms (i.e., those not based on MLNs) that were also evaluated, if any. The last column lists the datasets that
were used with CC (excluding datasets used for other tasks).
Learning Algs. Inference Algs. Inference Algs. Datasets used
(for MLNs) (for MLNs) (non-MLNs) for CC
(Lowd and Domin-
gos, 2007)
VP, CD, DN, PSCG MCSAT None WebKB
(Huynh and
Mooney, 2009)
PSCG,
Max Margin-based
MCSAT, LPRelax,
MaxWalkSAT
None WebKB
(Dhurandhar and
Dobra, 2010)
PSCG,
{generative}
MCMC,
{MaxWalkSAT}
Gibbs, DRN Cora, IMDb, UW-CSE,
synthetic
(Chechetka et al.,
2010)
PSCG Belief propagation
(BP)
Max-margin graph
cuts
Three video-image spa
collections
This paper VP, DN, PSCG, spa
generative
MCSAT, MCMC, s
BP, MaxWalkSAT
Gibbs, ICA, ICA
C
,
wvRN, MRW
Cora, CiteSeer, spacer
WebKB, synthetic
use MLNs for natural language processing, taking ad-
vantage of relational aspects of semantics.
Some of these applications of MLNs involve
reasoning that can be considered collective in na-
ture, such as collective entity resolution (Singla and
Domingos, 2005; Lowd and Domingos, 2007), col-
lective semantic role labeling (Riedel and Meza-Ruiz,
2008), and collaboration prediction (Mihalkova et al.,
2011). These publications have demonstrated that
MLNs can reason with a wide variety of information
and handle complex dependencies.
For this paper, the most relevant other work with
MLNs concerns applications where collective reason-
ing is specifically applied for predicting the class la-
bels of inter-linked objects (e.g., collective classifica-
tion), as opposed to being used for entity resolution or
collective role labeling. We are aware of only four pa-
pers that directly address this “object-based” CC with
MLNs. Table 1 summarizes these investigations; be-
low, we discuss each in turn.
(Lowd and Domingos, 2007) and (Huynh and
Mooney, 2009) both focused on improving discrim-
inative learning for MLNs. In particular, both pa-
pers proposed one or more new techniques for MLN
weight learning, then evaluated the new algorithms on
object-based CC and one other inference task (entity
resolution or bibliographic segmentation). For CC,
they evaluated only one dataset (WebKB, which we
also use). Moreover, they both focus on improving
learning for MLNs in particular, and thus they do not
compare against any techniques that are not based on
MLNs. Thus, they demonstrate that MLNs can per-
form CC, but do not demonstrate that MLNs are par-
ticularly well-suited for this task.
(Chechetka et al., 2010) utilize MLNs to collec-
tively classify entities identified in images. Relational
information is defined as attributes shared commonly
between entities in different pictures. They evalu-
ated three different image datasets, but used only a
single type of learning and inference (PSCG and be-
lief propagation, respectively). They did compare
against one non-MLN based technique, a graph-cut-
based approach. However, this approach did not use
the same set of features as the MLN, hampering our
ability to directly evaluate the performance advantage
of the MLN itself. In addition, they did not com-
pare against well-known techniques for CC like ICA
or Gibbs sampling.
The only work of which we are aware that di-
rectly compares MLNs with a traditional CC algo-
rithm is the draft manuscript of (Dhurandhar and
Dobra, 2010). In particular, they compared MLNs
against a relational dependency network (RDN) with
Gibbs, as we do in this paper. They evaluate perfor-
mance on some synthetic data and on Cora, IMDb,
and UW-CSE, three well-known real datasets. They
found that the RDN (with Gibbs sampling) and the
MLN performed very similarly. Their goal, how-
ever, was to evaluate when CC outperforms non-
collective classification, not primarily to evaluate how
well MLNs compare to other CC approaches. Con-
sequently, their results leave many unanswered ques-
tions regarding the relative performance of MLNs.
First, while the authors claim that the MLN results
were “qualitatively the same” regardless of whether
generative learning or discriminative learning was
used, and regardless of whether MCMC or MaxWalk-
SAT was used for inference, results are given only
for MCMC with discriminative learning. Our results,
however, suggest that the choice of learning and in-
ference algorithm can have a significant impact, with
MaxWalkSAT performing especially poorly for CC.
INVESTIGATING MARKOV LOGIC NETWORKS FOR COLLECTIVE CLASSIFICATION
7

Second, even for the one MLN algorithm for which
results are reported, they vary only one aspect of the
real datasets (the “labeled fraction”, see Section 3),
leaving only a small number of accuracy results for
the real data from which to generalize. Third, their pa-
per considers only one collective inference algorithm
that is not based on MLNs (Gibbs sampling with
RDNs), preventing direct comparison with other im-
portant CC algorithms such as ICA or the relational-
only algorithms wvRN and MRW that we describe
later.
1
Finally, their paper does not describe the actual
MLN rules that were used for the experiments, which
prevents replication.
2
In our experience, the details of
these rules sometimes lead to dramatic differences in
performance. Thus, their paper is a relevant point of
comparison regarding the use of MLNs, but does not
establish the relative performance of MLNs vs. com-
peting techniques for CC.
3 METHODS
3.1 Data Generation
We used the following standard data sets (see Ta-
ble 2):
• Cora (see (Sen et al., 2008)): A collection of
machine learning papers categorized into seven
classes.
• CiteSeer (see (Sen et al., 2008)): A collection of
research papers drawn from the CiteSeer collec-
tion.
• WebKB (see (Neville and Jensen, 2007)): A col-
lection of web pages from four computer science
departments.
• Synthetic: We generate synthetic data using the
graph generator of (Sen et al., 2008) . Similar to
their defaults, we use a link density of 0.2. A key
parameter is the degree of homophily (dh), which
indicates how likely a node is to link to another
node with the same label. Similar to Sen et al., we
use a default of dh = 0.7 but also consider higher
and lower values.
The real datasets are all textual. For these datasets,
each non-relational feature (attribute) represents the
1
They do evaluate one relational-only algorithm, DRN,
but this is not a collective algorithm.
2
In a private communication, the first author of (Dhu-
randhar and Dobra, 2010) stated that creating MLN files
that worked well on the datasets had been very challenging,
but that he no longer had access to the files and thus could
not describe them.
Table 2: Data sets summary.
Characteristics Cora CiteSeer WebKB Syn.
Total nodes 2708 3312 1541 n.a.
Avg. # nodes per test set 400 400 385 250
Avg. links per node 2.7 2.7 6 1.7
Class labels 7 6 6 5
Non-rel. features avail. 1433 3703 100 10
Non-rel. features used 10–100 10–100 10–100 10
Number of folds 5 5 4 10
presence or absence of a word in the corresponding
document. Our version of WebKB has 100 words
available. For Cora and CiteSeer, we used infor-
mation gain to select the 100 highest-scoring words,
based on (McDowell et al., 2007), which reported that
using more did not improve performance. To simu-
late situations where more or less non-relational in-
formation is available, we vary the actual number of
attributes used from 10 to 100 (choosing randomly
from the available 100).
For the synthetic data, ten binary attributes are
generated using the technique described by (McDow-
ell et al., 2009). This model has a parameter ap (at-
tribute predictiveness) that ranges from 0.0 to 1.0; it
indicates how strongly predictive the attributes are of
the class label. We evaluate ap using the values 0.2,
0.4, 0.6, and 0.8.
Each dataset has links between the nodes. We
evaluate two variants of WebKB: one using the regu-
lar links (WebKB-direct) and one using only the “co-
citation” links (WebKB-co). A “co-link” exists be-
tween two nodes when some other node links to both
of them; prior work has found these links to be more
informative than regular links for WebKB.
In many real-world test graphs, there is some frac-
tion of the nodes whose labels are already known, and
these labels can significantly assist the inference pro-
cess. We call this the “labeled proportion” (l p) of the
graph, and randomly select 0%, 10%, or 50% of the
nodes in each test set to be known. We focus par-
ticularly on the lp = 10% case, which is a “sparsely
labeled task” that is common in real data (Gallagher
et al., 2008).
3.2 MLN Comparison
MLN experiments utilized the Alchemy toolkit (Kok
et al., 2006). We report results using both discrimi-
native learning (using diagonal Newton) and genera-
tive learning (using pseudo-likelihood), using default
settings. For discriminative learning, the class label
predicate was specified as non-evidence. For genera-
tive learning, no non-evidence predicates were used.
We performed inference, using the default set-
tings, with four prominent algorithms available in
ICAART 2012 - International Conference on Agents and Artificial Intelligence
8

Alchemy: belief propagation (BP), Markov chain
Monte Carlo (MCMC), MCSAT, and MaxWalkSAT
(“MAP”) (see Section 2.2). Note that MAP seeks the
most likely assignment of labels for the entire graph,
rather than the most likely assignment for each node.
It is thus unsurprising that we find that it it fares
poorly when we measure per-node accuracy in Sec-
tion 4. We include it for completeness and because
(Huynh and Mooney, 2009) find that this type of in-
ference can still yield good accuracy in some cases.
Our inclusion of the other three algorithms was based
on prior work (see Table 1).
For each attribute j we created a MLN rule like
attr_j(o, +v) => class(o, +c)
which relates the value v of the jth attribute for object
o and the class label c of that object. The plus signs
cause Alchemy to learn a different weight for every
sensible combination of the values of v and c.
To perform CC, we also need a rule like
class(o1,+c1) ˆ LinkTo(o1,o2) => class(o2,+c2)
which relates the class labels of objects o1 and o2 if
they are linked to each other. The precise choice of
relational rule to use here is challenging; Section 4.2
describes specifically which rules were used and ex-
amines the impact of our choices.
3.3 Baseline Algorithms
We compare MLNs against two CC algorithms that
were previously found (McDowell et al., 2009) to
have the most reliable performance, Cautious ICA
(ICA
C
) (Neville and Jensen, 2000) and Gibbs sam-
pling (Jensen et al., 2004), and also against a sim-
pler CC algorithm that has been frequently studied,
ICA (Sen et al., 2008). These three algorithms use
both attributes and relational features. They employ a
naive Bayes classifier with “multiset” relational fea-
tures as the local classifier, a combination that was
previously found to yield very strong results (Mc-
Dowell et al., 2009). Note that the baseline “Gibbs” is
essentially the same as “MCMC” used for the MLNs,
except that MCMC uses the MLN model to produce
label predictions instead of the naive Bayes classifier
used by Gibbs.
For perspective on the accuracy results, we also
evaluate three simple baselines. AO (attribute-only) is
the naive Bayes classifier described above, but where
only the attribute information is used. We also con-
sider two relational-only classifiers: wvRN (Mac-
skassy and Provost, 2007) and MRW (Lin and Cohen,
2010). wvRN is a standard baseline for evaluating
CC that repeatedly computes label estimates based
on the labels of all linked neighbors. MRW is a re-
cently proposed algorithm that estimates labels based
on repeated random graph walks starting from labeled
nodes. Both algorithms may perform very well if a
graph exhibits high homophily and has a large enough
value of lp.
3.4 Test Procedure
We conducted an n-fold cross-validation study for
each tested algorithm, and report the average classi-
fication accuracy across the test sets. For WebKB, we
treated each of the four schools as a separate fold. For
Cora and CiteSeer, we created five disjoint test sets
by using “similarity-driven snowball sampling” (Mc-
Dowell et al., 2009). For all 3 real datasets we tested
on one graph and trained on the union of the others.
For the synthetic data, we performed 10 separate
trials. For each trial we generated three graphs and
used two for training and one for testing.
4 RESULTS
This section describes our experimental results. Con-
figuring the MLNs to obtain results that were compet-
itive with the non-MLN baselines turned out to sur-
prisingly difficult. For simplicity, Section 4.1 first
describes our primary results which compare well-
configured MLNs against each other and against the
non-MLN baselines. Next, Section 4.2 discusses the
specific MLN configurations that were used and the
lessons we learned that were necessary to obtain good
accuracy with MLNs.
4.1 Primary Evaluation on MLNs
Table 3 shows accuracy results for the various datasets
for the case where l p = 10% (see Section 3.1). For
instance, Table 3 (part A) shows that MCSAT with
discriminative learning (i.e., MCSAT-d) achieved an
accuracy of 76.6% for Cora when using 50 attributes,
and an accuracy of 70.1% when averaged over trials
with 10, 20, 50, and 100 attributes. Below we high-
light some key results from this table. We first eval-
uate the relative performance of the MLN algorithms
to each other, and then compare to other algorithms.
Result 1: Discriminatively Learned MLNs Gener-
ally Outperformed Generatively Learned MLNs.
When comparing the best discriminative results vs.
the best generative results, discriminative learning al-
most always was best, ranging from a gain of about
1% for Citeseer to a gain of about 14% for WebKB-
co. In contrast, (Dhurandhar and Dobra, 2010) re-
port that, for the datasets they considered, accuracies
were “qualitatively the same” for both types of learn-
ing. We find instead that prior work (e.g., (Singla
INVESTIGATING MARKOV LOGIC NETWORKS FOR COLLECTIVE CLASSIFICATION
9
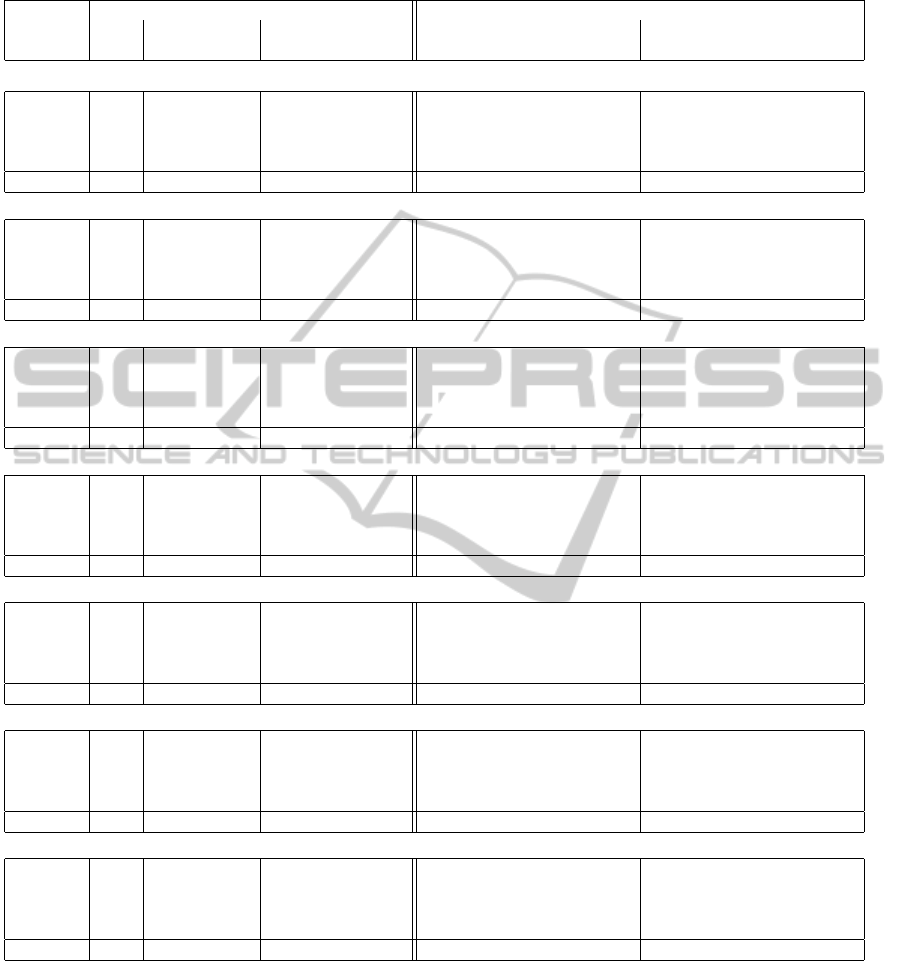
Table 3: Accuracy results with the “labeled fraction” (l p)=10%. “dh” is the degree of homophily in the data. Values shown
in bold are the maximum for that row for either the left side (non-MLNs) or right side (MLNs) of the table.
Baseline Algorithms (non-MLN) MLNs
Attrs. Relat. only Attrs. + Relat. Discriminative learning Generative learning
only wvRN MRW ICA ICA
C
Gibbs BP MCSAT MCMC MAP BP MCSAT MCMC MAP
lww lww lww lww ww ww ww ww ww ww ww ww ww ww ww
A.) Cora
10 attrs. 42.7 64.2 66.1 48.5 63.8 60.6 46.8 57.8 52.2 33.5 50.9 57.6 49.9 41.4
20 attrs. 51.4 64.2 66.6 61.0 71.9 72.7 68.2 66.4 69.5 48.3 60.4 62.5 60.3 45.5
50 attrs. 63.4 64.2 66.4 74.7 77.9 78.2 75.4 76.6 75.1 64.6 71.7 69.3 71.8 56.3
100 attrs. 73.5 64.2 66.2 81.0 80.2 80.4 78.6 79.8 78.8 69.9 77.5 73.7 77.3 66.8
Average 57.7 64.2 66.4 66.3 73.5 73.0 67.3 70.1 68.9 54.1 65.1 65.8 64.8 52.5
B.) Citeseer
10 attrs. 34.4 65.0 62.7 39.0 62.4 56.5 57.1 59.5 53.4 40.4 48.1 56.9 49.4 37.5
20 attrs. 44.6 65.0 63.1 50.5 66.1 64.9 62.4 61.7 59.5 49.5 55.1 62.9 56.6 47.8
50 attrs. 60.9 65.0 62.8 68.1 71.8 71.4 68.6 69.8 68.6 60.5 66.2 67.2 66.4 57.2
100 attrs. 70.6 65.0 62.5 74.4 75.1 74.7 73.3 74.2 73.5 69.0 73.3 73.7 73.4 64.1
Average 52.6 65.0 62.8 58.0 68.9 66.9 65.4 66.3 63.7 54.9 60.7 65.2 61.4 51.6
C.) WebKB-direct (direct links only)
10 attrs. 42.9 38.5 48.3 43.1 53.4 38.9 53.6 49.0 55.5 22.5 41.0 39.5 41.5 25.0
20 attrs. 47.1 38.5 48.1 47.4 51.9 53.0 56.7 53.6 57.7 27.0 53.3 42.5 54.7 25.8
50 attrs. 52.1 38.5 48.6 55.2 58.7 52.9 62.9 63.0 63.9 25.9 58.6 45.6 59.8 27.2
100 attrs. 55.3 38.5 48.3 57.9 61.4 57.4 57.3 67.7 68.0 23.8 62.1 44.4 63.5 27.8
Average 49.3 38.5 48.3 50.9 56.4 50.6 57.6 58.3 61.3 24.8 53.7 43.0 54.8 26.4
D.) WebKB-co (co-citation links only)
10 attrs. 42.9 47.0 69.7 40.6 60.3 28.0 40.3 48.4 55.7 53.7 29.8 39.0 29.6 43.8
20 attrs. 47.1 47.0 69.1 56.2 64.9 29.1 41.4 34.5 56.4 54.5 31.3 40.0 38.8 43.3
50 attrs. 52.1 47.0 67.9 60.7 71.5 28.8 56.9 62.5 62.4 61.5 35.9 45.5 54.3 45.9
100 attrs. 55.3 47.0 68.6 52.2 74.6 29.3 42.2 61.3 57.6 38.0 38.3 42.7 55.7 60.5
Average 49.3 47.0 68.8 52.4 67.8 28.8 45.2 51.7 58.0 51.9 33.8 41.8 44.6 48.4
E.) Synthetic (dh = 0.5)
ap = 0.2 36.4 39.1 43.1 38.2 47.2 48.3 45.7 49.6 46.5 37.8 44.4 48.1 45.5 40.1
ap = 0.4 48.6 39.1 43.0 53.1 62.7 62.3 59.2 62.9 59.7 50.7 56.9 58.3 58.7 50.1
ap = 0.6 61.2 39.1 43.2 67.2 71.1 72.0 70.0 71.5 70.7 58.7 69.6 68.5 70.7 58.6
ap = 0.8 72.7 39.1 42.6 78.9 80.5 81.3 80.7 79.7 80.8 65.9 80.1 77.2 80.6 65.1
Average 54.8 39.1 43.0 59.4 65.4 66.0 63.9 65.9 64.4 53.3 62.8 63.0 63.9 53.5
F.) Synthetic (dh = 0.7)
ap = 0.2 35.7 58.4 59.9 43.7 62.9 62.2 44.7 49.6 43.6 37.3 51.4 51.3 51.7 45.7
ap = 0.4 48.7 58.4 59.9 61.1 71.3 76.1 67.8 60.9 67.7 49.2 66.5 63.3 68.1 56.6
ap = 0.6 61.6 58.4 59.5 76.1 82.5 83.4 81.5 73.4 82.6 60.8 78.4 68.0 78.9 65.6
ap = 0.8 72.9 58.4 59.9 85.0 88.1 88.3 87.3 78.4 87.8 71.4 86.4 73.0 86.6 71.2
Average 54.7 58.4 59.8 66.5 76.2 77.5 70.3 65.6 70.4 54.7 70.7 63.9 71.3 59.7
G.) Synthetic (dh = 0.9)
ap = 0.2 37.0 80.5 83.3 48.2 76.3 79.1 41.4 35.2 36.3 37.5 67.7 49.9 65.6 53.4
ap = 0.4 50.0 80.5 84.0 66.4 86.7 88.9 53.2 39.5 44.8 44.0 83.4 51.1 81.5 63.6
ap = 0.6 62.7 80.5 83.9 82.4 91.9 92.9 71.0 47.2 66.4 56.9 91.2 59.6 90.4 70.9
ap = 0.8 73.6 80.5 84.0 91.8 95.1 95.1 93.2 70.4 94.2 76.7 95.5 64.1 95.9 79.0
Average 55.8 80.5 83.8 72.2 87.5 89.0 64.7 48.1 60.4 53.8 84.4 56.1 83.3 66.7
and Domingos, 2005; Lowd and Domingos, 2007;
Huynh and Mooney, 2009)) was correct to focus ex-
clusively on discriminative learning, at least for CC,
since it generally has better performance. In some
cases, however, we found that generative learning was
superior. For instance, for the synthetic data where
the degree of homophily is very high (Table 3 part
G), the discriminative learner appears to have great
difficulty learning appropriate weights. In particular,
with discriminative learning, performance for every
inference algorithm decreases as dh increases from
0.7 to 0.9 (e.g., from 65.6% to 48.1% for MCSAT-
d). This is the opposite of the expected trend and
the trend demonstrated by the baseline algorithms and
most of the generative MLN results. This exception
to the general rule suggests that more work may be
needed to improve discriminative learning in the pres-
ence of very strong correlations, even when an algo-
ICAART 2012 - International Conference on Agents and Artificial Intelligence
10

rithm like MCSAT, which is supposed to deal well
with such correlations, is used for inference.
Result 2: The Best MLN Performance was Almost
Always Achieved by MCSAT or MCMC. Of the
seven datasets shown in Table 3, MCMC and MCSAT
each had the best average performance of the MLNs
in three cases. In the one remaining case (the pre-
viously mentioned synthetic data where dh = 0.9),
BP with generative learning (BP-g) performs best,
closely followed by MCMC-g, but MCSAT-d and
MCSAT-g both perform very poorly (e.g., at best
56.1% for MCSAT vs. 83.3 % for MCMC-g). This
poor behavior of MCSAT is surprising, since MCSAT
was specifically designed to modify MCMC so that it
better handled near-deterministic dependencies (Poon
and Domingos, 2006), as represented by the high ho-
mophily here. MCSAT has generally been presumed
to be the superior inference algorithm, and is the
default algorithm used by Alchemy. However, Ta-
ble 1 shows that no other work has actually compared
MCMC and MCSAT for CC. Our results show that
both algorithms should be considered, and more work
is needed to better determine when each algorithm is
likely to be superior to the other.
Result 3: MLNs can Perform Effective Collec-
tive Classification, Consistently Outperforming
Attribute-only or Relational-only Baselines. For
instance, Table 3 shows that the best MLN algo-
rithm always outperformed attribute-only classifica-
tion (AO). In addition, the best MLN algorithm gen-
erally outperformed the best relational-only algorithm
(MRW), provided that a reasonable number of at-
tributes (at least 20) were available. For instance,
MRW achieved an accuracy of only 66.4% on Cora
compared to an average of 76.6% with MCSAT-d.
This performance advantage of the MLNs is precisely
what we would hope for, since the MLNs use sophis-
ticated inference and more information than either
the relational-only or attribute-only baselines. How-
ever, actual results demonstrating that MLNs could
perform effective CC, yielding better accuracies than
such baselines, has not previously been reported (Sec-
tion 2.3 describes the one limited exception). More-
over, actually achieving these sensible results for
MLNs was non-trivial, as discussed in Section 4.2.
Result 4: The Best MLN Results Exceeded the Ac-
curacy of Simple Non-MLN CC Algorithms, but
Lagged that of the Best Non-MLN CC Algorithms.
We focus here, and in the remainder of the paper, on
four representative datasets (Cora, synthetic data with
dh = 0.7, WebKB-direct, and WebKB-co) and on the
best MLN algorithms (MCSAT-d and MCMC-d). Ta-
ble 3 shows that the accuracy of the best MLN al-
gorithm is almost always less than or equal to that
of ICA
C
(which has very strong overall performance)
but greater than the accuracy of the simpler, less ro-
bust ICA. For instance, with 20 attributes on Cora,
MCMC-d had an accuracy of 69.5%, compared to
71.9% for ICA
C
and 61.0% for ICA. The trend also
holds for Citeseer and for the synthetic data, even with
very high homophily (Table 3 part G), provided that
generative training is used as previously discussed for
this case. For all these cases, the magnitude of these
differences generally decreases as the number of at-
tributes or attribute strength increases, as would be
expected (McDowell et al., 2009).
However, the results with WebKB-direct provide
one interesting exception to this trend. Here MCMC
beats ICA
C
by 2-7% and BP and MCSAT also outper-
form ICA
C
on average. These results are likely due to
the more complex linking patterns of this dataset. For
instance, nodes labeled “Professor” tend to link di-
rectly to nodes labeled “Student” rather than to other
nodes labeled “Professor” (which is the pattern that
would be created by simpler “homophilic” linking as
present in datasets like Cora and Citeseer). However,
the co-citation links of WebKB have much higher
homophily (dh = roughly 0.88). Thus, the results
for WebKB-co in Table 3 show relative MLN perfor-
mance much more like Cora and Citeseer than like
WebKB-direct, although some of the algorithms have
more erratic overall behavior.
Table 4 summarizes the results of Table 3, focus-
ing on a comparison between the best MLN algo-
rithms vs. two representative non-MLN algorithms
(ICA and ICA
C
). We examine results pooled over
all of the real datasets and for the synthetic data with
dh = 0.7. We also consider results pooled over all real
datasets except WebKB-direct due to its more anoma-
lous behavior. To establish significance, we use one-
tailed paired t-tests accepted at the 95% confidence
level, appropriate because all of the test sets consid-
ered are disjoint. In many cases the performance dif-
ferences are significant and consistent with Result 4
as stated above. For instance, on the synthetic data
with ap = 0.2, MCSAT-d significantly outperforms
ICA by 5.9% but significantly underperforms ICA
C
by 13.2%.
Sensitivity of Results: Other experiments showed
that the four results discussed above for l p = 10%
generally hold for lp = 0% or l p = 50% as well.
In particular, the performance of the best MLN al-
gorithms remains between that of ICA
C
and ICA,
and discriminatively-trained MCSAT and MCMC are
generally the best MLN algorithms. Details can be
found in (Crane and McDowell, 2011), a preliminary
version of this work.
We also considered whether the MLNs needed
INVESTIGATING MARKOV LOGIC NETWORKS FOR COLLECTIVE CLASSIFICATION
11

Table 4: Performance comparison of MCSAT-d and MCMC-d against a simple CC algorithm (ICA) and a better CC algorithm
(ICA
C
). A positive number indicates an average accuracy win by the MLN algorithm, while a negative number indicates that
the non-MLN algorithm was better. Values in bold indicate statistically significant differences. The three column groupings
are: results pooled over all real datasets, results pooled over all real datasets except WebKB-direct, and results with synthetic
data. The individual column labels indicate the number of attributes used or the attribute predictiveness (ap), as appropriate.
All real data Real minus WebKB-direct Synthetic (dh = 0.7)
10 20 50 100 10 20 50 100 0.2 0.4 0.6 0.8
MCSAT-d vs. ICA 11.4 -1.2 -3.1 -3.8 12.9 -0.3 -1.8 -2.1 -5.9 -0.2 -2.7 -6.6
MCMC-d vs. ICA 11.1 -7.2 -2.5 -2.5 10.8 -6.3 -0.8 -0.4 -0.1 -6.6 -6.5 -2.8
MCSAT-d vs. ICA
C
-6.1 -9.1 -2.0 -1.9 -6.6 -12.2 -3.8 -4.3 -13.2 -10.4 -9.1 -9.7
MCMC-d vs. ICA
C
-6.3 -3.1 -2.6 -3.2 -8.7 -5.6 -4.8 -6.0 -19.2 -3.6 -0.1 -0.3
lww lww lww lww lww ww ww ww ww ww ww ww ww ww
more training data to perform well. Results (not
shown) on the synthetic data showed that quadrupling
the size of the training data usually boosted generative
accuracy by 0-2%, but actually harmed discriminative
accuracy. Thus, more training data alone is unlikely
to enable MLNs to match the accuracy of other CC
algorithms for this kind of data, and overfitting may
be a problem with the discriminative learning.
Execution Time: Our implementations are not all op-
timized for speed, but we can discuss approximate
values. For example, on Cora with fifty attributes,
discriminative MLN learning took about 10 minutes,
while generative learning took 3 minutes. In contrast,
the classifier used by ICA
C
and Gibbs can be learned
in a single pass over the data, and thus required about
10 seconds for learning. For inference, the MLNs re-
quired 30 seconds to 5 minutes, with only MCSAT
sometimes needing more than 2 minutes, while the
non-MLNs needed about 10 seconds (for ICA
C
) and 5
minutes (for Gibbs). Thus, MLN time is usually dom-
inated by learning, which is about one or two orders of
magnitude slower than the learning for the non-MLN
algorithms, with discriminative MLN learning being
the slowest.
4.2 Lessons Learned and Ablation
Studies
The previous section described how MLNs were able
to perform effective CC, outperforming relational-
only algorithms like MRW and simple CC algorithms
like ICA. Given the power of MLNs, we expected a
priori for this to be an easy result to obtain. In prac-
tice, it took many hours of experimentation to obtain
MLN results that were competitive with algorithms
like ICA, and the results still lagged that of algorithms
like ICA
C
. This section describes our lessons learned
and gives more details on how the MLNs were used.
We do this to enable replication, to assist others that
wish to use MLNs, and to demonstrate some of the
complexity that using MLNs entails. Some of these
lessons learned were already known but not clearly
stated in the literature, while others are, to the best
our knowledge, original observations.
To demonstrate the performance impact of these
lessons learned, Table 5 compares the performance of
different variations of the MLN rules or MLN algo-
rithms used, for the two best MLN algorithms on the
representative datasets. Note that in the results re-
ported elsewhere in this paper, the settings used for
the learning procedure and for the MLN link rules
varied based on which dataset and/or algorithm was
being used (details are given below). Thus, to facili-
tate proper comparison, Table 5 highlights in bold the
accuracy value corresponding to these default settings
for each dataset/algorithm pair. For instance, we used
a default MLN link rule called c,c for Cora but called
+c1,+c2 for WebKB-direct; hence, the value in row
A is highlighted for Cora but in row C for WebKB-
direct.
Choice of MLN Rules: Picking appropriate link-
based MLN rules is essential. Ideally, we would use a
rule like
class(o1,+c1) ˆ LinkTo(o1,o2) => class(o2,+c2)
to handle an arbitrary link from object o1 to object
o2. Here the plus sign indicates that different weights
should be learned for every sensible combination of
the values for variables c1 and c2 (e.g., 25 different
weights if there are five possible class labels). This
+c1,+c2 rule potentially captures rich linking pat-
terns, such as those previously described for WebKB-
direct. Alternatively, the simpler rule
class(o1,+c) ˆ LinkTo(o1,o2) => class(o2,+c)
indicates that only 5 weights should be learned, one
for each class label. This +c,+c rule only captures ho-
mophilic dependencies, where objects with the same
label link to each other, but allows for the strength of
the homophily to vary between different labels. We
found, however, that both of these rules were often too
challenging for any of the MLN algorithms to effec-
tively learn weights for, leading to poor accuracy. In-
stead, we found that that the rule that performed best
for most datasets was the simplest rule
class(o1, c) ˆ LinkTo(o1,o2) => class(o2, c)
ICAART 2012 - International Conference on Agents and Artificial Intelligence
12
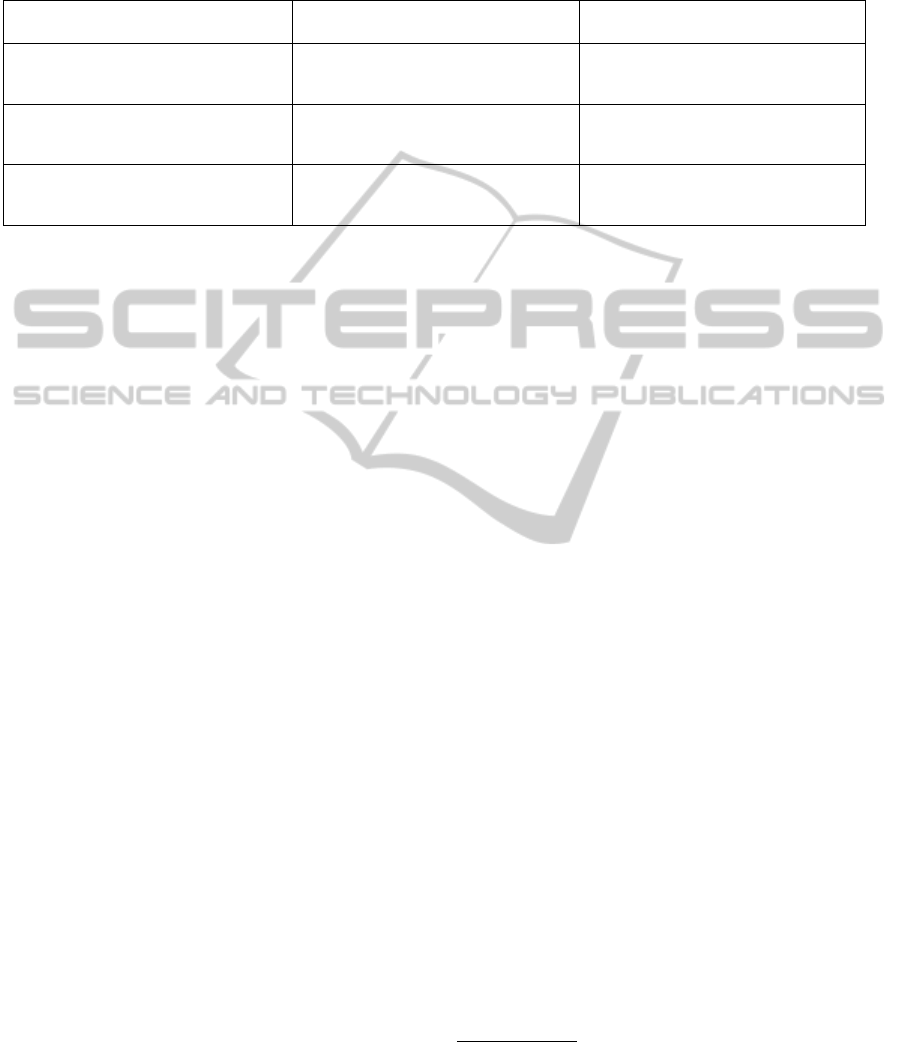
Table 5: Results of different learning and inference variants for Cora, synthetic data (with dh = 0.7 and ap = 0.4), WebKB-
direct, and WebKB-co; all with l p = 10%. For the real data, results are averaged over runs with 10 and 20 attributes. Results
with Citeseer showed very similar trends to those shown with Cora. Within each vertical group of three, the emphasized value
indicates the default setting that was used for that algorithm/dataset for all other experiments in this paper; note that unlike
the other tables, this bold value is not necessarily a maximal value.
MCSAT-d inference MCMC-d inference
Cora Syn. Web-dir.Web-co Avg. Cora Syn. Web-dir. Web-co Avg.
A.) c,c link rule 62.1 60.9 46.3 41.5 52.7 60.8 67.7 46.1 56.0 57.7
B.) +c,+c link rule 41.3 57.0 49.5 39.0 46.7 36.1 61.4 49.8 53.9 50.3
C.) +c1,+c2 link rule 15.4 25.3 51.3 19.0 27.7 16.9 24.4 56.6 37.8 33.9
D.) Learn w/o mutex; infer w/ mutex 62.1 60.9 51.3 41.5 53.9 41.0 47.2 45.8 56.4 47.6
E.) Learn & infer w/o mutex. 60.1 59.8 53.8 47.6 55.3 60.8 67.7 56.6 56.0 60.3
F.) Learn & infer w/ mutex. 49.8 65.6 51.6 21.0 47.0 35.6 48.5 42.3 41.0 41.8
G.) Learn w/ DN alg. 62.1 60.9 51.3 41.5 53.9 60.8 67.7 56.6 56.0 60.3
H.) Learn w/ PSCG alg. 61.5 59.0 46.7 42.8 52.5 61.3 68.6 53.2 56.3 59.8
I.) Learn w/ VP alg. 39.1 44.0 48.7 46.0 44.4 39.2 46.7 48.2 44.8 44.7
bww bww bww bww bww bww bww bww bww bww bww
which learns only one weight that is shared across all
labels.
Based on our initial observations of these prob-
lems, we chose to use the simplest c,c rule for all
datasets except WebKB-direct. For the latter dataset,
we used the most complex rule, +c1,+c2, because
this dataset is known to have more complex link-
ing pattern, and prior work had used this same rule
for WebKB (Lowd and Domingos, 2007; Huynh and
Mooney, 2009). Rows A, B, and C of Table 5 demon-
strate that, in most cases, these choices appear to have
been about optimal. In general, using more complex
rules leads to decreased accuracy (e.g., decreasing
from 62.1% to 41.3% to 15.4% for Cora with MC-
SAT). For WebKB-direct, however, the most complex
rule leads to the best performance. This is somewhat
sensible, due to the link patterns discussed above,
but still requires future work to determine why learn-
ing was successful for this complex rule for WebKB-
direct but not for the other datasets.
Mutual Exclusion: Many learning algorithms en-
force a mutual exclusion principle, where each object
has only one true, correct label. In Alchemy, this is
not automatically true, but the following syntax
class(o, c!)
can be used as a shorthand to indicate that, for ev-
ery object o, class(o, c) should be true for ex-
actly one value of the class label c. This syntax is
used both to concisely represent the mutual exclusion
constraint (henceforth, the “mutex”) and internally to
avoid degenerate inference problems that would oth-
erwise arise from such hard constraints (particularly
for algorithms based on MCMC). However, we found
that using the mutex usually yielded poor accuracies,
as shown by row F of Table 5. For generative learn-
ing, the poor accuracies were due to the failure of the
numerical optimizer L-BFGS-B on most datasets. We
found that removing the mutex improved the accura-
cies dramatically for generative learning, and notice-
ably for discriminative learning (see row E).
3
(The
synthetic data with MCSAT shown here was an ex-
ception; it performed better with the mutex included,
but this was not consistent across the other synthetic
variants shown in Table 3.) Since the problem seemed
to involve learning, we also considered a variant that
learned without the mutex but then added the mu-
tex for inference (see row D). In preliminary exper-
iments, this variant seemed to perform best for ev-
ery algorithm except MCMC. Thus, our default for all
other experiments in this paper was to learn without
the mutex, then perform inference without the mutex
for MCMC (like row E) but with the mutex for the
other algorithms (like row D). For MCSAT, the re-
sults in Table 5 actually show slightly better average
accuracy using the technique of row E for some real
datasets, suggesting that our initial choice may have
been slightly sub-optimal, at least for MCSAT.
Choice of Learning Algorithm: We consid-
ered three prominent discriminative learning algo-
rithms: voted perceptron (VP), preconditioned scaled
conjugate gradient (PSCG), and diagonal Newton
(DN). VP was the first discriminative algorithm for
MLNs (Singla and Domingos, 2005), while PSCG
and DN were proposed later by (Lowd and Domingos,
2007). Because Lowd and Domingos found PSCG to
perform best, it has been the primary algorithm used
by later work and is the default learning algorithm
used by Alchemy. In preliminary experiments, how-
ever, we found that DN performed slightly better than
PSCG, and so we used DN as the default discrimina-
tive learning algorithm. Table 5 shows that DN (row
3
The problems with learning while using the mutex may
be a bug in Alchemy (Hoifung Poon, personal communica-
tion). In any case, it illustrates both the promise of MLNs to
express complex relationships and the challenge of obtain-
ing good results in the context of this complexity.
INVESTIGATING MARKOV LOGIC NETWORKS FOR COLLECTIVE CLASSIFICATION
13

G) did perform slightly better on average than PSCG
(row H), and substantially better than VP (row I).
Unit Clauses: We found that learning was also af-
fected by the inclusion of appropriate rules such as
class(o,+c)
attr_1(o,+v)
which are known as “unit clauses.” The weights
learned for these rules capture general prior informa-
tion, such as the a priori probability that, for an ar-
bitrary object o, class will have value Student or
attr 1 will have the value true. Such unit clauses
have obvious corollaries in other probabilistic for-
malisms, and are mentioned in some prior work with
MLNs (Richardson and Domingos, 2006; Poon and
Domingos, 2006; Huynh and Mooney, 2009). Indeed,
the Alchemy tutorial
4
(Section 5.1) states that they
are added automatically during learning. However,
we found that the unit clauses that were automatically
added by Alchemy were not equivalent to those de-
scribed above. In addition, adding these unit clauses
manually increased accuracy by 0-12% for generative
learning and had smaller, mixed effects for discrim-
inative learning. We included these unit clauses by
default.
4.3 Limitations
Except for WebKB-direct, we studied datasets that
mostly exhibit fairly simple patterns of homophily.
This is similar to prior studies of CC, but may not
be the most favorable setting for MLNs. Future work
should perform similar comparisons on a wider range
of data with complex relationships.
As with other work on CC (Huynh and Mooney,
2009; Chechetka et al., 2010; Dhurandhar and Do-
bra, 2010), we did not attempt to use cross-validation
to select an appropriate learning rate (which affects
step size) for the discriminative algorithms, as done
by (Lowd and Domingos, 2007); conceivably this
or related tuning could further improve performance.
However, the current version of Alchemy ignores
manually-specified learning rates, and instead has
been tuned to independently select a step size.
In this paper, we used obvious MLN rules for text
classification and collective classification, and auto-
matically learned weights. Conceivably, performance
might be improved by manually encoding additional
domain knowledge in the MLN rules or via expert
assignment of weights. To address the former idea,
we explored automated structure learning based on
both the beam-search provided with Alchemy and
the bottom-up approach of (Mihalkova and Mooney,
2007). Even with the simple synthetic data, however,
4
http://alchemy.cs.washington.edu/tutorial/
these approaches either did not discover sensible rules
or ran out of memory. Future work should examine
if more recent (and efficient) structure learning pro-
posals (e.g., (Kok and Domingos, 2010)) could yield
greater success, though the results of Table 5 suggest
that improvement may be difficult to obtain.
5 CONCLUSIONS
MLNs are a powerful formalism that have been suc-
cessfully used for many tasks, and can express the
probabilistic rules needed for many more. In this pa-
per, we focused on one particular application, object-
based collective classification, where MLNs were ex-
pected to do well. Indeed, a few previously pub-
lished papers had shown that MLNs could perform
such CC and obtain reasonable-looking results, but
they had not been adequately compared with exist-
ing state-of-the-art CC techniques. We thus evaluated
MLNs on a range of real and synthetic data, using
the most prominent learning and inference algorithms
from prior work.
Overall, our results suggest that the additional
complexity (and execution time) of MLNs may not
be worthwhile for CC when the data exhibits sim-
ple patterns of homophily (a common real-world phe-
nomenon). Indeed, the MLN-based algorithms gen-
erally lagged the accuracy of previously studied CC
techniques such as ICA
C
and Gibbs, though they out-
performed the simpler ICA. These results imply that,
in terms of accuracy, the MLNs tend to behave in-
between the “cautious algorithms” described by (Mc-
Dowell et al., 2009) (represented by ICA
C
and Gibbs)
and the “non-cautious algorithms” (represented by
ICA), at least for the experimental conditions we con-
sidered here. This is somewhat surprising, since the
MLN algorithms perform inference as sophisticated
as any of the cautious algorithms described by Mc-
Dowell et al., and suggests that the problem may lie
more with learning than with inference.
On the other hand, for the one dataset with the
most complex linking patterns (WebKB-direct), the
MLN algorithms performed very well: both MCMC
and MCSAT with discriminative learning outper-
formed all baseline algorithms, regardless of the frac-
tion of known labels in the test set. This performance
required that the MLNs use the most complex linking
rule (+c1,+c2), which performed very poorly for all
of the other datasets. Perhaps MLNs are most use-
ful when the data is most complex? Unfortunately,
further results (not shown) show that the difficulties
we described in Section 4.2 with getting MLNs to
perform well can arise even with WebKB. In partic-
ICAART 2012 - International Conference on Agents and Artificial Intelligence
14

ular, starting from a baseline with direct links, we
tried learning models that included rules for the di-
rect links and rules for the co-citation links. The non-
MLN algorithms used the extra information to im-
prove (e.g., from 52.7% to 69.5% for ICA
C
), but the
best MLN algorithm (MCMC) actually lost accuracy
(from 56.6% to 45.0%). Thus, given data with com-
plex links, MLNs may sometimes outperform other
techniques, but at other times may struggle with learn-
ing based on a complex rule set.
These observations suggest that MLN learning re-
mains a challenging problem, at least for CC and
likely for other tasks as well. Future work should fur-
ther consider the impact of training set size on MLN
learning, explore the effects of MLN structure learn-
ing, and evaluate other recent weight learning algo-
rithms (e.g., (Huynh and Mooney, 2009)) for MLNs.
ACKNOWLEDGEMENTS
Thanks to David Aha, Bryan Auslander, Ryan Rossi,
and the anonymous referees for comments that helped
to improve this work. Portions of this analysis were
conducted using Proximity, an open-source software
environment developed by the Knowledge Discov-
ery Laboratory at the University of Massachusetts
Amherst (http://kdl.cs.umass.edu/proximity/). This
work was supported in part by the U.S. National Sci-
ence Foundation under award number 1116439.
REFERENCES
Chakrabarti, S., Dom, B., and Indyk, P. (1998). Enhanced
hypertext categorization using hyperlinks. In Proc. of
the ACM SIGMOD International Conference on Man-
agement of Data.
Chechetka, A., Dash, D., and Philipose, M. (2010). Rela-
tional learning for collective classification of entities
in images. In AAAI-10 Workshop on Statistical Relat.
AI.
Crane, R. and McDowell, L. K. (2011). Evaluating markov
logic networks for collective classification. In Proc.
of the 9th MLG Workshop at the 17th ACM SIGKDD
Conference on Knowledge Discovery and Data Min-
ing.
Dhurandhar, A. and Dobra, A. (2010). Collective vs inde-
pendent classification in statistical relational learning.
In Submitted for publication.
Gallagher, B., Tong, H., Eliassi-Rad, T., and Faloutsos,
C. (2008). Using ghost edges for classification in
sparsely labeled networks. In Proceeding of the 14th
ACM SIGKDD International Conference on Knowl-
edge Discovery and Data Mining.
Huynh, T. and Mooney, R. (2009). Max-margin weight
learning for markov logic networks. In Proc. of the
European Conf. on Machine Learning and Knowledge
Discovery in Databases, ECML PKDD.
Jensen, D., Neville, J., and Gallagher, B. (2004). Why col-
lective inference improves relational classification. In
Proc. of the 10th ACM SIGKDD International Confer-
ence on Knowledge Discovery and Data Mining.
Kok, S. and Domingos, P. (2010). Learning markov logic
networks using structural motifs. In Proc. of the 27th
International Conference on Machine Learning.
Kok, S., Sumner, M., Richardson, M., Singla, P., Poon,
H., and Domingos, P. (2006). The Alchemy system
for statistical relational AI (Technical Report). Depart-
ment of Computer Science and Engineering, Univer-
sity of Washington, Seattle, WA.
Lin, F. and Cohen, W. W. (2010). Semi-supervised classifi-
cation of network data using very few labels. In Proc.
of the Int. Conference on Advances in Social Network
Analysis and Mining (ASONAM).
Lowd, D. and Domingos, P. (2007). Efficient weight
learning for markov logic networks. In In Proc. of
the Eleventh European Conference on Principles and
Practice of Knowledge Discovery in Databases.
Macskassy, S. and Provost, F. (2007). Classification in net-
worked data: A toolkit and a univariate case study.
Journal of Machine Learning Research, 8:935–983.
McDowell, L., Gupta, K., and Aha, D. (2009). Cautious col-
lective classification. The Journal of Machine Learn-
ing Research, 10:2777–2836.
McDowell, L. K., Gupta, K. M., and Aha, D. W. (2007).
Cautious inference in collective classification. In
Proc. of the 22nd AAAI Conference on Artificial In-
telligence.
Mihalkova, L. and Mooney, R. (2007). Bottom-up learning
of Markov logic network structure. In Proc. of the
24th International Conference on Machine Learning.
Mihalkova, L., Moustafa, W., and Getoor, L. (2011). Learn-
ing to predict web collaborations. In Workshop on
User Modeling for Web Applications (UMWA-11).
Neville, J. and Jensen, D. (2000). Iterative classification in
relational data. In AAAI Workshop on Learning Statis-
tical Models from Relational Data.
Neville, J. and Jensen, D. (2007). Relational dependency
networks. Journal of Machine Learning Research,
8:653–692.
Poon, H. and Domingos, P. (2006). Sound and efficient
inference with probabilistic and deterministic depen-
dencies. In Proc. of the 21st AAAI Conference on Ar-
tificial Intelligence.
Richardson, M. and Domingos, P. (2006). Markov logic
networks. Machine Learning, 62(1-2):107–136.
Riedel, S. and Meza-Ruiz, I. (2008). Collective seman-
tic role labelling with markov logic. In Proc. of the
Twelfth Conference on Computational Natural Lan-
guage Learning, CoNLL ’08.
Sen, P., Namata, G., Bilgic, M., Getoor, L., Gallagher, B.,
and Eliassi-Rad, T. (2008). Collective classification in
network data. AI Magazine, Special Issue on AI and
Networks, 29(3):93–106.
Singla, P. and Domingos, P. (2005). Discriminative training
of Markov logic networks. In Proc. of the National
Conference on Artificial Intelligence.
INVESTIGATING MARKOV LOGIC NETWORKS FOR COLLECTIVE CLASSIFICATION
15
