PREDICTION OF SIGNIFICANT CRUCIFORM STRUCTURES

FROM SEQUENCE IN TOPOLOGICALLY CONSTRAINED DNA

A Probabilistic Modelling Approach

Matej Lexa

, Lucie Navr´atilov´a

, Karel Nejedl´y

and Marie Br´azdov´a

Dept Information Technology, Masaryk University, Botanick´a 68a, 60200 Brno, Czech Republic

Institute of Biophysics, Czech Academy of Sciences v.v.i., Kr´alovopolsk´a 135, 61265 Brno, Czech Republic

Keywords:

Cruciforms, Simulation, Model, Stability, DNA, Superhelicity.

Abstract:

Sequence-dependent secondary DNA structures, such as cruciform or triplex DNA, are implicated in regula-

tion of gene transcription and other important biological processes at the molecular level. Sequences capable

of forming these structures can readily be identiﬁed in entire genomes by appropriate searching techniques.

However, not every DNA segment containing the proper sequence has equal probability of forming an alter-

native structure. Calculating the free energy of the potential structures provides an estimate of their stability in

vivo, but there are other structural factors, both local and non-local, not taken into account by such simplistic

approach. In is paper we present the procedure we currently use to identify potential cruciform structures in

DNA sequences. The procedure relies on identiﬁcation of palindromes (or inverted repeats) and their evalua-

tion by a nucleic acid folding program (UNAFold). We further extended the procedure by adding a modelling

step to ﬁlter the predicted cruciforms. The model takes into account superhelical density of the analyzed seg-

ments of DNA and calculates the probability of cruciforms forming at several locations of the analyzed DNA,

based on the sequences in the stem and loop areas of the structures and competition among them.

1 INTRODUCTION

Textbook descriptions of DNA structure and func-

tion often focus on the canonical B-DNA structure

and the gene-coding properties of DNA molecules.

The famous helical structure can exist for virtually

all possible sequences of nucleotides, some of which

code for biologically active RNA molecules or pro-

teins. However, many other sequences of nucleotides

found in real DNA molecules are non-coding. Cer-

tain nucleotide sequences have the potential to ex-

ist in non-canonical structural conformations, having

their own biological function attributable directly to

the DNA-molecule and its shape, rather than to its in-

formation content. The non-canonical structures and

their functions are of great interest to molecular biol-

ogists. They can be divided into duplex, triplex and

quadruplex structures, depending on the number of

DNA strands interacting together to form a higher-

order structure (Sinden, 1994).

The best known duplex structure, cruciform DNA,

exists in locations with inverted repeats (or palin-

dromes). Thanks to the presence of a palindromic

sequence, each strand can form a duplex of its own,

resulting in the formation of two stem-loop structures

opposite to each other (Brazda et al., 2011). In DNA

molecules with similar palindromes in tandem, a vari-

ation of this structure, called slipped DNA, can form.

Here each strand forms its duplex in a different part

of the tandemly repeated set of palindromes. Triplex

structures are similar to cruciforms or slipped DNA,

but one of the two duplexes melts and contributes one

strand to the other duplex, attaching to it via Hoog-

steen base-pairing. Quadruplex DNA seems to be a

structure speciﬁc for chromosome telomeres, partic-

ipating in maintaining the stability of chromosome

ends throughout cell cycles (Neidle, 2002).

An interesting feature of all non-canonical struc-

tures is their sequence-dependency. In current

decades, molecular biologists have gained access to

sequences of entire genomes of various organisms.

The newly sequenced genomes get annotated, mostly

by identifying coding sequences and the function of

their gene products. To fully understand all the func-

tions residing in the genomes, we need to be able

to understand the functions of non-coding sequences

as well. Recent research has shown, that many non-

coding regions of human DNA contain ultraconserved

124

Lexa M., Navrátilová L., Nejedlý K. and Brázdová M..

PREDICTION OF SIGNIFICANT CRUCIFORM STRUCTURES FROM SEQUENCE IN TOPOLOGICALLY CONSTRAINED DNA - A Probabilistic

Modelling Approach.

DOI: 10.5220/0003705701240130

In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 124-130

ISBN: 978-989-8425-90-4

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

sequences, likely to be very important components of

human cells. It is speculated, that the function of these

ultraconserved sequences may be regulatory (Pennac-

chio et al., 2006). In our laboratories, we combine ex-

perimental approachesof searching for non-canonical

DNA (especially in the context of p53 gene regu-

lation) with in-silico methods of identifying palin-

dromes of certain type and evaluating their capacity

for cruciform and triplex formation.

The process of searching entire genome sequences

for cruciform- and triplex-forming segments can be

done in several stages (see also (Lexa, 2011)). As

a ﬁrst step, we identify all approximate palindromes

over a predetermined quality threshold in the se-

quence. This is done using an implementation of

a modiﬁed Landau-Vishkin algorithm with sufﬁx ar-

rays, possibly using FPGA hardware to accelerate the

search (Martinek and Lexa, 2008). Subsequently, the

candidate palindromes are evaluated for their capacity

for alternative structure formation. We use UNAFold

(Markham and Zuker, 2008), a program that can ﬁnd

optimal pairing of nucleotides in nucleic acid strands

and calculate the free energy of the resulting struc-

tures. We expected the structures with the lowest free

energy to be present in vivo, but as will be explain in

the proposed model, this may not always be the case.

In search for a beter explanation of cruciform

formation, we realized, that the existence of cruci-

form DNA may not only be determined localy, by

the sequence of nucleotides present at the site in

question, but also non-locally, by the state of neigh-

bouring DNA segements. This would be especially

true in topologicaly constrained DNA, such as cir-

cular plasmids or genomic DNA anchored to other

cell structures. In such situations, DNA exists in

a deﬁned topological state that can be characterized

by superhelical density. Superhelical density deﬁnes

how close the DNA is to a relaxed state in which the

two strands in the helix make a full turn around each

other about every 10.5 nucleotides (Sinden, 1994).

DNA with negative superhelical density posseses free

energy that can drive reactions requiring melting of

the two strands. Experiments have shown that cruci-

form DNA forms preferentially at negative superheli-

cal densities below -0.05 (Singleton and Wells, 1982).

However, the formation of cruciform DNA immedi-

ately changes the superhelical density of the residual

segments in the given topological domain, making it

less likely for other cruciform structures to form. It is

this problemwe decided to treat mathematicaly, creat-

ing a probabilistic model that can be used to calculate

the likelihood of a given DNA segment to exist in the

canonical or non-canonical structure. At the moment

we do not have enough data to calibrate the model for

general use. The main focus of the paper will be on

the inner workings of the model, using a simple nu-

clease experiment with plasmid DNA as an example

illustrating possible use of the model.

2 MATERIALS AND METHODS

2.1 The Model

The topological state of a given DNA molecule is best

described by the number of superhelical twists (W) it

adopts to accomodate any helical twists (T) that differ

from the most favored state deﬁned by linking number

of relaxed DNA (L

)

= N/10.5 (1)

where N is the number of nucleotides in the given

molecule. As long as the ends of the DNA molecule

are ﬁxed (either by circularization or attachment to

matrix), the linking number (L) can not change and

the three values remain dependent on each other ac-

cording to the following equation

L = T + W (2)

The superhelical density of such molecule is then de-

ﬁned as the number of superhelical twists per helical

twist of the molecule

σ = 10.5W/N (3)

which for most purposes is equivalent to

σ = (L− L

)/L

(4)

Historically, the ﬁrst form was used to calculate su-

perhelical density from experimentally determined

number of superhelical twists, while the second form

is more suitable when linking number, rather than

measurement is available (Sinden, 1994).

The importance of superhelical density for our

model comes from the observation that secondary

stuctures in DNA form only under favorable values

of superhelical density. One of the original measure-

ments placed the threshold value between -0.005 and

-0.006 (Singleton and Wells, 1982). We can view

the superhelical density of a molecule as a store of

free energy that can drive reactions that require partial

melting of DNA stands. The free energy of supercoil-

ing has been estimated as

∆G = (1100RT/N)(L− L

)

(5)

where R is the gas constant and T is the temperature

(Sinden, 1994). Since cruciform formation belongs

PREDICTION OF SIGNIFICANT CRUCIFORM STRUCTURES FROM SEQUENCE IN TOPOLOGICALLY

CONSTRAINED DNA - A Probabilistic Modelling Approach

125

to the category of reactions that require strand sep-

aration, we will model cruciform formation depen-

dent on the number of superhelical twists that exist or

could exist in the molecule at a given moment. When

linear DNA is converted into cruciform DNA, T de-

creases by one for every 10.5 bp participating in cru-

ciform formation (Sinden, 1994). Here we assume

that the part of the molecule that forms the new sec-

ondary structure continues to exist in a superhelicaly

relaxed state. At the same time we assume, that the

rest of the DNA molecule remains at previous super-

helical density corrected for the difference caused by

the newly formed cruciform. If the superhelical den-

sity before the formation of the cruciform was σ

old

, it

will become divided by a four-way junction into two

domains: i) the cruciform of length l with intrastrand

basepairs and ii) the rest of the molecule. Based on

Eqs. 1 and 3, the superhelical density of the rest of

the molecule will now be

new

old

∗ N + l

N − l

(6)

Using Eq. 6 for a hypothetical 1000bp plasmid with

superhelical density of -0.065 harboring a 20bp palin-

drome, after cruciform formation we obtain superhe-

lical density for the rest of the molecule

−0.065 ∗ 1000+ 20

1000− 20

−45

980

= −0.046 (7)

This clearly indicates that at the given length and su-

perhelical density, the plasmid in this example has the

potential to form only one secondary structure (cru-

ciform). Let us now suppose the plasmid contains

several palindromes capable of forming a cruciform

structure. Which of them will actually form in vivo

will most likely depend on chance. Once a cruci-

form is formed, it is very difﬁcult for it to return to

the linear form. However, if we have a population of

plasmids, as is usually the case in populations of bac-

teria or isolated molecules used in experiments, each

of them may be in a different state in terms of which

of the existing palindromes actually formed a cruci-

form. This clearly shows the need for a probabilistic

model of cruciform formation, which will not only

take into account stability of cruciform structures that

can be formed (each palindrome is a potential cruci-

form), but also the presence of other cruciforms in the

same topological domain (which will affect the resid-

ual superhelical density calculated from Eq. 6) and

the melting/folding path by which cruciforms form in

linear DNA.

The path by which a linear segment of B-DNA be-

comes cruciform DNA has been discussed intensively

in literature. C-type formation has been described in

low salt solutions and S-type formation at physiolog-

ical salt levels (Lilley, 1989). Since our model aspires

to describe conditions in vivo, we will uniformly as-

sume S-type formation in our model. Under this sce-

nario, the segment containing the palindrome has to

partially melt in a region of about 10bp in the area

of the future loop. Upon this partial melting, the free

strands can return to original conﬁguration, or form

a four-way junction initiating cruciform extrusion at

the given location. Once the cruciform is formed, ex-

tra energy is required for its transformation back to

linear B-DNA.

In our model, we divide the sequence of the palin-

drome into three zones: i) the melting zone is in the

loop area, it extends to the ﬁrst two bases that will

form a pair in the stem of the cruciform as predicted

by UNAFold, however, it is forced to be at least 9bp

long; ii) the cruciform stem zone formed by the bulk

of the paired bases and iii) the nucleation zone formed

by two paired bases at the boundary of the stem and

the loop.

Based on the available knowledge on cruciform

formation, we can now formulate a stochastic math-

ematical model of cruciform formation in a topolog-

ically isolated segment of DNA. A schematic draw-

ing of the model is given in Figure 1. We start by

identifying a set of palindromes in the DNA sequence

by computational methods. Let us designate them

p1, p2,..., p

. Each palindrome will exist in one of

three states: L (linear B-DNA), M (melted loop zone)

or C (cruciform). The transitions will be modelled

based on calculated free energies or melting temper-

atures of the appropriate duplex state. The lower the

energy (or higher the melting temperature), the less

likely the molecule will be to leave that state. The

best way to calculate the relative probabilities of tran-

sition for each palindrome remains to be determined.

Currently, we use a formula that takes into account

the exponential relationship between free energy or

melting temperature on one side and rate constants of

the underlying reactions on the other. An exponen-

tial function of free energy or temperature difference

from melting temperature is calculated for each palin-

drome and the resulting values are then normalized to

a sum of 100% to obtained the relative probabilities of

transition (refer to MATLAB (see Url 1) code for the

exact formula). The whole system can now be simu-

lated by iterating through a predeﬁned number of cy-

cles (event time). In each of the cycles the state of a

given molecule will be changed based on the calcu-

lated transition probability distribution. If calculated

on a population of molecules (or cells), we obtain per-

centages of palindromes present as linear B-DNA or

cruciform for each of the palindromes.

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

126

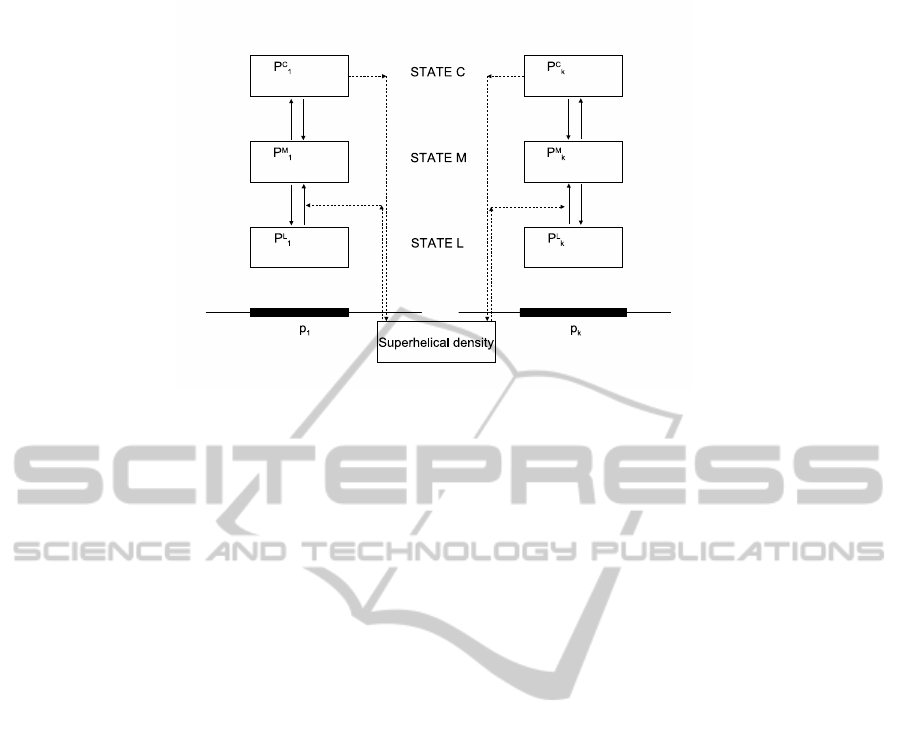
Figure 1: Model schema. Each palindrome can exist in three states (L - linear B-DNA, M - melted strands, C - cruciform).

Full arrow represent transitions between states. Dashed arrows represent dependency between variables of the model. State

M is a transition state and is not directly represented in the current version of the model.

2.2 DNA Analysis

An experimental protocol using S1 nuclease was used

to detect the presence of cruciform structures in plas-

mid DNA in vivo. S1 nuclease digestion only digests

DNA in locations with unpaired bases, such as the

loop of a cruciform structure. The plasmids used in

the experiments were additionally digested with ScaI

restriction endonuclease. A single ScaI restriction site

is present in the plasmid pBluescript SKQ II- (pBSK,

Stratagene) and its derivatives used in our experiment.

The ScaI restriction site is located at position 2510 in

the pBluescript plasmid. If no cruciforms are present,

this treatment yields a linearized plasmid. In the pres-

ence of cruciforms, it yields two fragments of DNA.

Their size is indicative of the position at which the

cruciform has formed.

Supercoiled plasmids pBluescript SK II-, pPGMI

(pBSK- containing a cloned p53 consensus site AGA-

CATGCCTAGACATGCCT (Palecek et al., 1997) and

pPGM2 (pBSK- containing a cloned p53 consen-

sus site AGACATGCCTAGACATGCCT) (Palecek et

al., 2004) were isolated from bacterial strain TOP10

(Stratagene) as described in the Qiagen protocol (Qi-

agen, Germany). SmaI restriction enzyme (Takara,

Japan) was used for linearization of pBSK, pPGMI

and pPGM2. Supercoiled plasmid DNA (2µg) was

dissolved in binding buffer (5 mM Tris-HCl pH 7.6,

0.01% Triton X-100, 1mM MgCl

and 50mM KCl)

and pre-incubated at 37

◦

C for 20 min. Plasmid DNA

was digested by S1 nuclease (4 U/µg DNA, Promega)

for 20 min at 37

◦

C in the nuclease S1 buffer (30mM

sodium acetate pH 4.6, 280mM NaCl, 1mM ZnSO4,

Promega buffer). After the cleavage, samples were

precipitated by ethanol, dissolved in the water and di-

gested by the restriction endonuclease ScaI for 90

min. The resulting DNA was visualized by elec-

trophoresis on an agarose gel.

3 RESULTS

3.1 DNA Analysis

Three plasmids used routinely in our laboratory were

submitted to S1 nuclease digestion treatment to re-

veal any unpaired DNA bases indicative of cruciform

structure. An agarose gel of plasmids pBSK-, pPGMI

and pPGM2 upon S1 nuclease and ScaI digestion is

shown in Figure 2. With no structures present, the

plasmids are only digested by ScaI. The resulting

linearized plasmids show as a single band at about

3000bp. As seen in lanes 3, 5 and 7, a signiﬁcant

percentage of plasmids were also disgested by S1 nu-

clease. The pBSK- plasmid shows a prominent pair of

bands at about 700 and 2200bp (any two bands due to

S1 nuclease treatment should add up to the total size

of the original plasmid, which is 2961 for pBSK-).

Another band at 1500bp is most likely a mixture of

two products of roughly equal size. The pPGMI plas-

mid displays a similar pattern, except for a very weak

pair of bands at 1000 and 2000bp. pPGM2 yields a

pair at 1100 and 1800bp, which corresponds to a cru-

ciform in the cloning site. Surprisingly, the other pairs

of bands found in both pBSK- and pPGMI are ab-

sent and most of the plasmid is found in its linearized

form.

3.2 Example of Model Use

To demonstrate the use of the model, we analyzed

the sequences of three plasmids, pBSK-, pPGMI and

PREDICTION OF SIGNIFICANT CRUCIFORM STRUCTURES FROM SEQUENCE IN TOPOLOGICALLY

CONSTRAINED DNA - A Probabilistic Modelling Approach

127

Figure 2: S1 nuclease treatment. Plasmids pBSK, pPGMI and pPGM2 show the presence of distinct bands indicative of

S1-sensitive sites. Substracting 450 from the size of the band gives the location of the digested position in the plasmid.

pPGM2 for approximate palindromes by scanning it

with our implementation of the Landau-Vishkin algo-

rithm (Martinek and Lexa, 2008). The most promi-

nent palindromes are listed in Table 1. The optimal

basepairing in these sequences was calculated with

UNAFold. Free energy for each structure is reported

in the fourth column of the table. At this moment we

could simply choose the locations with the lowest free

energy and assume this will be the palindrome to form

a cruciform. In reality, a subset of these locations will

have cruciforms present. We deployed the model to

see if it can choose a subset that correlates with the

results of the experiment.

An implementationof the model in MATLAB (see

Url 1) was initialized using the data in Table 1, the

size of the DNA segment to be analyzed and its su-

perhelical density. During the simulation, palindrome

sequences change states according to the calculated

transition probability functions. Results of a simula-

tion with 1000 molecules of DNA for the three plas-

mids for a range of critical parameter settings are

shown in Table 2. We also visualized the values in

respect to experimental results and the free energies

in Figure 3.

4 DISCUSSION

We designed an event-based stochastic mathemati-

cal model of cruciform formation. Several simplify-

ing assumptions had to be made. Most importantly,

the effect of residual superhelical density in the cur-

rent model is all or none, represented by a thresh-

old value of -0.05 above which no cruciform forma-

tion is possible in the simulated molecules. The real

effect is likely to be less abrupt. However, we be-

lieve we can nevertheless observe the expected ef-

fects in a qualitative manner. Looking at the results

of simulations in Table 2 we can notice interesting

behavior of the model that reﬂects its ability to re-

solve some of the problems posed by the experimen-

tal data. The preferential prediction of cruciforms at

p3 and p7 is in full agreement with S1 nuclease treat-

ment results for pBSK- and pPGMI. The results for

pPGM2 are both, difﬁcult to understand, and difﬁcult

to explain by the model. There are less than a dozen

nucleotide differences between pPGMI ands pPGM2,

still it seems the cloned palindrome totally overshad-

owed the pBSK-inherent capacity for cruciform for-

mation. For now, we have no explanation for this

phenomenon. Regarding our model, changing ini-

tial superhelical density from -0.065 to a higher value

causes a shift from longer to shorter palindromes. In

special cases, this mechanism could cause imperfect

palindromes to contribute to cruciform formation. We

also changed the ability of the modelled cruciforms to

form reversibly. Less stable cruciforms were allowed

to disintegrate at a rate proportional to the stability

of the structure. In a hybrid version of the model,

this behavior was only allowed at higher values of

residual superhelical density. We observed accumu-

lation of cruciforms that kept the superhelical den-

sity above the disintegration threshold. Whether such

mechanism plays any role in real molecules is not

known. In summary, our model predicts cruciform

formation that is in partial agreement with the few

experiments we have at hand at the moment. Future

improvements should include better theoretical treat-

ment of transition probability calculation, less abrupt

thresholds for DNA behavior dependent on superhe-

lical density and most of all thorough validation and

calibration of the model on experimental data. The

model could prove useful for annotating approximate

palindromes in whole genomes, considering their im-

portance in biological processes based on the likeli-

hood of cruciform formation at different superhelical

densities of the given segment of DNA.

ACKNOWLEDGEMENTS

We wish to thank O. Lexa for invaluable help with

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

128

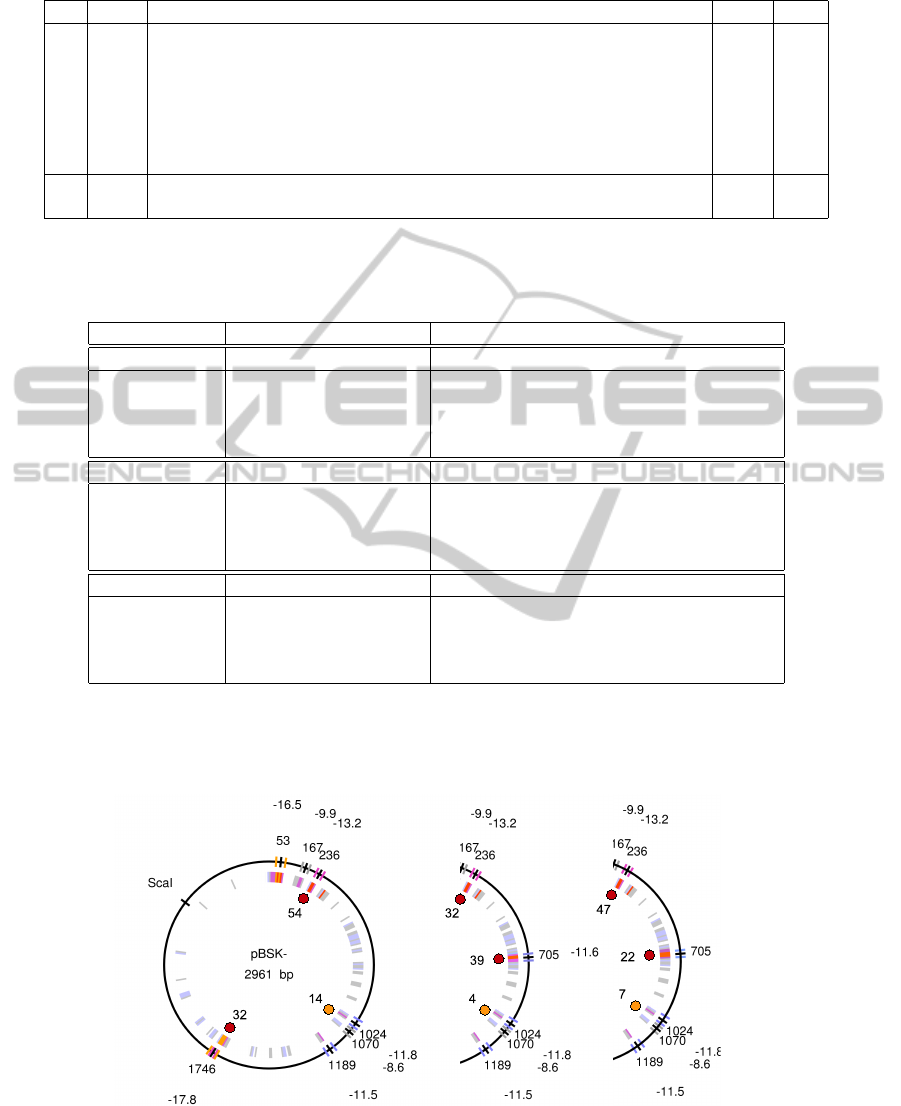
Table 1: Palindromes.

ID POS SEQUENCE dG T

p1 53 GGCGGGTGTGGTGGTTACGCGCAGCGTGACCGCTACACTTGCC -16.5 38.0

p2 167 CTAAATCGGGGGCTCCCTTTAGGGTTCCGATTTAGT -9.9 78.0

p3 236 AGGGTGATGGTTCACGTAGTGGGCCATCGCCCT -13.2 28.0

p4 1025 GCGGGGAGAGGCGGTTTGCGTATTGGGCGCTCTTCCGCTTCCTCGC -11.8 84.0

p5 1070 CTCGCTGCGCTCGGTCGTTCGGCTGCGGCGAG -8.6 70.0

p6 1189 GCCAGCAAAAGGCCAGGAACCGTAAAAAGGCCGCGTTGCTGGC -11.5 54.0

p7 1746 GCAAACAAACCACCGCTGGTAGCGGTGGTTTTTTTGTTTGC -17.8 30.0

p8 705 AAGCTTAAGGCATGTCTAGGCATGTCTAAGCTT -11.6 30.0

p9 705 AAGCTTAAGACATGCTCAGGCATGTCTGGGCTT -11.8 32.0

The most prominent approximate palindromes in the sequence of pBSK- and its derivatives pPGMI and pPGM2. Palindromes p8 and p9 are

from sequences that were cloned into pBSK- to form the two other plasmids.

Table 2: The results.

σ formation only p1 p2 p3 p4 p5 p6 p7 p8/p9

pBSK-(EXP) 0 0 20 0 5 0 20 -

pBSK-(SIM1) -0.065 no 7 0 6 0 0 0 84 -

pBSK-(SIM2) -0.060 no 0 2 75 0 1 0 0 -

pBSK-(SIM3) -0.063 yes 0 4 23 0 2 0 71 -

pBSK-(SIM4) -0.063 hybrid 0 0 54 0 14 0 32 -

pPGMI(EXP) 5 0 20 0 5 0 20 0

pPGMI(SIM1) -0.065 no 4 0 7 0 0 0 83 6

pPGMI(SIM2) -0.060 no 0 1 57 0 1 0 0 27

pPGMI(SIM3) -0.063 yes 0 2 32 0 3 0 45 18

pPGMI(SIM4) -0.063 hybrid 0 0 32 0 4 0 25 39

pPGM2(EXP) 0 0 0 0 0 0 0 10

pPGM2(SIM1) -0.065 no 8 0 6 0 0 0 82 2

pPGM2(SIM2) -0.060 no 0 1 62 0 0 0 0 18

pPGM2(SIM3) -0.063 yes 0 3 17 0 3 0 64 13

pPGM2(SIM4) -0.063 hybrid 0 0 47 0 7 0 24 22

The results of simulations (SIM1-SIM4) are compared with results of S1 nuclease digestions (EXP). Experimental values (%) were

estimated by visual inspection of Figure 2. Hybrid cruciform treatment allowed cruciform disintegration only at residual superhelical

densities above -0.052. Note: p3 and p7 cannot be distinguished from each other in the experiment, so we assigned them equal values of

20%.

Figure 3: Sequence analysis and model predictions. Diagrams of the three plasmids used in the study. Inner colored

circle shows locations containing interesting approximate palindromes. Outer colored signs and labels represent the nine

palindromes selected with UNAFold, together with their positions and free energies. The dots inside the circle show the

results of our simulations (SIM4 in Table 2). The predicted cruciforms are not necessarily those with the lowest energy,

however they correspond better to the experimental results.

PREDICTION OF SIGNIFICANT CRUCIFORM STRUCTURES FROM SEQUENCE IN TOPOLOGICALLY

CONSTRAINED DNA - A Probabilistic Modelling Approach

129

MATLAB simulations. This work was supported

by the Czech Science Foundation grant 204/08/1560

and 301/10/2370 and by Institutional Research Plans

AV0Z50040507, IAA500040701, AV0Z50040702

and 1QS500040581.

REFERENCES

Brazda V., Laister R.C., et al. (2011). Cruciform structures

are a common dna feature important for regulating bi-

ological processes. BMC Molecular Biology, 12:33.

Lexa M., Martinek T., et al. (2011). A dynamic program-

ming algorithm for identiﬁcation of triplex-forming

sequences. Bioinformatics, 27:2510–2517.

Lilley, D. (1989). Structural isomerization in dna: The

formation of cruciform structures in supercoiled dna

molecules. Chemical Society Reviews, 18:53–83.

Markham, N. and Zuker, M. (2008). Unafold: software for

nucleic acid folding and hybridization. Methods in

Molecular Biology, 453:3–31.

Martinek, T. and Lexa, M. (2008). Hardware accelera-

tion of approximate palindrome searching. In The In-

ternational Conference on Field-Programmable Tech-

nolog., pages 65–72.

Neidle, S. (2002). Nucleic acid structure and recognition.

Oxford University Press.

Palecek E., Vlk D., et al. (1997). Tumor supressor protein

p53 binds preferentially to supercoiled dna. Onco-

gene, 15:2201–2209.

Palecek E., Brazda V., et al. (2004). Enhancement of p53

sequence-speciﬁc binding by dna supercoiling. Onco-

gene, 23:2119–2127.

Pennacchio L.A., Ahituv N., et al. (2006). In vivo enhancer

analysis of human conserved non-coding sequences.

Nature, 444:499–502.

Sinden, R. (1994). DNA structure and function. Academic

Press.

Singleton, C. and Wells, R. (1982). Relationship between

superhelical density and cruciform formation in plas-

mid pvh51. The Journal of Biological Chemistry,

257:6292–6295.

Url 1: http://www.ﬁ.muni.cz/˜lexa/cruciform/index.html

Visited Oct 2011.

BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms

130