ESTIMATING PLANAR STRUCTURE IN SINGLE IMAGES

BY LEARNING FROM EXAMPLES

Osian Haines and Andrew Calway

University of Bristol, Bristol, U.K.

Keywords:

Monocular vision, Image understanding, Single image, Plane detection, Planar structure, Scene analysis,

Learning, Nearest neighbour, Topic discovery, Latent semantic analysis, Spatiogram.

Abstract:

Outdoor urban scenes typically contain many planar surfaces, which are useful for tasks such as scene re-

construction, object recognition, and navigation, especially when only a single image is available. In such

situations the lack of 3D information makes ﬁnding planes difﬁcult; but motivated by how humans use their

prior knowledge to interpret new scenes with ease, we develop a method which learns from a set of train-

ing examples, in order to identify planar image regions and estimate their orientation. Because it does not

rely explicitly on rectangular structures or the assumption of a ‘Manhattan world’, our method can generalise

to a variety of outdoor environments. From only one image, our method reliably distinguishes planes from

non-planes, and estimates their orientation accurately; this is fast and efﬁcient, with application to a real-time

system in mind.

1 INTRODUCTION

We address the problem of detecting planes in a sin-

gle image, and estimating their 3D orientation. Man-

made environments tend to contain many planes, and

these can be used for compact representation of 3D

scenes (Bartoli, 2007) and more efﬁcient robot navi-

gation (Gee et al., 2008; Mart

ınez-Carranza and Cal-

way, 2010). The ability to discover planes from only

a single image would be beneﬁcial in tasks includ-

ing image understanding (Saxena et al., 2008), recon-

structing 3D models (Ko

seck

a and Zhang, 2005) or

wide baseline matching (Mi

ık et al., 2008).

Finding planes in single images is challenging,

due to the of lack of depth information. One popu-

lar approach is to use vanishing lines (Ko

seck

a and

Zhang, 2005) to infer the scene geometry; however,

this presupposes that such structure exists. Our ap-

proach (ﬁgure 1) is instead motivated by humans’ ap-

parent ability to understand scenes from one view: we

learn from the appearance of a set of examples, man-

ually labelled with their class and orientation; and de-

scribe these with feature descriptors in a bag of words,

enhanced with spatial information. Using these train-

ing images allows us to identify image regions as pla-

nar – for building fac¸ades, stone walls and so on –

or as non-planar – for foliage, vehicles, etc; then for

planar regions we estimate their 3D orientation.

Figure 1: For a given image region (left) our algorithm clas-

siﬁes them as planes and estimates their orientation (cen-

tre) by ﬁnding training examples with similar orientation

(right).

The method accurately separates planes from non-

planes, making a sufﬁciently conﬁdent decision in

91% of cases, with 90% accuracy; plane orientation is

predicted with a mean error of around 14° . Since we

do not rely on vanishing lines or rectangular structure,

the method is applicable to a wider range of scenes.

The method is fast, able to make a decision for a new

region in under one second. In this work we consider

only the classiﬁcation and orientation of individual

image regions – automatic detection or segmentation

is left for future work.

289

Haines O. and Calway A. (2012).

ESTIMATING PLANAR STRUCTURE IN SINGLE IMAGES BY LEARNING FROM EXAMPLES.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 289-294

DOI: 10.5220/0003708902890294

 SciTePress

The paper is organised as follows. Section 2 dis-

cusses related work, then section 3 describes the de-

tails of the method. The results in section 4 show that

the method can distinguish planes from non-planes

and reliably predict their orientation in a variety of

situations, and we conclude in section 5 with sugges-

tions for future work.

2 RELATED WORK

A standard way to obtain geometry from a single

image is the use of vanishing points – for example

(Ko

seck

a and Zhang, 2005) rely on the orthogonality

of planes to group lines and hypothesise rectangles,

from which the pose of the camera can be recovered.

Similarly, (Mi

ık et al., 2008) treat rectangle de-

tection as a labelling problem, and use the detected

planes’ orientation for wide baseline matching.

Another cue which may be exploited is the dis-

tinctive appearance of certain parts of images. The

method most similar to our own is that of (Hoiem

et al., 2007), which classiﬁes ‘super-pixels’ into ge-

ometric classes, with orientations limited to being ei-

ther horizontal, left, right, or front facing. A vari-

ety of features are used to create a coherent grouping

from the initial super-pixels, resulting in an esimate

of scene layout which has been used to create simple

3D models and for object recognition.

(Saxena et al., 2008) focus on the related task of

estimating depth, by training on range data from a

laser scanner. From absolute and relative depth esti-

mates at individual regions, a Markov Random Field

is used to ﬁnd a consistent depth map over the whole

image. This has been used for sophisticated 3D model

building, and to drive a high-speed toy car (Michels

et al., 2005).

These methods show considerable progress in un-

derstanding single images; however they either rely

on a restrictive ‘Manhattan’ assumption, or when ap-

plicable to more general scenes, can only obtain very

coarse orientation or depth.

3 METHOD

Here we give an overview of our method, with more

details in subsequent subsections. First, we gather a

database of training examples, and manually assign

a class (plane or not plane) and orientation (normal

vector). Then the class and orientation of new regions

are estimated using a K-Nearest Neighbour classiﬁer,

with similarity between regions evaluated as follows.

(a) (b) (c)

(d) (e) (f)

Figure 2: Examples of the training data we use, showing

the manually selected region of interest and plane orienta-

tion (regions (a)-(d)); examples (d) and (f) were obtained by

warping the original images.

We use histograms of oriented gradients to de-

scribe the local appearance at salient points in an im-

age region; since these are not informative enough on

their own, we accumulate information using a bag of

words approach, applying a variant of Latent Seman-

tic Analysis (Deerwester et al., 1990) for dimension-

ality reduction.

The resulting vectors of latent ‘topics’ can be used

for classiﬁcation and orientation, but performance is

improved by also considering their spatial conﬁgu-

ration, which we represent using a histogram aug-

mented with means and covariances – a ‘spatiogram’

(Birchﬁeld and Rangarajan, 2005); as far as we are

aware, using a spatiogram with a bag of words is

novel. Further technical details can be found in

(Haines and Calway, 2011).

3.1 Training Data

We collect training images of planes and non-planes

from a variety of outdoor locations; these have a res-

olution of 320 × 240 pixels, and have been corrected

for radial distortion. For each image we mark a re-

gion of interest, and assign them to the plane or non-

plane class as appropriate. To get the true orientation,

corners of a quadrilateral are marked, corresponding

to a real rectangle; this deﬁnes two orthogonal sets

of parallel lines, whose intersections deﬁne vanishing

points v

and v

. From this we calculate n, the normal

vector of the plane, using n = K

l, where l = v

× v

is the vanshing line of the plane and K is the 3 × 3

matrix encoding the camera paramters (see ﬁgure 2).

We generate more training examples, to approx-

imate planes seen from different viewpoints, by ap-

plying geometric transformations to the images. The

simplest of these is to reﬂect about the vertical axis;

we can also use the known relative pose of the planar

regions to render new views from different locations,

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

290

via the homography H = R + tn

/d, where R and t

are the rotation matrix and translation vector for the

new view, and d is the perpendicular distance to the

plane (deﬁned up to scale). H is used to warp the im-

age, to approximate the plane as seen from the new

viewpoint, while the normal vector is rotated by R. In

practice, the range of possible warps is limited by the

image resolution.

3.2 Features

Following more typical object recognition ap-

proaches, we use descriptors that describe local ori-

entations, in a histogram of oriented gradients. While

this is the basis descriptors like SIFT (Lowe, 2004),

we emphasise that our task is quite different: one of

the beneﬁts of SIFT is that it is invariant to a wide

range of deformations, whereas our aim is speciﬁcally

to determine plane orientation, not identity.

For each patch, we create gradient histograms for

each quadrant, each with 12 angular bins, and con-

catenate these to form a descriptor of 48 dimensions

– this is to capture some local structure information

and build a richer descriptor.

Feature descriptors are created at salient points in

the image, detected using the Difference of Gaussians

detector (DoG), which gives a location and scale for

each point. We use the scale to set the width of the

patch to create the descriptor; scale selection seems to

be advantageous since it ensures the most appropriate

scale is being used at each location – this is veriﬁed

by our results (see section 4), which show that multi-

scale DoG detection is consistently superior to both

single-scale DoG and FAST (Rosten and Drummond,

2006).

3.3 Bag of Words

The gradient descriptors capture information about

local areas, but are not sufﬁcient to disambiguate the

structure of the scene, so we accumulate information

over the whole region using the bag of words model.

Each image region is represented by a histogram x

over N words (typically N = 300; see section 4); term

frequency - inverse document frequency weighting is

used to down-weight common words, resulting in the

weighted word vector x

The words are found by quantising each of the D

descriptor vectors d

in the image region to a code-

book; the codebook is built by clustering descriptors

extracted from a set of typical images, using K-means

with N cluster centres.

3.3.1 Topic Discovery

When N is large, the word vector will be high dimen-

sional and sparse, and encodes no relationship bew-

teen potentially synonymous words. We overcome

this using Orthogonal Nonnegative Matrix Factorisa-

tion (ONMF) to reduce the word histogram to a vec-

tor of latent topic weights. ONMF is related to Latent

Semantic Analysis (LSA) (Deerwester et al., 1990),

but differs in that the topic vectors have non-negative

components (this is essential, see section 3.4).

ONMF factorises the term-document matrix X

(where X

n j

is the (weighted) number of occurrences

of word n in image j, for M images) into X ≈ WH,

where W is the basis of the latent topic space (of rank

T , the number of topics), and H contains the topic

vectors. Word vectors are approximated by x

≈ Wh

where h

is topic vector; conversely the topic vector

for a new word vector is h

= W

(because W is

orthogonal).

ONMF factorisation has no closed form solution,

so we use an iterative method (Choi, 2008) which

alternates the following updates (the columns of W

must be re-normalised after each iteration):

←− W

(XH

)

(WHX

(1)

←− H

WH)

(2)

3.4 Spatiograms

The constellation and star models (Fergus et al., 2005)

have shown that representing the spatial arrange-

ment of descriptors can improve performance; how-

ever because these are computationally expensive we

use spatiograms instead (Birchﬁeld and Rangarajan,

2005). A spatiogram is a higher-order generalisation

of a histogram, where each bin also has a mean and

covariance matrix, summarising the points contribut-

ing to it. A spatiogram S

word

over the words consists

of a set of N triplets s

= hh

,µ

,Σ

i, were h

is the

bin count, µ

is the mean and Σ

the covariance ma-

trix of the 2D coordinates for points contributing to

the histogram bin. These are calculated as follows

(altered so that we can use them for words, weighted

words, or topics):

∑

d=1

(3)

− β

∑

d=1

− µ

)(v

− µ

)

(4)

ESTIMATING PLANAR STRUCTURE IN SINGLE IMAGES BY LEARNING FROM EXAMPLES

291

where v

is the 2D point at which descriptor d

created, and α =

∑

d=1

, β =

∑

d=1

. For the

basic word spatiogram, the element weight λ

equal to 1 iff descriptor d quantises to word n; for

the spatiogram of weighted words S

word0

, λ

i.e. the weighted occurrence of each word in the im-

age. The topic spatiogram S

topic

(of length T ) uses

, where n is the word to which descriptor

quantises, and W

is the component of the basis

vector for topic t relating to word n. Note that all

weights must be positive – the reason we use ONMF

instead of LSA. To compare spatiograms during clas-

siﬁcation we use the distance metric proposed by (

Conaire et al., 2007). As we show in section 4, in-

cluding spatial information boosts performance con-

siderably.

3.5 Classiﬁcation

To classify image regions and estimate their orienta-

tion, we use the relatively simple K-Nearest Neigh-

bour classiﬁer (KNN), chosen because analysing the

chosen neighbours (see ﬁgures 1, 5) allows us to ver-

ify the method works as expected. Classiﬁcation and

orientation estimation can be performed simultane-

ously, by ﬁnding the K nearest neighbours: the class is

assigned to the majority class of these, and the orien-

tation is the mean of the 3D normal vectors. The pro-

portion of neighbours in the larger class can be used

as a conﬁdence value to reject less certain classiﬁca-

tions.

4 RESULTS

We collected an initial data set of 556 regions, from

an urban area. For evaluation we use ﬁve-fold cross

validation, and all tests use a value of K = 5 nearest

neighbours, chosen for its superior performance (ex-

periments omitted for brevity). First we analyse the

performance of using ONMF and spatiograms, com-

pared to the basic bag of words: we ran the algorithm

using the (weighted) word histograms x

only, on

word-spatiograms S

word0

, on topic vectors h only, and

on topic spatiograms S

topic

(the full method), for vary-

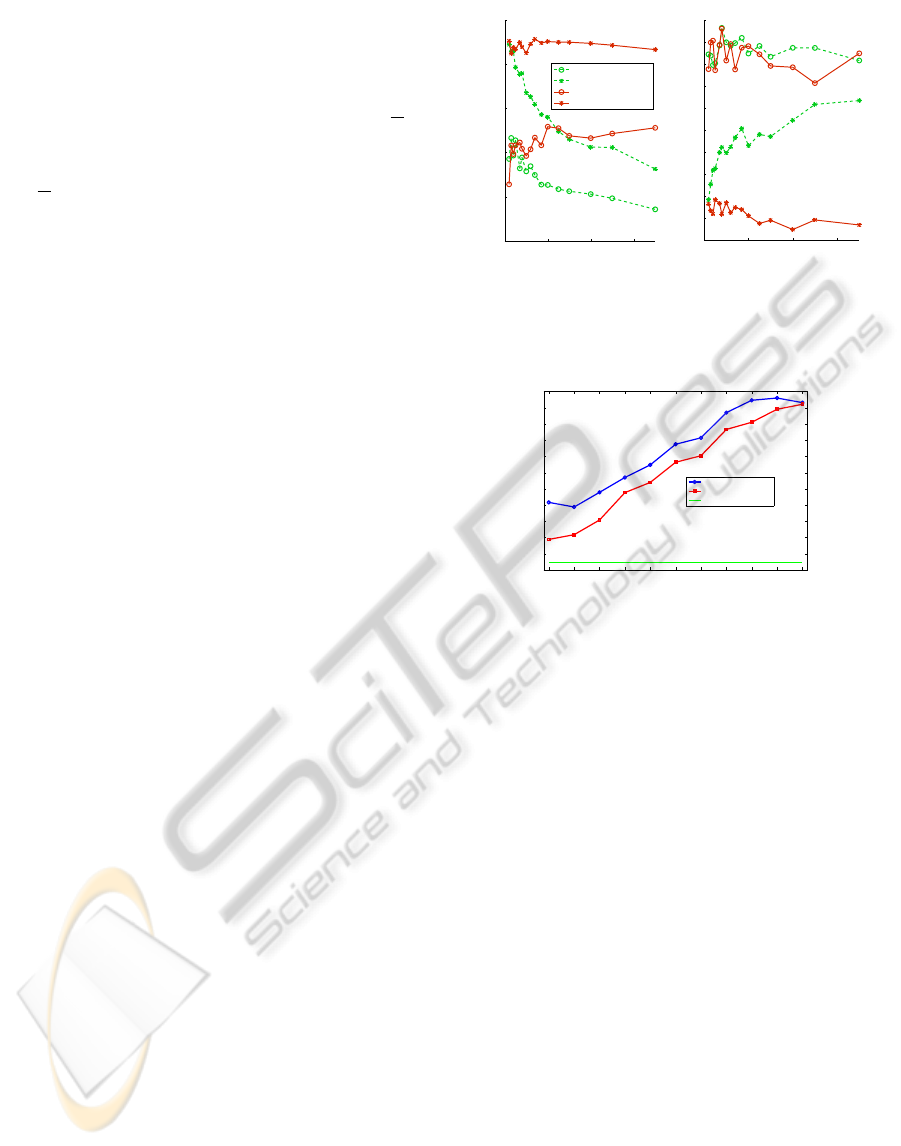
ing vocabulary size. Figure 3 shows results for classi-

ﬁcation accuracy and orientation error: in general, us-

ing topic discovery out-performs using words directly.

Performance using word histograms decreases as they

become sparser with increasing vocabulary size, but

topic vectors can extract meaningful information from

high dimensional word vectors, and performance re-

mains almost constant. The graphs also clearly show

0 200 400 600

0.65

0.7

0.75

0.8

0.85

0.9

Number of words

Classification accuracy

Word histogram

Word spatiogram

20−Topic histogram

20−Topic spatiogram

(a) Classiﬁcation accuracy.

0 200 400 600

Number of words

Orientation error (degrees)

(b) Orientation error.

Figure 3: Comparison of words and topics for different vo-

cabulary sizes.

5 10 15 20 25 30 35 40 45 50 55

Patch width

Orientation error

FAST − single scale

DoG − single scale

DoG − scale selection

Figure 4: Using the Difference of Gaussians detector to

choose the scale at which descriptors are built outperforms

any single ﬁxed scale, detected with either DoG or FAST.

the beneﬁt of using spatiograms, which outperform

histograms in all cases.

Interestingly, the results suggest that a very small

number of words can be used without topic discov-

ery – however, this constrains the method to use

only small vocabularies, while are likely to generalise

poorly to new data sets. We veriﬁed this on our in-

dependent data set (see below) and found that in this

case, using words alone gave an orientation accuracy

of 20.5° (with standard deviation 18.1°), compared to

using topics with error of 17.5° (std 15.9°).

We also ran an experiment to verify that using

scale selection for the features is important. To en-

sure that no one scale was the best with scale selection

simply choosing this occasionally, we tested scale se-

lection (using the DoG detector) against ﬁxed patch

sizes with widths from 5 to 55, detected with both

FAST and DoG; as ﬁgure 4 shows, scale selection is

always better than any one scale.

Finally, we augment the training set by reﬂecting

and warping regions (section 3.1), giving a total of

7752 (we do not test on the warped images, and en-

sure no region can match to a warped version of it-

self). This decreases the mean orientation error from

17.2° (standard deviation 13.7°) to 14.3° (std 12.9°).

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

292

Figure 5: Examples of test planes (far left) and their 5 nearest neighbours. Top: matching to neighbours with different

appearance. Bottom: accurate orientation estimation, though there are no images of the ground in the training set.

0 50 100 150

200

400

600

800

1000

1200

1400

1600

Orientation error (degrees)

Our method

Random neighbours

Figure 6: Distribution of errors for our method (dark),

showing the majority of errors are small. Comparison to

random neighbours method is superimposed (light).

For the remaining tests we use DoG for feature po-

sition and scale selection, the full set of warped exam-

ples, topic spatiograms in a vocabulary of 300 words,

and we discard regions with a conﬁdence below 0.7.

The results we obtain for this situation is a recall (per-

centage of regions above the conﬁdence threshold) of

91%, classiﬁcation accuracy of 90%, and a mean ori-

entation error of 14°. Figure 6 shows a histogram

for orientation estimation, clearly showing that for

the majority of regions (81%), the error is in the re-

gion of 0° to 20°. For comparison, and to indicate

what a mean error of 14° signiﬁes, we show resuts

of an experiment using randomly chosen neighbours

(histogram overlayed on the same plot). Clearly our

method performs much better than chance – where

the mean error is above 40°; this is a useful validation

of the method, as it shows our method is not merely

exploiting an artefact of how the data are distributed.

4.1 Independent Data

We also tested the algorithm on an independent data

set collected from a different urban area, with the data

set from above used for training. We achieved similar

performance – a recall of 91%, classiﬁcation accuracy

of 87%, and mean orientation error of 17.5°. This

set included some difﬁcult regions – some without

the classic rectangular-structure appearance (ﬁgures

1,7(d)), as well as images of pavements and roads,

while we were careful to include no images of the

ground in the training set, to test generalisation (ﬁg-

ures 5 bottom, 7(f),7(g)). Figure 5 shows some exam-

ple results of orientation estimation, alongside their

nearest neighbours: these are often quite different in

appearance, yet have a similar orientation. Figure

7 shows further examples, including non-planar re-

gions. In these images, blue (thin) arrows indicate

ground truth, and green (thicker) arrows are the esti-

mated normal, with cyan circles denoting non-planar

classiﬁcation.

Figure 8 shows cases where the method performs

poorly, for example 8(a) and 8(b) where all the neigh-

bouring planes have very different orientation, a rare

situation which requires further investigation. Figure

8(d) is a more difﬁcult example, since it is quite differ-

ent from any training images. Figure 8(e) may be con-

fused by the railings, vertical trees and strong horizon

line; and it is interesting to note that 8(f) is incorrectly

determined to be a plane, when the side of a van could

arguably be considered planar.

5 CONCLUSIONS

We have shown that we can reliably determine

whether regions of images are planar or not, and

estimate their orientation with respect to the view-

point. This is successfully achieved using information

from just one image in a bag of words representation,

where performance is improved by using latent topic

discovery and encoding spatial information. A KNN

classiﬁer was sufﬁcient to demonstrate that the algo-

rithm is able to classify a wide variety of plane and

non-plane images and accurately estimate plane ori-

entation (more advanced classiﬁers would be a nat-

ural aventue of future work); our method can work

even in examples devoid of typical structure such as

ESTIMATING PLANAR STRUCTURE IN SINGLE IMAGES BY LEARNING FROM EXAMPLES

293

(a) (b) (c) (d) (e)

(f) (g) (h) (i) (j)

Figure 7: Examples of (a)-(g) planes with good orientation estimates and (h)-(j) correctly classiﬁed non-planes.

vanishing points and images of rectangles, and gen-

eralises well to new data. Now that we have shown

this is possible, we intend to develop our algorithm to

automatically segment planar regions from images –

since we operate on whole regions as opposed to us-

ing local colour or edge information this will require

a different approach to standard image segmentation.

(a) (b) (c)

(d) (e) (f)

Figure 8: Where the method fails: (a),(b) show planes with

incorrect orientation estimate, whereas (c),(d) are false neg-

atives and (e),(f) are false positives for plane classiﬁcation.

ACKNOWLEDGEMENTS

This work was funded by UK EPSRC. With thanks to

Jos

e Mart

ınez-Carranza and Sion Hannuna for useful

discussions and advice.

REFERENCES

Bartoli, A. (2007). A random sampling strategy for piece-

wise planar scene segmentation. Computer Vision and

Image Understanding, 105(1).

Birchﬁeld, S. and Rangarajan, S. (2005). Spatiograms ver-

sus histograms for region-based tracking. In Com-

puter Vision and Pattern Recognitionn, volume 2.

Choi, S. (2008). Algorithms for orthogonal nonnegative

matrix factorization. In International Joint Confer-

ence on Neural Networks. IEEE.

Deerwester, S., Dumais, S., Furnas, G., Landauer, T., and

Harshman, R. (1990). Indexing by latent semantic

analysis. Journal of the American society for Infor-

mation Science, 41(6).

Fergus, R., Perona, P., and Zisserman, A. (2005). A sparse

object category model for efﬁcient learning and ex-

haustive recognition. In Computer Vision and Pattern

Recognition, volume 1.

Gee, A., Chekhlov, D., Calway, C., and Mayol-Cuevas, W.

(2008). Discovering higher level structure in visual

slam. Transactions on Robotics, 24.

Haines, O. and Calway, A. (2011). Estimating planar

structure in single images by learning from examples.

Technical Report CSTR-11-005, University of Bristol.

Hoiem, D., Efros, A., and Hebert, M. (2007). Recovering

surface layout from an image. International Journal

of Computer Vision, 75(1).

seck

a, J. and Zhang, W. (2005). Extraction, match-

ing, and pose recovery based on dominant rectangular

structures. Computer Vision and Image Understand-

ing, 100(3).

Lowe, D. (2004). Distinctive image features from scale-

invariant keypoints. International Journal of Com-

puter Vision.

Mart

ınez-Carranza, J. and Calway, A. (2010). Unifying pla-

nar and point mapping in monocular slam. In British

Machine Vision Conference.

Michels, J., Saxena, A., and Ng, A. (2005). High speed

obstacle avoidance using monocular vision and rein-

forcement learning. In International Conference on

Machine learning.

ık, B., Wildenauer, H., and Ko

seck

a, J. (2008). De-

tection and matching of rectilinear structures. In Com-

puter Vision and Pattern Recognition.

O Conaire, C., O’Connor, N. E., and Smeaton, A. F. (2007).

An improved spatiogram similarity measure for robust

object localisation. In International Conference on

Acoustics, Speech and Signal Processing, volume 1.

Rosten, E. and Drummond, T. (2006). Machine learning for

high-speed corner detection. Lecture Notes in Com-

puter Science, 3951.

Saxena, A., Sun, M., and Ng, A. (2008). Make3d: learning

3d scene structure from a single still image. Transac-

tions on Pattern Analysis and Machine Intelligence.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

294