A MEMETIC ALGORITHM FOR PROTEIN STRUCTURE
PREDICTION BASED ON THE 2D TRIANGULAR LATTICE
MODEL
Jyh-Jong Tsay and Shih-Chieh Su
Department of Computer Science and Information Engineering, National Chung Cheng University, Chiayi County, Taiwan
Keywords: Protein structure prediction, HP model, 2D triangular lattice model, Memetic algorithm.
Abstract: Proteins play fundamental and crucial roles in nearly all biological processes, such as, enzymatic catalysis,
signaling transduction, embryonic development, and DNA and RNA synthesis. The main function of the
protein is decided by its structure. Therefore, many researchers are interested in the prediction of protein
structure. The HP model is one of the commonly used models. But most research on the HP lattice model
focuses on how to solve the problem of optimization and ignores the purpose of protein structure prediction,
namely the prediction of structure similarity between proteins. The 2D triangular lattice model used in this
study can predicate protein structure more closely to its topology compared to the 2D square model
commonly used in the past. Besides proposing an effective memetic algorithm (MA), this study also
investigated structure similarity of natural proteins.
1 INTRODUCTION
The HP model (Lau and Dill, 1989) is a simplified
model which has become very popular
However, most researchers define the protein
folding or the protein structure prediction problems
as optimization problems. Therefore, these
researchers have favoured and focused research on
the 2D square or 3D cubic lattice model because
they have many associated benchmarks, large
amounts of data accumulated over the years, and the
availability of comparison with different strategies
and modeling methods. But what is ignored from
their studies is the main purpose of the protein
structure prediction: the similarity of protein
structures.
This study proposed a memetic algorithm (MA)
for protein structure prediction based on 2D
triangular lattice model. Our experimental results
show that the method developed in this study could
get lower free energy more effectively than previous
studies by other groups. This study further compared
the similarity of the Lattice Mode model and also
compared the result with the 3D face-centered-cubic
(FCC) lattice model for similarity. From the result of
numerical analysis, the 2D triangular lattice model
used in this study was shown to be better than the
3D FCC lattice on the prediction of the protein
structure with short sequences. This investigation
has not been probed into before by other researchers.
2 PRELIMINARIES
2.1 HP Model
In this model, each amino acid is classified based on
its hydrophobicity as either an H (hydrophobic or
non-polar) or a P (hydrophilic or polar). The HP
lattice model allows HP protein sequences to be
configured as self-avoiding walks (SAW) on the
lattice path favoring an energy free state due to HH
interaction. The energy of a given conformation is
defined as the number of topological neighboring
(TN) contacts between those Hs, which are not
adjacent in the sequence. Figure 1 shows an example
for the 2D triangular lattice model. The black filled
dots denote the hydrophobic amino acid and the red
open circles denote the hydrophilic amino acids. The
H-H contacts (free energy) in the conformation are
assigned the energy value of -1. The free energy is
defined as a minimum value; the maximum number
of H-H contacts is given in the case of two-
dimensional models. Figure 1 illustrates a protein
131
Tsay J. and Su S..
A MEMETIC ALGORITHM FOR PROTEIN STRUCTURE PREDICTION BASED ON THE 2D TRIANGULAR LATTICE MODEL.
DOI: 10.5220/0003710201310136
In Proceedings of the International Conference on Bioinformatics Models, Methods and Algorithms (BIOINFORMATICS-2012), pages 131-136
ISBN: 978-989-8425-90-4
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

structure with 15 H-H contacts (energy = -15). As a
result, the following problem can be formally
defined: given an HP sequence s = s
1,
s
2
...s
n ,
find a
correct number of matching pairs of the disulfide
bonds and energy-minimizing conformation of s;
that is: find c* ∈ C(s) such that E(c*) = min{E(c) | c
∈ C}, where C(s) is the set of all valid
conformations for s ( Shmygelska and Hoos, 2005).
Figure 1: An optimal conformation for the sequence
“(HP)
2
PH(HP)
2
(PH)
2
H P(PH)
2
” in a 2D triangular lattice
model.
2.2 2D Triangular Lattice Model
In the two-dimensional triangular lattice, each lattice
point has six neighbours. Since each residue has two
covalent neighbours except the first and the last
residues, a residue at a lattice point may be in
topological contact with at most four other residues.
Thus, each residue may be involved in at most 4 H-
H contacts (Joel et al., 2009). The unit vectors
shown in Figure 2 are logically defined. Real units
require normalization by
2
and are (1,0),(-1,0),
(-1/2,
3
/2),(1/2,-
3
/2),(1/2,
3
/2),(-1/2, -
3
/2).
After the unit vectors are obtained in the
triangular lattice, it is much easier to model protein
conformation on a two-dimensional triangular lattice
model without exhibiting the ‘parity’ problem
( Decatur and Batzoglou, 1996).
(x, y+1) (x+1, y+1)
(x-1, y)(x+1, y)
(x, y-1)
(x-1, y-1)
Figure 2: Neighbours of vertex (x, y). Each lattice point
has 6 neighbours.
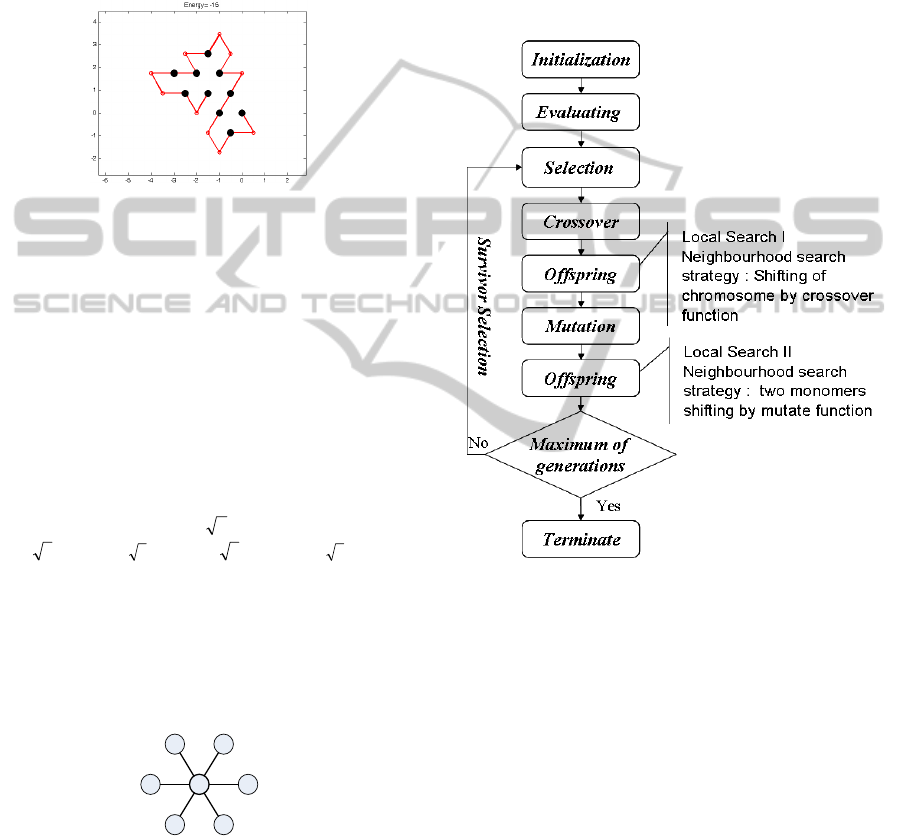
3 MEMETIC ALGORITHM
Memetic algorithms (MA) proposed by Moscato
(1999) are powerful algorithms. MA are a class of
stochastic global search heuristics in which
Evolutionary Algorithms-based approaches are
combined with local search techniques to improve
the quality of the solutions created by evolution
(Hart et al., 2005). In the PSP problem, a better
solution is to search for minimum free energy. The
details are illustrated in Figure 3. As the evolution
continues, the MA is expected to drive the search
toward the global optima.
Figure 3: Flowchart of the proposed MA.
This study proposes the use of a numerical
representation for chromosomes. In the PSP
problem, if the input amino acid sequence is of
length n, then each individual in the population is a
string of length n - 1 over the symbols {1,2,3,4,5,6},
which represent { L; LD; RD ; R; RU; LU }. The
symbols L; LD; RD ; R; RU; and LU are used to
denote the fold directions: L is for left, LD is for left-
down, RD is right-down, R is for right, RU is for
right-up and LU is for left-up in the genotype level
encoding scheme, respectively. In the phenotype
encoding scheme, coordinate (x,y) is used. {(-
1,0);(0,-1);(1,-1);(1,0);(0,1);(-1,1)}is in accordance
with the genotype level encoding scheme
{1,2,3,4,5,6}.
The following subsections describe the operators
of MA as in Figure 3.
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
132

3.1 Initialization
An initial population was generated randomly and
initialized an n - 1 dimensional space within a fixed
range. This study applied the method of the random
conformation generation by Depth-first search
(Hoque et al., 2010) to produce the initial population.
3.2 Evaluation
Each chromosome in the population needs to be
evaluated for its fitness. Here we directly used H-H
contacts of free energy as the fitness function. The
goal for an optimization algorithm like MA is to
minimize the fitness value, namely, free energy. The
evaluated chromosomes were sorted according to
their fitness values. This sorted population served as
the basis of subsequent reproduction process.
3.3 Selection
The selection operators include parent selection and
survivor selection. In this study, the tournament
selection method was used for this reproduction
process. Because of the repeatedly selecting, the best
individual of a randomly chosen subset is
tournament selection. The tournament size is
determined by choosing one out of two.
3.4 Crossover
Crossover combines the chromosomes from both
parents during the generation of offspring which will
inherit part of the genes from their parents. Bazzoli
and Tettamanzi (2004) tried a 3D-cube lattice model
on the three operators and their results show that 1-
point crossover performs better than the other two.
Therefore, 1-point crossover operators were used in
our study.
3.5 Local Search I
Local search is a method that searches and examines
iteratively the set of points in a neighborhood of the
current solution and replaces the current solution
with a better existing neighbour. In order to improve
the offspring, 1-point crossover operators were
further developed in our study and a new local
search was proposed.
The classical model was proposed by Unger and
Moult (1993) as a pivot rotation crossover operation
shown in Figure 4.
Figure 4: Rotation crossover operation (Unger and Moult
1993). (a) And (b) are parents, (c) is offspring. ‘’
indicates crossover positions. (a) is the first half of
chromosome1. (b) is the latter half of chromosome2. (a)
and (b) combination becomes (c) and is also the best
structure.
However, our study found that the rotation
crossover operation could not fit into some situations,
for example, Figure 5. The use of a shift crossover
operation might get a better outcome if some kind of
structure existed.
Figure 5: Shift crossover operation. (a) is the first half of
chromosome1. (b) is the latter half of chromosome2. (c) is
the best structure. In this case (a) and (b) can’t combine by
using the method of rotation. On the contrary, it can get
the best structure by using the method of shift.
Therefore, this study proposes a new
neighbourhood search strategy. It contains the
crossover operation of Rotation and Shift as shown
in Figure 6.
Figure 6: Neighbourhood search strategy. ‘’ indicates
crossover positions. The offspring (d) is the first half of
(a). The offspring (e) is the first half of (b). We rotate (e)
to (e’) and combine (d) by shift. Then we can get the best
solution (f).
A MEMETIC ALGORITHM FOR PROTEIN STRUCTURE PREDICTION BASED ON THE 2D TRIANGULAR
LATTICE MODEL
133

In Figure 6, it is found that the best solution can
not be obtained by using the Rotation or Shift (the
arrowhead pointing to crossover positions). If (e) is
rotated to (e’) before doing the operation of Shift,
the best solution can be achieved.
3.6 Mutation and Local Search II
Mutations can lead GA into genetic structures that
have never been searched before. Common mutation
operators are bit-flip mutations; however, mutation
operators without previous design will lead to
invalid conformation.
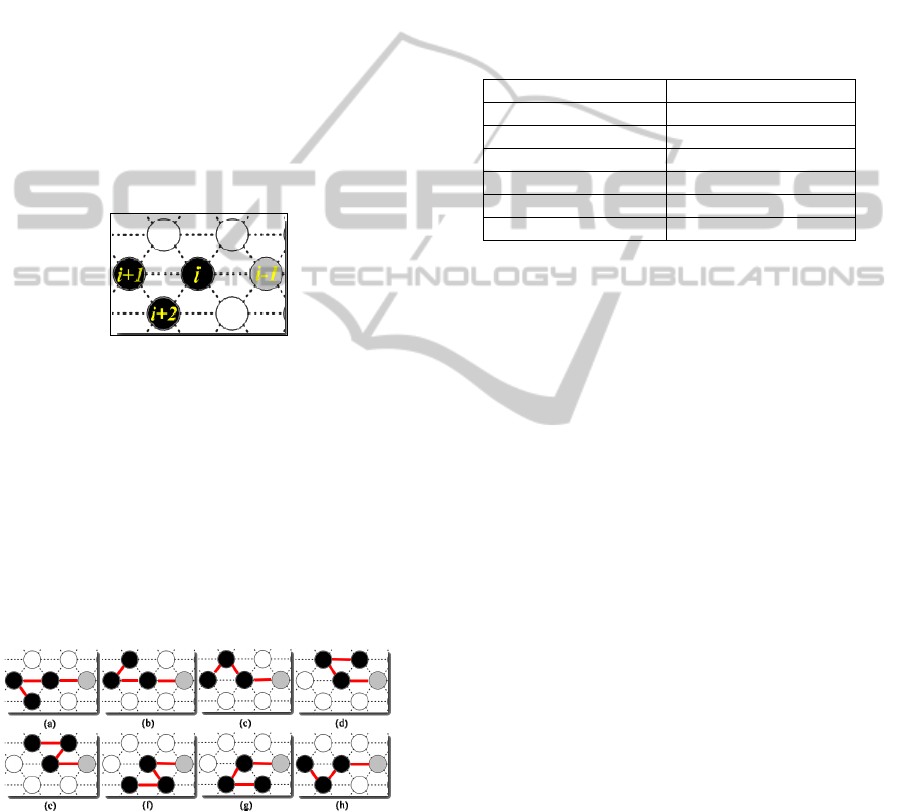
It is found from our study that two monomers
could form a contact only at the bond angle of 60
0
in
the 2D triangular lattice model. Based on this
feature, a new local search was proposed in our
study as illustrated in Figure 7.
Figure 7: Mutation operators. The i is mutation point. The
i is mutation point ,i-1 is the former gene, i+1 and i+2 are
the actual changed genes.
When the mutation operators are in process, one
mutation point will be chosen randomly while
neighbourhood function uses the information from
mutation point genes to mutate in a regular pattern
on the following two genes followed by evaluating
the chromosomes in the offspring set as shown in
Figure 8. The best chromosome will be retained to
replace the original one.
Figure 8: Neighbourhood search strategy. When the
mutation operators are proceeding it is found from our
study that two monomers could form a contact only at the
bond angle of 60
0
in the 2D triangular lattice model.
3.7 Termination
This generational process is repeated until a
termination condition has been reached. The
termination condition of the study is to adopt the
fixed number of generations reached. Finally, the
best member of the population is then returned.
3.8 Parameter Settings
The main purpose of the study was to compare the
methods. Better results could be obtained if the
population size was set larger. Due to limitation on
experimental time, the experiment of this part is
parameter settings as shown in Table 1.
Table 1: Parameter settings.
Operations/Parameters Setting
Population size 100
Crossover rate 0.8
Mutation rate 0.4
Parents selection Tournament selection
Survival selection μ+λ
Termination 200 generations
4 EXPERIMENTAL RESULTS
In order to validate the result of the study, the
experiment was divided into two stages.
4.1 General Benchmark
In the past, a few researchers used the 2D Triangular
Lattice Model to proceed for the Protein Structure
prediction. This study also added three groups of
longer sequence. Sequences 1 through 4 used in this
study were described in Krasnogor et al., (Krasnogor
et al. 2002); Sequence 5-7 was taken from Jiang et
al., (2003) and the last three instances were from
(Shmygelska and Hoons, 2005). These sequences
have been used as the benchmark for the 2D square
HP model as shown in Table 2.
This study in comparison with previous studies
provided a means of demonstrating the effectiveness
of the method described here. The multimeme
algorithm (MMA) is the method that Krasnogor et
al., (Krasnogor et al., 2002) proposed. The hybrid
genetic algorithm (HGA) is the method that Hoque
et al., (Hoque et al., 2006) proposed. Further, the
hill-climbing and genetic algorithm is the method
that this study
(Su et al., 2010) proposed previously.
Comparing this current method with the method
mentioned above, it can be concluded from Table 3
that MA performed more robustly than others.
Table 3 shows the results of 10 sequences after
20 rounds of operations being performed. The
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
134

format of column entries is ‘average / minimum’.
Figures in bold indicate the lowest energy.
Table 2: The benchmarks for the 2D triangular lattice HP
model.
# Len. Protein Sequence
1 24 HHPPHPPHPPHPPHPPHPPHPPHH
2 30a HHHPPHPPHPPHPPHPHPPHPHPPHPPHHH
3 30b HHHPPHPPHPPHPHPPHPHPPHPPHPPHHH
4 37
HHHPPHPPHPPHPHPHPPHPPHPPHPPPPPH
PHPHHH
5 50 H
2
(PH)
3
PH
4
PH(P
3
H)
2
P
4
(HP
3
)
2
HPH
4
(PH)
3
PH
2
6 60 P(PH
3
)
2
H
5
P
3
H
10
PHP
3
H
12
P
4
H
6
PH
2
PHP
7 64 H
12
(PH)
2
((P
2
H
2
)
2
P
2
H)
3
(PH)
2
H
11
8 85 H
4
P
4
H
12
P
6
(H
12
P
3
)
3
HP
2
(H
2
P
2
)
2
HPH
9 100a
P
3
H
2
P
2
H
4
P
2
H
3
(PH
2
)
2
PH
4
P
8
H
6
P
2
H
6
P
9
HPH
2
PH
11
P
2
H
3
PH
2
PHP
2
HPH
3
P
6
H
3
10 100b
P
6
HPH
2
P
5
H
3
PH
5
PH
2
P
4
H
2
P
2
H
2
PH
5
PH
10
PH
2
PH
7
P
11
H
7
P
2
HPH
3
P
6
HPH
2
Table 3: Comparison of the proposed approach with the
HHGA (Su et al., 2010 ), MMA (Krasnogor et al., 2002 ),
HGA(Hoque et al., 2006) and TS (Böckenhauer et al.,
2008). Figures in bold indicate the lowest energy. MA was
run for 200 iterations with the population size 100. For
sequence 6, 200 iterations with population size 400.
# Len. MA HHGA MMA HGA TS
1 24 -15.6/-17 - /-16 - /-17
2 30a -21.65/-24 - /-24 - /-25
3 30b -22.35/-24 - /-24 - /-25
4 37 -25.73/-28 - /-26 - /-29
5 50 -36.2/-38 -33.15/-35 - /-23
6 60 -67.65/-70 -60.5/-65 - /-46 - /-70
7 64 -61.05/-68 -53.5/-56 - /-46 - /-50
8 85 -88.95/-93 -81.2/-86
9 100a -80.65/-85 -71.55/-79
10 100b -79.6/-83 -71.6/-77
4.2 PDB Benchmark
In this study, the benchmarks are the small proteins.
The benchmarks in this study are listed in Table 4.
The small protein data were collected from the
protein data bank (PDB) (http://www.rcsb.org/pdb/).
In this study, the LatPack Tools – LatFit (Mann
et al., 2008) were firstly used to get the best
conformation of the 3D FCC lattice model. Then,
MA was applied to find the best conformation of the
2D Triangular lattice model and PyMOL followed to
proceed to compare structures in order to get the
value of RMSD. To compare with the 3D FCC
lattice model, this study used the CPSP-web-tools
(Mann et al., 2008; 2009) to get the best
conformation in the 3D FCC lattice model and also
used PyMOL ( http://www.pymol.org/
) to compare
this conformation with benchmark proceeding
structure to get the value of RMSD. Based on the
value of RMSD, the similarity from different lattice
models can be compared objectively. From
experimental results, the best conformation of the
2D Triangular lattice model is better than the best
conformation of the 3D FCC lattice model in the
structure similarity. Table 5 summarizes the result.
Table 4: Benchmarks from PDB.
#
PDB
ID
Len. Protein Sequence
1 1CNL 12 GCCSDPRCAWRC
2 1A0M 16 GCCSDPRCNMNNPDYC
3 1V6R 21 CSCSSLMDKECVYFCHLDIIW
4 1CZ6 25 RSVCRQIKICRRRGGCYYKCTNRPY
5 1EI0 38
DPCQKQAAEIQKCLQANSYLESKC
QAVIQELKKCAAQY
6 1CRN 46
TTCCPSIVARSNFNVCRLPGTPEAIC
ATYTGCIIIPGATCPGDYAN
71EHS 48
STQSNKKDLCEHYRQIAKESCKKGF
LGVRDGTAGACFGAQIMVAAKGC
81E8R 50
MGNQQCNWYGTLYPLCVTTTNGW
GWEDQRSCIARSTCAAQPAPFGIVGSG
9 1IL8 72
SAKELRCQCIKTYSKPFHPKFIKELR
VIESGPHCANTEIIVKLSDGRELCLD
PKENWVQRVVEKFLKRAENS
Table 5: RMSD: comparison of the proposed approach
with the CPSP-Tools 3D FCC lattice model.
# PDB ID Length
MA based
on 2D
Triangular
CPSP
based on 3D
FCC
1 1CNL 12
1.017
1.203
2 1A0M 16
1.497
1.518
3 1V6R 21
1.661
2.437
4 1CZ6 25
3.040
3.377
5 1EI0 38
3.187
3.429
6 1CRN 46
3.012
3.533
7 1EHS 48
2.828
3.673
8 1E8R 50
3.218
4.225
9 1IL8 72
3.731
4.158
5 CONCLUSIONS
In the ab initio technique, the lattice model is one of
the most frequently used methods in protein
structure prediction.
A MEMETIC ALGORITHM FOR PROTEIN STRUCTURE PREDICTION BASED ON THE 2D TRIANGULAR
LATTICE MODEL
135

Some researchers can improve 2D triangular and
3D FCC lattice models to reach 16/30 (53%)
(Decatur and Batzoglou, 1996) and 31/36 (86%)
(Hart and Istrail, 1997) of approximation ratios and
can even achieve a higher structure similarity.
However, most researchers define the protein fold
problem or the protein structure prediction problem
as an optimization problem. Therefore, most of the
studies usually use the lower approximation ratios of
lattice model, such as the 2D square and 3D cube
lattice models.
This study proposed a memetic algorithm (MA)
for protein structure prediction based on the 2D
triangular lattice model. The result from our
experiments showed that the method could get lower
free energy in a more effective way than previous
studies. In addition, this study further compared the
structure similarity of the lattice mode and also
compared the result from the 3D FCC lattice model
for the structure similarity. From the result of
numerical analysis, the 2D triangular lattice model
used in this study was better than the 3D FCC lattice
on the prediction of the protein structure with short
sequences. This means that the 2D triangular lattice
model can get more similar simulating results with
the HP Lattices Model to predict the protein
structure with short sequences. In conclusion, the
2D triangular lattice model is a better choice than the
previous approaches. This is the first time that this
method has been investigated and its further study in
the future will be worthwhile.
REFERENCES
Bazzoli, A., and Tettamanzi, A.G.B. , A Memetic
Algorithm for Protein Structure Prediction in a 3D-
Lattice HP Model, Evo Workshops 2004, LNCS 3005,
2004, pp. 1–10.
Böckenhauer, H-J., Ullah, A. D., Kapsokalivas, L., and
Steinhöfel, K. , A Local Move Set for Protein Folding
in Triangular Lattice Models, Algorithms in
Bioinformatics, LNCS, 2008, pp. 369-381.
Decatur, S. and Batzoglou, S., Protein folding in the
Hydrophobic-Polar model on the 3D triangular lattice,
In 6th Annual MIT Laboratory for Computer Science
Student Workshop on Computing Technologies, 1996.
Hart, W. E., Krasnogor, N., and Smith, J. E., Memetic
Evolutionary Algorithms, Studies in Fuzziness and
Soft Computing, 2005, Volume 166.
Hart, W.E., and Istrail, S., Lattice and Off-Lattice Side
Chain Models of Protein Folding: Linear Time
Structure Prediction Better than 86% of Optimal,
Journal of Computational Biology, 1997, pp.241–259.
Hoque, M., Chetty, M., Lewis, A., Sattar, A., and Averya,
V. M., DFS-generated pathways in GA crossover for
protein structure prediction, Pattern Recognition in
Bioinformatics, 2010 , pp. 2308-2316.
Hoque, M. T., Chetty, M., and Dooley, L. S., A hybrid
genetic algorithm for 2D FCC hydrophobic–
hydrophilic lattice model to predict protein folding, in:
Proceedings of the 19th ACS Australian Joint
Conference on Artificial Intelligence, LNAI, Springer,
2006, pp. 867–876.
Jiang, T., Cui, Q., Shi, G., and Ma, S., Protein folding
simulations for the hydrophobic-hydrophilic model by
combining tabu search with genetic algorithms ,
Journal of Chemical Physics, 2003, pp.4592-4596.
Joel, G., Martin, M., and Minghui, J., RNA folding on the
3D triangular lattice, BMC Bioinformatics, 2009,
doi:10.1186/1471-2105-10-369.
Krasnogor, N., Blackburne, B. P., Burke, E. K., Hirst, J.
D., Multimeme algorithms for protein structure
prediction, PPSN VII, LNCS2439 , 2002, pp. 769–778.
Lau, K. F., and Dill, K. A., lattice statistical mechanics
model of the conformation and sequence space of
proteins, Macromolecules, 1989, pp. 3986-3997.
Mann, M., Smith, C., Rabbath, M., Edwards, M., Will, S.,
and Backofen, R., CPSP-web-tools: a server for 3D
lattice protein studies. Bioinformatics, 2009, pp.676-
677.
Mann, M., Will, S., and Backofen, R., CPSP-tools - Exact
and Complete Algorithms for High-throughput 3D
Lattice Protein Studies, In BMC Bioinformatics, 2008,
pp.230.
Mann, M., Maticzka, D., Saunders, R., and Backofen, R.,
Classifying protein-like sequences in arbitrary lattice
protein models using LatPack. In HFSP Journal,
2008, pp.396.
Moscato, P., On evolution, search, optimization, genetic
algorithms and martial arts: Towards memetic
algorithms, Technical Report Caltech Concurrent
Computation Program Report 826, California ,1989.
Shmygelska, A., and Hoos, H. H., An ant colony
optimisation algorithm for the 2D and 3D hydrophobic
polar protein folding problem, BMC Bioinformatics,
2005, pp. 30
Su, S-C., Lin, C-J, and Ting, C-K, An efficient hybrid of
hill-climbing and genetic algorithm for 2D triangular
protein structure prediction, IEEE International
Conference on Bioinformatics and Biomedicine
Workshops (BIBMW), 2010, pp.51-56.
Unger, R., and Moult, J., Genetic algorithms for protein
folding simulations, Journal of Molecular Biology ,
1993, pp. 75–81.
BIOINFORMATICS 2012 - International Conference on Bioinformatics Models, Methods and Algorithms
136