
MULTIPLE TARGET TRACKING AND IDENTITY LINKING
UNDER SPLIT, MERGE AND OCCLUSION OF TARGETS AND
OBSERVATIONS
Jos
´
e C. Rubio, Joan Serrat and Antonio M. L
´
opez
Computer Vision Center and Comp. Science Dept., Universitat Aut
`
onoma de Barcelona, 08193 Cerdanyola, Spain
Keywords:
Tracking, Graphical models, MAP inference, Particle tracking, Live cell tracking, Intelligent headlights.
Abstract:
Multiple object tracking in video sequences is a difficult problem when one has to simultaneously deal with
the following realistic conditions: 1) all or most objects share an identical or very similar appearance, 2)
objects are imaged at close positions so there is a data association problem which becomes worse when the
number of targets is high, 3) the objects to be tracked may lack observations for a short or long interval, for
instance because they are not well detected or are being temporally occluded by another non-target object, and
4) their observations may overlap in the images because the objects are very near or the image results from a
2D projection from the 3D scene, giving rise to the merging and subsequently splitting of tracks. This later
condition poses the additional problem of maintaining the objects identity when their observations undergo
a merge and split. We pose the tracking and identity linking problem as one of inference on a two-layer
probabilistic graphical model and show how can it be efficiently solved. Results are assessed on three very
different types of video sequences, showing a turbulent flow of particles, bacteria growth and on-coming traffic
headlights.
1 INTRODUCTION
In the context of multiple target detection and tracking
the following definitions will help us to state the goal.
A target or object is some real moving entity, imaged
in a video sequence, that we want to follow in order to
analyze its motion for some purpose (like people and
vehicles for surveillance (Benfold and Reid, 2011),
particles in a turbulent flow for its characterization,
live micro-organisms for lineage studies (Liu et al.,
2009), (Li et al., 2007), or insects for behaviour stud-
ies (Laet et al., 2011). An observation or measure-
ment is the detection of an object as it appears in an
image. Note that a single observation can actually re-
sult from several objects whose observations overlap.
Data association is the process of relating objects
to observations. In the absence of merges/splits, each
target corresponds to a unique observation, and there-
fore targets are unambiguously identified as long as
the track construction is correct. In presence of oc-
clusions, mapping targets and observations is a dif-
ficult problem to solve. Moreover, tracking multiple
objects implies multiple object interactions and map-
ping between observations, which is costly to solve
optimally.
There are many works on visual multiple target
tracking. Only some of them try to maintain iden-
tities in addition to build tracks and, being the most
interesting type of result, we will focus on them in
the following review. The usual classification of past
works we have found is according to the strategy or
the techniques employed for data association, that is,
whether they are based on multiple hypothesis track-
ing (MHT) (Reid, 1979), joint probabilistic density
association (JPDA) (T.Fortmann et al., 1983), particle
filtering (Khan et al., 2003), integer linear program-
ming, graph algorithms (like min-cut and set cover),
inference on Bayesian networks (Nillius et al., 2006),
etc. Being MHT and JPDA the most widely used ap-
proaches, they present some drawbacks. As MHT
suffers from state space explosion when applied to
real videos, JPDA assumes a fixed number of targets,
and only considers measurements in the current frame
step.
Another relevant categorization criterion is
whether the tracking is batch (Zheng Wu and Betke,
2011), (Nillius et al., 2006) or online (Benfold
and Reid, 2011), that is, tracks (and identities) are
resolved once the whole sequence is available or it
is done as each frame is ready. Clearly, the batch
strategy has the advantage of working with all the
data along time and it makes sense to use it in
problems which do not require an online answer like
live cell tracking or turbulent flow analysis. However,
15
Rubio J., Serrat J. and López A. (2012).
MULTIPLE TARGET TRACKING AND IDENTITY LINKING UNDER SPLIT, MERGE AND OCCLUSION OF TARGETS AND OBSERVATIONS.
In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 15-24
DOI: 10.5220/0003710600150024
Copyright
c
SciTePress
in other applications a fast answer is needed to make
a decision, like in surveillance or headlights control
(Rubio and Serrat., 2010).
We believe that a better understanding of the state
of the art can be grasped on the basis of the actual
multiple target tracking problem being solved in each
case. We mean that by just slightly changing the way
the targets or the observations are assumed to evolve
along time, or the (often implicit) relationships be-
tween a target and its observation (how may it appear
in the image), one gets a very different problem to
solve. This in turn determines the kind of methods
to use. Just as an example, if targets are perfectly
segmented (no false positives or negatives, each tar-
get gives rise to exactly one observation and to each
observation corresponds one target) we have a purely
problem of data one-to-one association which can be
solved by the Hungarian method (Kuhn, 1955). How-
ever, if one target may be over-segmented into several
regions and we want to be aware of it, the problem is
quite different.
The different tracking scenarios can vary from the
simplest case (one target is one measure, and one
measure is one target), to more complicated situa-
tions. In the most general case, a target can produce
0,1, or more measurements, and one measurement can
be produced by 0, 1 or many targets. Table 1 presents
different scenarios regarding the evolution of targets
in time. In order to unequivocally define our track-
ing application, we analyze both the behavior of our
targets in time and its relationships with the image
measurements. Table 2 presents these relationships
for the different sequences we provide in the experi-
ments: Synthetic flow in FIg. 1, Vehicle headlights in
Fig 2 and Bacteria growht in Fig. 3.
Instead of designing a tracking method for a spe-
cific instance of a problem, our goal is to provide
a generic multiple target tracking algorithm that can
handle as many of those situations within a unique
framework.
1.1 Overview of the Approach
We propose a two-component algorithm that outputs
the complete trajectories of each of the targets in a
video sequence. The first component handles the cre-
ation of tracklets within a local window of frames,
and the other performs tracklet linking and data as-
sociation. The Tracklet Creation is based on examin-
ing a window of a few frames, and establishing corre-
spondences between the observations in each of these
images. We define a tracklet as an ordered list of ob-
servations of the same target, between frames j and
l, generated by a series of one-to-one associations be-
Table 1: The five possible scenarios regarding the evolution
of a track along time.
Targets
t t + 1
(1). New targets may appear 0 1
(2). Targets can disappear 1 0
(3). Regular case 1 1
(4). A target can become n
(e.g cell mitosis)
1 n
(5). m targets can become
one (e.g cell fusion)
m 1
Table 2: Definition of our application tracking problem. Re-
lationship target-observation, combined with the evolution
in time of the targets.
Target Scenario Targets Obs.
Synthetic Flow (1),(2),(3)
1 1
n 1
Headlights (1),(2),(3),(4)
1 0
1 1
1 n
m 1
Bacteria (3),(4) 1 1
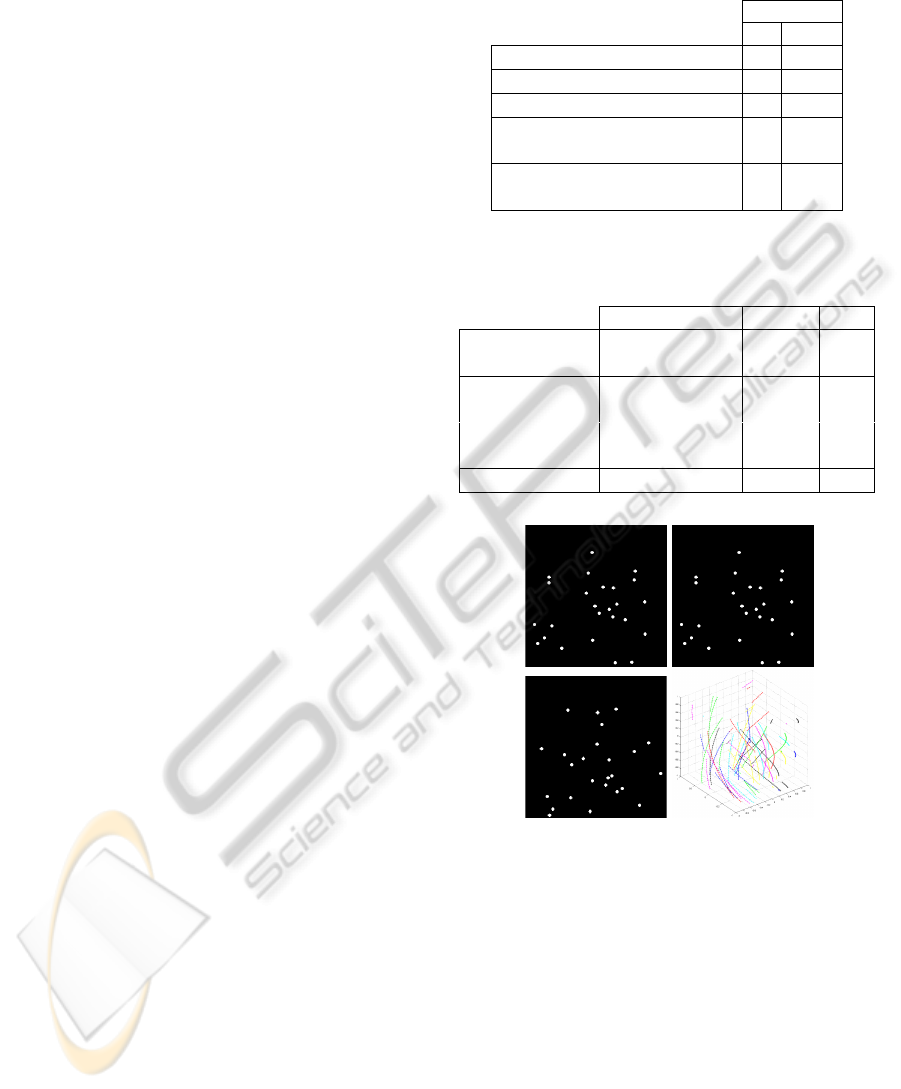
Figure 1: Sample frames of particles in a synthetic helical
flow and flow lines. Each particle is always seen as a blob
and one blob corresponds to one or several particles, if they
overlap. Blobs merge and split but don’t get occluded by
other things.
tween observations in consecutive frames.
This work is focused on tracking multiple targets
which seldom produce any appearance information,
or such information is useless because every target
looks the same (See Figures 1-3, for samples of the
applications’ frames). This is an important handicap
when addressing a problem of data association. We
overcome this disadvantage by exploiting instead, the
target’s motion information, as well as assuming cer-
tain rigidity on the movement of the targets between
contiguous frames. Graph Matching provides a per-
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
16

Figure 2: Successive frames from a night driving video se-
quence recorded by an on-board camera. One blob may cor-
respond to two far away light sources or reflections. Blobs
merge, split and get occluded by other vehicles, trees and
fences.
Figure 3: Sample frames of the bacteria growth video se-
quence. Every bacterium will be correctly segmented and
to each region will correspond a single bacterium (perfect
detection and no overlapping). Some bacteria divide (splits)
while others just grow.
fect tool to encode this knowledge. We can see each
of the frames as a graph, were every observation cor-
responds to a node in the graph, and it is represented
by its centroid position in the image. To create the
set of tracklets for a certain window of frames, we
perform matching of these graph representations be-
tween every pair of consecutive frames in the window.
The Track Idenity Linking step has two main
goals. First, finding the identity of the target of
those observations presenting uncertainty or ambigu-
ity about the identity of its corresponding target (data
association). Second, linking tracklets of different
windows which belong to the same target. We simul-
taneously solve these two problems by modeling the
tracklet identity ambiguities in what we call an Hy-
pothesis Graph, and then inferring the most likely hy-
pothesis of track-target correspondences.
2 CONSTRUCTION OF LOCAL
TRACKLETS
We present a probabilistic-based graph matching ap-
proach to construct target tracklets in a window of
frames. Let w be the number of frames in a certain
temporal window of the video sequence. We denote
by I
1
, I
2
, ...I
w
the different frames within this window.
Each frame contains a set of zero or more observa-
tions, indexed by p, q,... . An association a is an or-
dered pair of observations from the same target, but at
different frames. Let A be the set of all such associa-
tions,
A = {a = (p, q)|p ∈ I
i
, q ∈ I
j
, 1 ≤ i < j ≤ w}, (1)
where a, b, ... index the elements of A, so that we
can denote all pairs of association without repeated
combinations as (a, b), a < b. Let X = (...X
a
...) be
the vector of binary variables, one per association,
where X
a
= 1 if the corresponding association a ex-
ists, and zero otherwise. In the same way, the vec-
tor of all measurements is denoted by Y = (...Y
a
...),
where each association a = (p, q) is represented by
Y
a
= [p
x
, p
y
, q
x
, q
y
]. Thus, each association is at-
tributed with the spatial coordinates of its origin and
destination points. Although, other properties may
be also considered, like size, shape, or intensity mea-
sures.
Our goal is to find the most likely configuration
of the set X of association states, given the set of all
measurements Y. This is, to find the maximum a pos-
teriori estimation,
X
∗
= argmax
X
p(X|Y). (2)
In a Bayesian framework, the posterior probability
of the hidden variables X, given the measurements, is
proportional to the product of the likelihood and prior
terms
p(X|Y) ∝ p(Y|X)p(X). (3)
The likelihood term p(Y|X) encodes the obser-
vation model. The prior p(X) encodes certain con-
straints on the generation of tracklets. The next two
sections detail how do we define and compute these
two terms.
2.1 Observation Model
To build a generic observation model, we start by enu-
merating the set of premises that every Multiple Tar-
get Tracking scenario should satisfy:
• Measurements belonging to the same track can
not move too far between consecutive frames.
MULTIPLE TARGET TRACKING AND IDENTITY LINKING UNDER SPLIT, MERGE AND OCCLUSION OF
TARGETS AND OBSERVATIONS
17
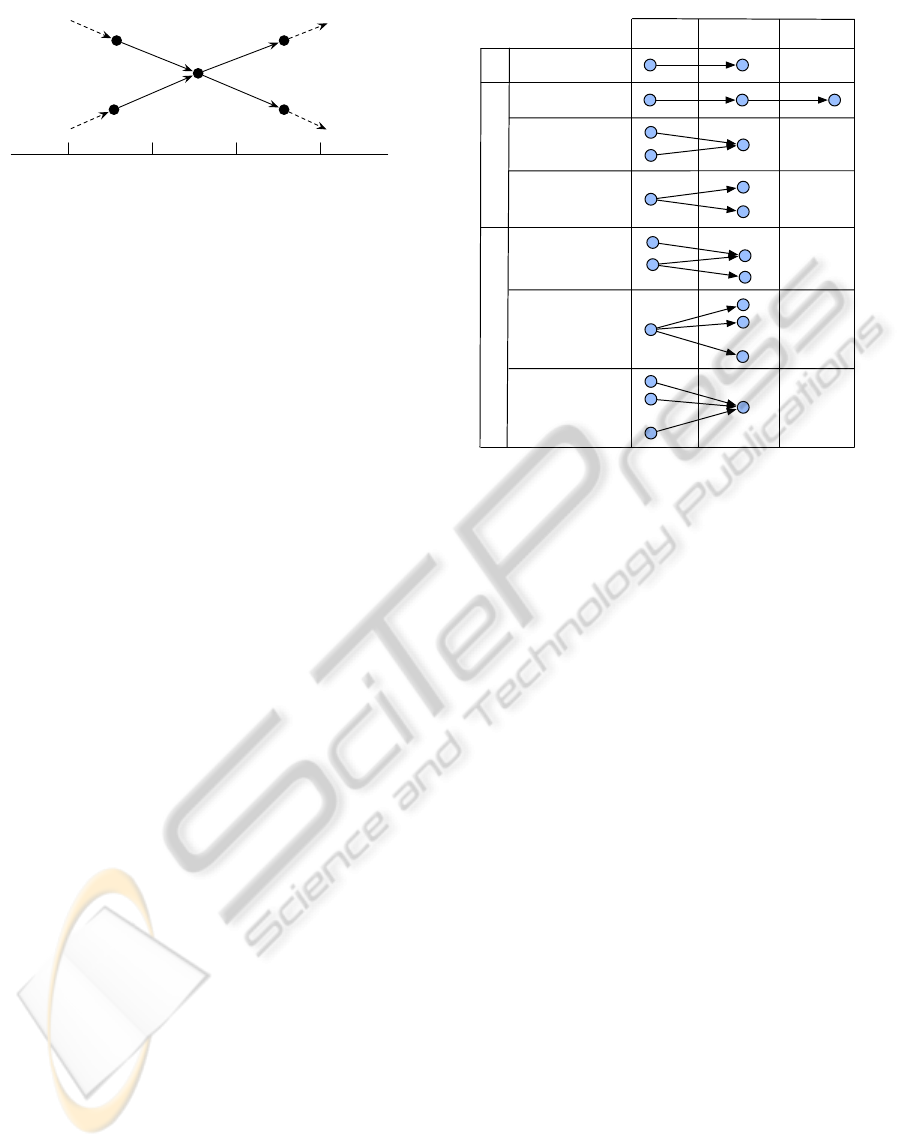
p
q
vpq
r
vqr
s
t
vsq
vqt
I1 I2 I3 I4 I5
Figure 4: Target motion vectors involved in a two targets
merging and splitting.
• Targets follow fairly smooth trajectories with con-
stant speed between consecutive frames.
• Close targets in colliding directions are likely to
merge.
• A target entrance and departure strongly depends
on its location in the image.
We encode the first three assumptions in the fol-
lowing likelihood factorization. The fourth constraint
will be modeled in the data association step, as we
will explain later.
p(Y|X) =
∏
a∈A
p
A
(Y
a
|X
a
) ·
∏
(a,b)∈N
p
N
(Y
a
,Y
b
|X
a
, X
b
)
The first term models the likelihood of an asso-
ciation being active or inactive, depending on the lo-
cation of the two features (p, q) involved in each as-
sociation a ∈ A. The second term, defined over the
set N of pairs of associations, is the likelihood of two
associations existing simultaneously. This pairwise
terms smooths the object motion (speed and direction)
along several frames, and also models the likelihood
of merging and splitting events. See Figure 5.
Following we present the probabilistic modeling
of each of the likelihood terms based on the previ-
ously stated assumptions.
Displacement. The likelihood of a single associa-
tion is defined as:
p
A
(Y
a
|X
a
) = N (|v
pq
|, µ
A
, σ
A
), (4)
where N is as a Normal distribution, defined on the
norm of the vector v
pq
, or the target velocity.In order
to define our observation model as generic as possi-
ble we do not establish any correlation between the
movement of a target and its appearance or image po-
sition. Although in the context of a specific applica-
tion it would be convenient to apply constraints more
complex and discriminative.
The pairwise term of the likelihood is, in turn, fac-
torized in three different terms: p
L
, p
M
and p
S
. The
first penalizes sudden changes on speed and direction,
and the other two model the likelihood of two targets
merging and splitting.
Ij Ik Il
...
...
regular associations
direction-speed
mergings
splittings
disjoint merging-
splitting
num. splitting
features ≤ n
num. merging
features ≤ m
constraints
A
N
Figure 5: Sets of associations involved in the likelihood (A,
N) and prior (constraints).
Linear Trajectories and Speed. The set of pairs of
associations related to the trajectory of the tracks is
defined as
N
L
= {(a, b) ∈ N|a = (p, q), b = (q, r)}. (5)
and its pairwise likelihood is defined as a mixture of
densities,
p
L
(Y
a
,Y
b
|X
a
, X
b
) = αN (
\
v
pq
v
qr
, µ
dir
, σ
dir
) (6)
+ (1 − α)N (|v
pq
| − |v
qr
|, µ
vel
, σ
vel
).
where the parameter α ∈ [0, 1] weights the contribu-
tion of each component. The first Normal distribution
models inter-frame target direction changes in terms
of angles between consecutive motion vectors. The
second density encodes the changes in target velocity,
which are expected to be near zero, always between
consecutive frames. Figure 4 shows a simple example
of target motion vectors.
Merging & Splitting. The following densities
model the probability of two features merging, or one
feature splitting in two. Their respective sets of pairs
of associations are:
N
M
={(a, b) ∈ N|a = (p, q), b = (s, q)}. (7)
N
S
={(a, b) ∈ N|a = (q,t), b = (q, r)}.
Their pairwise densities define a correlation on the
direction and distance between merging or splitting
features. In this case, no assumptions can be made
about the data following a Gaussian distribution. In-
stead, we use a Kernel Density Estimator to model the
functions
ˆ
f
M
, and
ˆ
f
S
from training data.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
18

p
M
(Y
a
,Y
b
|X
a
, X
b
) =
ˆ
f
M
(
\
v
pq
v
sq
, |
−→
ps|) (8)
p
S
(Y
a
,Y
b
|X
a
, X
b
) =
ˆ
f
S
(
\
v
qt
v
qr
, |
−→
tr |) (9)
2.2 Hard Constraints
We include a constraint on the maximum number of
features to which one feature can be associated. This
may be used in tracking applications for which we
know the bounds on the number of features involved
in splits and merges. Given two frames I
i
, I
j
, from a
window of length w, we define what we call the multi-
assignment m-to-n constraint as
∑
a∈A(p)
X
a
≤ m, ∀p ∈ I
i
, i = 1. . . w − 1 (10)
∑
b∈B(q)
X
b
≤ n, ∀q ∈ I
j
, j = 2. . . w, (11)
where A(p) is the set of associations leaving feature
p ∈ I
i
and B(q) the set of those arriving at q ∈ I
j
.
Split and merge handling gives rise to an addi-
tional constraint to avoid bizarre tracklet configura-
tions, like a merge mixing with a split and vice versa.
See Figure 5 (disjoint merging-splitting). This takes
the form
X
a
+ X
b
+ X
c
≤ 2, (12)
where a, b, c are the three associations involved in the
joint merging-splitting.
Note that all the constraints of Eqs. (10) - (12)
have the form of an upper bound on a linear combi-
nation of a few association variables. Thus, if r is the
number of constraints, all of them can be compactly
expressed as CX
T
≤ b, where C = [c
1
, c
2
, ..., c
r
]
T
is a
very sparse binary matrix whose rows select the vari-
ables of each constraint, and b is a column vector with
bounds m, n, and 2. Then, the prior reduces to
P(X = x) =
1 if Cx ≤ b
0 otherwise
(13)
3 ONLINE DATA ASSOCIATION
In the following section we introduce the second ma-
jor contribution of this work, consisting of a prob-
abilistic method to adress the data association prob-
lem. Given a set of tracklets generated in the previous
step, the goal is to find the most probable one-to-one
correspondences between tracklets and track identi-
ties. Some of the tracklet identities can be unambigu-
ously determined if they do not interact with any other
tracklet along their lifetime. Unfortunately, in a con-
text with a great amount of targets it is less likely to
find tracklets which do not interfere with each other.
Lets assume that a set of tracklets {t
1
,t
2
, ..., t
n
} is
constructed up to frame s. Each tracklet is, in turn, a
list of contiguous observations between two frames.
In the present context, an observation or measure-
ment is defined simply by the feature centroid in im-
age coordinates, as o
a
∈ O. Thus, a tracklet a be-
tween two arbitrary frames I
i
,I
k
, is formally denoted
as t
i:k
a
= {o
i
a
, o
i+1
a
, ..., o
k
a
}, being i < k ≤ s. However,
the measurements used to find the target identities are
mainly related with the movement of the targets. We
say that M
k
a
= o
k
a
− o
k−1
a
is the motion vector of the
observation o
a
∈ I
k
.
Following, we formally define the Hypothesis
Graph, and introduce a probabilistic method to obtain
the most likely hypothesis of track labels.
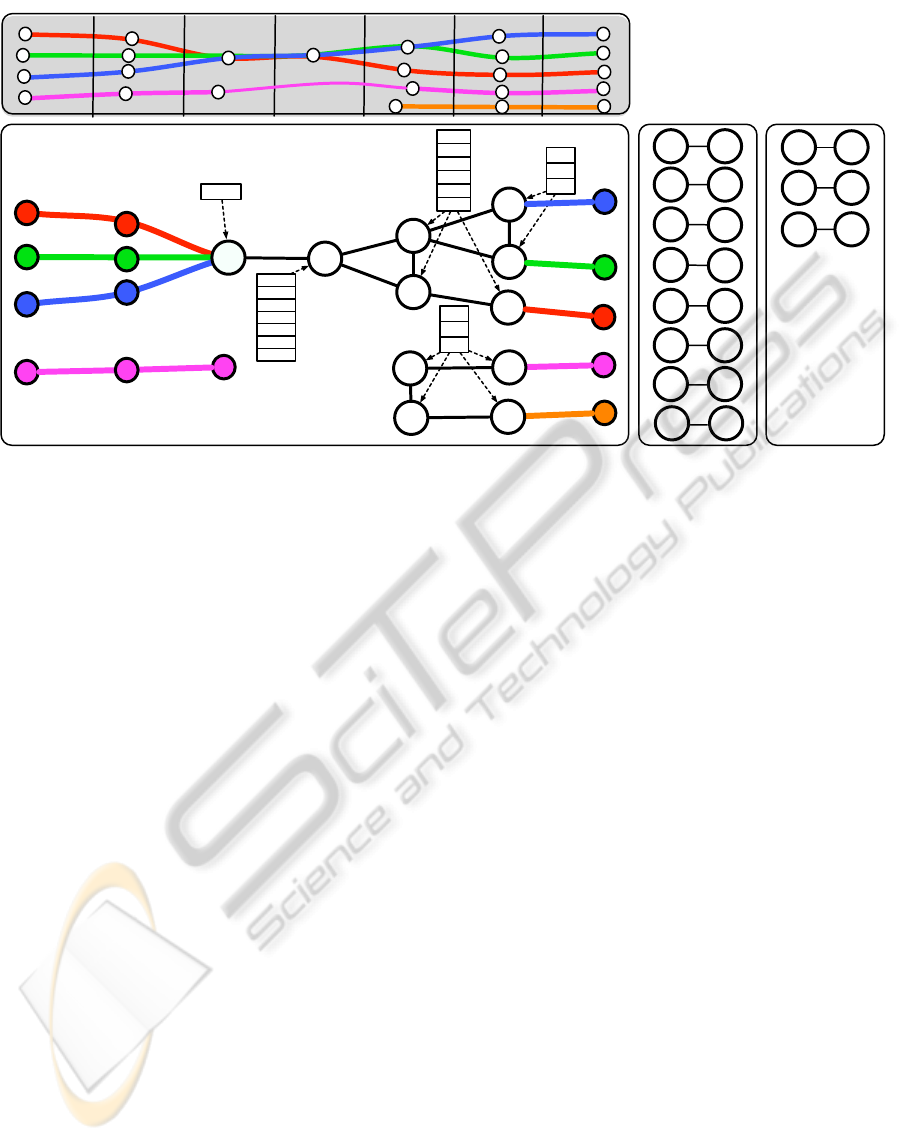
3.1 Hypothesis Graph
We define an Hypothesis Graph as an undirected
graph G = (V, E) over sets of vertices V ⊂ O that rep-
resent ambiguous observations. The set E of graph
edges contains pairs (a, b) of node indexes, and de-
notes dependency relationships between the graph
nodes. We identify two types of dependencies: La-
bel Smoothing, and Identity Coherence, respectively
grouped in sets E
ls
, E
ic
∈ E, as we will explain in Sec-
tion 3.2. Figure 6 shows an example of Hypothesis
Graph.
We say an observation o
k
a
∈ V , if any of the fol-
lowing statements is true:
• The measurement is the result of a splitting.
• The measurement comes from multiple tracks.
• The observation o
k−1
a
was also ambiguous.
• It is the first measurement of the tracklet, and exist
occluded tracklets in past frames which are candi-
dates to be recovered.
Let Z = {Z
1
, Z
2
, ..., Z
n
} be a vector of multidimen-
sional random variables, each corresponding to a ver-
tex from the Hypothesis Graph, and M be the set of all
motion vectors. Each variable realization Z indexes
one of the possible hypothesis present in its associ-
ated ambiguous observation. An Hypothesis h is de-
fined as a set of an arbitrary number of track labels
{l
1
, l
2
, ...}. The goal is to label each ambiguous vari-
able with the most probable hypothesis.
We propose a similar probabilistic approach to the
one presented in Section 2. The set of most likely
hypothesis for each of the ambiguous measurements
maximizes the posterior probability,
P(Z|M) = P(M|Z)P(Z) (14)
where the likelihood function takes the form:
MULTIPLE TARGET TRACKING AND IDENTITY LINKING UNDER SPLIT, MERGE AND OCCLUSION OF
TARGETS AND OBSERVATIONS
19
4
1
3
2
4
1
2
3
4
3
2
1
4
3
2
1
1,2,3
2,3
1,3
1,2
3
2
1
2,3
1,3
1,2
3
2
1
5
t
=1 2 3 4 5 6 7
(a) (b) (c)
6
5
4
Z
5
b
Z
5
c
Z
6
c
Z
5
d
Z
5
e
Z
6
f
Z
6
g
Z
6
d
Z
6
e
Z
3
a
Z
4
a
Z
3
a
1,2,3
h1
h2
h7
........
Z
4
a
Z
4
a
Z
5
b
Z
4
a
Z
5
c
Z
5
b
Z
6
f
Z
5
b
Z
6
g
Z
5
c
Z
6
c
Z
5
d
Z
6
d
Z
5
e
Z
6
e
Z
5
b
Z
5
c
Z
5
d
Z
5
e
Z
6
f
Z
6
g
Figure 6: Example of Hypothesis Graph, in the presence of several ambiguous events. The (a) top shows 7 frames with white
circles representing the observations and colored lines indicating the track each target follows. The dotted segment represents
an occlusion. In (a) bottom, the Hypothesis Graph is represented. A white circle denotes a vertex of the Hypothesis Graph (an
observation whose track label is unknown). The tables associated with such vertices show the list of hypothesis at each time
step. In (b) the label Smoothing Dependencies are shown, and in (c) the set of Identity Coherence dependencies. Best viewed
in color.
P(M|Z) =
∏
o
k
a
∈V
P(M
k
a
|Z
k
a
)
∏
o
k
a
,o
k+1
a
∈E
ls
P(M
k
a
|Z
k
a
, Z
k+1
a
).
(15)
The first likelihood term models the probability of
the measurement M
k
a
belonging to a track listed in
any available hypothesis of Z
k
a
. The second, imposes
a smoothing constraint on the track label values be-
tween two contiguous observations, as well as mod-
eling the probability of a track departure from an hy-
pothesis. The smoothing constraint will be introduced
in the next section. The first component is defined as:
P(M
k
a
|Z
k
a
) =
∏
h∈Z
k
a
∏
l∈h
P(M
k
a
|l) (16)
where,
p(M
k
a
|l) = βN (|M
k
a
− M
j
(l)|;µ
1
(m), σ
1
(m))+ (17)
(1 − β)N (
\
M
k
a
, M
j
(l);µ
2
(m), σ
2
(m)).
The measurement M
j
(l) denotes the motion vec-
tor of the last detected observation which could be
labeled with complet certainty as belonging to track
l. The term encourages the selection of hypothetic
tracks, whose motion vectors are similar to the orig-
inal non-ambiguous track, in terms of direction and
speed. The index j denotes the frame where the ob-
servation was detected, and m = k − j refers to the age
of the original measurement, influencing the shape of
the normal distributions. This allows certain variabil-
ity of the target movement depending on how long
ago the last certain measurement of track l was de-
tected. The weight β weights the contribution of the
speed or the direction.
3.2 Pairwise Potentials
We define two types of dependencies:
Label Smoothing. The label smoothing depen-
dency favors a consistent labeling of ambiguous ob-
servations along time, and encourages the generation
of long tracks by smoothing the label value between
contiguous observations within a tracklet (See Figure
6.(b)) Bring to mind the formulation of the likelihood
of a measurement belonging to an hypothesis in Eq.
(15). The Smoothing term is then defined as
P(M
k
a
|Z
k
a
= h
1
, Z
k+1
a
= h
2
) = (18)
=
1 if h
1
= h
2
P(o
k
a
|h
1
, h
2
)
|h
1
|−|h
2
|
if |h
1
| > |h
2
|
0 otherwise.
This equation enforces continuity on the track la-
bels between contiguous observations from different
frames. Note that given two hypothesis h
1
, h
2
from
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
20

two connected nodes, we enforce the same track la-
bels to appear in both hypothesis (smoothing). If the
newest hypothesis has fewer number of track labels,
we model the probability of a track disappearing with
the term P(o
k
a
|h
1
, h
2
), which is a normal distribution
constructed around the assumption that tracks close to
the image borders are likely to disappear. Any other
configuration is considered incoherent and forbidden.
Identity Coherence. The Identity Coherence is re-
sponsible of ensuring that two or more observations in
the same frame, whose hypothesis realizations can be
contradictory (e.g contain the same identity), will be
coherent after the inference. Since it is independent of
the observations, it acts as the prior of the probability
of Eq.(14):
P(Z) =
∏
o
k
a
,o
k
b
∈E
ic
P(Z
k
a
, Z
k
b
), (19)
where
P(Z
k
a
= h
1
, Z
k
b
= h
2
) =
1 if h
1
∩ h
2
=
/
0
0 otherwise.
These pairwise terms are represented in Figure
6.(c). Notice that in some tracking applications this
constraint does not exist (e.g. sobresegmentation pro-
duces several measurements of one target). We al-
low this restriction to be dropped depending on the
tracking application. Furthermore, the Identity Co-
herence restriction can be selectively placed to distin-
guish both cases: grouping measurements of the same
target, and mutual-occlusions of targets.
3.3 Handling of Long Occlusions
The last important detail to complete the method for-
mulation is the handling of long occlusions. We ad-
dress this issue with a very intuitive assumption: Ev-
ery observation which starts a new tracklet is a can-
didate to contain the identity of track which ceased
being observed during the last L frames. Lets denote
as T
occ
the list of these track identities, and let Z
k
a
be
the observation of a new tracklet a detected in frame
k. Being N the number of tracks identified up to the
present frame, the set of realizations (hypothesis) of
Z
k
a
is defined as
Z
k
a
= {T
occ
∪ {N + 1}}. (20)
The Eq. (16) is then slightly modified to include
the likelihood of a new track appearing in the scene:
P(M
k
a
|Z
k
a
) =
∏
h∈Z
k
a
∏
l∈h
P(M
k
a
|l) if l ∈ T
occ
P
new
(M
k
a
) if l = N + 1
(21)
Note that the distribution stays unchanged if the
realization of Z
k
a
suggests the recovery of an occluded
track in T
occ
. Otherwise, the density P
new
indicates
the probability of detecting a new track. The distribu-
tion P
new
is assumed normal, defined on the minimum
distance between the feature centroid and the near-
est image border. Analogously to the departures, the
entrance of targets is more likely in the limits of the
image.
4 LEARNING AND
IMPLEMENTATION
All probability densities assumed Gaussian are
learned from training data using Maximum Like-
lihood Estimation. The densities which can take
an arbitrary shape are as well learned using a non-
parametric method like Kernel Density Estimator.
The training data is annotated manually using a soft-
ware specifically developed for that purpose.
In order to infer the most likely configuration of
random variable values, we construct two Markov
Random Fields, each of them representing the pos-
terior probability for one of the layers: tracklet gener-
ation and data association. The maximization of both
posteriors of Eq. (2) is usually NP-Hard. To over-
come this problem, we approximate the solution us-
ing the Tree Reweighed Belief Propagation, which is
a message passing algorithm which infers the Maxi-
mum a Posteriori configuration of the set of variable
realizations. We use a C++ implementation of the al-
gorithm (libDAI), developed in (Mooij, 2010).
5 EXPERIMENTS AND RESULTS
We evaluate our Multiple Target Tracking algorithm
in experiments on synthetic and real image sequences,
and provide quantitative results of the experiments.
Usually works on Multiple Target Tracking use stan-
dard metrics to evaluate the error on the prediction
of the localization of the targets in each frame. A
popular approach in recent works suggests the use of
MOT Metrics to evaluate MTT precision and accu-
racy (Bernardin and Stiefelhagen, 2008). This mea-
sure takes into account four different aspects of the
quality of the results:
• Precision of the hypothesis localization.
• False positive errors.
• Missed detections.
• Number of track label miss-matches.
MULTIPLE TARGET TRACKING AND IDENTITY LINKING UNDER SPLIT, MERGE AND OCCLUSION OF
TARGETS AND OBSERVATIONS
21

An important difference between our experimen-
tal demonstration against other examples shown in the
literature is that we do not include a detection phase in
the tracking process. This means that we do not filter
the objects that appear in the image, and thus we con-
sider every observation as a potential target to track.
This is justified due to the nature of the applications
we are dealing with. In the synthetic scenario it is
obvious that all the objects present in the images are
valid targets, since we do not introduce any artificial
clutter or noise. In the headlight tracking application,
we threshold the intensity values of the images to dis-
cern the interesting blobs, and we track indistinctiv-
elly every light, and every reflection, which are both
present in our ground-truth as valid targets. In the last
example, the bacteria growth sequence, we manually
construct a perfect segmentation, which does not pro-
duce any undesired artifacts.
Therefore, we cannot evaluate the precision of our
hypothesis, since the hypothesis location is always the
same as the target location. A target cannot be miss-
detected, since non-occluded targets have at least one
observation, and every detection has at least one target
associated, meaning that false-positives cannot occur.
The only MOT component that we can use as a quality
measure is the number of track label miss-matches.
Moreover, we also measure the accuracy of tracklet
generation using a typical feature-matching evalua-
tion metric, by simply counting the ratio of correct
matchings against the total. Table 3 shows the quan-
titative results for the experiments.
5.1 Synthetic Sequences
We have generated two synthetic sequences of 100
frames, each containing a number of targets imaged
as a circle with a fixed radius. The sequence A con-
tains an average of 10 particles per frame, the se-
quence B, 15 particles per frame. The radius of the
particles is 10 and 5 for each sequence respectively.
Figure 7 shows a timestamp of 20 contiguous frames
of both sequences. In the first sequence the motion is
achieved with a XZ projection of a 3D helical motion
of targets. In the second the particles move towards a
sink in the center of the image . It can be seen how
the particles follow more or less linear trajectories in
both cases. Each color represents a track label. Sud-
den changes of colors, or sharp corners along tracks,
indicate a miss-match of track labels.
5.2 Tracking of Car Headlights
In the context of an Intelligent Headlight Control Ap-
plication, the main problem is to classify a blob in the
(a)
(b)
Figure 7: Timestamp of 20 frames in both synthetic tracking
sequences. In (a), targets move from left to right disappear-
ing in the right image border. In (b),targets move from the
image borders towards the image center, where they disap-
pear.
image as a car or a reflection, in order to automate the
activation of the light beams. Usually, a complex clas-
sifier gathers features from every blob in the image,
and labels them as vehicle or non-vehicle. A tracker
can also be included working in parallel with the clas-
sifier (Rubio and Serrat., 2010), in order to provide
additional information (e.g combining the classifier
beliefs of a given target between different frames).
This is the reason why, in this specific application,
we are interested of tracking every blob in the image,
and there is no need to perform a detection process.
We perform multiple target tracking in two se-
quences of 100 frames each. Note that this scenario
is specially difficult because the camera recording the
images is constantly moving, since it is mounted in
a car. Far away lights are represented as very tiny
blobs of few pixels that are very hard to track. Classic
trackers like Kalman Filter would certainly perform
poorly in this situation, since measurements of dis-
tant targets are separated by a few image pixels, and
the movement of the camera makes very hard to solve
the data association. Moreover, there are hardly any
appearance features to rely on.
5.3 Bacteria Growth
This experiment consists of tracking a growing num-
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
22
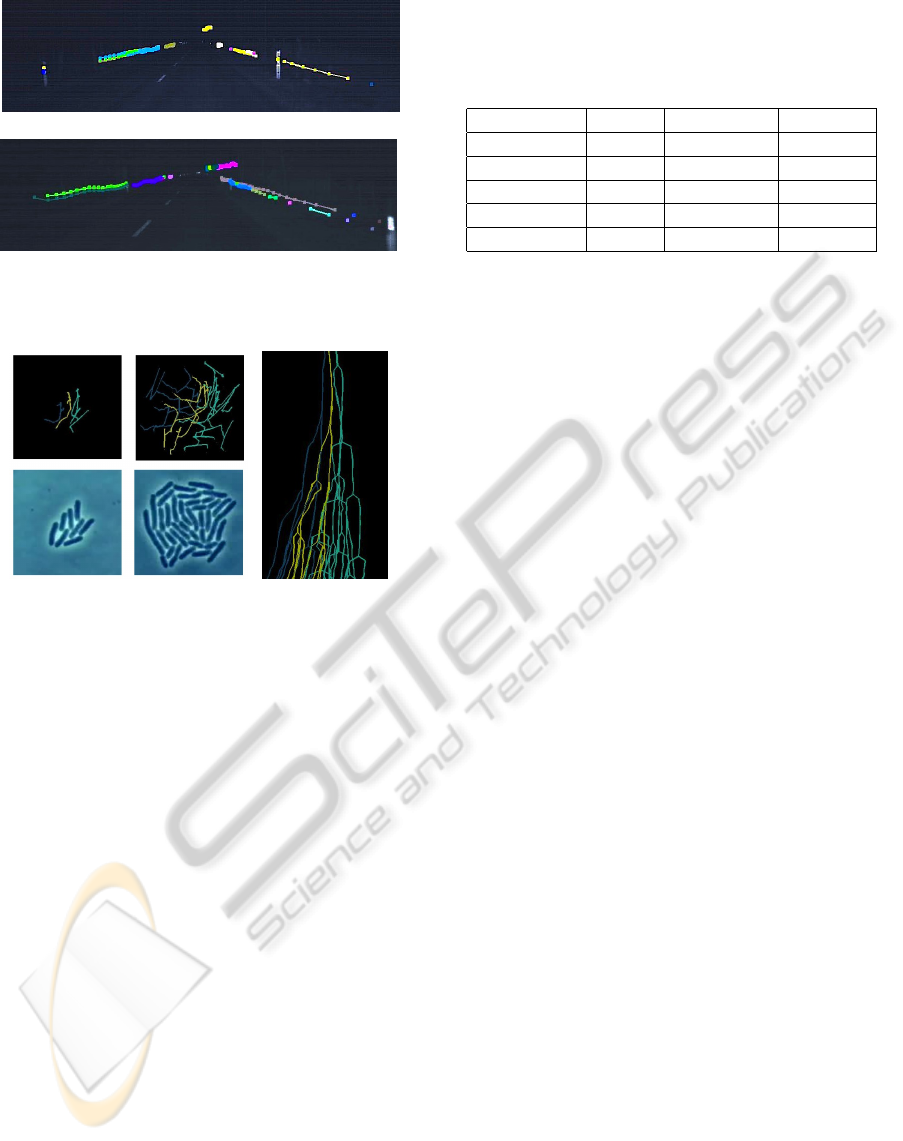
(a)
(b)
Figure 8: Representation of the target tracks in both head-
lights sequences. Each color represents a different label.
(a) (b)
Figure 9: In (a), bottom, two frames of the bacteria growth
sequence. In (a) top, the corresponding paths. The three dif-
ferent colors indicate the original bacteria parent that origi-
nated the track. In (b), it is represented the lineage tree, by
plotting each track’s horizontal component against time.
ber of bacteria, which are continuously dividing in
two. This is an example of a tracking scenario where a
target can become two, and we are interested in track-
ing these targets at the same time that we construct
what is known as the cell mitosis lineage. The se-
quence provided has 54 frames, reaching in the last
frame a maximum of 43 targets simultaneously in the
image.
In this application we slightly modify the appear-
ance likelihood of Eq. (4), to improve the results,
by profiting from the little appearance information
that the targets display. We use the overlap ratio be-
tween the pixel areas the bacteria cover in consecutive
frames, to determine the most likely correspondence
between bacteria.
6 CONCLUSIONS AND FURTHER
WORK
In this paper we have modeled the problem of Mul-
tiple Target Tracking with presence of occlusions,
Table 3: Results for every video sequence. First column
shows the total number of objects that appear in the se-
quence. Second column the ratio of incorrect tracklets.
Third column shows number of track label miss-matches
against total number of objects.
Application N. Obj % Trackets % Labels
Synthetic1 36 0.12 0.16
Synthetic2 52 0.19 0.27
Headlights1 29 0.31 0.24
Headlights2 35 0.27 0.34
Bacteria 43 0 0.11
merges and splits, as a two stage probabilistic method.
The probability densities that model the target behav-
ior and data association are all learnt form training
data. We have provided insights into the different sce-
narios one can find when dealing with the problem of
Tracking, and we also present our model as a general
solution to deal with different tracking scenarios si-
multaneously. We have proved the suitability of our
approach in three different experiments, one synthetic
and two with real images, in which we track parti-
cles presenting non or very poor appearance features.
This makes it a challenging problem, mainly when
addressing the data association of objects and obser-
vations.
Avenues for future research include increasing the
quantity and quality of experiments, covering a wider
spectrum of tracking scenarios. Moreover, introduc-
ing a detector in the model will allow our method to
be applied in a large range of classic tracking applica-
tions, as well as qualifying it to follow standard eval-
uation metrics and benchmarks of the state of the art
of the MTT.
ACKNOWLEDGEMENTS
This work was partially founded by Universitat
Aut
`
onoma de Barcelona and by Spanish MICINN
projects TRA2011-29454-C03-01, TIN2011-29494-
C03-02, and Consolider Ingenio 2010: MIPRCV
(CSD200700018).
REFERENCES
Benfold, B. and Reid, I. (2011). Stable multi-target tracking
in real-time surveillance video. In CVPR, pages 3457–
3464.
Bernardin, K. and Stiefelhagen, R. (2008). Evaluating mul-
tiple object tracking performance: the clear mot met-
rics. J. Image Video Process., 2008:1:1–1:10.
Khan, Z., Balch, T., and Dellaert, F. (2003). An mcmc-
MULTIPLE TARGET TRACKING AND IDENTITY LINKING UNDER SPLIT, MERGE AND OCCLUSION OF
TARGETS AND OBSERVATIONS
23

based particle filter for tracking multiple interacting
targets. In in Proc. ECCV, pages 279–290.
Kuhn, H. W. (1955). The Hungarian method for the assign-
ment problem. Naval Research Logistic Quarterly,
2:83–97.
Laet, T. D., Bruyninckx, H., and Schutter, J. D. (2011).
Shape-based online multitarget tracking and detec-
tion for targets causing multiple measurements: Vari-
ational bayesian clustering and lossless data associa-
tion. IEEE Transactions on Pattern Analysis and Ma-
chine Intelligence, 99.
Li, K., Chen, M., and Kanade, T. (2007). Cell population
tracking and lineage construction with spatiotemporal
context. In Proceedings of the 10th International Con-
ference on Medical Image Computing and Computer-
Assisted Intervention (MICCAI), pages 295 – 302.
Liu, M., Roy Chowdhury, A., and Reddy, G. (2009). Ro-
bust estimation of stem cell lineages using local graph
matching. In MMBIA09, pages 194–201.
Mooij, J. M. (2010). libDAI: A free and open source C++
library for discrete approximate inference in graphi-
cal models. Journal of Machine Learning Research,
pages 2169–2173.
Nillius, P., Sullivan, J., and Carlsson, S. (2006). Multi-target
tracking - linking identities using bayesian network in-
ference. In In: Proc. IEEE Conf. on Computer Vision
and Pattern Recognition, pages 2187–2194.
Reid, D. B. (1979). An algorithm for tracking multiple
targets. IEEE Transactions on Automatic Control,
24:843–854.
Rubio, J. C., A. L. D. P. and Serrat., J. (2010). Multiple
target tracking for intelligent headlights control. In
Intelligent Transportation Systems Conference, 2010.
ITSC 2010. IEEE.
T.Fortmann, Bar-Shalom, Y., and Scheffe, M. (1983). Sonar
tracking of multiple targets using joint probabilistic
data association. IEEE Journal of Oceanic Engineer-
ing, 8:173–184.
Zheng Wu, T. H. K. and Betke, M. (2011). Efficient track
linking methods for track graphs using network-flow
and set-cover thechniques. in CVPR.
ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods
24
