FLOW AND PARTICLE

DEPOSITION IN THE TURBUHALER DPI

A CFD Simulation

J. Milenkovic

, A. H. Alexopoulos

and C. Kiparissides

CPERI, CERTH, 6

km Harilaou-Thermi rd., Thermi, Greece

Department of Chemical Engineering, Aristotle University of Thessaloniki, Thessaloniki, Greece

Keywords: Dry Powder Inhaler, Turbuhaler, CFD, Deposition.

Abstract: In this work the steady-state flow in a commercial dry powder inhaler device (i.e.., Turbuhaler) is described.

The DPI geometry is constructed in a CAD/CAM environment (i.e., CATIA v5) and then imported into

GAMBIT where the geometry is discretized into a computational grid. The Navier-Stokes equations are

solved using FLUENT (v6.3) and particle motion and deposition are described using an Eulerian-

fluid/Lagrangian-particle approach. Flow and particle deposition for a range of mouthpiece pressure drops

(i.e., 800-8800Pa), as well as particle sizes corresponding to single particles and aggregates (i.e., 0.5-20μm)

are examined. The total volumetric outflow rate, the overall particle deposition as well as the particle

deposition sites in the DPI are determined. The simulation results are found to agree well with available

experimental data for volumetric flow and overall particle deposition.

1 INTRODUCTION

Dry Powder Inhalers, DPIs, are one of the principle

means of delivering pharmaceuticals due to their

ease of use and cost-effectiveness. The main

function of a DPI device is the adequate dispersion

and delivery of particles. Initially the particles are in

the form of a loose powder which, under the action

of airflow is broken up and dispersed as particle

aggregates which are then further broken up into

fine particles (Ashurst et al. 2000; Newman and

Busse, 2002; Tobyn et al., 2004; Islam et al., 2008;

Alagusundaram et al.,

2010). Powder properties, e.g.,

cohesion, charge, size, and size distribution,

influence powder dispersion and the breakage of

particle agglomerates (French et al., 1996; Zeng et

al., 2000; Finlay, 2001; Newman and Busse, 2002;

Chan, 2006)

One of the common problems with DPIs is the

loss of powder/drug due to deposition within the

device. In order to provide the maximum drug dose

per inhalation and to ensure minimal dose-to-dose

variation it is necessary to minimize the drug losses

due to internal deposition. It is also desired to have

good control over the dispersibility of the powder,

release of drug (when attached to powder particles),

and breakup of agglomerates in order to achieve the

desired particle/agglomerate size distributions at the

DPI mouthpiece outflow (Alagusundaram et al.,

2010). Consequently, if the underlying processes are

better understood one can achieve the desired

outflow particle distribution which will conceivably

minimize oropharyngeal losses and also permit

better targeting for drug delivery in the respiratory

tract.

Due to the complex and transient flow structures

observed in most commercial DPIs as well as the

dynamic powder breakup and dispersion processes

only a small number of computational fluid

dynamics, CFD, investigations have been conducted

(Schuler et al., 1999; Ligotke, 2002). Systematic

computational studies have led to a better

understanding of the function of DPI devices. For

example, Coates et al. (2004, 2005, 2006) studied

the Aerolizer DPI in detail including the effects of

air-intake, mouthpiece, and internal grid which led

to improvements in the design and function of the

DPI. Recently, the discrete element method, DEM,

coupled to continuous phase-models has been

implemented to describe the powder dispersion

process within the inhaler (Tong et al., 2010; Calvert

et al., 2011). From the current state-of-the-art it is

Milenkovic J., Alexopoulos A. and Kiparissides C..

FLOW AND PARTICLE DEPOSITION IN THE TURBUHALER DPI - A CFD Simulation.

DOI: 10.5220/0003711600050013

In Proceedings of the International Conference on Biomedical Electronics and Devices (BIODEVICES-2012), pages 5-13

ISBN: 978-989-8425-91-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

clear that the proper description of the agglomerate

strength as well as the particle/agglomerate

interaction with the inhaler walls are key processes

that determine the final dispersion and size

distribution of pharmaceutical powders (Adi et al.,

2011).

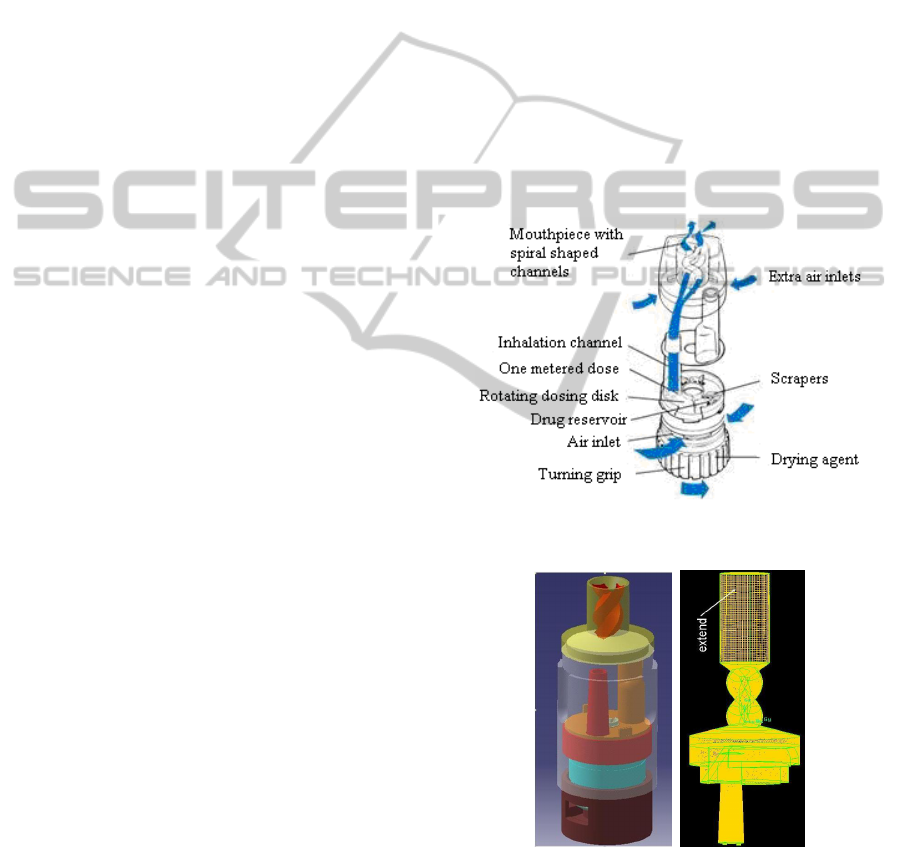
The Turbuhaler (AstraZeneca) is a multidose dry

powder inhaler that is widely used to deliver a

number of drugs (typically for asthma), e.g.,

terbutaline sulphate, (as Bricanyl), or budesonide (as

Pulmicort), to the upper respiratory tract (Wetterlin,

1988). Each dose is initially in the form of loosely

packed particle agglomerates, ~10-20μm in size,

which are released into a mixing/dispersion

chamber, where they are broken up into particles,

~1μm in size, which are then directed to the

inhalation channel of the device (Tsima et al., 1994;

Wetterlin, 1988). The proper function of the

Turbuhaler is dependent on the dynamic volumetric

flow as well as the peak inspiratory flow rate

attained during inhalation, the amount of particles

lost due to deposition within the device, and the

adequate dispersion and breakup of the powder

agglomerates in the airflow exiting the mouthpiece.

Recent experimental investigations have provided

detailed information on particle capture as well as

the percent and size distribution of escaped particles

in the outlet flow (de Koning et al., 2001; Hoe et al.,

2009; Abdelrahim, 2010).

In this work the steady airflow in a Turbuhaler

DPI is determined by CFD simulations and particle

motion as well as deposition is determined by

Eulerian-fluid/Lagrangian-particle simulations. In

what follows the DPI geometry, the discretization

procedure, and the CFD simulations are described in

detail. Next the results for steady-state airflow are

presented follow by the results for particle

deposition. Finally, the computational results are

compared to available experimental data.

2 RESULTS

The Turbuhaler DPI geometry was constructed in a

CAD/CAM environment (i.e., CATIA v5 R19) and

then imported into GAMBIT (v2.1) where a series of

computational grids were constructed consisting of

–

tetrahedral cells with a maximum

skewness of 0.85 (Figures 1 and 2). The

computational grids were originally refined in

regions where large gradients of flow were expected.

Further refinement was conducted within FLUENT

based on actual velocity gradients observed in initial

solutions.

The Navier-Stokes equations for airflow were solved

using the commercial CFD software (i.e., FLUENT

v6.3). The SIMPLEC scheme was employed to

describe pressure-velocity coupling. Second order

discretization was used for pressure and third order

MUSCL for momentum and turbulent variables.

Convergence of CFD simulations was assumed

when the residuals were < 10

-4

. Zero gauge pressure

boundary conditions were employed at all the

inflows, i.e., two powder loaded cylinders (see

bottom of Figure 2b) and four extra air inlets in the

DPI dispersion chamber (see Figure 1). Different

steady state airflows were simulated by imposing a

wide range of pressure drops at the mouthpiece

outflow ranging from 800 to 8800Pa which

corresponded to volumetric flow rates of 20 to 70

l/min. Steady-state airflow can be considered an

approximation to dynamic inhalations where the

flow rate has approached the peak inspiratory value.

Figure 1: Turbuhaler Dry Powder Inhaler.

Figure 2: Turbuhaler Dry Powder Inhaler Geometry and

Grid (1 10

tetrahedral cells).

Eulerian-fluid/Lagrangian-particle simulations of

particle motion and deposition were conducted for

particles between 0.5-20μm in size encompassing

the single particle and particle agglomerate size

BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices

ranges of typical pharmaceutical powders employed

in the Turbuhaler. Particles were assumed to be

released instantaneously at t = 0 and uniformly from

a surface located immediately upstream from the

powder storage site. Powder dispersion was assumed

to occur instantaneously after which no further

breakage occurred. Consequently, particles in

motion were taken to be constant in size. Upon

collision with the inhaler walls particles either

deposited or reflected. No collision-induced

breakage was examined in this work. The capture

efficiency of particles with the inhaler walls was

assumed to be either equal to one or a function of the

velocity magnitude.

2.1 Simulations of Airflow

in the Turbuhaler DPI

According to the range of volumetric airflows

examined in this work, e.g. Q = 20 - 70l/min, the

local Reynolds numbers, Re = Q ρ / μ A

1/2

, where ρ

and μ are the density and the viscosity of air and A is

the cross-sectional area, ranged from 130-16,000.

Consequently the transitional SST k-ω model was

employed to describe the transitional turbulent flows

encountered in the DPI.

Computational grids varying between 2 10

and

2 10

tetrahedral elements were employed to test for

convergence. The 1 10

grid was found to provide

essentially identical results as the 2 10

grid and was

used for the results presented in this paper. It should

be noted that the computational grid was extended

from the mouthpiece by 20mm in order to minimize

recirculation effects at the outflow surface and to

improve convergence behaviour.

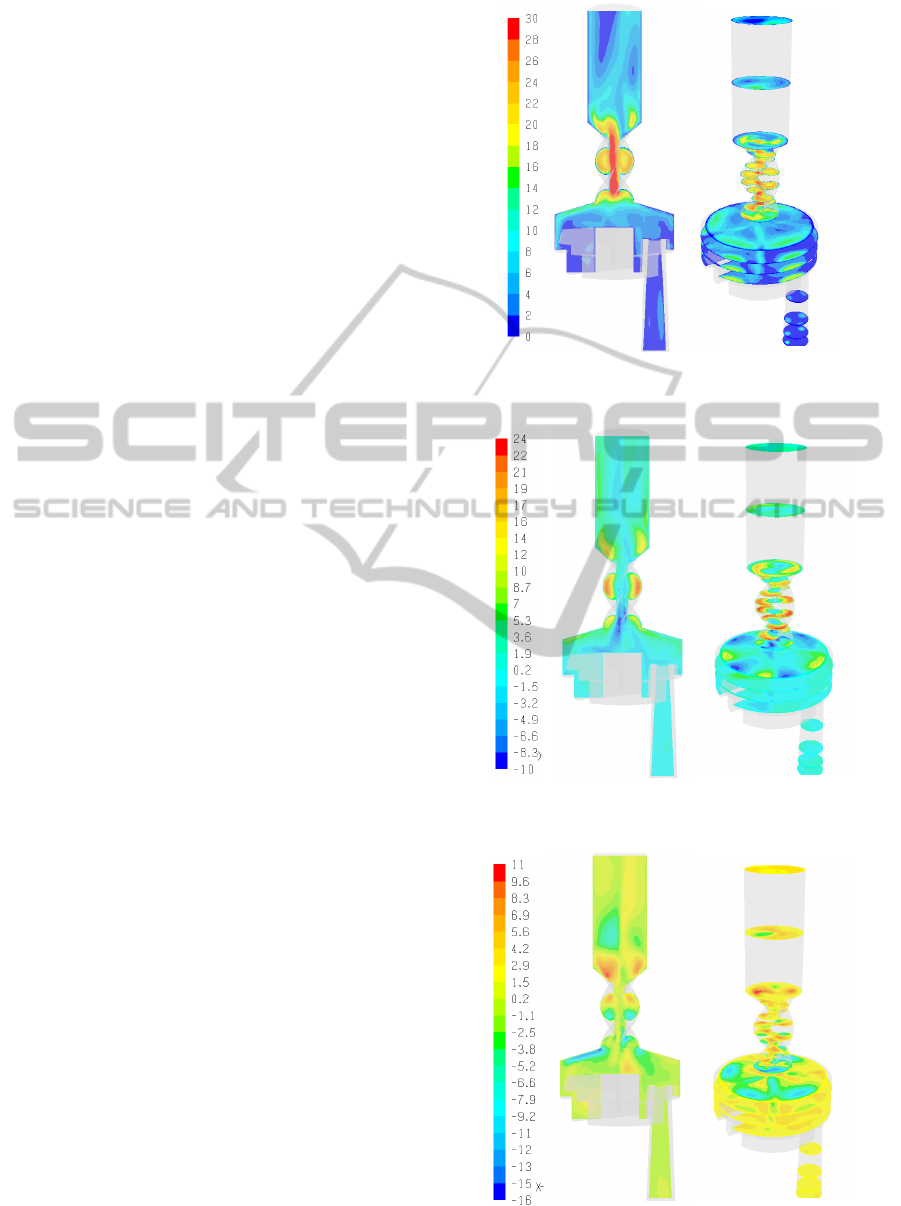
In Figures 3-5 the velocity magnitudes as well as

the tangential and radial velocities are displayed

along an axial (i.e., zx) plane and several planes

normal to the z-axis (i.e., xy sections). As can be

observed, the airflow in the DPI device is found to

be laminar in the inhalation channel with two jet

flows emanating from the powder storage cylinders.

In the dispersion chamber the flow is characterized

by large eddies and secondary flows. In the spiral

region significant tangential flows develop and

persist about halfway up the mouthpiece extension.

The tangential motion induced by the spiral airway

in the mouthpiece is significant reaching 83% of the

maximum velocity magnitude. It should be noted

that the velocity profiles observed for larger flow

rates, e.g., 60 l/min, are qualitatively similar.

Figure 3: Velocity magnitude in the Turbuhaler DPI

(mouthpiece pressure drop ΔP = 800Pa).

Figure 4: Tangential velocity in the Turbuhaler DPI

(ΔP = 800Pa).

Figure 5: Radial velocity in the Turbuhaler DPI

(ΔP = 800Pa).

FLOW AND PARTICLE DEPOSITION IN THE TURBUHALER DPI - A CFD Simulation

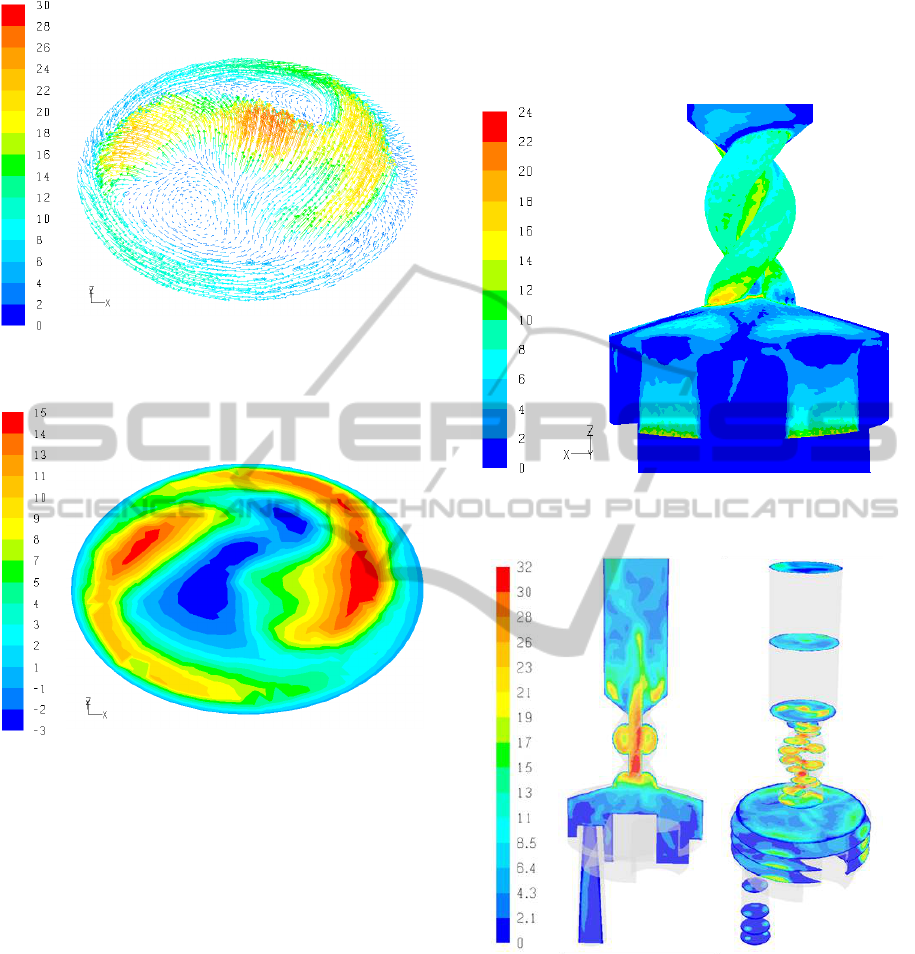
Figure 6: Velocity vectors at the mouthpiece (ΔP =

800Pa).

Figure 7: Tangential velocity at the mouthpiece

(ΔP = 800Pa).

The mouthpiece outflow of a DPI is very important

as it determines the dispersion and flow behaviour of

the particles in the oral cavity and the upper

respiratory tract and consequently influences particle

losses in the oral cavity and throat regions. In

Figures 6 and 7 the mouthpiece outflow for a

pressure drop of ΔP = 800Pa is shown in terms of

velocity magnitude and tangential velocity. It is

clear that the flow is strongly influenced from the

preceding spiral region and that the axial and

tangential components of the velocity are

nonuniform. Moreover, the strongly localized

tangential and axial airflows at the mouthpiece cause

recirculation flows in both the tangential and axial

directions, further complicating the flow.

Wall-stresses can also be determined based on the

CFD solution. In Figure 8 the wall stresses for ΔP =

800Pa are shown. It is clear that most of the wall

stresses correspond to the high flowing regions

adjacent to the dispersion chamber air inlets and

attain their maximum value at the entry and exit

regions of the spiral region.

Figure 8: Turbuhaler wall stresses.

Figure 9: Velocity magnitude in the Turbuhaler DPI –

LES results (ΔP = 800Pa).

Large Eddy Simulations, LES, fully resolve the

large scale motion of turbulent flows thus providing

more information and accurate results compared to

Reynolds Averaged Navier-Stokes approaches,

RANS, e.g., k-ε, k-ω. The computational burden of

LES is significant (e.g., at least an order of

magnitude more than with RANS models).

Consequently, only a single case (i.e., ΔP = 800Pa)

of steady-state flow of the Turbuhaler DPI was

simulated with LES using FLUENT.

BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices

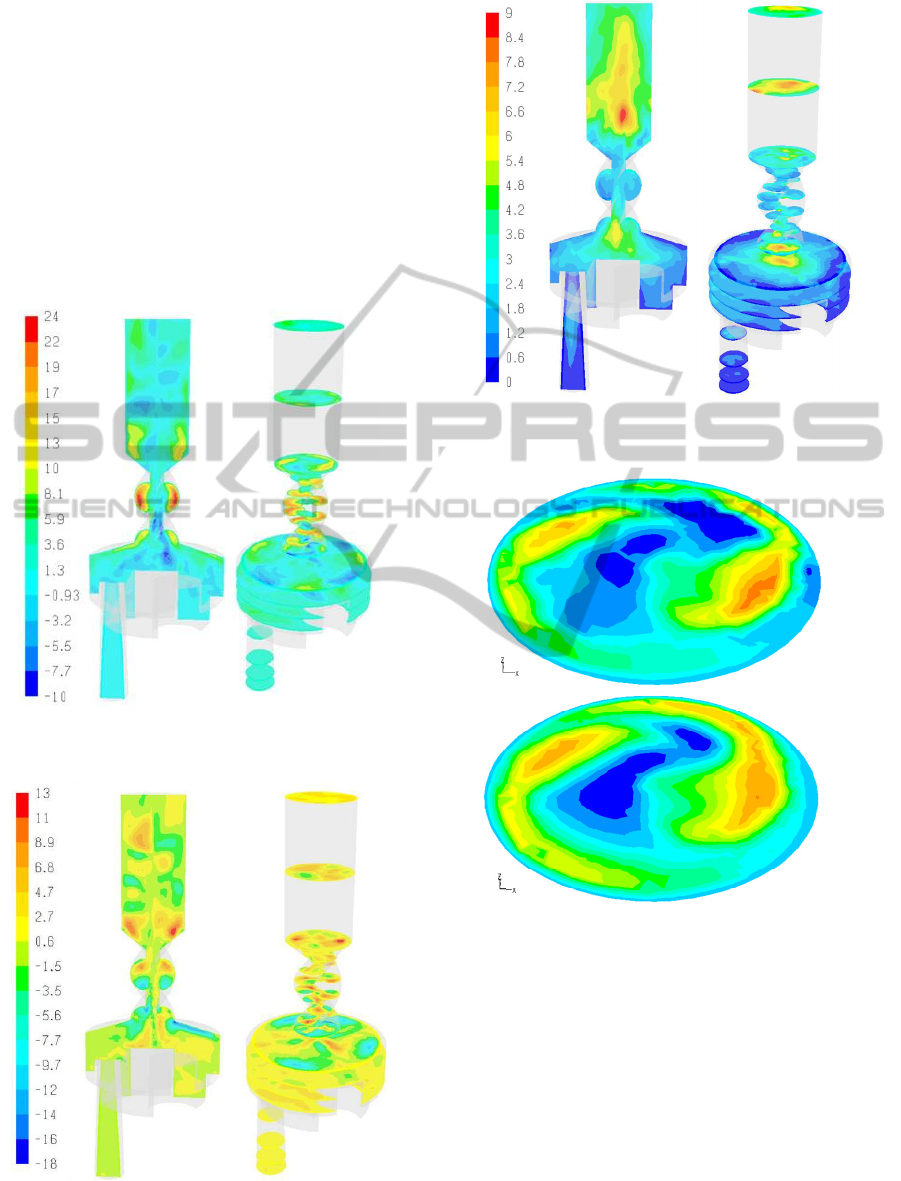
In Figure 9 the results for the mean velocity

magnitude obtained with LES is shown. The main

flow structures are similar with the k-ω SST results

in Figure 3 but, as expected, differences can be

observed in the flow details as well as in secondary

flows.

The enhanced resolution of eddies and secondary

flows with the LES is demonstrated in Figures 10

and 11 depicting the tangential and radial flow,

respectively. Compared to the radial and tangential

flows predicted with the k-ω SST model (Figures 4

and 5) there are many differences, e.g., in the large

eddies of the mouthpiece extension.

Figure 10: Tangential velocity component in the

Turbuhaler DPI – LES results (ΔP = 800Pa).

Figure 11: Radial velocity component in the Turbuhaler

DPI – LES results (ΔP = 800Pa).

Figure 12: RMS velocity magnitude in the Turbuhaler DPI

(ΔP = 800Pa).



(a)

(b)

Figure 13: Tangential velocity component at the

mouthpiece exit (ΔP = 1400Pa). (a) LES (b) k-ω SST.

In Figure 12 the magnitude of the RMS velocity

fluctuations is shown. Significant velocity

fluctuations are observed at the top of the dispersion

chamber (~6m/s) and in the mouthpiece extension

(~9m/s). The intensity of fluctuations (e.g., RMS

velocity / velocity magnitude) varies within the

device up to a value of ~50% indicating significant

local fluctuations around the mean for the length

scales of flow resolved within the LES.

The RMS fluctuations of the individual velocity

components range from 1-8m/s for the axial velocity

component and 1-4m/s for the other components

FLOW AND PARTICLE DEPOSITION IN THE TURBUHALER DPI - A CFD Simulation

with different spatial variations within the device.

These results demonstrate that the fundamental

assumption of local turbulence isotropy of the

RANS models is incorrect.

In Figure 13 the tangential velocities at the outlet

surface for ΔP=1400Pa are shown. It is clear that the

tangential velocities predicted by the k-ω SST and

LES turbulence models are very similar. In fact the

k-ω SST turbulence model provided the most similar

to the LES results compared to the other RANS

turbulence models (e.g., standard k-ε, RNG k-ε).

Consequently, despite the observed differences in

secondary flows (Figures 9-11) the k-ω SST model

was employed for all the simulations of this work. .

2.2 Simulation of Particle Motion and

Deposition in the Turbuhaler DPI

Eulerian-fluid/Lagrangian-particle simulations were

performed for all the flows examined in section 2.1.

These simulations are generally valid for particle

volume fractions <10%. For effective powder

dispersion the solids volume ratio in the DPI device

is approximately 10

-2

-10

-4

depending on the location

and the flow rate. Consequently, the particle phase

was assumed to not influence the airflow.

The total particle deposition in the DPI device

was determined assuming either a 100% capture

efficiency or a capture efficiency based on a critical

velocity magnitude. The later case was implemented

within FLUENT using a user-defined function for

the capture efficiency.

Single-sized simulations were performed with

particle sizes ranging from 0.5-20μm. Particle sizes

0.5-1.5μm correspond to individual particle

constituents of the agglomerates. Agglomerate

breakage and redispersion effects were not

considered. Instead, the agglomerates in the powder

storage cylinders were assumed to break-up rapidly

into their constituent particles. Clearly, agglomerate

breakage and flow occur simultaneously and this is

an area which requires further investigation.

The total particle deposition in the DPI was found to

be strongly dependent on particle size. For micron

sized particles inertial forces dominate the

deposition process and for particles <100μm gravity

can be ignored during the time-scale of a single

inhalation. In Figure 14 the total depositions for

single-sized particles ranging from 0.5-10μm, for a

100% capture efficiency, and for two pressure drops,

e.g., 800 and 1400Pa, are shown. Simulations

indicate that for a pressure drop of 800Pa the

deposition of 0.5-1μm particles is 19-24% but that of

agglomerates 5-10μm is 90-100%. The predicted

total particle deposition in the DPI increases with

volumetric flow to large, and unrealistic, values

(Figure 14). Smaller deposition values can be

obtained by considering less than 100% particle

capture efficiency. Other mechanisms such as

agglomerate breakage dynamics and/or redispersion

of deposited agglomerates could also result in

smaller values of particle deposition.

Figure 14: Overall particle deposition in the Turbuhaler.

Figure 15: Particle Deposition – Effect of Pressure drop.

(a) ΔP = 800Pa, (b) ΔP = 5400Pa. D = 1μm.

BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices

The spatial distribution of particles deposited on

the DPI walls was visualized using Tecplot. In

Figure 15 particle depositions for two pressure

drops, i.e., 800 and 5400Pa, are shown. Thus, the

larger pressure drop results increased velocities and

total particle deposition but also significantly

different particle deposition patterns. The increased

deposition for large pressure drops in the spiral

region is caused by the increased tangential flow in

this region.

Figure 16: Particle Deposition – Effect of Particle Size. (a)

D = 2 μm, (b) D = 5 μm. ΔP = 800Pa.

In Figure 16 the effect of particle size on the

distribution of deposited particles in the DPI device

is shown. Comparing particle sizes of 1 (see Figure

15a), 2 and 5μm (Figure 16) significant differences

in the total deposition as well as the deposition

distribution are observed. The significant particle

deposition that occurs in the mouthpiece region

(which includes the spiral region0 is actually a

common problem in many commercial DPI devices

where about half the internal deposition occurs (de

Koning et al., 2001).

The results of Figures 15 and 16 can be used to

optimize the design of the DPI. For example, the

spiral region of the Turbuhaler could be redesigned

so that smaller radial and tangential velocities

develop leading to decreased particle collisions in

this region.

0.0

0.1

0.2

0.3

0.4

Absolute Deposition

2μm

5μm

1μm

(b)

0 102030405060

Axial Position, mm

0.0

0.2

0.4

0.6

0.8

Fractional Deposition

2μm

5μm

1μm

(a)

Figure 17: Particle Deposition. (a) Fractional Cumulative

Deposition, (b) Local.Deposition (ΔP = 800Pa).

In Figure 17 the axial fractional cumulative

deposition distribution and the local fractional

deposition for ΔP = 800Pa are shown. The results

indicate significant differences in the deposition

patterns with particle size with most deposition

occurring in the dispersion chamber and the spiral

region.

2.3 Comparison to Experimental Data

The computational results of this work were

compared to the experimental results of de Koning

et al (2001) and Abdelrahim (2010) for the

Turbuhaler in terms of flow and particle deposition.

In Figure 18 the predicted steady-state volumetric

flows are plotted against the outlet pressure drop

applied at the mouthpiece. Both laminar and k-ω

SST models for flow are examined. It is clear that

both models agree very well with the experimental

data for all flow rates with the k-ω SST model being

slightly more accurate.

In Figure 19 the total, dispersion chamber, and

mouthpiece particle depositions for 1400Pa (or 30

l/min) are compared to the experimental data of de

Koning et al. (2001). A 100% capture efficiency

leads to very large total deposition values, i.e., 75%,

for this flow rate (see Figure 14) and even larger for

larger flow rates, e.g., Q>30 l/min. Consequently, in

this work the capture efficiency is related to a

FLOW AND PARTICLE DEPOSITION IN THE TURBUHALER DPI - A CFD Simulation

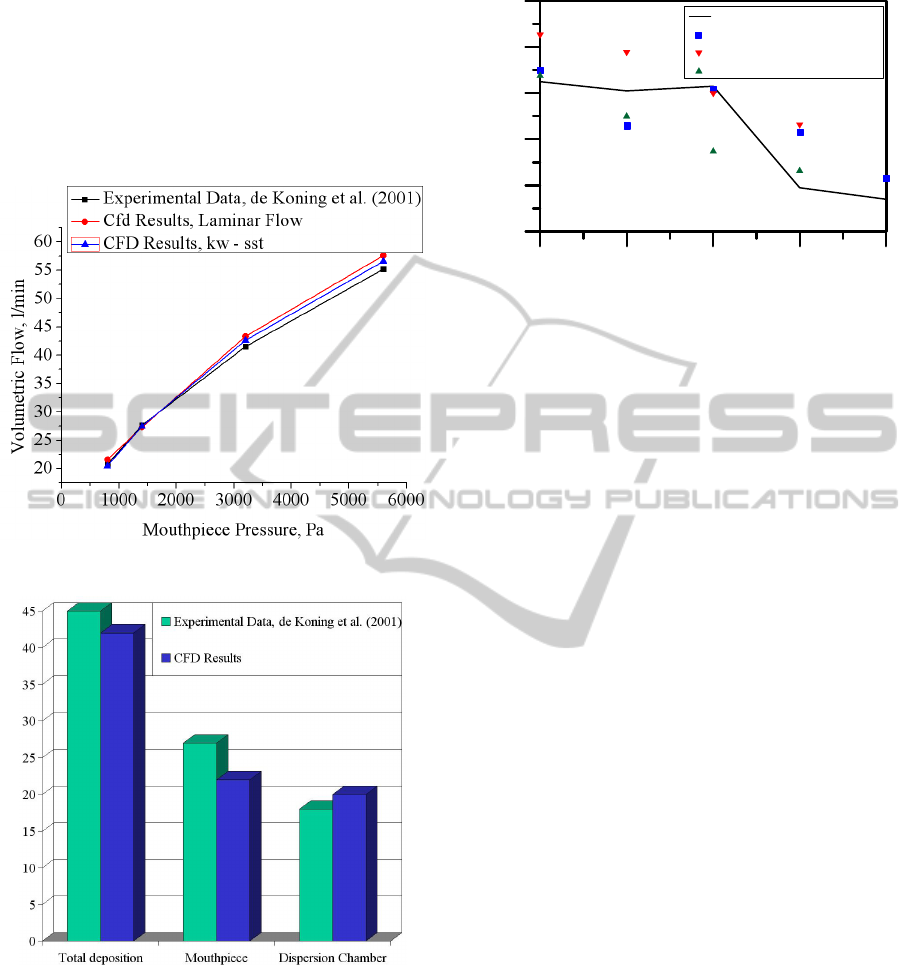
critical velocity, V

, above which particles reflect

(without deposition or momentum dissipation).

Assuming a critical velocity magnitude for

deposition, V

= 22m/s, which results in an overall

capture efficiency of ~42.5%, the mouthpiece,

dispersion chamber, and total particle deposition

results for Q = 30 l/min are in good agreement to the

experimental data.

Figure 18: Volumetric flow in the Turbuhaler.

Figure 19: Regional particle deposition in the Turbuhaler.

Q = 30 l/min. V

= 5m/s.

In Figure 20 the predicted total particle

deposition are compared to the experimental data of

de Koning et al (2001) and Abdelrahim (2010) for

flowrates Q = 30, 40, 50, 60 and 70 l/min and for

two different inspired volumes, i.e., 2 and 4l

(Abdelrahim, 2010). For a critical velocity of V

22 m/s and a particle diameter of D = 2μm the

agreement with the experimental data is good

considering the different experimental conditions

30 40 50 60 70

Flow Rate, l/min

% Total Deposition

: CFD Results

: de Koning et al. (2001)

: Abdelrahim (2010) 2l

: Abdelrahim (2010) 4l

Figure 20: Total particle deposition in the Turbuhaler. D =

2 μm. V

= 22 m/s. Comparison between experimental

results of de Koning et al. (2001), Abdelrahim (2010) and

computational CFD results.

(e.g., dynamic inhalation vs. steady state

simulations) and the simplicity of the particle

deposition model (e.g., velocity cut-off capture

efficiency and single-size size distribution).

3 CONCLUSIONS

This work has demonstrated the use of CFD to

determine the complicated airflow as well as particle

motion and deposition in the Turbuhaler DPI. As the

flow was either locally laminar or transitionally

turbulent the transitional SST k-ω model for

turbulence was employed. LES results revealed

some differences in the large eddies and secondary

flows but were otherwise closest to the k-ω SST

results. The simulations revealed complicated flows

with intense recirculation patterns in the dispersion

chamber and strong tangential flows in the spiral

region of the mouthpiece.

Particle deposition was found to depend on size

and flow rate and occurred predominantly in the

dispersion chamber and the mouthpiece. The

computational solutions were compared to

experimental data for volumetric flow and regional

deposition of de Koning et al. (2001) and good

agreement was observed for volumetric flow.

Particle deposition data were in agreement to

experimental data only for capture efficiencies less

than 100%. A simple capture efficiency model

assuming a critical velocity limit for particle capture

was found to produce total particle depositions

similar to the experimental values of de Koning et al

(2001) and Abdelrahim (2010).

Future work will involve dynamic inhalations

and will elaborate on the particle capture efficiency

BIODEVICES 2012 - International Conference on Biomedical Electronics and Devices

model. The capture efficiency can be determined

more accurately based on collision angle, velocity

magnitude, particle properties (e.g., size, shape, and

charge), surface properties (e.g., roughness, charge),

as well as particle/surface cohesion forces.

REFERENCES

Abdelrahim, ME (2010) Emitted dose and lung deposition

of inhaled terbutaline from Turbuhaler at different

conditions, Respiratory Medicine, 104, 682-689.

Alagusundaram M, N Deepthi, S Ramkanth, S

Angalaparameswari, TSM Saleem, K Gnanaprakash,

VS Thiruvengadarajan, C Madhusudhana, CM

Alagusundaram et al. (2010) Dry Powder Inhalers -

An Overview, Int. J. Res. Pharm. Sci., 1(1), 34-42.

Ashurst I, A Malton, D Prime and B Sumby (2000) Latest

advances in the development of dry powder inhalers,

PSTT, 3(7), 246-256.

Calvert G, A Hassanpour, M Ghadiri (2011) Mechanistic

analysis and computer simulation of the aerodynamic

dispersion of loose aggregates, Chemical Engineering

Research and Design, 89, 519–525.

Chan H-K (2006) Dry powder aerosol drug delivery –

Opportunities for colloid and surface scientists,

Colloids and Surfaces A: Physicochem. Eng. Aspects,

284-285, 50-55.

Coates MS, DF Fletcher, H-K Chan and JA Raper (2004)

Effect of Design on the Performance of a Dry Powder

Inhaler Using Computational Fluid Dynamics. Part 1:

Grid Structure and Mouthpiece Length, J. of

Pharmaceutical Sciences, 93, 2863–2876.

Coates MS, H-K Chan, DF Fletcher and JA Raper (2005)

Influence of Air Flow on the Performance of a Dry

Powder Inhaler Using Computational and

Experimental Analyses, Pharmaceutical Research,

22(9), 923-932.

Coates MS, H-K Chan, DF Fletcher and JA Raper (2006)

Effect of Design on the Performance of a Dry Powder

Inhaler Using Computational Fluid Dynamics. Part 2:

Air Inlet Size, J. of Pharmaceutical Sciences, 95(6),

1382-1392.

de Koning JP, MR Visser, GA Oelen, AH de Boer, ThW

van der Mark, PMJ Coenegracht, ThFJ Tromp and

HW Frijlink (2001) Effect of Peak Inspiratory Flow

and Flow Increase Rate on In Vitro Drug Deposition

from Four Dry Powder Inhaler Devices, in Dry

Powder Inhalation: Technical and Physiological

Aspects, Prescribing and Use, Thesis,

Rijksuniversiteit Groningen, Ch. 6., 83-94.

Finlay W. (2001) The Mechanics of Inhaled

Pharmaceutical Aerosols. An Introduction, Academic

Press, London.

French DL, DA Edwards and RW Niven (1996) The

Influence of Formulation on Emission Deaggregation

and Deposition of Dry Powders for Inhalation, J.

Aerosol Sci., 27(5), 769-783.

Hoe S, D Traini, H-K Chan, PM Young (2009) Measuring

charge and mass distributions in dry powder inhalers

using the electrical Next Generation Impactor (eNGI),

European J. of Pharmaceutical Science, 38, 88-94.

Islam N and E Gladki (2008) Dry powder inhalers (DPIs) -

A review of device reliability and innovation, Int. J. of

Pharmaceutics, 360, 1-11.

Ligotke MW (2002) Development and characterization of

a dry powder inhaler. In: Dalby RN, Byron PR, Peart

J, Farr SJ, editors. Respiratory drug delivery VIII, vol.

I. Tucson, AZ: Serentec Press Inc., 419–422.

Newman SP and WW Busse (2002) Evolution of dry

powder inhaler design, formulation, and performance,

Respir Med., 96(5), 293-304.

Olsson et al. Patent Application Publication. Pub. No. US

2007/0107721 A1. Pub. Date: May, 17, 2007.

Schuler C, A Bakshi, D Tuttle, A Smith, S Paboojian, H

Snyder, D Rasmussen, A Clark (1999) Inhale’s dry-

powder pulmonary drug delivery system: Challenges

to current modeling of gas-solid flows. In:

Proceedings of FEDSM99: 3rd ASME/JSME joint

fluids engineering conference and 1999 ASME Fluids

Engineering summer meeting, FEDSM99-7895.

Tobyn M, JN Staniforth, D Morton, Q Harmer and ME

Newton (2004) Active and intelligent inhaler device

development, Int. J. of Pharmaceutics 277, 31–37.

Tong ZB, RY Yang, KW Chu, AB Yu, S Adi, H-K Chan

(2010) Numerical study of the effects of particle size

and polydispersity on the agglomerate dispersion in a

cyclonic flow, Chemical Engineering Journal 164,

432–441.

Tsima MP, GP Martin, C Marriott, D Gardenton and M

Yianneskis (1994) Drug delivery to the respiratory

tract using dry powder inhaler, Int. J. of

Pharmaceutics, 101, 1-13.

Wetterlin K (1988) Turbuhaler: A New Powder Inhaler for

Administration of Drugs to the Airways.

Pharmaceutical Research, 5(8), 506-508.

Zeng X-M, GP Martin, C Marriott and J Pritchard (2000)

The influence of carrier morphology on drug delivery

by dry powder inhalers, Int. J. of Pharmaceutics, 200,

93–106.

FLOW AND PARTICLE DEPOSITION IN THE TURBUHALER DPI - A CFD Simulation