HANDLING IMPRECISE LABELS IN FEATURE SELECTION

WITH GRAPH LAPLACIAN

Gauthier Doquire and Michel Verleysen

Machine Learning Group - ICTEAM, Universit

e catholique de Louvain

Place du Levant 3, 1348 Louvain-la-Neuve, Belgium

Keywords:

Feature selection, Imprecise labels, Graph laplacian.

Abstract:

Feature selection is a preprocessing step of great importance for a lot of pattern recognition and machine learn-

ing applications, including classiﬁcation. Even if feature selection has been extensively studied for classical

problems, very little work has been done to take into account a possible imprecision or uncertainty in the

assignment of the class labels. However, such a situation can be encountered frequently in practice, especially

when the labels are given by a human expert having some doubts on the exact class value. In this paper, the

problem where each possible class for a given sample is associated with a probability is considered. A fea-

ture selection criterion based on the theory of graph Laplacian is proposed and its interest is experimentally

demonstrated when compared with basic approaches to handle such imprecise labels.

1 INTRODUCTION

The feature selection step is known to be of funda-

mental importance for classiﬁcation problems. Its ob-

jective is to get rid of irrelevant and/or redundant fea-

tures and to identify those being really useful for the

problem. The beneﬁts of feature selection for classiﬁ-

cation can be numerous and include: better prediction

performances of the classiﬁcation models, easier in-

terpretation of these models, deeper understanding of

the problems and/or reduced feature acquisition and

storage cost (Guyon and Elisseeff, 2003).

Due to its importance, feature selection has been

extensively studied in the literature, especially for

standard classiﬁcation problems, i.e. for problems

where each sample point is associated without am-

biguity to exactly one class label (see e.g. (Dash and

Liu, 1997; Kwak and Choi, 2002)). It has revealed

extremely useful in many ﬁelds among which one can

cite for example text classiﬁcation (Yang and Ped-

ersen, 1997) or gene expression based classiﬁcation

(Ding and Peng, 2003).

Quite surprisingly, to the best of our knowledge,

very few attempts have been made up to now to

achieve feature selection in problems where the class

labels are uncertainly or imprecisely speciﬁed and can

even be erroneous. However, such a situation can be

frequently encountered in practice and thus deserves

to be investigated. Indeed, it is frequent that a hu-

man supervision is required to assign labels to sample

points. This is for example the case in the medical

domain where a diagnostic has to be made based on

a micro-array or a radiography. Such a task can be

hard to perform and experts sometimes hesitate be-

tween different classes or propose a single class label

but associate it with a measure of the conﬁdence they

have in this label.

In this work, we address the problem of feature

selection in the case where an expert gives, for each

sample x

(i = 1 . . . n), a probability value p

i j

to each

possible class c

( j = 1 . . . l) such that

∑

j=1

i j

= 1 ∀i.

Such a supervision has been called possibilistic labels

in the literature; it can also be obtained by combin-

ing the opinion of several experts about the member-

ship of a point to a given class. As a concrete prob-

lem, (Denoeux and Zouhal, 2001) evokes the recog-

nition of certain transient phenomena in EEG data,

whose shapes can be very hard to distinguish from

EEG background activity, even for trained physicians;

experts can rarely be sure about the presence of such

phenomena, but can be able, however, to express a

possibility about this presence. Such labels are also

encountered in fuzzy classiﬁcation problems. Indeed

when classes are not well deﬁned, they can sometimes

be better represented by fuzzy labels, measuring the

degree of membership of the samples to each of the

classes. This is for example the case when the labels

are obtained through the fuzzy c-means clustering al-

162

Doquire G. and Verleysen M. (2012).

HANDLING IMPRECISE LABELS IN FEATURE SELECTION WITH GRAPH LAPLACIAN.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 162-169

DOI: 10.5220/0003712101620169

 SciTePress

gorithm (Bezdez and Pal, 1992).

The proposed feature selection algorithm is a

ranking technique based on the Laplacian Score (He

et al., 2006), originally introduced for feature selec-

tion in unsupervised problems. The basic idea is to

select features according to their locality preserving

power, i.e. according to how well they respect a prox-

imity measure deﬁned between samples in an arbi-

trary way. In this paper, it is shown how this criterion

can be extended to the uncertain label framework.

The rest of the paper is organized as follows.

In Section 2, related work on feature selection and

uncertain label analysis is presented. The original

Laplacian Score is described in Section 3 and the pro-

posed new criterion, called weighted Laplacian Score

(WLS), is introduced in Section 4. Section 5 presents

experimental results assessing the interest of WLS be-

fore Section 6 concludes the work.

2 RELATED WORK

As explained above, feature selection has been widely

investigated in the literature; traditional approaches

include wrapper or ﬁlter strategies. Wrappers make

use of the prediction (classiﬁcation or regression)

model to select features in order to maximize the per-

formances of this model. Such methods thus require

building a huge number of prediction models (with

potential hyperparameters to tune) and are typically

slow. However, the performances of the prediction

models with the selected features are expected to be

high (Kohavi and John, 1997).

On the other hand, ﬁlters are independent of any

prediction model; they are rather based on a relevance

criterion. The most popular of those criteria include

the correlation coefﬁcient (Hall, 1999), the mutual in-

formation (Peng et al., 2005) and other information-

theoretic quantities (Meyer et al., 2008) among many

more. Filters are in practice faster and much more

general than wrappers since they can be used prior

to any prediction model; they are considered in this

work. More recently, embedded methods, performing

simultaneously feature selection and prediction have

also raised a huge interest (Yuan and Lin, 2006) since

the publication of the original LASSO paper (Tibshi-

rani, 1996).

Classiﬁers for problems with uncertain label have

also been proposed in the literature; more speciﬁcally

the Dempster-Shafer theory of belief functions has

proven to be very successfull in this context (Denoeux

and Zouhal, 2001; Jenhani et al., 2008; C

ome et al.,

2009). Indeed, it offers a convenient and very gen-

eral way to model one’s belief about the class label

of a sample. This belief can be expressed as in this

paper but can also take more general forms as a set

of possible class labels or the probability of a class

with no additional information. Moreover, the Trans-

ferable Belief Model (Smets et al., 1991) permits to

combine elegantly the different pieces of belief con-

cerning a sample class membership.

Despite its importance, the problem of feature se-

lection with imprecise class labels has received few

attention in the literature. In (Semani et al., 2004),

the authors consider a fully supervised classiﬁcation

problem before relabelling automatically all the data

points in order to take into account the classiﬁca-

tion ambiguity. In (Wang et al., 2009), the Hilbert-

Schmidt independence criterion is used to achieve

feature selection with uncertain labels. However, the

possibility of label noise is not studied in this paper

which is rather focused on multi-label like problems.

It is worth noting that more speciﬁc weakly super-

vised problems have already been considered in the

literature. This is the case for semi-supervised prob-

lems in which a small fraction of the samples are as-

sociated with an exact class label while no label at all

is associated with the other samples (Chapelle et al.,

2006). An extension of the Laplacian Score has been

proposed for feature selection in this context (Zhao

et al., 2008) while many other methods also exist in

the literature, e.g. (Zhao and Liu, 2007).

A closely related but different problem is the one

where only pairwise constraints between samples are

given. This means that the exact class labels are un-

available but that, for some couples of points, it is

known whether or not they belong to the same class.

Here again, feature selection for this paradigm has

been achieved successfully with an extension of the

Laplacian Score (Zhang et al., 2008).

3 THE LAPLACIAN SCORE

This section brieﬂy presents the Laplacian Score, in-

troduced in (He et al., 2006) for unsupervised fea-

ture selection. As already discussed, the method aims

at selecting the features preserving at most the local

structure of the data, or, in other words, the neigh-

borood relationships between samples.

Let X be a given data set containing m samples x

(i = 1 . . . m) and f features f

(r = 1 . . . f ). Denote by

the r

feature of the i

sample of X. It is possi-

ble to build a proximity graph representing the local

structure of X. This graph consists in m nodes, each

representing a sample of X. An edge is present be-

tween node i and node j if the corresponding points

and x

in X are close, i.e. if x

is among the k nearest

HANDLING IMPRECISE LABELS IN FEATURE SELECTION WITH GRAPH LAPLACIAN

163

neighbors of x

or conversely, where k is a parameter

of the method. Traditionally, the proximity measure

used to determine the nearest neighbors of a point is

the Euclidean distance, denoted as d(., .).

Based on this proximity graph, a matrix S can be

built in the following way:

i, j

(

−

d(x

)

if x

and x

are close

0 otherwise

(1)

with t being a suitable positive constant. We also de-

ﬁne D = diag(S1), with 1 = [1 . . . 1]

, as well as the

graph Laplacian L = D − S (Chung, 1997).

The mean of each feature f

(weighted by the local

density of the data points) is then removed; the new

features are deﬁned by

= f

−

The objective of this normalisation is to prevent a

non-zero constant vector such as 1 to be assigned a

zero Laplacian score (and thus to be considered as

highly relevant) as such a feature obviously does not

contain any information. It is then possible to com-

pute the Laplacian score of each feature f

(2)

and features are ranked according to this score, in in-

creasing order.

More details can be found in the original paper

(He et al., 2006), where the authors also derive a con-

nection between (2) and the canonical Fisher score.

4 THE WEIGHTED LAPLACIAN

SCORE FOR POSSIBILISTIC

LABELS

In this section, the proposed feature selection crite-

rion for possibilistic labels is introduced. As already

stated, all the developments presented here could as

well be applied to the case where an expert only pro-

vides one class label for each point of the training set,

but associates this label with a coefﬁcient indicating

the certainty he has on his prediction. The section

ends with a theoretical justiﬁcation of the WLS.

4.1 The Proposed Algorithm

Consider again the data set X ∈ ℜ

m× f

. Each sam-

ple point x

has a single true class label c

belonging

to the set of the l possible class labels c

. . . c

. In

practice, however, this label is not precisely known.

Instead, each point x

is rather associated with a prob-

ability value p

i j

for each possible class label such that

∑

j=1

i j

= 1 ∀i. These values can be directly obtained

from an expert or come from the combination of sev-

eral experts opinions. Obviously, the probability that

two points in X have the same class label can be com-

puted as follows:

sim

i j

∑

k=1

i,k

j,k

. (3)

Thus, S

sim

i, j

is simply the scalar product between the

vectors of the labels probability for x

and x

The algorithm starts by building a graph G

sim

with

m nodes, each corresponding to a point in X. An edge

exists between node i and node j if the probability that

the two samples x

and x

have the same class label is

greater than 0.

From the matrix S

sim

, it is possible to deﬁne

sim

= diag(S

sim

1) and the graph Laplacian of G

sim

= D

sim

− S

sim

Let us then construct a matrix S

dis

∈ ℜ

m×m

, corre-

sponding to the probabilities that two samples belong

to different classes:

dis

i j

= 1 −

∑

k=1

i,k

j,k

= 1 − S

sim

i j

(4)

and let us deﬁne D

dis

= diag(S

dis

1) as well as L

dis

− S

dis

The importance of each feature f

is eventually

computed by the weighted Laplacian score that we

deﬁne to be

W LS

sim

dis

; (5)

the features can be ranked according to this score, in

increasing order. The number of features to keep to

build the model has to be determined in advance.

4.2 Justiﬁcation

In the above developements, the graph G

sim

deﬁnes a

structure between the points by connecting those pos-

sibly sharing the same clas label. Based on this struc-

ture, the matrix S

sim

(3) weights the importance of the

similarity between the samples, i.e. S

sim

i, j

will be high

if the probability that x

and x

belong to the same

class is high and will be low otherwise.

Following these considerations, a good feature f

can be seen as a feature respecting the structure de-

ﬁned by G

sim

. Indeed, intuitively, if x

and x

have the

same label with a great probability (or equivalently if

sim

i, j

is large), then it is expected that f

and f

r j

are

close (or at least closer than points having a very low

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

164

probability of belonging to the same class). Distant

features for close points in the sense of S

sim

have thus

to be penalized and not considered as relevant.

In the same way, two samples belonging to differ-

ent classes with a high probability are intuitively ex-

pected to be far from each other. Therefore, it makes

sense to penalize close features for sample points

which are distant according to S

dis

A sound criterion to assess the quality of the fea-

tures is consequently to prefer those minimizing the

following objective:

∑

( f

− f

r j

)

sim

i j

∑

( f

− f

r j

)

dis

i j

. (6)

This way, if S

sim

i, j

grows, ( f

− f

r j

)

has to be small for

the feature r to be good and the structure deﬁned by

sim

is respected. Similarly, ( f

− f

r j

)

and S

dis

i j

have

also to be high simultaneously.

In the following, we show the equivalence be-

tween expressions (5) and (6) of the WLS feature se-

lection criterion.

As already explained, the diagonal matrix D

sim

diag(S

sim

1) thus D

sim

∑

sim

i j

. Using L

sim

= D

sim

−

sim

, the graph Laplacian of G

sim

, some simple calcu-

lations give:

∑

( f

− f

r j

)

sim

i j

∑

( f

+ f

r j

− 2 f

r j

sim

i j

∑

sim

i j

∑

r j

sim

i j

− 2

∑

r j

sim

i j

= 2f

sim

− 2f

sim

= 2f

sim

− S

sim

= 2f

sim

(7)

In the same way, it is easy to prove that

∑

( f

− f

r j

)

dis

i j

= 2f

dis

It then appears clearly that minimizing (6) is equiva-

lent to minimizing (5):

min

∈X

sim

dis

= min

∈X

∑

( f

− f

r j

)

sim

i j

∑

( f

− f

r j

)

dis

i j

. (8)

Even if the scores produced by criteria (5) and (6)

are equal, it is interesting to consider both approaches.

Indeed, even if formulation (6) is more intuitive, the

use of spectral graph theory allows us to establish

connections between WLS and other feature selection

criteria such as the Fisher score (He et al., 2006).

5 EXPERIMENTAL RESULTS

This section is devoted to the presentation of exper-

imental results showing the interest of the proposed

feature selection approach, taking the uncertainty of

the class labels into account. The tests have been per-

formed on both artiﬁcial and real-world data sets for

binary and multi-class problems.

5.1 Methodology

To simulate the uncertainty of an expert and the possi-

ble errors he or she makes when labelling data points,

the following methodology has been adopted. If the

number of samples in the data set is m, m values β

are

drawn from a Beta distribution of mean µ and variance

σ = 0.1. With probability β

, the true label l

of sam-

ple x

is switched to one of the other possible labels

s6= j

, with the same probability for each label. The

probability value associated with the true class label

is set to p

i j

= 1−β

and the probability of the possibly

switched label is set to p

= β

The performances of the WLS are compared to

those obtained with two other similar strategies, both

neglecting the uncertainty of the class labels. The

ﬁrst one consists in considering as true the labels

error

(i = 1. . . m) obtained after the switch procedure

described above. The second one uses the labels

max

(i = 1 . . . m) associated with the highest probabil-

ity for each sample point.

Based on these labels, two matrices S

sim,error

(resp. S

sim,max

) and S

dis,error

(resp. S

dis,max

) are built

by setting

sim,error(max)

i, j

(

1 if y

error(max)

= y

error(max)

0 otherwise

(9)

and S

dis,error(max)

i j

= 1 − S

sim,error(max)

i j

. We again

deﬁne D

sim,error(max)

= diag(S

sim,error(max)

1) as well

as L

sim,error(max)

= D

sim,error(max)

− S

sim,error(max)

(and

similarly L

dis,error(max)

) and the score of each feature

is then computed as:

W LS

error(max)

sim,error(max)

dis,error(max)

. (10)

Equation (10) is thus the counterpart of Equation

(5) for ﬁxed labels. It is similar to the criterion

proposed for semi-supervised feature selection (Zhao

et al., 2008) and for pairwise constraints (Zhang et al.,

2008).

HANDLING IMPRECISE LABELS IN FEATURE SELECTION WITH GRAPH LAPLACIAN

165

(a) (b) (c)

Figure 1: Illustration of the three ﬁrst artiﬁcial problems; (a) Spheres, (b) Squares, (c) Circle.

5.2 Artiﬁcial Problems

The three strategies described above are ﬁrst com-

pared on ﬁve artiﬁcial data sets, for which the relevant

features are known.

The ﬁrst one is called the spheres prob-

lem. It consists in dividing the data points

into four classes corresponding to four spheres

of radius 0.25 and centered respectively in

(0.25, 0.25, 0.25), (0.25, 0.75, 0.75), (0.75, 0.75, 0.25)

and (0.75, 0.25, 0.75). A data set composed of 6

features uniformly distributed between 0 and 1 is

built; only the three ﬁrst ones, used as coordinates in

a three-dimensional space, are useful to deﬁne the

class labels. The sample size is 50.

The second problem, called squares, consists in

four classes deﬁned according to four contiguous

squares whose size length is 1. Again, 6 features uni-

formly distributed between 0 and 1 are built while

only the ﬁrst two serve as coordinates in a two-

dimensional space and are relevant to discriminate be-

tween the classes. The sample size is 100.

The third artiﬁcial problem, denoted circle, is a bi-

nary classiﬁcation one. A circle of radius 0.4 is set at

the center of a square of size length 1 and two classes

are deﬁned according to whether or not a point lies in-

side the circle. A ring of width 0.05 separates the two

classes. Only the ﬁrst two features are thus relevant in

this case; the sample size is 500. Figure 1 represents

the three ﬁrst articial problems.

The fourth and ﬁfth problems both have 10 fea-

tures f

. . . f

and a sample size of 300. The class

labels are generated by discretizing the following out-

puts:

= cos(2 f

)cos( f

)exp(2 f

) (11)

and

= 10 sin( f

)+20( f

−0.5)

+10 f

+5 f

, (12)

Table 1: Percentage of relevant features obtained by the

three feature selection techniques on the spheres data set.

µ WLS y

max

error

0.3 100 99.33 96.67

0.35 98 93.33 92

0.4 97.33 90 88.67

0.45 91.33 80 80

Table 2: Percentage of relevant features obtained by the

three feature selection techniques on the squares data set.

µ WLS y

max

error

0.35 100 98 96

0.4 99 94 96

0.45 99 93 90

0.5 96 81 78

this last problem being derived from (Friedman,

1991). More precisely, the sample points are ﬁrst

ranked in increasing value of Y

or Y

. They are then

respectively divided into three and two classes con-

taining the same number of consecutive points.

To compare the different feature selection strate-

gies, the criterion is the percentage of relevant fea-

tures among the n

best ranked features, with n

being

the total number of relevant features for a given prob-

lem. All the artiﬁcial data sets have been randomly

generated 50 times to repeat the experiments. [!ht]

Tables 1 to 5 present the results obtained with var-

Table 3: Percentage of relevant features obtained by the

three feature selection techniques on the circles data set.

µ WLS y

max

error

0.25 100 100 92

0.30 97 97 87

0.35 89 85 74

0.40 80 72 64

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

166

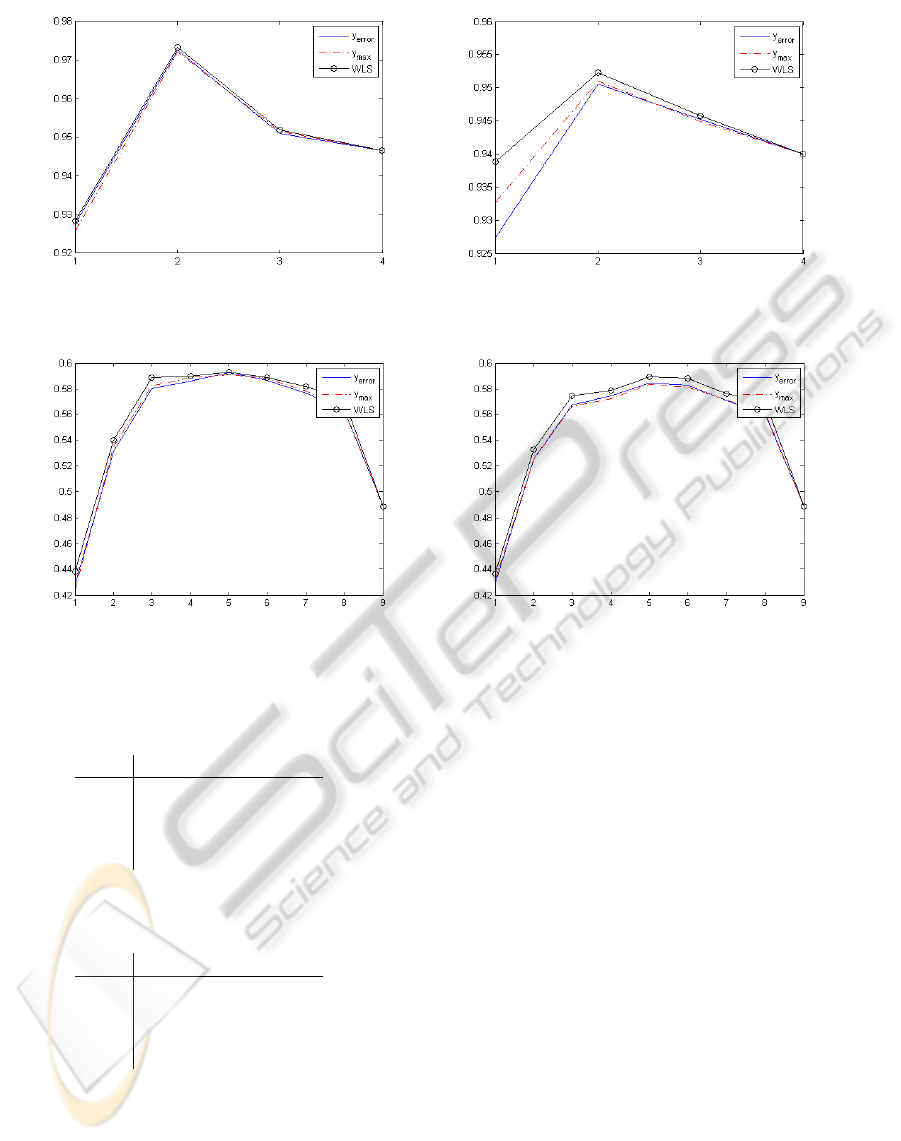
Figure 2: Accuracy of a 1NN classiﬁer as a function of the number of selected features for the Iris data set with µ = 0.2 (left)

and µ = 0.3 (right).

Figure 3: Accuracy of a 1NN classiﬁer as a function of the number of selected features for the Breast Tissue data set with

µ = 0.2 (left) and µ = 0.3 (right).

Table 4: Percentage of relevant features obtained by the

three feature selection techniques on the Y

data set.

µ WLS y

max

error

0.25 95.5 94.5 88.5

0.30 95 89 87

0.35 89.5 82.5 82

0.40 84.5 75 74

Table 5: Percentage of relevant features obtained by the

three feature selection techniques on the Y

data set.

µ WLS y

max

error

0.25 96.8 93.6 91.6

0.30 94 90 84.8

0.35 84.8 79.2 74.4

0.40 76.4 72.4 59.6

ious values of µ, depending on the complexity of the

problem. The results obtained on the ﬁve considered

artiﬁcial problems lead to very similar conclusions.

Indeed, for each problem and each value of µ, the pro-

posed WLS always outperforms its two competitors

by more accurately detecting the relevant features.

Moreover, the WLS performances are very satisfac-

tory since, for example, it selects on average more

than 90% of relevant features when µ = 0.3. This in-

dicates the adequateness of the proposed feature se-

lection strategy for problems with uncertain labels.

As could be expected, the differences in perfor-

mance between the methods are slightly smaller when

µ remains low. However, when µ is raised to more

than 25% or 30%, the advantage of considering the

uncertainty for feature selection appears clearly. As

an example, one can notice that for the spheres data

set, WLS selects 7.33% and 11.33% more relevant

features than the y

max

based strategy for respectively

µ = 35% and µ = 45%. This difference in perfor-

mances increases to 15% on the squares data set when

µ = 50%. Generally, the method based on the ob-

served class labels y

error

performs the worse.

5.3 Real-world Data Sets

To further assess the interest of the proposed feature

scoring criterion, experiments are also carried out on

three real-world data sets. The ﬁrst one is the well

known Iris data set, whose objective is to assign each

sample to one of three iris types, based on four fea-

HANDLING IMPRECISE LABELS IN FEATURE SELECTION WITH GRAPH LAPLACIAN

167

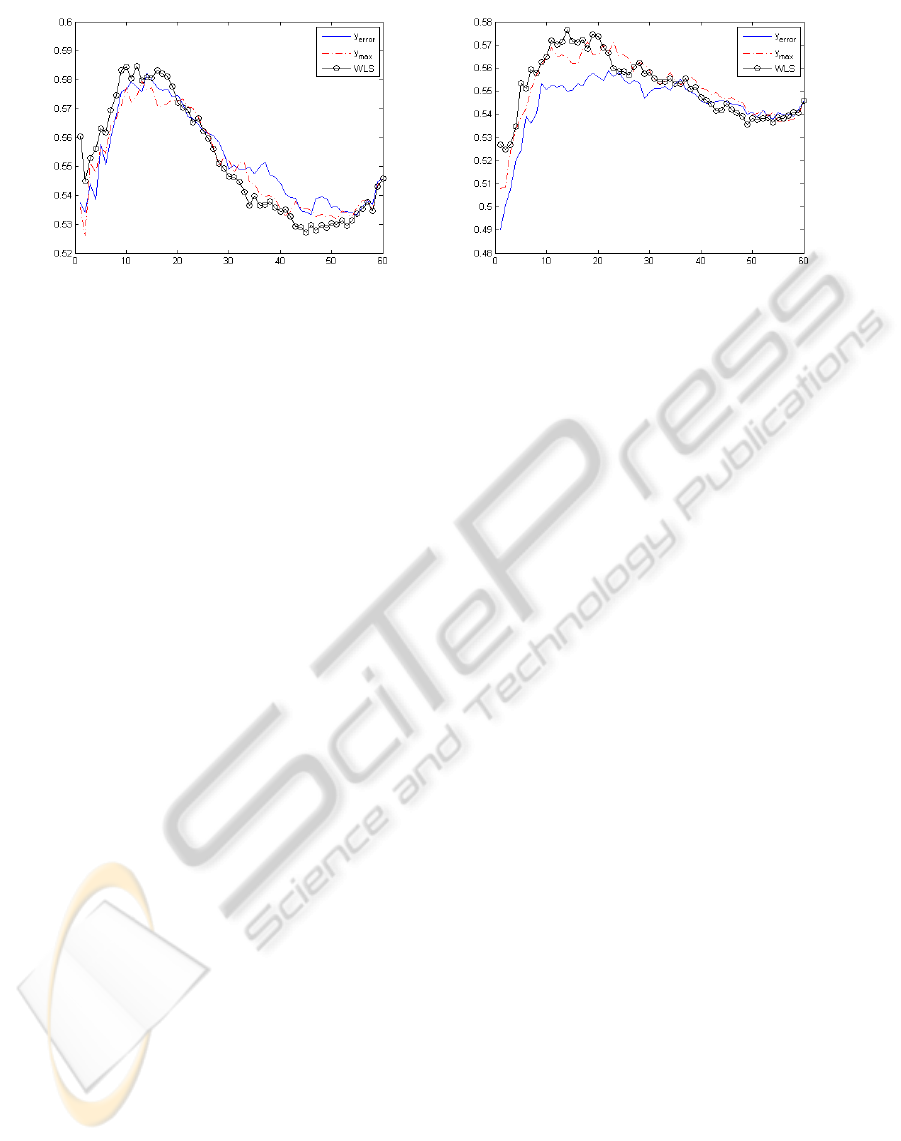
Figure 4: Accuracy of a 1NN classiﬁer as a function of the number of selected features for the Mines data set with µ = 0.2

(left) and µ = 0.3 (right).

tures. The sample size is 150. The second data set is

called Breast Tissue; it contains 106 samples and ten

features. The goal is to classify breast tissues into four

possible classes. The third data set is called Mines vs.

Rocks. The objective is to decide whether a sonar sig-

nal was bounced off by a metal cylinder (a mine) or

by a rock based on 60 features corresponding to the

energy within a particular frequency band. The sam-

ple size is 208. These three data sets can be obtained

from the UCI Machine Learning Repository website

(Asuncion and Newman, 2007).

Since the most relevant features are not known in

advance for these three data sets, the comparison cri-

terion will be the accuracy of a classiﬁer using the fea-

tures selected by the three methods. More precisely,

a 1-nearest neighbors (1NN) classiﬁer will be used,

as it is kwown to suffer dramatically from the pres-

ence of irrelevant features. The exact class labels will

be used for the classiﬁcation step while, as has been

done before, the feature selection will be achieved

with the possibly permuted labels and the expert in-

formation. This way the ability of the methods to se-

lect relevant features for the true original problem can

be compared.

Figures 2, 3 and 4 present the accuracy of the 1NN

classiﬁer as a function of the number of selected fea-

tures for µ = 20% and µ = 30%. For each data set

and each µ, the label permutation phase is randomly

repeated 50 times and the results are obtained as an

average over a ﬁve-fold cross validation procedure.

The results conﬁrm the interest of the proposed

W LS. Indeed, for the Iris and the Breast Tissue data

sets, the WLS leads to better or equal classiﬁcation

performances than its two competitors for any num-

ber of features and both contamination rates. The

differences in performance are of course larger when

µ = 30%. The Mines data set also conﬁrms that the

W LS is able to detect relevant features more quickly

than the methods which do not take label uncertainty

into account. As can be seen in Figure 4, WLS out-

perfoms the other two approaches for the ﬁrst 12 and

the ﬁrst 16 features when µ equals 20% and 30% re-

spectively. In both cases, it leads to a global best clas-

siﬁcation accuracy.

6 CONCLUSIONS

This paper proposes a way to achieve feature selec-

tion for classiﬁcation problems with imprecise labels.

More precisely, problems for which each class label

is associated with a probability value for each sample

are considered. Such problems can result from the

hesitation of an expert anotating the samples or from

the combination of several experts’ opinion; they are

likely to be encountered when a human supervision is

required to assign a class label to the points of a data

set and is thus important to consider in practice. In-

deed, such situations are frequently encountered for

medical or text categorisation problems (among oth-

ers) where errors are also possible.

The suggested methodology is based on the theory

of graph Laplacian, which received a great amount of

interest for feature selection the last few years. The

idea is to rank the features according to their ability

to preserve a neighborhood relationship deﬁned be-

tween samples. In this paper, this relationship is de-

ﬁned by computing the probabilities that two points

share the same class label. Obviously, the exact same

methodology could as well be applied for problems

where only one possible label is given with a measure

of the conﬁdence about the accuracy of this label.

Experiments on both artiﬁcial and real-world data

sets have clearly demonstrated the interest of the pro-

posed approach when compared with methods also

based on Graph laplacian that do not take the label

uncertainty into account.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

168

ACKNOWLEDGEMENTS

Gauthier Doquire is funded by a Belgian F.R.I.A.

grant.

REFERENCES

Asuncion, A. and Newman, D. (2007). UCI machine learn-

ing repository. University of California, Irvine, School

of Information and Computer Sciences, available at

http://www.ics.uci.edu/∼mlearn/MLRepository.html.

Bezdez, J. C. and Pal, S. K. (1992). Fuzzy models for pat-

tern recognition. IEEE Press, Piscataway, NJ.

Chapelle, O., Sch

olkopf, B., and Zien, A., editors (2006).

Semi-Supervised Learning. MIT Press, Cambridge,

MA.

Chung, F. R. K. (1997). Spectral Graph Theory (CBMS

Regional Conference Series in Mathematics, No. 92).

American Mathematical Society.

ome, E., Oukhellou, L., Denoeux, T., and Aknin, P.

(2009). Learning from partially supervised data using

mixture models and belief functions. Pattern Recogn.,

42:334–348.

Dash, M. and Liu, H. (1997). Feature selection for classiﬁ-

cation. Intelligent Data Analysis, 1:131–156.

Denoeux, T. and Zouhal, L. M. (2001). Handling possi-

bilistic labels in pattern classiﬁcation using evidential

reasoning. Fuzzy Sets and Systems, 122(3):47–62.

Ding, C. and Peng, H. (2003). Minimum redundancy fea-

ture selection from microarray gene expression data.

In Proceedings of the IEEE Computer Society Con-

ference on Bioinformatics, CSB ’03, pages 523–528,

Washington, DC, USA. IEEE Computer Society.

Friedman, J. H. (1991). Multivariate adaptive regression

splines. The Annals of Statistics, 19(1):1–67.

Guyon, I. and Elisseeff, A. (2003). An introduction to

variable and feature selection. J. Mach. Learn. Res.,

3:1157–1182.

Hall, M. (1999). Correlation-based Feature Selection for

Machine Learning. PhD thesis, University of Waikato.

He, X., Cai, D., and Niyogi, P. (2006). Laplacian Score

for Feature Selection. In Advances in Neural Infor-

mation Processing Systems 18, pages 507–514. MIT

Press, Cambridge, MA.

Jenhani, I., Amor, N. B., and Elouedi, Z. (2008). Decision

trees as possibilistic classiﬁers. Int. J. Approx. Rea-

soning, 48:784–807.

Kohavi, R. and John, G. H. (1997). Wrappers for Feature

Subset Selection. Artiﬁcial Intelligence, 97:273–324.

Kwak, N. and Choi, C.-H. (2002). Input feature selec-

tion for classiﬁcation problems. IEEE Transactions

on Neural Networks, 13:143–159.

Meyer, P. E., Schretter, C., and Bontempi, G. (2008).

Information-Theoretic Feature Selection in Microar-

ray Data Using Variable Complementarity. Se-

lected Topics in Signal Processing, IEEE Journal of,

2(3):261–274.

Peng, H., Long, F., and Ding, C. (2005). Feature se-

lection based on mutual information criteria of max-

dependency, max-relevance, and min-redundancy.

IEEE Transactions on Pattern Analysis and Machine

Intelligence, 27(8):1226–1238.

Semani, D., Fr

elicot, C., and Courtellemont, P. (2004).

Combinaison d’

etiquettes ﬂoues/possibilistes pour la

election de variables. In 14ieme Congr

es Franco-

phone AFRIF-AFIA de Reconnaissance des Formes et

Intelligence Artiﬁcielle, RFIA’04, pages 479–488.

Smets, P., Hsia, Y., Safﬁotti, A., Kennes, R., Xu, H.,

and Umkehren, E. (1991). The transferable belief

model. Symbolic and Quantitative Approaches to Un-

certainty, pages 91–96.

Tibshirani, R. (1996). Regression shrinkage and selection

via the lasso. Journal of the Royal Statistical Society

B, 58:267–288.

Wang, B., Jia, Y., Han, Y., and Han, W. (2009). Effective

feature selection on data with uncertain labels. In Pro-

ceedings of the 2009 IEEE International Conference

on Data Engineering, pages 1657–1662, Washington,

DC, USA.

Yang, Y. and Pedersen, J. O. (1997). A comparative study

on feature selection in text categorization. In Pro-

ceedings of the Fourteenth International Conference

on Machine Learning, ICML ’97, pages 412–420, San

Francisco, CA, USA. Morgan Kaufmann Publishers

Inc.

Yuan, M. and Lin, Y. (2006). Model selection and estima-

tion in regression with grouped variables. Journal of

the Royal Statistical Society, Series B, 68:49–67.

Zhang, D., Chen, S., and Zhou, Z.-H. (2008). Constraint

score: A new ﬁlter method for feature selection with

pairwise constraints. Pattern Recogn., 41:1440–1451.

Zhao, J., Lu, K., and He, X. (2008). Locality sensitive

semi-supervised feature selection. Neurocomputing,

71:1842–1849.

Zhao, Z. and Liu, H. (2007). Semi-supervised Feature Se-

lection via Spectral Analysis. In Proceedings of the

7th SIAM International Conference on Data Mining.

HANDLING IMPRECISE LABELS IN FEATURE SELECTION WITH GRAPH LAPLACIAN

169