DYNAMICALLY MIXING DYNAMIC LINEAR MODELS WITH

APPLICATIONS IN FINANCE

Kevin R. Keane and Jason J. Corso

Department of Computer Science and Engineering

University at Buffalo, The State University of New York, Buffalo, NY, U.S.A.

Keywords:

Bayesian inference, Dynamic linear models, Multi-process models, Statistical arbitrage.

Abstract:

Time varying model parameters offer tremendous ﬂexibility while requiring more sophisticated learning meth-

ods. We discuss on-line estimation of time varying DLM parameters by means of a dynamic mixture model

composed of constant parameter DLMs. For time series with low signal-to-noise ratios, we propose a novel

method of constructing model priors. We calculate model likelihoods by comparing forecast distributions

with observed values. We utilize computationally efﬁcient moment matching Gaussians to approximate exact

mixtures of path dependent posterior densities. The effectiveness of our approach is illustrated by extracting

insightful time varying parameters for an ETF returns model in a period spanning the 2008 ﬁnancial crisis.

We conclude by demonstrating the superior performance of time varying mixture models against constant

parameter DLMs in a statistical arbitrage application.

1 BACKGROUND

1.1 Linear Models

Linear models are utilitarian work horses in many do-

mains of application. A model’s linear relationship

between a regression vector F

and an observed re-

sponse Y

is expressed through coefﬁcients of a re-

gression parameter vector θ. Allowing an error of ﬁt

term ε

, a linear regression model takes the form:

Y = F

θ+ ε , (1)

where Y is a column vector of individual observations

, F is a matrix with column vectors F

correspond-

ing to individual regression vectors, and ε a column

vector of individual errors ε

The vector Y and the matrix F are observed. The

ordinary least squares (“OLS”) estimate

θ of the re-

gression parameter vector θ is (Johnson and Wichern,

2002):

θ =





−1

FY . (2)

1.2 Stock Returns Example

In modeling the returns of an individual stock, we

might believe that a stock’s return is roughly a linear

function of market return, industry return, and stock

speciﬁc return. This could be expressed as a linear

model in the form of (1) as follows:

r = F

θ+ ε, F =









, θ =









, (3)

where r represents the stock’s return, r

is the market

return, r

is the industry return, α is a stock speciﬁc

return component, β

is the sensitivity of the stock to

market return, and β

is the sensitivity of the stock to

it’s industry return.

1.3 Dynamic Linear Models

Ordinary least squares, as deﬁned in (2), yields a sin-

gle estimate

θ of the regression parameter vector θ

for the entire data set. Problems arise with this frame-

work if we don’t have a ﬁnite data set, but rather an in-

ﬁnite data stream. We might expect θ, the coefﬁcients

of a linear relationship, to vary slightly over time

≈θ

t+1

. This motivates the introduction of dynamic

linear models (West and Harrison, 1997). DLMs are a

generalized form, subsuming Kalman ﬁlters (Kalman

et al., 1960), ﬂexible least squares (Kalaba and Tesfat-

sion, 1996), linear dynamical systems (Minka, 1999;

Bishop, 2006), and several time series methods —

Holt’s point predictor, exponentially weighted mov-

ing averages, Brown’s exponentially weighted regres-

295

R. Keane K. and J. Corso J. (2012).

DYNAMICALLY MIXING DYNAMIC LINEAR MODELS WITH APPLICATIONS IN FINANCE.

In Proceedings of the 1st International Conference on Pattern Recognition Applications and Methods, pages 295-302

DOI: 10.5220/0003712602950302

 SciTePress

sion, and Box-Jenkins autoregressive integrated mov-

ing average models (West and Harrison, 1997). The

regime switching model in (Hamilton, 1994) may

be expressed as a DLM, specifying an autoregres-

sive model where evolution variance is zero except

at times of regime change.

1.4 Contributions and Paper Structure

The remainder of the paper is organized as follows.

In section §2, we introduce DLMs in further detail;

discuss updating estimated model parameter distri-

butions upon arrival of incremental data; show how

forecast distributions and forecast errors may be used

to evaluate candidate models; the generation of data

given a DLM speciﬁcation; inference as to which

model was the likely generator of the observed data;

and, a simple example of model inference using syn-

thetic data with known parameters. Building upon

this base, in section §3 multi-process mixture mod-

els are introduced. We report design challenges we

tackled in implementing a mixture model for ﬁnan-

cial time series. In section §4, we introduce an al-

ternative set of widely available ﬁnancial time series

permitting easier replication of the work in (Montana

et al., 2009); and we provide an example of apply-

ing a mixture model to real world ﬁnancial data, ex-

tracting insightful time varying estimates of variance

in an ETF returns model during the recent ﬁnancial

crisis. In section §5, we augment the statistical ar-

bitrage strategy proposed in (Montana et al., 2009)

by incorporating a hedge that signiﬁcantly improves

strategy performance. We demonstrate that an on-line

dynamic mixture model outperforms all statically pa-

rameterized DLMs. Further, we draw attention to the

fact that the period of unusually large mispricing iden-

tiﬁed by our mixture model coincides with unusually

high proﬁtability for the statistical arbitrage strategy.

In §6, we conclude.

2 DYNAMIC LINEAR MODELS

2.1 Specifying a DLM

In the framework of (West and Harrison, 1997), a

dynamic linear model is speciﬁed by its parameter

quadruple {F

,G,V,W}. DLMs are controlled by two

key equations. One is the observation equation:

= F

+ ν

, ν

∼ N(0,V) , (4)

the other is the evolution equation:

= Gθ

t−1

+ ω

, ω

∼ N(0,W) . (5)

Algorithm 1: Updating a DLM given G,V,W.

Initialize t = 0

{Initial information p(θ

) ∼ N[m

]}

Input: m

, C

, G, V, W

loop

t = t + 1

{Compute prior at t: p(θ

t−1

) ∼ N[a

]}

= Gm

t−1

= GC

t−1

Input: F

{Compute forecast at t: p(Y

t−1

) ∼ N[f

]}

= F

Input: Y

{Compute forecast error e

}

= Y

− f

{Compute adaptive vector A

}

= R

−1

{Compute posterior at t: p(θ

) ∼ N[m

]}

= a

+ A

= R

−A

end loop

is a row in the design matrix representing inde-

pendent variables effecting Y

. G is the evolution

matrix, capturing deterministic changes to θ, where

≈ Gθ

t−1

. V is the observational variance, Var(ε)

in ordinary least squares. W is the evolution vari-

ance matrix, capturing random changes to θ, where

= Gθ

t−1

+ w

, w

∼ N(0,W). The two parame-

ters G and W make a linear model dynamic.

2.2 Updating a DLM

The Bayesian nature of a DLM is evident in the care-

ful accounting of sources of variation that generally

increase system uncertainty; and, information in the

form of incremental observations that generally de-

crease system uncertainty. A DLM starts with initial

information, summarized by the parameters of a (fre-

quently multivariate) normal distribution:

p(θ

) ∼ N (m

) . (6)

At each time step, the information is augmented as

follows:

= {Y

t−1

} . (7)

Algorithm 1 details the relatively simple steps of

updating a DLM as additional regression vectors F

and observationsY

become available. Note that upon

arrival of the current regression vector F

, a one-step

forecast distribution p(Y

t−1

) is computed using the

prior distribution p(θ

t−1

), the regression vector F

and the observation noise V.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

296

2.3 Model Likelihood

The one-step forecast distribution facilitates compu-

tation of model likelihood by evaluation of the den-

sity of the one-step forecast distribution p(Y

t−1

)

for observation Y

. The distribution p(Y

t−1

) is ex-

plicitly a function of the previous periods informa-

tion D

t−1

; and, implicitly a function of static model

parameters {G,V,W} and model state determined by

a series of updates resulting from the history D

t−1

Deﬁning a model at time t as M

= {G,V,W, D

t−1

and explicitly displaying the M

dependency in the

one-step forecast distribution, we see that the one-

step forecast distribution is equivalent to model like-

lihood

p(Y

t−1

) = p(Y

t−1

) = p(D

) (8)

Model likelihood, p(D

), will be an important in-

put to our mixture model discussed below.

0 200 400 600 800 1000

−10

Time t

Observed Data Y

W=.05

W=5 W=.0005

DLM {1,1,1,W}

Figure 1: Observations Y

generated from a mixture of three

DLMs. Discussion appears in §2.4

2.4 Generating Observations

Before delving into mixtures of DLMs, we illustrate

the effect of varying the evolution variance W on the

state variable θ in a very simple DLM. In Figure 1

we deﬁne three very simple DLMs, {1,1,1,W

},W

∈

{.0005,.05,5}. The observations are from simple

random walks, where the level of the series θ

varies

according to an evolution equation θ

= θ

t−1

+ω

, and

the observation equation is Y

= θ

+ ν

. Compare the

relative stability in the level of observations generated

by the three models. Dramatic and interesting behav-

ior materializes as W increases.

= {Y

t−1

} by deﬁnition; M

contains

t−1

by deﬁnition; and, p(Y

t−1

) =

p(Y

t−1

)p(D

t−1

) = p(Y

t−1

0 200 400 600 800 1000

−10

Time t

W=5

W=.05

W=.0005

DLM {1,1,1,W}

Figure 2: Estimates of the mean of the state variable θ

for

three DLMs when processing generated data of Figure 1.

2.5 Model Inference

Figure 1 illustrated the differencein appearance of ob-

servations Y

generated with different DLM parame-

ters. In Figure 2, note that models with smaller evo-

lution variance W result in smoother estimates — at

the expense of a delay in responding to changes in

level. At the other end of the spectrum, large W per-

mits rapid changes in estimates of θ — at the ex-

pense of smoothness. In terms of the model likeli-

hood p(D

), if W is too small, the standardized

forecast errors e

√

will be large in magnitude, and

therefore model likelihood will be low. At the other

extreme, if W is too large, the standardized forecast

errors will appear small, but the model likelihood will

be low now due to the diffuse forecast distribution.

In Figure 3, we graph the trailing interval log like-

lihoods for each of the three DLMs. We deﬁne trailing

interval (k-period) likelihood as:

(k) = p(Y

t−1

,...,Y

t−k+1

t−k

)

= p(Y

t−1

)p(Y

t−1

t−2

)...

p(Y

t−k+1

t−k

) .

(9)

This concept is very similar to Bayes’ factors dis-

cussed in (West and Harrison, 1997), although we

do not divide by the likelihood of an alternative

model. Our trailing interval likelihood is also simi-

lar to the likelihood function discussed in (Crassidis

and Cheng, 2007); but, we assume the errors e

are

not autocorrelated.

Across the top of Figure 3 appears a color code

indicating the true model prevailing at time t. It is

interesting to note when the likelihood of a model ex-

ceeds that of the true model. For instance, around the

t = 375 mark, the model with the smallest evolution

variance appears most likely. Reviewing Figure 2,

the state estimates of DLM {1,1,1,W = .0005} just

DYNAMICALLY MIXING DYNAMIC LINEAR MODELS WITH APPLICATIONS IN FINANCE

297

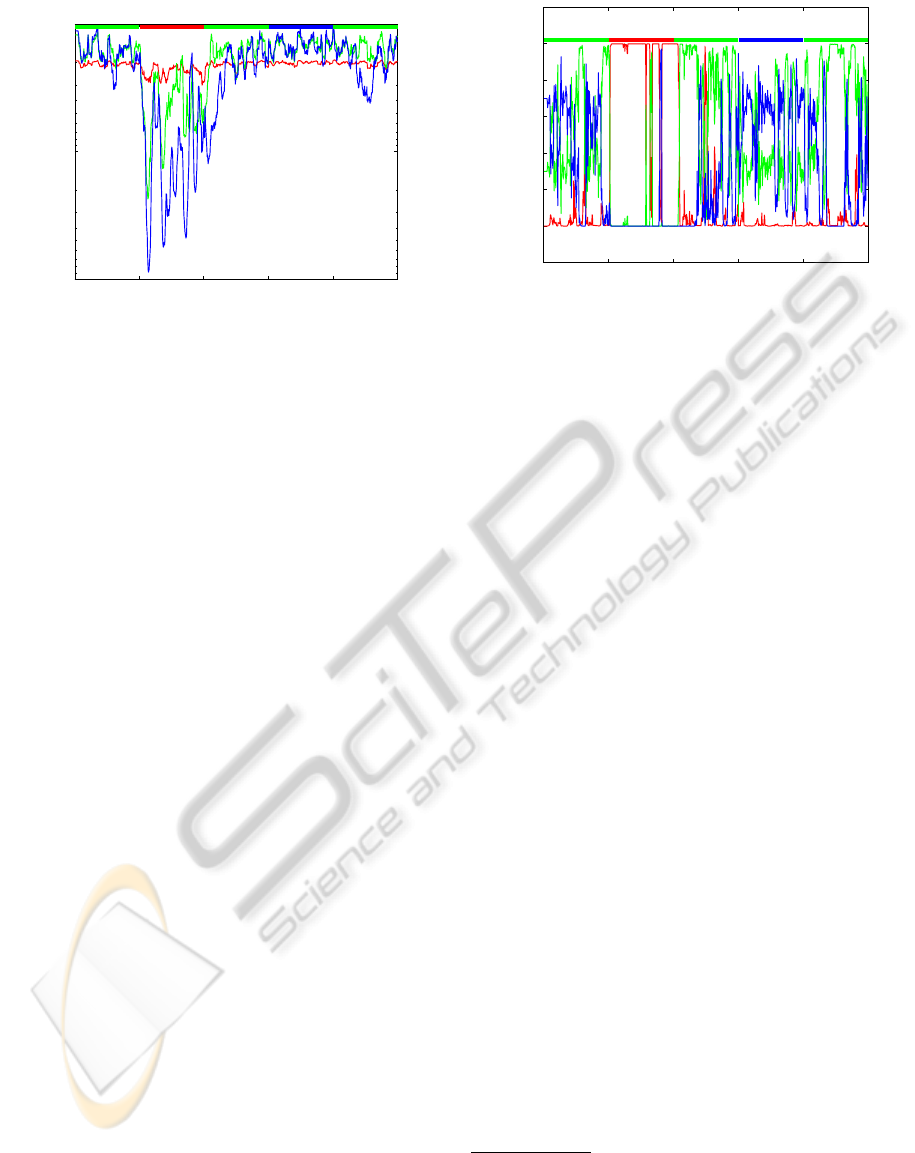
0 200 400 600 800 1000

−10

Time t

10−day log likelihood

W=5 W=.05 W=.0005

Figure 3: Log likelihood of observed data during most re-

cent 10 days given the parameters of three DLMs when pro-

cessing generated data of Figure 1. Bold band at top of ﬁg-

ure indicates the true generating DLM.

happened to be in the right place at the right time.

Due to the more concentrated forecast distributions

p(Y

t−1

) of this model, it brieﬂy attains the high-

est trailing 10-period log likelihood. A similar oc-

currence can be seen for the DLM {1, 1,1,W = .05}

around t = 325.

While the series on Figure 3 appear visually close

at times, note the log scale. After converting back to

normalized model probabilities, the favored model at

a particular instance is more apparent as illustrated in

Figure 4. In §5, we will perform model inference on

the return series of exchange traded funds (ETFs).

3 PARAMETER ESTIMATION

In §2, we casually discussed DLMs varying in pa-

rameterization. Generating observations from a spec-

iﬁed DLM or combination of DLMs, as in §2.4, is

trivial. The inverse problem, determining model pa-

rameters from observations is signiﬁcantly more chal-

lenging. There are two distinct versions of this task

based upon area of application. In the simpler case,

the parameters are unknown but assumed constant. A

number of methods are available for model identiﬁ-

cation in this case, both off-line and on-line. For ex-

ample, (Ghahramani and Hinton, 1996) use E-M off-

line, and (Crassidis and Cheng, 2007) use the likeli-

hood of a ﬁxed-length trailing window of prediction

errors on-line. Time varying parameters are signiﬁ-

cantly more challenging. The posterior distributions

are path dependent and the number of paths is expo-

nential in the length of the time series. Various ap-

proaches are invoked to obtain approximate solutions

with reasonable computational effort. (West and Har-

0 200 400 600 800 1000

−0.2

0.2

0.4

0.6

0.8

Time t

P( M | D )

W=5 W=.05 W=.0005

Figure 4: Model probabilities from normalized likelihoods

of observed data during most recent 10 periods. Bold band

at top of ﬁgure indicates the true generating DLM.

rison, 1997) approximate the posterior with a single

Gaussian that matches the moments of the exact dis-

tribution. (Valpola et al., 2004; Sarkka and Nummen-

maa, 2009) propose variational Bayesian approxima-

tion. (Minka, T.P., 2007) discusses Gaussian-sum and

assumed-density ﬁlters.

3.1 Multi-process Mixture Models

(West and Harrison, 1997) deﬁne sets of DLMs,

where the deﬁning parameters M

= {F, G,V,W}

are

indexed by λ

, so that M

= M(λ

). The set of DLMs

at time t is {M(λ

) : λ

∈ Λ}. Two types of multi-

process models are deﬁned. A class I multi-process

model, where for some unknown λ

∈Λ,M(λ

) holds

for all t; and, a class II multi-process model for some

unknown sequence λ

∈ Λ,(t = 1, 2,...),M(λ

) holds

at time t. We build our model in §4 in the framework

of a class II mixture model. We do not expect to be

able to specify parameters exactly or ﬁnitely. Instead,

we specify a set of models that quantize a range of

values. In the terminology of (Sarkka and Nummen-

maa, 2009), we will create a grid approximation to

the evolution and observation variance distributions.

Class II mixture models permit the speciﬁcation

of a model per time period, leading to a number of

potential model sequences exponential in the steps,

|Λ|

. However, in the spirit of the localized nature of

dynamic models and practicality, (West and Harrison,

1997) exploit the fact that the value of information

decreases quickly with time, and propose collapsing

(West and Harrison, 1997) index the set of component

models α ∈ A ; however, by convention in ﬁnance, α refers

to stock speciﬁc return, consistent with §1.2. To avoid con-

fusion, we index the set of component models λ ∈ Λ, con-

sistent with the notation of (Chen and Liu, 2000).

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

298

the paths and approximating common posterior dis-

tributions. In the ﬁltering literature, this technique is

referred to as the interacting multiple model (IMM)

estimator (Bar-Shalom et al., 2001, Ch. 11.6.6). In

our application, in §5, we limit our sequences to two

steps, and approximate common posterior distribu-

tions by collapsing individual paths based on the most

recent two component models. To restate this brieﬂy,

we model two step sequences — the component

model M

t−1

just exited, and the component model M

now occupied. Thus, we consider |Λ|

sequences. Re-

viewing Algorithm 1, the only information required

from t −1 is captured in the collapsed approximate

posterior distribution p(θ

t−1

) ∼ N (m

t−1

)

for each component model λ

t−1

∈ Λ considered.

3.2 Specifying Model Priors

One key input to mixture models are the model pri-

ors. We have tried several approaches to this task

before ﬁnding a method suitable for our statistical

arbitrage modeling task in §5. The goal of our en-

tire modeling process is to design a set of model

priors p(M(λ

)) and model likelihoods p(D|M(λ

))

that yield in combination insightful model posterior

distributions p(M(λ

)|D), permitting the computation

of quantities of interest by summing over the model

space λ

∈ Λ at time t:

p(X

) ∝

∑

∈Λ

p(X

|M(λ

))p(M(λ

)|D

) (10)

In the context of modeling ETF returns discussed

in §5, the vastly different scales for the contribu-

tion of W and V to Q left our model likelihoods un-

responsive to values of W. This unresponsiveness

was due to the fact that parameter values W and V

are of similar scale; however, a typical |F

| for this

model is approximately 0.01, and therefore the re-

spective contributions to the forecast variance Q =

RF +V = F

(GCG

+ W)F + V are of vastly dif-

ferent scales, 1 : 10,000. Speciﬁcally, density of the

likelihood p(Y

t−1

) ∼ N(f

) is practically con-

stant for varying W after the scaling by 0.01

. The

only knob left for us to twist is that of the model pri-

ors.

DLMs with static parameters embed evidence of

recent model relevance in their one-step forecast dis-

tributions. In contrast, mixture model component

DLMs move forward in time from posterior distribu-

tions that mask model performance. The situation is

similar to the game best ball in golf. After each player

hits the ball, all players’ balls are moved to a best po-

sition as a group. Analogously, when collapsing pos-

terior distributions, sequences originating from differ-

ent paths are approximated with a common posterior

based upon end-point model. While some of us may

appreciate obfuscation of our golf skills, the obfus-

cation of model performance is problematic. Due to

the variance scaling issues of our application, the path

collapsing, common posterior density approximating

technique destroys the accumulation of evidence in

one-step forecast distributions for speciﬁc DLM pa-

rameterizations λ ∈ Λ. In our current implementa-

tion, we retain local evidence of model effectiveness

by running a parallel set of standalone (not mixed)

DLMs. Thus, the total number of models maintained

is |Λ|

+ |Λ|, and the computational complexity re-

mains asymptotically constant. In our mixture model,

we deﬁne model priors proportional to trailing in-

terval likelihoods from the standalone DLMs. This

methodology locally preserves evidence for individ-

ual models as shown in Figure 3 and Figure 4.

The posterior distributions p(θ

)

M(λ)

emitted

by identically parameterized standalone and compo-

nent DLMs differ in general. A standalone constant

parameter DLM computes the prior p(θ

t−1

)

M(λ

)

as outlined in Algorithm 1 using its own poste-

rior p(θ

t−1

)

M(λ

=λ

t−1

)

. In contrast, component

DLMs compute prior distributions using a weighted

posterior:

p(θ

t−1

)

M(λ

)

∑

t−1

p(M(λ

t−1

)|M(λ

))p(θ

t−1

)

M(λ

t−1

)

(11)

4 A FINANCIAL EXAMPLE

(Montana et al., 2009) proposed a model for the re-

turns of the S&P 500 Index based upon the largest

principal component of the underlying stock returns.

In the form Y = F

θ+ ε used throughout this paper,

Y = r

s&p

, F = r

pc1

, and θ = β

pc1

. (12)

The target and explanatory data in (Montana et al.,

2009) spanned January 1997 to October 2005. We

propose the use of two alternative price series that are

very similar in nature; but, publicly available, widely

disseminated, and tradeable. The proposed alterna-

tive to the S&P Index is the SPDR S&P 500 ETF

(trading symbol SPY). SPY is an ETF designed to

mimic the performance of the S&P 500 Index(PDR

Services LLC, 2010). The proposed alternative to the

largest principal component series is the Rydex S&P

Equal Weight ETF (trading symbol RSP). RSP is an

ETF designed to mimic the performance of the S&P

Equal Weight Index (Rydex Distributors, LLC, 2010).

While perhaps not as obvious a pairing as S&P Index /

DYNAMICALLY MIXING DYNAMIC LINEAR MODELS WITH APPLICATIONS IN FINANCE

299

2004 2006 2008 2010

100

150

200

250

Price

Date

RSP

SPY

Figure 5: SPDR S&P 500 (SPY) and Rydex S&P Equal

Weight (RSP) ETF closing prices, scaled to April 30, 2003

= 100.

SPY, a ﬁrst principal component typically is the mean

of the data — in our context, the mean is the equal

weighted returns of the stocks underlying the S&P

500 Index. SPY began trading at the end of January

1993. RSP began trading at the end of April 2003.

We use the daily closing prices P

to compute daily

log returns:

= log



t−1



. (13)

Our analysis is based on the months during which

both ETFs traded, May 2003 to present (August

2011).

The price levels, scaled to 100 on April 30, 2003

are shown in Figure 5. Visually assessing the price

series, it appears the two ETFs have common direc-

tions of movement, with RSP displaying somewhat

greater range than SPY. Paralleling the work of (Mon-

tana et al., 2009), we will model the return of SPY as

a linear function of RSP, Y = F

θ+ ε:

Y = r

spy

, F = r

rsp

, and θ = β

rsp

. (14)

We estimate the time varying regression parameter

using a class II mixture model composed of 50 can-

didate models with parameters {F

,1,V,W}. F

= r

rsp

the return of RSP, is common to all models. The

observation variances are the values V ×1,000, 000 ∈

{1, 2.15, 4.64, 10, 21.5, 46.4, 100, 215, 464, 1,000 }.

The evolution variances are the values

W × 1,000,000 ∈ { 10, 56, 320, 1,800, 10, 000 }.

Our on-line process computes 50

+ 50 = 2550

DLMs, 50

DLMs corresponding to the two-period

model sequences, and 50 standalone DLMs required

for trailing interval likelihoods. In the mixture

model, the priors p(M(λ

)) for component models

M(λ

), λ

∈ Λ, are proportional to trailing inter-

val likelihoods (9) of corresponding identically

parameterized standalone DLMs.

It’s an interesting side topic to consider the po-

tential scale of these mixtures. Circa 1989, in the

2004 2006 2008 2010

0.001

0.010

0.100

Std dev / day

Date

sqrt(V)

sqrt(W)

Figure 6: The daily standard deviation of ν

and ω

estimated by the mixture model. Observation noise ν

∼

N(0,V); evolution noise ω

∼ N(0,W).

predecessor text to (West and Harrison, 1997), West

and Harrison suggested the use of mixtures be re-

stricted for purposes of “computational economy”;

and that a single DLM would frequently be adequate.

Approximately one decade later, (Yelland and Lee,

2003) were running a production forecasting system

with 100 component models, and 10,000 model se-

quence combinations. Now, more than two decades

after West and Harrison’s practical recommendation,

with the advent of ubiquitous inexpensive GPGPUs,

the economics of computation have changed dramat-

ically. A direction of future research is to revisit im-

plementation of large scale mixture models quantiz-

ing several dimensions simultaneously.

Subsequent to running the mixture model for the

period May 2003 to present, we are able to review es-

timated time varying parameters V

and W

, as shown

in Figure 6. This graph displays the standard devia-

tion of observation and evolution noise, commonly re-

ferred to as volatility in the ﬁnancial world. It is inter-

esting to review the decomposition of this volatility.

Whereas the relatively stationary series

√

W in Fig-

ure 6 suggests the rate of evolution of θ

is fairly con-

stant across time; the observation variance V varies

dramatically, rising noticeably during periods of ﬁ-

nancial stress in 2008 and 2009. The observation vari-

ance, or standard deviation as shown, may be inter-

preted as the end-of-day mispricing of SPY relative

to RSP. In §5, we will demonstrate a trading strategy

taking advantage of this mispricing. The increased

observational variance at the end of 2008, visible in

Figure 6 results in an increase in the rate of proﬁtabil-

ity of the statistical arbitrage application plainly visi-

ble in Figure 7.

5 STATISTICAL ARBITRAGE

(Montana et al., 2009) describe an illustrative statis-

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

300

2004 2006 2008 2010

100

% Return

Date

Best DLM {F,1,1,W=221}

DLMs {F,1,1,W}

Mixture Model

Figure 7: Cumulative return of the various implementations

of a statistical arbitrage strategy based upon a time varying

mixture model and 10 constant parameter DLMs.

tical arbitrage strategy. Their proposed strategy takes

equal value trading positions opposite the sign of the

most recently observed forecast error ε

t−1

. In the ter-

minology of this paper, they tested 11 constant param-

eter DLMs, with a parameterization variable δ equiv-

alent to:

δ =

W +V

. (15)

They note that this parameterization variable δ per-

mits easy interpretation. With δ ≈ 0, results ap-

proach an ordinary least squares solution: W = 0 im-

plies θ

= θ. Alternatively, as δ moves from 0 towards

1, θ

is increasingly permitted to vary.

Figure 6 challenges the concept that a constant

speciﬁcation of evolution and observation variance

is appropriate for an ETF returns models. To ex-

plore the effectiveness of class II mixture models

versus statically parameterized DLMs, we evalu-

ated the performance of our mixture model against

10 constant parameter DLMs. We set V = 1 as

did (Montana et al., 2009), and speciﬁed W ∈

{29, 61,86,109,139, 179,221,280,412, 739}. These

values correspond to the 5, 15, ...95%-tile values of

W/V observed in our mixture model.

Figure 6 offers no justiﬁcation of using V = 1.

While the prior p(θ

t−1

), one-step p(Y

t−1

) and

posterior p(θ

) “distributions” emitted by these

DLMs will not be meaningful, the intent of such a

formulation is to provide time varying point estimates

of the state vector θ

. The distribution of θ

is not

of interest to modelers applying this approach. In the

context of the statistical arbitrage application consid-

ered here, the distribution is not required. The trading

rule proposed is based on the sign of the forecast er-

ror; and, the forecast is a function of the prior mean a

(a point estimate) for the state vector θ

and observed

values F

and Y

: ε

= Y

−F

10 100

2.0

2.5

3.0

Sharpe ratio

Evolution Variance W

DLMs {F,1,1,W}

Mixture Model

Figure 8: Sharpe ratios realized by the time varying mixture

model and 10 constant parameter DLMs.

5.1 The Trading Strategy

Consistent with (Montana et al., 2009), we ignore

trading and ﬁnancing costs in this simpliﬁed experi-

ment. Given the setup of constant absolute value SPY

positions taken daily, we compute cumulative returns

by summing the daily returns. The rule we implement

is:

portfolio

(ε

t−1

) =

(

+1 if ε

t−1

≤ 0,

−1 if ε

t−1

> 0.

(16)

where

portfolio

= +1 denotes a long SPY and

short RSP position;

portfolio

= −1 denotes a short

SPY and long RSP position. The SPY leg of the trade

is of constant magnitude. The RSP leg is −a

× SPY-

value, where a

is the mean of the prior distribution of

, p(θ

t−1

) ∼ N(a

); and, recall from (14) the

interpretation of θ

is the sensitivity of the returns of

SPY Y

to the returns of RSP F

. Note that this strat-

egy is a modiﬁcation to (Montana et al., 2009) in that

we hedge the S&P exposure with the equal weighted

ETF, attempting to capture mispricings while elimi-

nating market exposure. The realized Sharpe ratios

appear dramatically higher in all cases than in (Mon-

tana et al., 2009), primarily attributable to the hedging

of market exposure in our variant of a simpliﬁed arbi-

trage example. Montana et al. report Sharpe ratios in

the 0.4 - 0.8 range; in this paper, after inclusion of the

hedging technique, Sharpe ratios are in the 2.3 - 2.6

range.

5.2 Analysis of Results

We reiterate that we did not include transaction costs

in this simple example. Had we done so, the results

would be signiﬁcantly diminished. With that said, we

will review the relative performance of the models for

the trading application.

In Figure 7, it is striking that all models do fairly

DYNAMICALLY MIXING DYNAMIC LINEAR MODELS WITH APPLICATIONS IN FINANCE

301

well. The strategy holds positions based upon a com-

parison of the returns of two ETFs, one scaled by

an estimate of β

rsp

. Apparently small variation in

the estimates of the regression parameter are not of

large consequence. Given the trading rule is based

on the sign of the error ε

, it appears that on many

days, slight variation in the estimate of θ

across

DLMs does not result in a change to

sign

(ε

). Fig-

ure 8 shows that over the interval studied, the mixture

model provided a higher return per unit of risk, if only

to a modest extent. What is worth mentioning is that

the comparison we make is the on-line mixture model

against the ex post best performance of all constant

parameter models. Acknowledging this distinction,

the mixture model’s performance is more impressive.

6 CONCLUSIONS

Mixtures of dynamic linear models are a useful tech-

nology for modeling time series data. We show the

ability of DLMs parameterized with time varying val-

ues to generate observations for complex dynamic

processes. Using a mixture of DLMs, we extract time

varying parameter estimates that offered insight to the

returns process of the S&P 500 ETF during the ﬁnan-

cial crisis of 2008. Our on-line mixture model demon-

strated superior performance compared to the ex post

optimal component DLM in a statistical arbitrage ap-

plication.

The contributions of this paper include the pro-

posal of a method, trailing interval likelihood, for

constructing component model prior probabilities.

This technique facilitated successful modeling of time

varying observational and evolution variance parame-

ters, and captured model evidence not adequately con-

veyed in the one-step forecast distribution due to scal-

ing issues. We proposed the use of two widely avail-

able time-series to facilitate easier replication and

extension of the statistical arbitrage application pro-

posed by (Montana et al., 2009). Our addition of

a hedge to the statistical arbitrage application from

(Montana et al., 2009) resulted in dramatically im-

proved Sharpe ratios.

We have only scratched the surface of the mod-

eling possibilities with DLMs. The mixture model

technique eliminates the burden of a priori speciﬁca-

tion of process parameters. We look forward to evalu-

ating models with higher dimension state vectors and

parameterized evolution matrices. Due to the inher-

ently parallel nature of DLM mixtures, we also look

forward to exploring the ability of current hardware

to tackle additional challenging modeling problems.

REFERENCES

Bar-Shalom, Y., Li, X., Kirubarajan, T., and Wiley, J.

(2001). Estimation with applications to tracking and

navigation. John Wiley & Sons, Inc.

Bishop, C. (2006). Pattern Recognition and Ma-

chine Learning (Information Science and Statistics).

Springer Science+Business Media, LLC. New York,

NY, USA.

Chen, R. and Liu, J. (2000). Mixture Kalman ﬁlters. Jour-

nal of the Royal Statistical Society: Series B (Statisti-

cal Methodology), 62(3):493–508.

Crassidis, J. and Cheng, Y. (2007). Generalized Multiple-

Model Adaptive Estimation Using an Autocorrelation

Approach. In Information Fusion, 2006 9th Interna-

tional Conference on, pages 1–8. IEEE.

Ghahramani, Z. and Hinton, G. (1996). Parameter estima-

tion for linear dynamical systems. Technical Report

CRG-TR-96-2, University of Toronto.

Hamilton, J. (1994). Time series analysis. Princeton Uni-

versity Press: Princeton, NJ, USA.

Johnson, R. and Wichern, D. (2002). Applied Multivari-

ate Statistical Analysis. Prentice Hall: Upper Saddle

River, NJ, USA.

Kalaba, R. and Tesfatsion, L. (1996). A multicriteria ap-

proach to model speciﬁcation and estimation. Com-

putational Statistics & Data Analysis, 21(2):193–214.

Kalman, R. et al. (1960). A new approach to linear ﬁltering

and prediction problems. Journal of Basic Engineer-

ing, 82(1):35–45.

Minka, T. (1999). From hidden Markov models to linear

dynamical systems. Technical Report 531, Vision and

Modeling Group of Media Lab, MIT.

Minka, T.P. (2007). Bayesian inference in dynamic models:

an overview. http://research.microsoft.com.

Montana, G., Triantafyllopoulos, K., and Tsagaris, T.

(2009). Flexible least squares for temporal data min-

ing and statistical arbitrage. Expert Systems with Ap-

plications, 36(2):2819–2830.

PDR Services LLC (2010). Prospectus. SPDR S&P 500

ETF. https://www.spdrs.com.

Rydex Distributors, LLC (2010). Prospectus. Rydex S&P

Equal Weight ETF. http://www.rydex-sgi.com/.

Sarkka, S. and Nummenmaa, A. (2009). Recursive noise

adaptive Kalman ﬁltering by variational Bayesian ap-

proximations. Automatic Control, IEEE Transactions

on, 54(3):596–600.

Valpola, H., Harva, M., and Karhunen, J. (2004). Hierar-

chical models of variance sources. Signal Processing,

84(2):267–282.

West, M. and Harrison, J. (1997). Bayesian Forecasting

and Dynamic Models. Springer-Verlag New York, Inc.

New York, NY, USA.

Yelland, P. and Lee, E. (2003). Forecasting product sales

with dynamic linear mixture models. Technical Re-

port SMLI TR-2003-122, Sun Microsystems, Inc.

ICPRAM 2012 - International Conference on Pattern Recognition Applications and Methods

302