SYMMETRY BREAKING CONSTRAINTS FOR THE PROBLEM OF

PACKING EQUAL CIRCLES IN A SQUARE

Alberto Costa

and Ider Tseveendorj

LIX,

Ecole Polytechnique, 91128 Palaiseau, France

PRISM, Universit

e de Versailles Saint Quentin en Yvelines, 78035 Versailles, France

Keywords:

Symmetry breaking constraints, Packing of equal circles, Reformulation, Narrowing, Nonconvex NLP.

Abstract:

The Packing Equal Circles in a Square (PECS) problem is a nonconvex nonlinear optimization problem which

involves a high degree of symmetry. The Branch-and-Bound algorithms work bad due to the presence of

symmetric optima, because the Branch-and-Bound tree becomes large, and the time to reach the leaves (i.e.,

the optimal solutions) increases. In this paper, we introduce some inequalities which reduce the symmetry of

the problem, and we present some numerical results.

1 INTRODUCTION

Circle Packing in a Square is a well-known problem

in mathematics. There exist different but equivalent

mathematical formulations for it: if an optimum for

one of these is known, then we can easily ﬁnd the op-

timal solutions for the others. In (Szab

o et al., 2007)

there is a detailed description of the relationships be-

tween the existing formulations.

Among the most known settings for this problem,

we have the followings:

• Find the maximum common radius r for n non-

overlapping circles arranged in the unit square; we

refer to this description as Packing Equal Circle in

a Square (PECS);

• Place n points in the unit square such that the min-

imum pairwise distance is maximal; this problem

will be addressed as Point Packing in a Square

(PPS).

The previous descriptions represent some exam-

ples of the optimization version of the problem; there

exists also the decision version, like the following:

Given L and n, can n non-overlapping circles

of radius 1 be arranged in a square of side L ?

This problem is hard to solve by Branch-and-

Bound algorithms for two main reasons: ﬁrst, more

than one optimal solution is possible, and the presence

of symmetric optima makes the search process longer.

Second, it is a nonlinear nonconvex problem. How-

ever, we chose to use the PECS formulation, since

some experiments showed it is easier to solve in prac-

tice.

1.1 Related Works

In the literature several techniques were proposed

to solve Circle Packing in a Square. One of the

approaches is to use geometrical properties of the

optimal solutions to derive a particular Branch-and-

Bound algorithm (Locatelli and Raber, 2002); another

Branch-and-Bound based technique uses the interval

arithmetics instead (Szab

o et al., 2007).

However, it should be remarked that most of the

existing approaches are heuristics. In the billiard

simulation method (Graham and Lubachevsky, 1996),

each circle is a ball with radius, speed and direction;

then the radius is increased while the structure of the

packing becomes ﬁx. A similar idea is used in the

Pulsating Disk Shaking (PSD) algorithm (Szab

o et al.,

2007).

TAMSASS-PECS algorithm combines both the

Threshold Accepting method (TA) (where, as in the

Simulated Annealing, a new solution is accepted if it

decreases the quality of the current solution less than

a given threshold), and a modiﬁed version of SASS

(Single Agent Stochastic Search) for the PECS prob-

lem (Casado et al., 2001; Szab

o et al., 2007).

The perturbation method tries to ﬁnd good solu-

tions for PPS by moving the points in the square up,

down, left or right; how much we can move the points

is determined by a parameter, and its value decreases

during the process. After that, the position of a point

Costa A. and Tseveendorj I..

SYMMETRY BREAKING CONSTRAINTS FOR THE PROBLEM OF PACKING EQUAL CIRCLES IN A SQUARE.

DOI: 10.5220/0003713100050010

In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 5-10

ISBN: 978-989-8425-97-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

is updated if the distance between the point and the

neighbours increases (Boll et al., 2000).

Another approach to solve PPS, which is related

to a physical interpretation of the problem, is the min-

imization of an energy function (Szab

o et al., 2007).

The points are viewed as electrical charges repulsing

each others: if the distance between two points in-

creases, the energy decreases. A similar approach was

used also in (Nurmela and

Osterg

ard, 1997).

It is also possible to describe the structure of the

optimal packing by means of a quadratical system

of equations. After some manipulation, the problem

can be reformulated as the solution of a polynomial,

where the smallest positive root is the optimal solu-

tion for PPS (Szab

o, 2005; Szab

o et al., 2007).

A different way to solve the problem consists

in trying to predict the structure of optimal pack-

ings. It was noticed that in the optimal solutions

there are some repeated patterns, thus it was possi-

ble to divide some packings into classes (Graham and

Lubachevsky, 1996; Nurmela and

Osterg

ard, 1997).

Even if not all the packings belong to one of the

known pattern classes, it is very likely that not all

classes has been discovered yet.

1.2 Effect of Symmetries in the

Mathematical Programming

Approach

In this paper, we do not propose a new speciﬁc algo-

rithm to solve PECS. We try to describe it as a math-

ematical programming problem, and to solve it with

general Mixed-Integer Nonlinear Program (MINLP)

solvers as COUENNE (Belotti et al., 2009) or BARON

(Sahinidis and Tawarmalani, 2005), which implement

the spatial Branch-and-Bound (sBB) algorithm, based

on a search tree; in fact, sBB can be used to obtain

an ε-approximation for general nonconvex NLPs and

MINLPs (Belotti et al., 2009; Liberti, 2006; Smith

and Pantelides, 1999).

When we try to solve PECS by using sBB algo-

rithms, we do not obtain good results: in fact, the

presence of several symmetric solutions makes the

BB tree very large, so the time to reach the leaves

(which represent the optimal solutions) becomes very

high.

We can characterize the symmetries of PECS by

means of the so called formulation group G

: it is

a subgroup of the permutations on the variables of

a problem P which maps optimal solutions in other

optimal solutions, and it is possible to calculate it

by looking at the formulation of the problem, as ex-

plained in (Costa et al., 2010a; Liberti, 2010). In

particular, the following theorem is proved in (Costa

et al., 2010a) (it is actually proved for the decision

version of Circle Packing, but the proof is almost the

same for PECS):

Theorem 1.1. The formulation group of Circle Pack-

ing in a Square is isomorphic to C

x S

Here, C

(the cyclic group of order 2) refers to

swapping x and y axes and S

(the symmetric group of

order n) refers to reindexing the circles in an arbitrary

way.

In order to break these symmetries, we add some

Symmetry Breaking Constraints (SBCs) to the origi-

nal formulation (Liberti, 2008; Liberti, 2010). Recall

that a set of constraints h(x) ≤ 0 are SBCs with re-

spect to π ∈ G

if there is an optimal solution y such

that h(πy) ≤ 0. Adjoining SBCs to a problem P yields

a narrowing Q of P: this means that in Q some sym-

metric optima of P become infeasible, but at least one

is kept (Liberti, 2009).

In (Costa et al., 2010a) some classes of SBCs were

proposed, and the better results were obtained after

adding a set of order constraints on the variables, that

≤ x

i+1

, ∀i < n. (1)

These constraints are called strong in (Costa et al.,

2010a). However, it should be underlined that not all

the symmetric optima are eliminated by constraints

(1): that is the reason of our investigation for other

SBCs.

The rest of the paper is organized as follows: in

Section 2 we introduce more formally the PECS; in

Section 3 we present some new constraints for this

problem. In Section 4 we show some numerical re-

sults, and at the end in Section 5 there are the conclu-

sions and future work.

2 PACKING EQUAL CIRCLES IN

A SQUARE

The PECS problem can be described in this way:

maxr (2)

∀i < j ≤ n (x

− x

)

+ (y

− y

)

≥ 4r

(3)

∀i ≤ n x

≤ 1 − r (4)

∀i ≤ n y

≤ 1 − r (5)

∀i ≤ n x

≥ r (6)

∀i ≤ n y

≥ r (7)

r ≥ 0 (8)

∀i < n x

≤ x

i+1

. (9)

The positive variable r is the radius we want to max-

imize, while x

, y

are the coordinates of the center of

the circle i.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

Inequalities (3) represent the non-overlapping

conditions, and they are also the responsible for the

complexity of this problem (since they are nonlinear

and nonconvex), while conditions (4)-(7) mean that

the circles are inside the square. Constraints (9) are

the order inequalities (1) presented at the end of Sec-

tion 1.2.

3 NEW CONSTRAINTS FOR

PECS

In order to make infeasible more symmetric solutions

we introduce two other classes of SBCs in Sections

3.1 and 3.2. Furthermore, in Section 3.3 we propose

another class of inequalities which strengthen the for-

mulation.

3.1 Fixing Points Constraints

In (Locatelli and Raber, 2002), the authors present

the following theorem for PPS (proof can be found

in (Locatelli and Raber, 1999; Raber, 1999)):

Theorem 3.1. There always exists an optimal solu-

tion of problem PPS such that at each vertex v of the

unit square, formed by the edges e

and e

, one and

only one of the following statements holds:

• a point of the optimal solution is in the vertex v;

• two points of the optimal solution belong to the

edges e

and e

and have distance equal to the

optimal one.

Starting from this theorem, and calling point a

center of a circle, we can prove the following:

Theorem 3.2. Consider the PECS with n ≥ 4. There

is always an optimal solution where at least two

points are at distance r from the left side of the square,

and at least two points are at distance r from the right

side of the square.

Proof. The ﬁrst thing to notice is that Theorem 3.1

refers to PPS. To adapt it for PECS, we have to re-

call that when a point belongs to an edge in PPS, this

means that the point is at distance r from that edge in

PECS.

Consider the left side of the square, and call v

the bottom-left vertex, while v

is the top-left one; by

Theorem 3.1, we can have four different situations:

1. we have a point in v

and one in v

;

2. we have a point in v

, and we have 2 other points:

one on the left side of the square, one on the top

side;

3. we have a point in v

, and we have 2 other points:

one on the left side of the square, one on the bot-

tom side;

4. we have one point on the left side of the square

and one on the top side; furthermore, we have an-

other point on the left side and one on the bottom

side.

In all these cases, we have at least two points on

the left side of the square. A similar idea can be used

to prove the same for the right side of the square.

For PECS, as explained earlier, this means that at

least 2 points are at distance r from the left side, and

at least 2 points are at distance r from the right side.

Moreover, it is true even if we consider the other pair

of opposite edges (that is top/bottom) in place of the

left/right one.

The previous theorem allows us to ﬁx 2 points at

distance r to the left side of the square, and other 2

points at distance r from the right side of the square.

Since we want to respect also the order inequalities

(9), we can express Theorem 3.2 by means of these

new constraints:

∀i ∈ {1, 2} x

= r (10)

∀i ∈ {n − 1, n} x

= 1 − r. (11)

3.2 Bounds Constraints

As remarked in (Anstreicher, 2009), the following

statements hold wlog:

• at least n

= d

e points are on the left half of the

square (we call it x bounds constraints);

• among the previous n

points, at least n

= d

are on the bottom half (y bounds constraints).

Unluckily, this is not true if we have also the order

constraints (9): for example, the optimal solution of

PECS when n = 8 does not respect all these con-

straints together. In fact, as can be seen in Figure 1, if

the solution respects both the order constraints and the

x bounds constraints we cannot have the circles 1 and

2 in the bottom half of the square (that is y

≤ 0.5 and

≤ 0.5, since n

= 2), so the y bounds constraints do

not hold.

We can conclude that the x bounds constraints can

be adjoined to the PECS model with order constraints,

but not with the y bounds constraints. Actually, as

claimed in (Anstreicher, 2009), it is possible to have

together the order constraints (9), the x bounds con-

straints and the y bounds constraints if we drop the

order constraint x

≤ x

. However, we need to

preserve the order constraints to derive the “triangu-

lar inequality constraints” presented in Section 3.3.

SYMMETRY BREAKING CONSTRAINTS FOR THE PROBLEM OF PACKING EQUAL CIRCLES IN A SQUARE

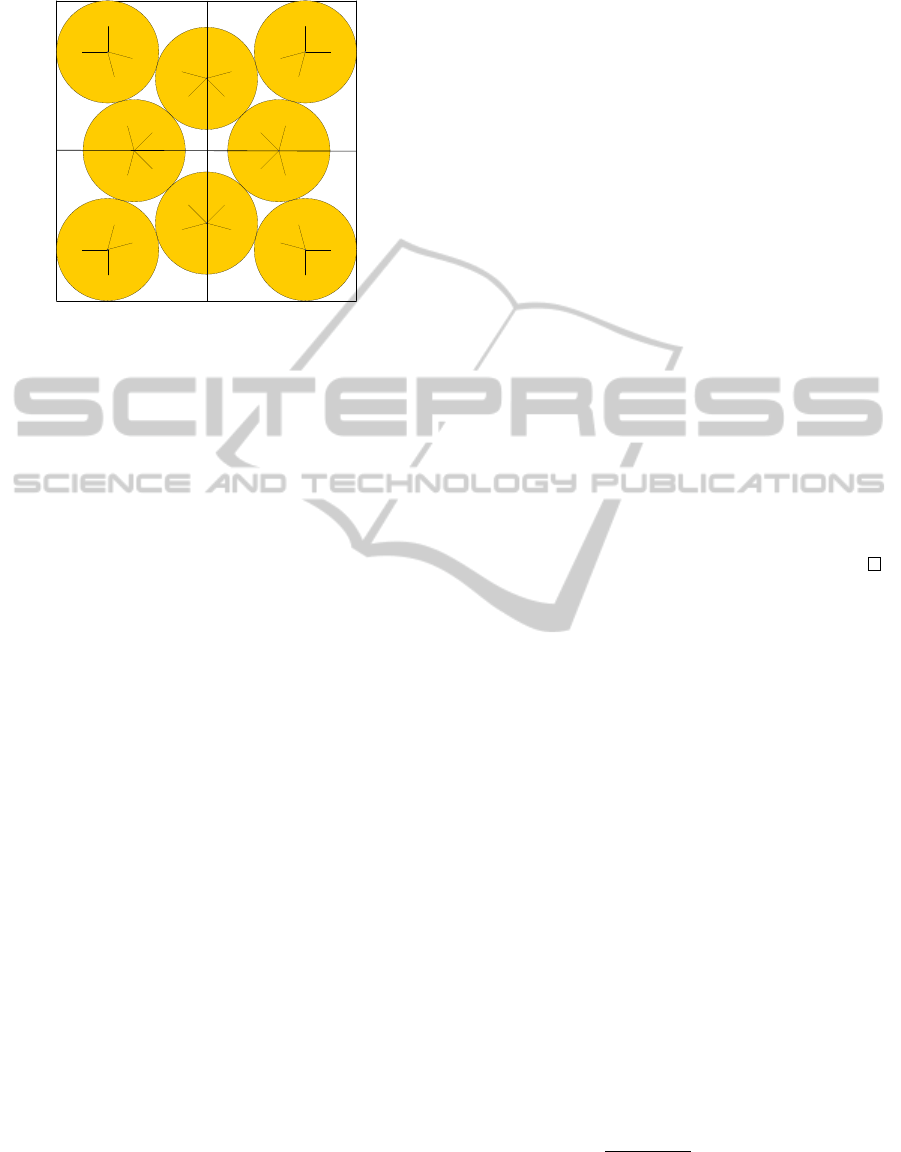
8 circles in a square

radius = 0.170540688701

ratio = 5.863703305156

density = 0.730963825254

contacts = 20



E.SPECHT

01-SEP-2009

Figure 1: Optimal solution of PECS for n = 8 (this ﬁgure is

taken from http://www.packomania.com).

Hence, we will show how to formulate in another

way the y bounds constraints, in order to add them to

the model, and how to add the x bounds constraints

using a single inequality.

The latter can be done this way: since the order

constraints hold, it is sufﬁcient to add the following

inequality:

≤ 0.5. (12)

Thus, the inequalities x

≤ 0.5, ∀i ≤ n

are automati-

cally satisﬁed.

The former problem is basically the following:

among the n

points that are on the left half of the

square, at least n

are on the bottom half, but we can-

not know which points are on the bottom half; never-

theless, we can obtain an inequality on the sum of the

y components of the ﬁrst n

points.

More precisely, n

points have the coordinates y

which are less or equal to 0.5. For the others n

− n

the y coordinates are less or equal to 1 − r. Hence, we

can write the following inequality:

∑

i=1

≤ (n

) · 0.5 + (n

− n

) · (1 − r). (13)

Using the same idea, we can obtain something

similar for the sum of the x components of all the

points.

Basically, n

points have the coordinates x that are

less or equal to 0.5; among them, two have coordi-

nates ﬁxed to r, as shown by (10). For the others

n − n

the x coordinates are less or equal to 1 − r. So,

we can write this inequality:

∑

i=1

≤ (n

− 2) · 0.5 + 2r + (n − n

) · (1 − r). (14)

3.3 Triangular Inequality Constraints

From the triangular inequality, we can write

− x

| + |y

− y

| ≥ d

i j

≥ 2r, ∀i < j ≤ n, (15)

where d

i j

represents the distance between the centers

of the circles i and j.

The order constraints (9) imply that x

− x

≥

0, ∀i < j ≤ n. Hence, we can remove the absolute

value on the x variables from (15) obtaining

− x

+ |y

− y

| ≥ 2r, ∀i < j ≤ n. (16)

Our aim is to remove the absolute value from the

y variables, since it is a source of non-linearity and

makes the inequality not easy to solve. In order to

get the ﬁnal set of constraints, we should prove the

following proposition:

Proposition 3.1. Given the constraints (3)-(9) of the

PECS, the following inequalities hold:

+ y

≥ |y

− y

| + 2r, ∀i < j ≤ n. (17)

Proof. We can suppose wlog that y

≥ y

. Hence y

≥ y

− y

+ 2r, ∀i < j ≤ n. This is equivalent to

≥ r, ∀i < j ≤ n, that is obviously true, since these

inequalities are equivalent to (7).

At this point, we can remove the absolute value on

the y variables by replacing |y

− y

| with y

+ y

−x

−2r ≥ x

−x

+|y

−y

| ≥ 2r, ∀i < j ≤ n.

(18)

Finally we obtain the constraints:

− x

+ y

≥ 4r, ∀i < j ≤ n. (19)

4 NUMERICAL RESULTS

In this section we compare two formulations of PECS

for the instances where 4 ≤ n ≤ 20: the original for-

mulation with the order constraints (2)-(9) (PECS +

ordering), and the same formulation with all the new

constraints proposed in Section 3, i.e., (10)-(14),(19)

(PECS + all). Our comparative results, shown in

Table 1, have been obtained on a 2.4 GHz Intel

Xeon CPU with 24 GB RAM running Linux and

the solver COUENNE (Belotti et al., 2009); the ta-

ble displays the following statistics for the two for-

mulations: objective function value f

∗

of the incum-

bent, gap still open (we use the CPLEX deﬁnition

(ILOG, 2009):



100·| f

∗

− f

| f ∗+10

−10



%, where f

is the

best upper bound found in the case of maximization

problems), number of BB nodes closed, number of

BB nodes still on the tree and the second of CPU

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

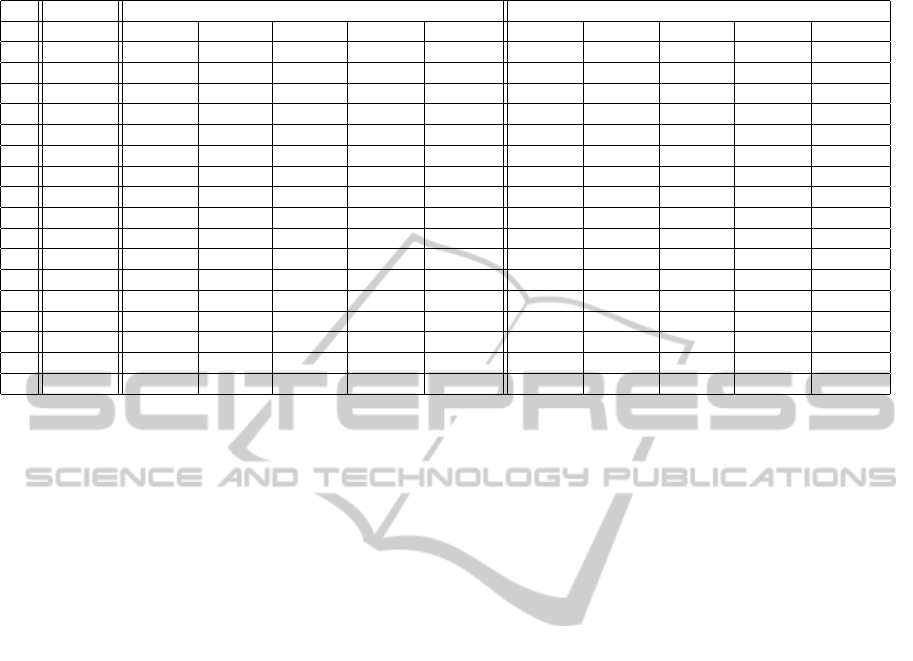
Table 1: Results obtained by running COUENNE on some PECS instances.

PECS + ordering PECS + all

n r

∗

f ∗ gap n. closed n. on tree CPU time f ∗ gap n. closed n. on tree CPU time

4 0.25 0.25 0% 0 0 0.12 0.25 0% 0 0 0.13

5 0.207107 0.207107 0% 2 0 0.44 0.207107 0% 2 0 0.19

6 0.187681 0.187703 0% 8456 0 17.90 0.187713 0% 110 0 7.25

7 0.174458 0.174458 0% 245102 0 728.69 0.174458 0% 564 0 17.11

8 0.170541 0.170541 17.71% 1853359 117869 7200 0.170541 0% 7822 0 65.78

9 0.166667 0.166667 30.55% 1365445 279773 7200 0.166667 0% 66070 0 525.75

10 0.148204 0.148201 65.10% 1230472 334114 7200 0.148204 32.22% 611560 201488 7200

11 0.142399 0.142399 75.62% 1068775 290037 7200 0.142339 39.61% 498050 179367 7200

12 0.139959 0.139959 78.64% 899535 273315 7200 0.139959 59% 365384 136656 7200

13 0.133994 0.133993 110.67% 816573 232735 7200 0.133993 53.57% 337112 133403 7200

14 0.129332 0.129332 119.10% 615348 182939 7200 0.129332 74.04% 250406 97740 7200

15 0.127167 0.126478 124.75% 853025 245904 7200 0.127167 77.19% 204853 81901 7200

16 0.125 0.125 100.38% 382247 121598 7200 0.125 77.40% 173767 70580 7200

17 0.117197 0.116293 115.19% 275094 98707 7200 0.117111 91.16% 148004 61668 7200

18 0.115521 0.113218 175.46% 433224 140861 7200 0.115521 101.74% 129641 53367 7200

19 0.112265 0.11174 179.20% 454058 158505 7200 0.111911 104.83% 111486 44392 7200

20 0.111382 0.111382 210.63% 342260 116599 7200 0.111382 108.65% 90274 35542 7200

time taken (with a time limit of 2h). Moreover, we

show also the optimal solutions r

∗

for the instances,

which can be found on (Szab

o et al., 2007) or in

http://www.packomania.com.

5 CONCLUSIONS

The new constraints proposed in this paper increase

signiﬁcantly the performance of COUENNE with re-

spect to the formulation (2)-(9), as shown in Table 1.

As a matter of fact, the time to obtain the optimal so-

lution is lower, and when the time limit is reached for

both formulations, the gap is smaller. This means that

the formulation “PECS + all” leads to a lower value

of the Upper Bound for r.

Looking at the number of nodes, we can see that

the trees associated to the “PECS + all” formulation

are smaller than the trees obtained with “PECS + or-

der”, as expected.

Furthermore, in four cases the incumbent found

with the “PECS + all” formulation is better than the

one found with the “PECS + ordering” formulation

(in two cases, n = 15 and n = 18, the value is equal to

the optimum).

Hence, even if we test these formulations on a

small number of instances, it is quite evident that

“PECS + all” outperforms “PECS + ordering”.

Looking at the n = 6 case in the table, we see that

the incumbent values found are higher than the op-

tima, but this is due to the numerical approximation

of COUENNE.

It is also interesting to notice that the constraint

(14) might seem redundant if we have the constraints

(4), (6), (9), (10) and (12). Actually, some tests

show that this inequality helps to obtain better Up-

per Bounds, above all with big instances of PECS.

The reason for this behaviour could be that COUENNE

uses this constraint to derive some cuts, which are au-

tomatically adjoined to the mathematical model.

The future work has two main directions: ﬁrst, we

want to investigate more the PECS problem, in order

to ﬁnd new SBCs. For instance, another class of SBCs

proposed in (Costa et al., 2010b), which mix inequal-

ities on the x and on the y variables, leads to better

results with respect to the order constraints. We can

try to use these constraints in our model, but some ad-

justments are required, since the new constraints pro-

posed in this paper depend on the hypothesis that the

order inequalities are satisﬁed.

Second, we want to perform some experiments

with bigger instances and bigger time limits, in order

to ﬁnd the maximal size of PECS that it is possible to

solve with this mathematical programming approach.

ACKNOWLEDGEMENTS

Financial support by grants: Digiteo 2009-14D “RM-

NCCO”, Digiteo 2009-55D “ARM” is gratefully ac-

knowledged.

REFERENCES

Anstreicher, K. (2009). Semideﬁnite programming versus

the reformulation-linearization technique for noncon-

vex quadratically constrained quadratic programming.

Journal of Global Optimization, 43:471–484.

Belotti, P., Lee, J., Liberti, L., Margot, F., and W

achter, A.

(2009). Branching and bounds tightening techniques

SYMMETRY BREAKING CONSTRAINTS FOR THE PROBLEM OF PACKING EQUAL CIRCLES IN A SQUARE

for non-convex MINLP. Optimization Methods and

Software, 24(4):597–634.

Boll, D. W., Donovan, J., Graham, R. L., and Lubachevsky,

B. D. (2000). Improving dense packings of equal disks

in a square. The Electronic Journal of Combinatorics,

Casado, L. G., Garcia, I., Szab

o, P. G., and Csendes, T.

(2001). Packing equal circles in a square ii. - new re-

sults for up to 100 circles using the tamsass-pecs algo-

rithm. In Optimization Theory: Recent Developments

from M

atrah

aza, pages 207–224.

Costa, A., Hansen, P., and Liberti, L. (2010a). Formula-

tion symmetries in circle packing. In Mahjoub, R.,

editor, Proceedings of the International Symposium

on Combinatorial Optimization, volume 36 of Elec-

tronic Notes in Discrete Mathematics, pages 1303–

1310, Amsterdam. Elsevier.

Costa, A., Hansen, P., and Liberti, L. (2010b). Static sym-

metry breaking in circle packing. In Faigle, U., editor,

Proceedings of the 9

Cologne-Twente Workshop on

Graphs and Combinatorial Optimization, pages 47–

50. University of K

oln.

Graham, R. L. and Lubachevsky, B. D. (1996). Repeated

patterns of dense packings of equal disks in a square.

The Electronic Journal of Combinatorics, 3(1).

ILOG (2009). ILOG CPLEX 12.1 User’s Manual. ILOG

S.A., Gentilly, France.

Liberti, L. (2006). Writing global optimization software. In

Liberti, L. and Maculan, N., editors, Global Optimiza-

tion: from Theory to Implementation, pages 211–262.

Springer, Berlin.

Liberti, L. (2008). Automatic generation of symmetry-

breaking constraints. In Yang, B., Du, D.-Z., and

Wang, C., editors, COCOA Proceedings, volume 5165

of LNCS, pages 328–338, Berlin. Springer.

Liberti, L. (2009). Reformulations in mathematical pro-

gramming: Deﬁnitions and systematics. RAIRO-RO,

43(1):55–86.

Liberti, L. (2010). Reformulations in mathematical pro-

gramming: automatic symmetry detection and ex-

ploitation. Mathematical Programming, pages 1–32.

Locatelli, M. and Raber, U. (1999). Packing equal circles

in a square: I. theoretical results. Technical Report

08-99, Dip. Sistemi e Informatica, Univ. di Firenze.

Locatelli, M. and Raber, U. (2002). Packing equal circles

in a square: a deterministic global optimization ap-

proach. Discrete Applied Mathematics, 122(1-3):139–

166.

Nurmela, K. J. and

Osterg

ard, P. R. J. (1997). Packing up

to 50 equal circles in a square. Discrete & Computa-

tional Geometry, 18(1):111–120.

Raber, U. (1999). Nonconvex all-quadratic global optimiza-

tion problems: solution methods, application and re-

lated topics. PhD thesis, University of Trier, Germany.

Sahinidis, N. and Tawarmalani, M. (2005). BARON 7.2.5:

Global Optimization of Mixed-Integer Nonlinear Pro-

grams, User’s Manual.

Smith, E. and Pantelides, C. (1999). A symbolic refor-

mulation/spatial branch-and-bound algorithm for the

global optimization of nonconvex MINLPs. Comput-

ers & Chemical Engineering, 23:457–478.

Szab

o, P. G. (2005). Optimal substructures in optimal and

approximate circle packings. Beitrage zur Algebra

und Geometrie (Contributions to Algebra and Geom-

etry), 46:103–118.

Szab

o, P. G., Mark

ot, M. C., Csendes, T., Specht, E.,

Casado, L. G., and Garca, I. (2007). New Ap-

proaches to Circle Packing in a Square: With Program

Codes (Springer Optimization and Its Applications).

Springer-Verlag New York, Inc., Secaucus, NJ, USA.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems