HYBRID COLUMN GENERATION-BASED APPROACH FOR VRP

WITH SIMULTANEOUS DISTRIBUTION, COLLECTION,

PICKUP-AND-DELIVERY AND REAL-WORLD SIDE

CONSTRAINTS

Lorenzo Ruinelli, Matteo Salani and Luca Maria Gambardella

IDSIA/USI-SUPSI, Dalle Molle Institute for Artiﬁcial Intelligence, Galleria 2, 6928 Manno, Switzerland

Keywords:

Vehicle routing, Hybrid optimization, Column generation.

Abstract:

We present an optimization algorithm that hybridizes heuristic and exact methods to solve the problem of a

real-world distribution company. Our algorithm combines three existing optimization techniques (Ant Colony

Optimization, Column Generation and Mixed Integer Programming). Standard Column Generation is im-

proved with an incremental search technique able to speed up the entire process. We present computational

results on 14 real-world instances obtained from our industrial partner. Finally, we compare the solutions ob-

tained by our algorithm against those currently computed by the route planning ofﬁce of our industrial partner.

Beside cost savings, we asses the reliability of our approach in terms of computational time and quality.

1 INTRODUCTION

The Vehicle Routing Problem (VRP) is a hard combi-

natorial optimization problem. VRP is widely studied

in Operation Research as its application in real-world

logistic companies is highly relevant (Golden et al.,

2008; Ceselli et al., 2009). Optimal route planning

allows for substantial savings in transportation costs

(Toth and Vigo, 2002).

The methods for the solution of hard combinato-

rial optimization problems can be exact or heuristic.

Many exact methods use an enumeration tree to pro-

duce a guaranteed optimal solution (Wolsey, 1998).

These methods are based on efﬁcient computation of

valid primal and dual bounds. On the other hand,

heuristic methods do not guarantee optimal solution

but can be much faster than exact ones. Exact and

heuristic approaches can be hybridized in order to

increase the efﬁciency and ﬂexibility of the solution

process (Doerner and Schmid, 2010).

In this paper, we address a routing problem aris-

ing from a collaboration with a real-world distribu-

tion logistic company. The problem consists in com-

puting the daily plan of a heterogeneous ﬂeet of ve-

hicles. Our approach combines three optimization

techniques: an Ant Colony Optimization System, a

Column Generation algorithm and a general purpose

Mixed Integer Programming (MIP) solver. The pro-

posed algorithm can be used to compute tight lower

bounds of complex instances. Moreover, exploit-

ing the notion of exact and heuristic hybridization

methods, we impose a time-limit on each component

within the algorithm, and we devise an incremental

search space that improves the standard column gen-

eration procedure. We prove the effectiveness of the

algorithm providing good feasible solutions for 14

real-world instances in a reasonable amount of time.

Finally, we discuss the possible impacts of the intro-

duction of our optimization framework into the exist-

ing infrastructure of our industrial partner.

The incremental search space column generation

and its application to a real-world routing problem are

original contributions of this paper.

In section §2 we provide relevant pointers to liter-

ature describing features that relate with our problem.

In §3 we brieﬂy describe the routing problem, in §4

and §5 we outline the model and the solution algo-

rithm, respectively. Finally, in sections §6 and §7 we

provide computational experiments and consider in-

dustrial aspects arising from the use of our software

by our industrial partner. Section §8 concludes the

paper.

247

Ruinelli L., Salani M. and Maria Gambardella L..

HYBRID COLUMN GENERATION-BASED APPROACH FOR VRP WITH SIMULTANEOUS DISTRIBUTION, COLLECTION, PICKUP-AND-DELIVERY

AND REAL-WORLD SIDE CONSTRAINTS.

DOI: 10.5220/0003713702470255

In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 247-255

ISBN: 978-989-8425-97-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 LITERAURE REVIEW

Recent contributions to the exact solution of realistic

versions of the VRP are mainly based on branch-and-

price-and-cut. In its basic version, the VRP is solv-

able to optimality for instances with up to 200 cus-

tomers (Baldacci et al., 2008). Problems with time

windows are considered in (Desaulniers, 2010). In

(Archetti et al., 2006; Sharda et al., 2008; Nowak

et al., 2009; Desaulniers, 2010), authors present ad-

vances in real-world feature modeling. As we also

do in this paper, they consider splittable loads in

which each customer can be served by more than

one vehicle. More recently, in (Salani and Vacca,

2011), authors address a VRP with discrete split,

load-dependent service time and time windows using

a branch-and-price algorithm based on column gener-

ation and present computational results on instances

based on Solomon’s data set. Whereas, in (Ceselli

et al., 2009), authors propose a branch-and-price al-

gorithm to solve a real-world VRP with similar fea-

tures of that addressed in this paper and present com-

putational results on real instances obtained from a

provider of software-planning tools for distribution

logistics companies.

In (Rizzoli et al., 2007), authors discuss the appli-

cation of heuristic methods based on Ant Colony Op-

timization to a number of real-world problems (VRP

with time windows, VRP with collection and delivery,

time dependent VRP where the travel times depend on

the time of the day and on-line VRP where customers’

orders arrive during the delivery process).

The hybridization of exact and heuristic meth-

ods to solve VRP has emerged in several paper. In

(Archetti et al., 2008), a Split Delivery Vehicle Rout-

ing Problem is modeled as a Set Covering Problem

and solved iteratively using a tabu search algorithm to

identify promising set of routes and an Interger Lin-

ear Program (ILP) to select the best routes. The al-

gorithm has been tested on instances up to 200 nodes

with an execution time up to one hour. In (Schmid

et al., 2009) a Ready-Mixed Concrete Delivery prob-

lem is solved providing excellent quality results in

medium-sized real-world test instances. The prob-

lem has been formulated as an integer multicommod-

ity ﬂow (MCNF) and solved by an algorithm that it-

eratively uses a variable neighborhood search com-

ponent (VNS) to generate fulﬁllment patterns; the

MCNF selects the best fulﬁllment patterns. (Salari

et al., 2010) proposes a heuristic improvement proce-

dure to solve an Open VRP (a VRP where the vehicles

are not required to return to the depot). The problem

has been formulated as a reallocation model (an ILP)

and solved applying a destruct-and-repair paradigm:

a heuristic procedure (HP) randomly destroy the cur-

rent solution (using dual information of the ILP re-

stricted relaxation); the destroyed solution is then re-

paired by solving the ILP model in the attempt of ﬁnd-

ing a new improved solution. The provided experi-

mental results, based on benchmark instances up to

400 nodes, show that the algorithm is able to improve

the solution found by the most effective metaheuristic

techniques.

3 THE PLANNING PROBLEM

Our algorithm solves the planning problem of a real-

world distribution company that has to compute the

daily distribution plan of his ﬂeet of vehicles.

Customers demand for the delivery, the collection

or the pickup-and-delivery of discrete items is orga-

nized in orders. Demand is known in advance.

The ﬂeet of vehicles is composed of heteroge-

neous vehicles that refer to one depot. Routes do

not necessarily start or end at the depot. Each vehi-

cle presents a set of characteristics.

The problem presents the following characteris-

tics:

• multi-dimension capacities (volume, weight,

value, etc...), route limits (length and duration)

and workforce rules (driving times and working

shifts);

• multiple time windows (e.g., morning and after-

noon) associated with depot, customer and vehi-

cles;

• the option of splitting up the orders;

• the option of “open” routes that do not terminate

at depot and/or do not depart from the depot.

• load-dependent service time;

• compatibility constraints between vehicles and lo-

cations. Compatibilities between customers and

vehicles are expressed as the set of required vehi-

cle’s characteristics.

• customers can be skipped, which involves a mon-

etary penalty.

• involving system of fares (similar to that of (Ce-

selli et al., 2009)) with the additional feature of

fare-dependent feasibility constraints;

Customers are organized in hierarchical clusters,

called primary and secondary zones, mainly related

to regional districts and provinces. Each cluster is

associated with a set of fares and capacity limits.

When a vehicle traverses a cluster it is subject to

fares and capacity limits for the entire duration of

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

248

the tour. In practice, the prolem presents “route de-

pendent” constraints. As a consequence, some of the

recently developed advances (e.g. the bi-directional

dynamic programming approaches of (Righini and

Salani, 2006)) cannot be used.

Our problem consists of ﬁnding an optimal daily

plan which minimizes the routing costs and the

penalty costs of skipping customers.

Case Study. The distribution company operates in

the ﬁeld of logistics under controlled temperature and

its customers are distributed in Italy. Our relations

with the distribution company are mediated by An-

tOptima that is a provider of software planning tools.

The characteristics of the considered distribution lo-

gistic company are as follows:

• Operates in Italy.

• Heterogeneous ﬂeet of 140 vehicles.

• Up to 200 customers/day.

• Average operating costs of 30’000 e/day.

4 PROBLEM MODELLING

The optimal solution of our VRP consists on a daily

plan serving all customers with minimal cost. Serving

a customer means to deliver, to collect or to pickup-

and-deliver its goods. The goods of a customer can be

aggregated becoming an item. A daily plan is made

of tours. A tour has a cost, is achievable by a vehicle

type and serves items. Each vehicle can do at most

one tour.

This problem can be mapped to a Set Partitioning

Problem where tours are sets and elements to be cov-

ered are items. The mathematical formulation of our

problem is the following:

minimize

∑

p∈P

∑

k∈Ω

∑

q∈Q

(1)

∑

p∈P

∑

k∈Ω

+ y

= 1 ∀q ∈ Q (2)

∑

k∈Ω

<= n

∀p ∈ P (3)

∈ {0, 1} ∀p ∈ P, ∀k ∈ Ω

. (4)

In this model, commonly referred as Master Prob-

lem (MP), P is the set of vehicle types and n

rep-

resents the maximum number of vehicles of type p

available per day. Q is the set of items to be deliv-

ered. Ω

is the set of tours that can be assigned to a

vehicle of type p ∈ P in one day. Each coefﬁcient x

1 if item q is delivered along tour k ∈ Ω

, 0 otherwise.

For each tour k ∈ Ω

, the variable z

takes value 1 if

tour is selected, 0 otherwise. For each item q ∈ Q, y

takes values 1 if the item is not delivered, 0 otherwise.

Partitioning constraints (2) impose that each item is

served. These constraints can be rewritten as cover-

ing constraints (≥) when triangular inequality holds

for the cost structure which is not the case of our ap-

plication. Constraints (3) limit the number of tours

assigned to vehicles of the same type.

The objective function (1) minimizes the total

traveling costs plus the loss of revenue induced by a

non delivered item d

The master problem model may contain a num-

ber of variables, which grows exponentially with the

size of the instance. To compute a valid lower bound,

we recour to column generation. In particular, we re-

lax integrality conditions on binary variables and con-

sider a Restricted Master Problem (RMP). Initially,

the set of tour is empty but feasible solution is ensured

by y variables. The cost d of the exclusions should

be big enough to push the algorithm to ﬁnd proﬁtable

tours which are dinamically generated solving pricing

subproblems, one for each vehicle type P.

The Pricing Problem. At each column generation

iteration the linear relaxation of the RMP is solved,

and we search for new columns with negative reduced

cost. The reduced cost of each column k ∈ Ω

is:

= c

−

∑

q∈Q

− γ

(5)

where π

is the nonegative dual variable associ-

ated to the qth constraint of the set (2) and γ

is the

nonpositive dual variable associated with the pth con-

straint of the set (3).

Hence, instead of explicitly computing the re-

duced cost of all the variables in the problem, we

solve a pricing problem, one for each vehicle type

p ∈ P. If columns with negative reduced cost are

found, they are inserted into the RMP and the process

is iterated; otherwise, the optimal solution of the lin-

ear relaxation of the RMP is also an optimal solution

of the linear relaxation of the MP.

5 A COLUMN GENERATION

HEURISTIC

In this section, we present an algorithm that combines

three optimization techniques to produce heuristically

VRP solutions with a measures of their quality.

HYBRID COLUMN GENERATION-BASED APPROACH FOR VRP WITH SIMULTANEOUS DISTRIBUTION,

COLLECTION, PICKUP-AND-DELIVERY AND REAL-WORLD SIDE CONSTRAINTS

249

Components. Our algorithm is made of three com-

ponents: an Ant Colony Optimization system (ANT),

a Column Generation algorithm (CG) and a general

purpose MIP solver (S). Figure 1 reports the compo-

nents and their interactions. Each component is rep-

resented by a box whereas input and output of each

component is reported on the links between compo-

nents.

ANT is an implementation of the Ant Colony Op-

timization System presented in (Gambardella et al.,

1999). It has been provided by AntOptima, which

also adapted it to the problem of our industrial partner.

ANT produces rapidly (in about 10 minutes) heuristic

initial solutions.

CG is a column generation algorithm that is ﬁrst

initialized with the solution provided by ANT and

then optimally solved. Its objective value is a lower

bound (LB) of our problem and the columns of its MP

are used to form a MIP.

Finally, the MIP is solved by a general purpose

commercial solver S (the MIP always admits an inte-

ger feasible solution as the MP is initialized with the

solution produced by ANT). The solution of the MIP

is a plan and its quality can be measured using the LB

computed by CG.

Components ANT and S are used as black-boxes,

while CG has been designed and implemented by us.

For this reason we provide a more in depth description

of this component.

Figure 1: Algorithm components and interactions.

Column Generation (CG). The initialization of

CG is done using a feasible solution previously com-

puted by ANT. This solution is a set of tours, which

is used as initialization columns of the RMP, and rep-

resents an upper bound (UB) of our optimization pro-

cess. The Column Generation procedure is reported

in Algorithm 1.

The column generation algorithm works as fol-

lows: the linear relaxation of the RMP is solved, dual

variables are collected and then multiple-pricing al-

gorithms are solved to ﬁnd columns with negative re-

duced cost. If columns with negative reduced cost are

found, they are inserted into the RMP, and the process

is iterated. Otherwise the iteration ﬁnishes, and the

RMP is optimally solved. We obtain a lower bound

(LB) of our problem, which is the objective function

value of the linear relaxation of the RMP, and we can

create the corresponding MIP. The MIP is an RMP

with the integrality constraints on the tours selection:

the MIP is solvable by a generic commercial solver.

Algorithm 1: Column Generation.

input InitialSolution

RMP ← InitialSolution

repeat

LB = solve (1) − (3)

for k ∈ K do

¯c

= solve (5) (pricing for vehicle k)

end

until min

k∈K

¯c

< 0 ;

output MIP, LB

The pricing problem can be modeled as a resource

constrained elementary shortest path problem (RCE-

SPP). The RCESPP is the problem of ﬁnding the min-

imum cost elementary path and, since the underlying

graph may have negative cost cycles, is strongly NP-

hard (Dror, 1994).

The underlying graph G(V, A) is made of a set V

of vertices and a set of A arcs. Let N be the set of

items. Then V = N ∪ {s,t}, where s and t are special

vertices representing the depot. A non-negative prize

is associated with each vertex i ∈ N representing a

delivery point, a collection point or the delivery point

of a pick-up and delivery pair. A vehicle must go from

s to t, visiting a subset of the other vertices; no cycles

are allowed. The objective is to minimize the cost,

given by the sum of the costs of the arcs traversed

minus the sum of the prizes collected at the vertices

visited. Arc costs are computed according to a system

of fares that depends on the visited locations.

The basic dynamic programming approach to

the RCESPP is based on the algorithm devised by

(Desrosiers et al., 1981) for the RCSPP (an extension

of the Bellman-Ford algorithm with the addition of

resource constraints).

The algorithm assigns states to each vertex: each

state of vertex i represents a path from s to i . Each

state has an associated resource consumption vector R

and each component of R represents the consumption

of a different resource along the path. R encodes the

set of visited items as a binary vector which ensures

path’s elementarity. Each state has an associated cost

C and the optimal solution is given by the minimum

cost state associated with t.

Constraints on the consumption of resources can

be route dependent. For this reason not all state-of-

the-art techniques can be used (e.g., bi-directional dy-

namic programming, (Righini and Salani, 2006)).

The previous pricing algorithm has an exponen-

tial worst case time complexity. For this reason we

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

250

devised three pricing algorithms of increasing com-

plexity: a greedy pricing (GP), a heuristic pricing

(DPH) and an exact pricing (DPE). DPE solves the

pricing problem to optimality, while G and DPH look

heuristically for good solutions. The advantage of GP

and DPH compared to DPE is the necessary compu-

tational time to converge. A multi-pricing approach

allow to deal more efﬁciently with the complexity of

the problem, in fact we use GP and DPH to rapidly

ﬁnd columns for each vehicle type P, while DPE is

executed only to prove the optimality of the RMP.

The dynamic programming algorithm is used heuris-

tically considering a subset of resources within the

dominance test (number of item served and time con-

sumption). GP is a constructive greedy algorithm that

builds the tours visiting the most proﬁtable items ﬁrst

until some resource constraint is violated.

Incremental Search (CG-IS). In order to further

speed up the computation time, we devised an incre-

mental search that extends the standard column gener-

ation procedure (CG-STD) presented in the previous

paragraph.

The basic idea is the following: we start generat-

ing columns for a subnetwork using the heuristic pric-

ing algorithms (DPH and GP). When heuristic pricing

algorithms stop ﬁnding columns on the subnetwork,

we increase its dimension and we start again the col-

umn generation algorithm. We repeat this procedure

until the subnetwork is equal to the original one. At

this point we execute also the exact pricing (DPE) to

prove the optimality of the solution.

Algorithm 2: Incremental Column Generation.

input InitialSolution, R ≤ 1

RMP ← InitialSolution

repeat

R = R + ∆R

= NetworkReduction(R)

repeat

LB = solve (1) − (3)

for k ∈ K do

¯c

= solve (5) on G

using GP

if ¯c

≥ 0 then

¯c

= solve (5) on G

using DPH

end

if ¯c

≥ 0 and R == 1 then

¯c

= solve (5) on G

using DPE

end

until min

k∈K

¯c

< 0 ;

until R < 1 ;

output MIP, LB

Network Reduction. The subnetwork is obtained

through a heuristic procedure outlined in Algorithm 3.

The procedure reduces the dimension of the problem

removing arcs from the underlying network. The re-

sult is a subnetwork of the problem. Let G

= (V

, A

)

be the reduced graph representing the subset of the

problem and R (0 > R ≤ 1 ) is the desired size of the

subset. Let δ

−

(S ∈ V ) be the set of arcs with the tail

in the set S. The idea is to remove arcs from A

until

their number |A

| is less or equal the desired number

of arcs.

Let v

max

be the vertex with the highest number of

outgoing arcs within V

and a

max

be the longest arc

within outgoing arcs of v

max

: a

max

is removed from

and the process iterates.

Algorithm 3: Network Reduction.

input R < 1

= G

while |A

| > R × |A| do

max

= arg max

v∈V

|δ

−

({v})|

max

= arg max

a∈δ

−

({v

max

})

length(a)

= A

\ {a

max

}

end

output G

6 COMPUTATIONAL RESULTS

For our experiments we used real world data provided

by the industrial partner. We considered 14 instances

that are 14 plans, each plan is a set of items (de-

liveries, collections and pickup-and-deliveries) for a

speciﬁc day. Detailed information concerning those

datasets are reported in Table 1. The ﬁrst column of

the table reports the name of the instance, which con-

sists on the date of the plan, the second column reports

the corresponding day of the week, then the number

of vehicle types, the next column represents the arcs

in the transportation network. The last 4 columns re-

port the number of items and their repartition between

delivery, collection and pickup-and-delivery. The av-

erage number of items within an instance is 160, the

biggest instance is the 08.03.2010 and contains 201

items, the smallest instance is the 07.10.2010 and con-

tains 115 items.

Our algorithm allows to obtain solutions with a

measure of their quality. The payload of the method

is the time required to provide that measure. Unfor-

tunately real-world logistic companies operate with

tight deadlines, the instances are big and the algo-

rithm execution time becomes then a key-factor for

its application. Dimension of real-world instances

and time constraint imposed by our industrial part-

HYBRID COLUMN GENERATION-BASED APPROACH FOR VRP WITH SIMULTANEOUS DISTRIBUTION,

COLLECTION, PICKUP-AND-DELIVERY AND REAL-WORLD SIDE CONSTRAINTS

251

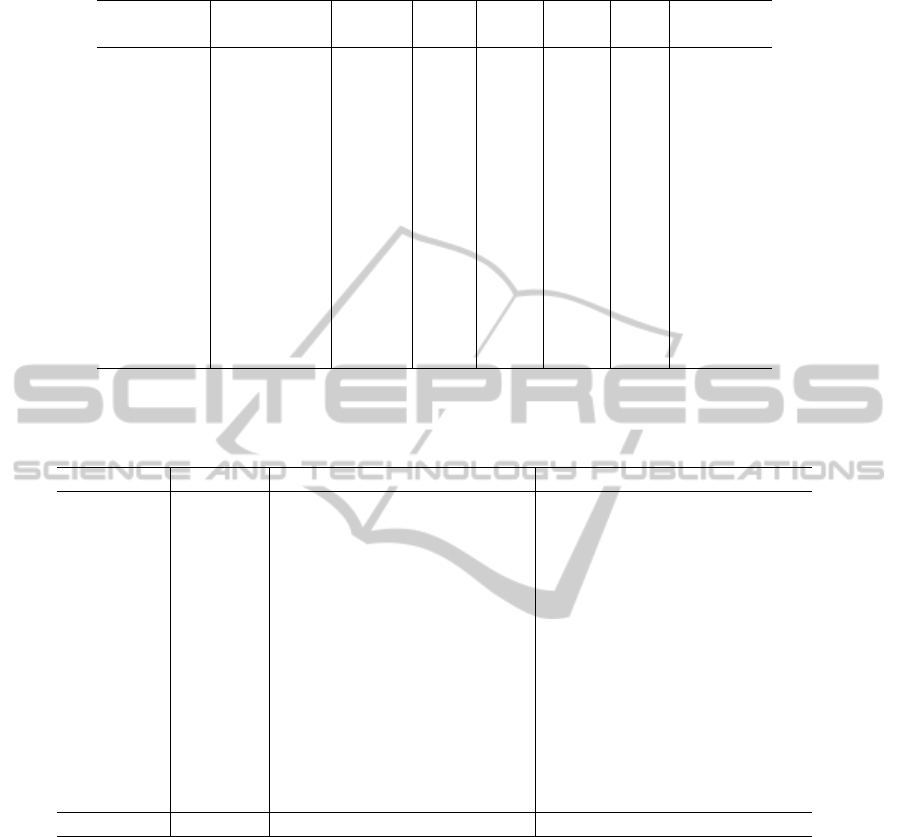
Table 1: Real-world instances.

Instance day of week vehicle arcs items deliv. coll. pickup-

types and-deliv.

08.03.2010 Wednesday 77 4509 201 147 50 4

10.03.2010 Wednesday 75 4611 189 134 52 3

11.03.2010 Thursday 77 4805 191 150 39 2

04.05.2010 Tuesday 74 5513 186 124 57 5

05.05.2010 Wednesday 75 5286 200 148 50 4

14.06.2010 Monday 77 4062 182 132 47 3

06.08.2010 Friday 86 2419 141 96 43 2

20.09.2010 Monday 86 3557 173 129 43 1

21.09.2010 Tuesday 85 2477 138 96 41 1

22.09.2010 Wednesday 87 2388 143 106 36 1

23.09.2010 Thursday 85 2707 142 95 45 2

24.09.2010 Friday 87 2729 148 107 40 1

07.10.2010 Friday 86 1572 115 88 26 1

13.10.2010 Wednesday 89 1480 120 95 24 1

Table 2: Feasible solutions for real-world instances in 30 minutes.

CG-STD CG-IS

Instance LB (e) columns cost (e) gap% columns cost (e) gap%

08.03.2010 40416.81 30002 42330.96 4.74 16740 41840.92 3.52

10.03.2010 - 43603 38734.43 - 18586 37724.37 -

11.03.2010 - 135512 26124.80 - 22475 25724.77* -

05.05.2010 - 67941 40637.43 - 26369 40637.43 -

04.05.2010 - 74115 32534.15 - 26125 30817.00 -

14.06.2010 38628.82 43276 40263.51 4.23 19965 40634.48* 5.19

06.08.2010 19750.82 36568 22388.53 13.35 13867 20673.48 4.67

20.09.2010 36669.24 46741 38078.54 3.84 17827 38258.47* 4.33

21.09.2010 26966.56 28907 30026.83 11.35 13265 28349.77 5.13

22.09.2010 26082.19 31157 27862.82 6.83 11631 27427.74 5.16

23.09.2010 23670.61 32072 24763.71 4.62 11651 24818.63* 4.85

24.09.2010 21031.08 52107 22479.67 6.89 15900 22231.51 5.71

07.10.2010 16850.28 26251 17353.35 2.99 14116 17743.30* 5.30

13.10.2010 21316.61 21837 21939.52 2.92 8058 22140.43 3.86

Averages 47863.50 30394.16 6.18 16898.21 29930.16 4.77

ner led us to limit the execution time of our algo-

rithm. The resulting algorithm is then a heuristic

method and the measure of the quality of the solution

is not guaranteed anymore. In our experimental cam-

paign, we propose a comparison between the algo-

rithm based on the standard column generation proce-

dure (CG-STD) against the algorithm that implements

the devised incremental search (CG-IS). The experi-

ments fulﬁll the time-limit requirement of our indus-

trial partner, which is of 30 minutes. The time alloca-

tion for the components of our algorithm is: ANT ex-

ecuted with a time-limit of 10 minutes, CG executed

with a time-limit of 10 minutes and S executed with

a time-limit of 10 minutes. According to (Ruinelli,

2011), this setting allows to obtain the best perfor-

mances. Results are reported with a gap based on the

lower bound computed using our algorithm without

time-limits.

All tests were performed on a PC equipped with

an Intel Core i7 2.67 GHz 2 Cores processor with 3

GB RAM. The column generation algorithm is coded

in C# 2.0 and the MIP solver is Gurobi 4.0.

The results of ours experiments are reported in

Table 2 that is organized as follows: the ﬁrst col-

umn contains the name of the instance, the second

column reports the lower bound computed for the in-

stance. Columns 3-5 refer to standard column gener-

ation procedure (CG-STD), while columns 6-8 refer

to procedure implementing the devised incremental

search (CG-IS). Column ”columns” reports the num-

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

252

ber of columns of the RMP within component CG at

time-limit. Columns ”cost (e)” and ”gap%” report

the ﬁnal solution provided by our algorithm and its

percentage gap against the lower bound. Entries with

(-) indicates that the algorithm was not able to pro-

duce a lower bound for the instance. Moreover, in

columns 4 and 7, we mark with an asterisk (*) the

solutions of the MIPs that are proven optimal.

From the examination of Table 2, we observe that

our algorithm without time-limit was able to produce

a lower bound for all instances but 4 (for instances

10.03.2010, 11.03.2010, 05.05.2010 and 04.05.2010

the DPE algorithm ran out of memory). Both variants

of our algorithm (CG-STD and CG-IS) always ﬁnd a

feasible solution. CG-STD performs best in 6 over 14

instances while CG-IS does it in 9 over 14 instances.

The solution of instance 05.05.2010 is the same for

both algorithms. We remark that CG-IS performs

best for the 6 more difﬁcult instances (08.03.2010,

10.03.2010, 11.03.2010, 04.05.2010, 05.05.2010 and

14.06.2010). The average cost of the solutions pro-

vided by CG-STD is 30’394.16 e and the average gap

is 6.18%, while the average cost of the solution pro-

vided by CG-IS is 29’930.16 e and the average gap

is 4.77% (the average gap computation does not con-

sider the instances where the lower bound is not avail-

able). CG-STD at time-limit generates always more

columns than CG-IS. The generated columns using

CG-STD is in average 47’863.50, while their aver-

age using CG-IS is 16’898.21. As consequence, the

solver S can solve easier MIPs generated using CG-IS

than those generated using CG-STD. In fact, S proved

the optimality of 5 MIPs, which were all produced by

CG-IS.

Our algorithm allows to deal with real-world in-

stances providing results within 30 minutes of com-

putation and a feasible solution is always ensured by

the initialization provided by ANT.

The devised incremental search (CG-IS) is effec-

tive and improves the CG-STD solutions by 1.52%.

Indeed, the number of columns within the RMP at

time-limit is dramatically reduced (-55%) without af-

fecting their quality. As consequence, the produced

MIP can be solved more easily by the general purpose

solver S.

7 INDUSTRIAL ASPECTS

The efﬁcient deﬁnition of a distribution plan is

a highly relevant activity for logistic companies

(Golden et al., 2008; Ceselli et al., 2009). Our indus-

trial partner currently performs this task manually. Its

route planning ofﬁce, composed by 5 planners, every

morning deﬁne a 24 hours plan to serve the customers

using a given ﬂeet of vehicles. We want to evaluate

the potential impact of the introduction of our opti-

mization algorithm into the existing infrastructure of

our industrial partner. Our evaluation considers the

following aspects (1) time required to plan, (2) distri-

bution cost and (3) quality of the plan. Our analysis is

based on a comparison between two handmade plans

and the solutions provided by our algorithm.

Our industrial partner gave us two hand-

made plans concerning instance 06.08.2010 and

23.08.2010. We don’t have access to the plans of the

other 12 instances. The manual deﬁnition of a plan

requires 5 employees for 4 hours, which are 20 man-

hours. Our algorithm is executed with a time-limit of

30 minutes.

In Table 3 we report the cost comparison between

the handmade plans and the solutions of our algo-

rithm. We observe that our algorithm saves respec-

tively 598 and 590 e. Since our industrial partner

reported that its average operating costs are about

30’000 e/day and the percentage gain achieved by

our algorithm is about 3%, we estimate a potential

saving of 1’050 e/day that are 315’000 e/year (our

partner operates 6 days a week). We remark that al-

gorithm solutions don’t necessarily require the use

of less vehicles than handmade ones. Indeed, for

the instance 06.08.2010 the algorithm solution re-

quires 2 vehicles less than the handmade one (21 in-

stead of 23), while for the instance 23.08.2010 it re-

quires 3 more vehicles (30 instead of 27). Beside cost

minimization, planners implicitly try to minimize the

number of vehicles used. To this extent they decide to

violate some constraints.

Table 3: Costs comparison between handmade plans and

solutions of our algorithm.

Planners Algorithm

20 man/hours 30 min. execution

Instance vehicles cost e vehicles cost e

06.08.2010 23 16723 21 16125

23.08.2010 27 24163 30 23573

To evaluate qualitatively handmade solutions we

validate them using the constraints encoded in our

model. Tables 4 and 5 report the detailed description

of each constraint violation discovered in the hand-

made plans. Table 4 reports the 19 violations related

to instance 06.08.2010, while Table 5 reports the 28

violations releted to instance 23.08.2010. We observe

that most of them represent minor violations but in

the plan related to instance 06.08.2010 we report a

”capacity” violation of 3’686.15 kg, which represents

the 14% of the total capacity of the vehicle, and is thus

HYBRID COLUMN GENERATION-BASED APPROACH FOR VRP WITH SIMULTANEOUS DISTRIBUTION,

COLLECTION, PICKUP-AND-DELIVERY AND REAL-WORLD SIDE CONSTRAINTS

253

Table 4: 19 Violations in the handmade plan of the 06.08.2010.

Time windows 3 violations of 52.38, 63.14 and 310.71 minutes.

Driving time 1 violation of 8.69 minutes.

Working time 2 violations of 20.61 and 1.69 minutes.

System of fares 2 violations.

Compatibility location-vehicle 1 violation.

Max. distances between stops 4 violation of 63.49 , 3.55, 501.52 and 24.32 km.

Capacity 2 violations of 11.28 and 0.16 pallet; 3 violations of 307.4, 631.68 and 3’686.15 kg.

Max. tour lenght 1 violation of 11.37 km.

Table 5: 28 Violations in the handmade plan of the 23.08.2010.

Time windows 3 violations due to visiting closed locations; 2 violations of 141.4 and 66.38 minutes.

Driving time 1 violation of 24.89 minutes.

System of fares 7 violations.

Compatibility location-vehicle 2 violations.

Min. vehicle delivery amount 1 violation of 234 kg.

Max. distances between stops 5 violations of 11.92, 0.84, 8.53, 30.39 and 49.35 km.

Capacity 6 violations of 6.9, 12.1, 3.2, 15.4, 6.4 and 2.7 kg.

Max. tour lenght 1 violation of 273.64 km.

a major constraint violation. Based on our analysis

we discovered that the 90% of the tours of the hand-

made solutions are not feasible according to some of

the constraints of the model. Conversely, our algo-

rithm always respects all constraints.

In conclusions, our algorithm, allows to save time

(30 minutes instead of 20 man-hours), to save money

(315’000 e/year), and it produce solutions with a

higher level of quality.

8 CONCLUSIONS

In this paper we have proposed an algorithm that hy-

bridizes heuristic and exact methods to solve the prob-

lem of a real-world distribution logistic company. Our

algorithm combines three existing optimization tech-

niques (Ant Colony Optimization, Column Genera-

tion and Mixed Integer Programming) with an in-

cremental search that improves the standard Column

Generation procedure. Our algorithm provides both

tight lower and good feasible solution in a reasonable

amount of time. We proved the effectiveness of our

algorithm and the beneﬁts of the devised incremen-

tal search solving 14 real-world instances. We have

proved the potential positive impacts deriving from

the application of the optimization algorithm to the

daily business of our industrial partner. Future work

consist in speeding up the algorithm to deliver valid

lower bounds in less time. In particular, we plan to

implement the Decremental State Space Relaxation

technique presented in (Righini and Salani, 2008).

Additionally, we intend to explore the option of per-

mitting constraint violation as this is currently done in

practice and to compare results against manual ones.

REFERENCES

Archetti, C., Savelsbergh, M. W. P., and Speranza, M. G.

(2006). Worst-case analysis for split delivery vehicle

routing problems. Transportation Science, 40:226–

234.

Archetti, C., Speranza, M., and Savelsbergh, M. (2008).

An optimization-based heuristic for the split deliv-

ery vehicle routing problem. Transportation Science,

42(1):22–31.

Baldacci, R., Christoﬁdes, N., and Mingozzi, A. (2008).

An exact algorithm for the vehicle routing problem

based on the set partitioning formulation with addi-

tional cuts. Mathematical Programming, 115:351–

385.

Ceselli, A., Righini, G., and Salani, M. (2009). A column

generation algorithm for a vehicle routing problem

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

254

with economies of scale and additional constraints.

Transportation Science, 43(1):56–69.

Desaulniers, G. (2010). Branch-and-price-and-cut for the

split-delivery vehicle routing problem with time win-

dows. Operations Research, 58:179–192.

Desrosiers, J., Pelletier, P., and Soumis, F. (1981). Plus

court chemin avec contraintes d’horaires. Montr

eal:

Universit

e de Montr

eal, Centre de recherche sur les

transports.

Doerner, K. and Schmid, V. (2010). Survey: Matheuristics

for rich vehicle routing problems. In Blesa, M., Blum,

C., Raidl, G., Roli, A., and Sampels, M., editors, Hy-

brid Metaheuristics, volume 6373 of Lecture Notes in

Computer Science, pages 206–221. Springer Berlin /

Heidelberg.

Dror, M. (1994). Note on the complexity of the shortest path

models for column generation in vrptw. Operations

Research, 42(5):977–978.

Gambardella, L. M., Taillard, E., and Agazzi, G. (1999).

Macs-vrptw: a multiple ant colony system for vehicle

routing problems with time windows. In New ideas

in optimization, pages 63–76. McGraw-Hill Ltd., UK,

Maidenhead, UK, England.

Golden, B., Raghavan, S., and Wasil, E. A. (2008). The ve-

hicle routing problem : latest advances and new chal-

lenges. Operations research/Computer science inter-

faces series, 43. Springer.

Nowak, M., Ergun, O., and White III, C. C. (2009). An

empirical study on the beneﬁt of split loads with the

pickup and delivery problem. European Journal of

Operational Research, 198(3):734–740.

Righini, G. and Salani, M. (2006). Symmetry helps:

Bounded bi-directional dynamic programming for the

elementary shortest path problem with resource con-

straints. Discrete Optimization, 3(3):255–273.

Righini, G. and Salani, M. (2008). New dynamic program-

ming algorithms for the resource constrained elemen-

tary shortest path problem. Netw., 51:155–170.

Rizzoli, A., Montemanni, R., Lucibello, E., and Gam-

bardella, L. (2007). Ant colony optimization for real-

world vehicle routing problems. Swarm Intelligence,

1(2):135–151.

Ruinelli, L. (2011). Column generation for a rich vrp.

Master’s thesis, Department of Innovative Technolo-

gies, SUPSI, Manno, Scuola universitaria profes-

sionale della Svizzera italiana, Galleria 2, CH-6928

Manno.

Salani, M. and Vacca, I. (2011). Branch and price for the

vehicle routing problem with discrete split deliveries

and time windows. European Journal of Operational

Research, 213(3):470–477.

Salari, M., Toth, P., and Tramontani, A. (2010). An ilp

improvement procedure for the open vehicle rout-

ing problem. Computers and Operations Research,

37(12):2106–2120.

Schmid, V., Doerner, K. F., Hartl, R. F., Savelsbergh, M.

W. P., and Stoecher, W. (2009). A hybrid solution

approach for ready-mixed concrete delivery. Trans-

portation Science, 43(1):70–85.

Sharda, R., Vo, S., Archetti, C., and Speranza, M. G.

(2008). The split delivery vehicle routing problem:

A survey. In Golden, B., Raghavan, S., and Wasil,

E., editors, The Vehicle Routing Problem: Latest Ad-

vances and New Challenges, volume 43 of Operations

Research/Computer Science Interfaces Series, pages

103–122. Springer US.

Toth, P. and Vigo, D. (2002). The vehicle routing prob-

lem. SIAM monographs on discrete mathematics and

applications. Society for Industrial and Applied Math-

ematics.

Wolsey, L. (1998). Integer programming. Wiley-

Interscience series in discrete mathematics and opti-

mization. Wiley, New York, NY, USA.

HYBRID COLUMN GENERATION-BASED APPROACH FOR VRP WITH SIMULTANEOUS DISTRIBUTION,

COLLECTION, PICKUP-AND-DELIVERY AND REAL-WORLD SIDE CONSTRAINTS

255