A HEART RATE PREDICTION MODEL FOR THE

TELEREHABILITATION TRAINING OF CARDIOPULMONARY

PATIENTS

Axel Helmer

, Riana Deparade

, Friedrich Kretschmer

, Okko Lohmann

, Andreas Hein

Michael Marschollek

and Uwe Tegtbur

R&D Division Health, OFFIS Institute for Information Technology, Escherweg 2, D-26121, Oldenburg, Germany

Institute of Sports Medicine, Medical School Hannover, Carl-Neuberg-Strasse 1, D-30625, Hannover, Germany

Computational Neuroscience, University of Oldenburg, Carl-von-Ossietzky-Strasse 9-11, D-26129, Oldenburg, Germany

Peter L. Reichertz Institute for Medical Informatics, University of Braunschweig - Institute of Technology and Hannover

Medical School, Mühlenpfordtstr. 23, D-38106 Braunschweig and Carl-Neuberg-Str. 1, D-30625, Hannover, Germany

Keywords: Modeling, Heart rate, Prediction, Cardiopulmonary rehabilitation.

Abstract: Chronic obstructive pulmonary disease (COPD) and coronary artery disease are severe diseases with

increasing prevalence. They cause dyspnoea, physical inactivity, skeletal muscle atrophy and are associated

with high costs in health systems worldwide. Physical training has many positive effects on the health state

and quality of life of these patients. Heart Rate (HR) is an important parameter that helps physicians and

(tele-) rehabilitation systems to assess and control exercise training intensity and to ensure the patients’

safety during the training. On the basis of 668 training sessions (325 F, 343 M), demographic information

and weather data, we created a model that predicts the training HR for these patients. To allow prediction in

different use cases, we designed five application scenarios. We used a stepwise regression to build a linear

model and performed a cross validation on the resulting model. The results show that age, load, gender and

former HR values are important predictors, whereas weather data and blood pressure just have minor

influence. The prediction accuracy varies with a median root mean square error (RMSE) of ≈11 in scenario

one up to ≈3.2 in scenario four and should therefore be precise enough for the application scenarios

mentioned above.

1 INTRODUCTION

1.1 Background

Patients with chronic obstructive pulmonary disease

(COPD) are suffering from the consequences of a

chronic inflammation of their pulmonary system.

This leads to an obstruction of the bronchi that

causes airflow limitation and shortness of breath.

Often, immobility and social isolation are the

consequences, which in turn reinforce the

degeneration of muscle mass and aggravate the

symptoms. The Global Initiative for Chronic

Obstructive Lung Disease (GOLD) summarizes:

“COPD is the fourth leading cause of death in the

world and further increases in its prevalence and

mortality can be predicted in the coming decades”

(Rodriguez-Roisin and Vestbo, 2009). Just the direct

medical costs attributable to COPD were estimated

at $49.5 billion in the US (Lung Institute, 2009) and

€38.6 billion in the European Union (Simon et al.,

1990) for 2010.

Beside the pharmacological treatment, an

important part of therapy is regular endurance

training. Pulmonary rehabilitation training improves

physical capacity, reduces breathlessness, reduces

the number of hospitalizations and increases the

quality of life (Rodriguez-Roisin and Vestbo, 2009).

1.2 Related Work

Achten and Jeukendrup summarized current research

achievements in the field of heart rate monitoring in

2003 and state: “…the most important application of

Helmer A., Deparade R., Kretschmer F., Lohmann O., Hein A., Marschollek M. and Tegtbur U..

A HEART RATE PREDICTION MODEL FOR THE TELEREHABILITATION TRAINING OF CARDIOPULMONARY PATIENTS.

DOI: 10.5220/0003713800300036

In Proceedings of the International Conference on Health Informatics (HEALTHINF-2012), pages 30-36

ISBN: 978-989-8425-88-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

HR monitoring is to evaluate the intensity of the

exercise performed” (Achten and Jeukendrup, 2003).

They conclude that the important influence factors

on HR are age, gender, environmental temperature,

hydration and altitude. They estimated the day-to-

day variance under controlled conditions to be 2-4

beats per minute (bpm).

Velikic et al. used data from an accelerometer for

a comparison of different models (linear, non-linear,

Kalman filter) for HR prediction of healthy subjects

and such with congestive heart failure (Velikic et al.,

2010). The two linear models delivered the best

results for a short term prediction of 20 minutes. Su

et al. introduced a model to control HR during

treadmill exercise (Su et al., 2006). Further

approaches for the same application were provided

by Cheng et al. (Cheng et al., 2008) and Mazenc et

al. (Mazenc et al., 2010). Neither have any of these

models been checked for their applicability to

cardiopulmonary patients nor do specialized HR

models exist for these.

1.3 Aim and Scope

Heart rate is an important vital parameter and

thereby an important indicator of a patients physical

state during rehabilitation trainings (Song et al.,

2010). The knowledge about factors that have an

influence on the exercise physiology might help

physicians to take this information into account

when deciding how much load a patient can undergo

during a training session. Hence it could be used to

support creation and optimization of training

schedules and during the current training session

itself to derive the future course.

A difference between the predicted trend of a

normal training and a measured heart rate may give

a hint on a potentially abnormal development and

thereby help to detect critical states before they

occur. This is especially important in tele-

rehabilitation settings, when patient’s train under

unsupervised conditions at home (see (Helmer et al.,

2010); (Lipprandt et al., 2009)). Integrating

predictive models in systems for the planning and

execution of individualized trainings has the

potential to increase patient’s security during

rehabilitation.

The aim of our research, which is presented in

this paper, is to introduce a model which predicts the

patients HR on the basis of given information about

the patient and the environment.

2 METHODS

2.1 Population, Data Acquisition and

Preparation

The data was obtained during outpatient

rehabilitation from cardiopulmonary patients with

NYHA 1-2 and COPD level 2-3. The only exclusion

criterion was the inability to perform training.

We started with an original dataset of 164

patients (82 W, 82 M) and 1201 training sessions,

which were collected between July and September

2009 in the exercise training center of the Medical

School Hannover in addition to regular ambulatory

training sessions. Patients performed their sessions

twice a week, whereas in mean each patient

performed ~8 training sessions (± 7.7). HR was

obtained on the basis of electrocardiogram (ECG)

data. The following additional data were available:

 Patient demographics: age, sex

 Training data: date and time, duration, load

 Vital signs data: resting HR before training,

recovery HR after training, blood pressure (BP)

(rest, load, recovery – systolic and diastolic), Borg

value (Borg, 1970) (used scale 6-20), HR during the

whole training (sample rate ≈ 1 Hz.).

Figure 1: Sample training session with heart rate, training

load and distinction into the four training phases.

We also included environmental variables, which

could have a possible influence. For this purpose we

procured data from the German weather service that

was recorded by a weather station in Hannover

(station id: 2014), where the training took place. We

chose temperature, humidity and air pressure as

main descriptors for weather and added them to the

training data.

Only fully completed training sessions with a

specific phase and full duration and a typical load

course showing the characteristics of a successful

A HEART RATE PREDICTION MODEL FOR THE TELEREHABILITATION TRAINING OF CARDIOPULMONARY

PATIENTS

four-phase rehabilitation training (see figure 1) were

included into the dataset. The first phase (warm up)

consists of a load plateau at a certain level. This load

increases stepwise over time in the second phase.

The third phase (load phase) shows a constant load

for at least 10 minutes. In the fourth phase (cool

down) the load is reduced stepwise until it reaches

null. We also excluded sessions, where a monitoring

physician interfered by de- or increasing the training

load, because the reasons of such changes were not

documented in our data. This could also be an

indicator for training under suboptimal conditions,

e.g. the training load was too high or low for the

patient due to an inadequately adapted training

schedule.

To automatically and robustly extract the

sessions from the dataset matching the previously

mentioned criteria, we calculated the difference

derivate of the load values over time to detect

whether the load was in- or decreasing during a

training session. Additionally, a session had to last

from 12 to 26 minutes in total. After discarding all

training sessions not fulfilling these criteria, we

reduced the above mentioned number of 1201 to 668

(325 F, 343 M) training sessions from 115 patients

(in mean 5.8± 4.5 trainings per patient).

2.2 Model Creation

For the integration of the predictive model into

existing training systems the set of potential

predictors (input variables which explain a

significant part of the response variable) varies

depending on the point in time and the use case.

We designed five different scenarios with

expanding/extending datasets, which take place in

settings of telerehabilitation training and during live

training in clinics. The first scenario describes a

situation before training when the schedule is

created, but no reliable weather forecast is available

(approximately three days before the training day).

The second scenario includes the weather forecast.

In the third scenario the patient already wears the

sensors, but the training has not yet been started. The

fourth scenario depicts an ongoing training and the

prediction includes data that was gathered during

previous completed training phases. To provide an

example, the average heart rate of the warm up

plateau phase can be included into the dataset for the

load phase. The fifth scenario describes the situation

after the training and does also include data like the

subjective perceived exertion of the patient

expressed on the Borg scale.

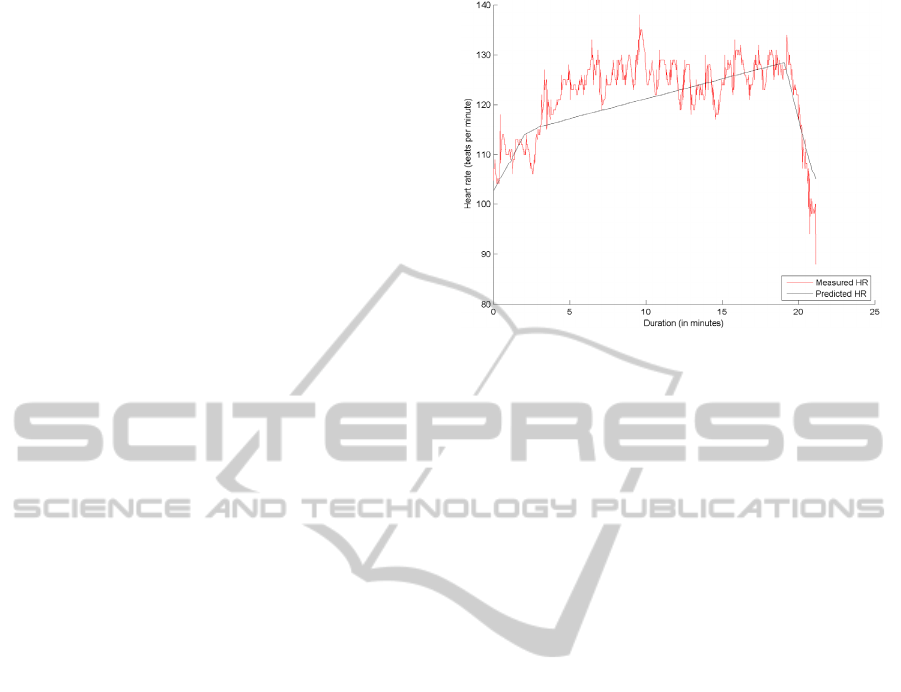
Figure 2: Sample training session for scenario four with

measured and predicted heart rate. The RMSE is

calculated for the four training phases.

The following list is sorted in ascending order by

the number of predictors available and the time in

relation to the training session. Each scenario

expands the predictor set of the previous one:

 Scenario S1 (training plan creation): patient

demographics and training plan data (load, duration

of each phase)

 Scenario S2 (training plan creation few days

before the training day): weather data

 Scenario S3 (at the beginning of the training):

resting HR, resting BP

 Scenario S4 (during the training): average HR of

the former phase, HR at the end of the former phase,

BP during the load phase (phase three)

 Scenario S5 (after the training): average HR of

current training phase, average HR of load phase,

average HR of all phases, recovery pulse, recovery

BP, average of all BP values, Borg value

The final list of predictors for scenario five included

24 items (see table 1).

To build a hypothesis about which values have a

relevant influence on the HR, we used a stepwise

regression analysis (Hair et al., 2006). This

algorithmic approach performs a multilinear

regression and determines a model, by adding or

removing the variable with the highest or lowest

correlation of the model’s F-statistics stepwisely.

So the variable with the highest chance of

explaining the variance of the given normally

distributed data set is added to the model, when the

correlation is big enough to reject the null

hypothesis. This is done until all variables with

significant influence (predictors) have been added

and all variables with non-significant influence have

been removed from the final model. We used the

HEALTHINF 2012 - International Conference on Health Informatics

standard entrance and exit tolerances of p ≤ 0.05 and

p ≥ 0.10 for the model. Additionally, we performed

chi-square tests to confirm the normal distribution of

the HR dataset.

The stepwise regression determines a set of

coefficients (B

) and an intercept (also called

constant term) (c) as result. Together with a number

of given predictor values (X

) it yields a linear

combination of the following form to calculate the

response variable (Y):

Y = c + b

+ b

... + b

(1)

We created such a submodel for each training phase

(warm up plateau, warm up ramp, training and cool

down) to reflect the different physiological targets.

These four submodels were then concatenated to a

complete model for one training session (see figure

2). This also simplified the comparison to the real

HR of the training sessions used for validation.

2.3 Model Evaluation

To determine the quality of our model and to prevent

overfitting, we performed a 2-fold cross-validation.

We divided the dataset into two parts d

and d

. Both

parts were of the same size and contained randomly

selected training sessions (n=334) from the dataset.

First, we used d

to train the model and validated it

against the d

dataset then we performed this

procedure vice versa.

We calculated the root mean square error

(RMSE) which quantifies the deviation between

measured and predicted heart rate over a whole

training.

It is not easy to determine, which predictor of the

resulting model explains which part of the response

variable, as each added predictor depends on the

former one. To make a statement about the influence

of the predictors, we measured the percental

improvement of the RMSE when a predictor is

added to the model in relation to the former one.

3 RESULTS

We modeled the four stages of a training session

(one for each training phase) for the five different

scenarios and determined the weighted RMSE to

quantify the error of each model (see figure 2).

Table 1 shows the contribution of different

predictors to the model and their effect on the

RMSE. Because of their naturally high correlation

(also known as multicollinearity) it is no surprise

Table 1: Mean contribution of the predictors on the scenario (S1-S5) model. All values represent the improvement of the

former RMSE in percent by addition of a predictor during stepwise regression. The “-” symbol denotes that a predictor is

not available in the given scenario. The calculated average influence of a predictor is shown in column “Overall”. The order

of these values is additionally illustrated by a rank order in the last column.

Predictor S1 S2 S3 S4 S5 Overall Rank

Age 11.032 11.032 11.1115 9.002 8.018 10.0391 3

Gender 0.754 0.754 0.745 0.1555 0 0.4817 8

Load 0.368 0.368 5.5555 0.646 0.0775 1.403 6

Overall training duration 0.0645 0.0645 0 0 0 0.0258 12

Duration of current training phase 0.0395 0.0395 0.015 0.019 0.0105 0.0247 13

Air pressure - 0.0265 0.0125 0.141 0.1355 0.078875 11

Temperature - 0 0 0 0 0 -

Humidity - 0 0 0.0585 0 0.014625 14

Resting HR - - 40.9895 7.1535 5.268 17.8036667 2

Resting BP systolic - - 0.494 0.118 0.119 0.24366667 9

Resting BP diastolic - - 0 0 0.0855 0.0285 11

Average HR of former phase - - - 57.0635 54.3 55.68175 1

Load phase BP systolic - - - 0 0.005 0.0025 16

HR at the end of former phase - - - 0 0.0265 0.01325 15

Load phase BP diastolic - - - 0 0 0 -

Average HR of current phase - - - - 5.648 5.648 4

Average HR of load phase - - - - 3.5475 3.548 5

Recovery pulse - - - - 0.6825 0.683 7

Recovery BP diastolic - - - - 0.122 0.122 10

Borg value - - - - 0 0 -

Average HR of all phases - - - - 0 0 -

Average of all BP values systolic - - - - 0 0 -

Average of all BP values diastolic - - - - 0 0 -

Recovery BP systolic - - - - 0 0 -

Total number of predictors 5 8 11 15 24

A HEART RATE PREDICTION MODEL FOR THE TELEREHABILITATION TRAINING OF CARDIOPULMONARY

PATIENTS

that four of the first five predictors have a high

impact on the model. Important other predictors are

age and load (Overall>1.4). The only predictor from

the weather data is the air pressure with just a very

small influence of ≈0.08%. Most of the different

blood pressure values and the Borg value have no

impact on the model.

Table 2 shows the accuracy of the prediction. For

the calculation of average and median over the

complete training the phases are weighted by their

duration.

The RMSE for scenario S1 and S2 is similar

(mean ≈12.3 and median ≈11.1). This also shows

that the available weather data has nearly no effect

on HR prediction. With an average HR of ≈98.4

bpm over all training sessions, this is equivalent to a

relative mean error of ≈12.5%. The third scenario

shows an average and median error of ≈8.5 and ≈6.1

which corresponds to a relative mean error of

≈8.6%. The difference between the average and

mean error suggests that there are some outlier

trainings that have a strong influence on the average

error.

Due to the additional predictors in S3, the

median error is almost reduced to 50% compared to

S2. The main reason for this strong improvement is

one dominating predictor: the resting heart rate (see

table 1). The overall ranking of this predictor is

dominated by its S3 value of ≈41%. This strongly

increases the average value where the values are

much lower in S4 (≈7.2%) and S5 (≈5.3%). This

might be caused by the dependence between resting

HR and the average HR of the former phase. The

latter seems to be the better predictor.

S3 is also the scenario in which the training load

has by far the highest influence (≈5.6%) with a

distance of 5% to the next smaller value in S4

(≈0.6%). A plausible explanation for this value

might be that training sessions with

cardiopulmonary patients are generally conducted at

a very low load of ≈35 watt on cycle ergometers.

Therefore the leg movement might have a stronger

influence on the real training load, than the selected

load of the bicycle ergometer.

S4 / S5 are further increasing the precision of the

prediction (mean ≈4.7 / ≈4.9, median ≈3.2 / ≈3.5 in

table 2) with an average relative error of ≈4.8% /

≈5%. This is mainly caused by time-near HR-based

values (average HR of former ≈55.7% and current

phase ≈5.6%).

Although more predictors contribute to scenario

S5 a higher prediction error is calculated compared

to S4, whereas it was vice versa during the model

building process (≈1.56 improvement for the mean

and

≈0.93 for the median RMSE). This is an

indicator for overfitting of the S5 model, which

might occur due to the usage of too many

explanatory variables.

4 DISCUSSION

The stepwise regression algorithm leads to a local

optimum which is not necessarily the global

optimum. A stepwise addition of variables decreases

the models’ RMSE. When using only the RMSE as

an indicator for the degree of influence for each

individual predictor this has the disadvantage, that a

later added predictor may have less influence,

because a part of his improvement is already

explained by the previously added variable. Thereby

the result depends on the order of the steps and

could lead to a suboptimal model when applied to

highly correlated variables (like systolic and

diastolic BP).

Therefore a stepwise regression can never

replace expert knowledge. On a statistical level, we

want to improve the model by performing a factor

analysis that will reduce the number of predictors

and provide a better knowledge about their

correlation to each other. This might also eliminate

the potential overfitting of S5 and enable the transfer

to other training modalities.

The accuracy of our model strongly depends on

the scenario and the associated data items. The first

scenario takes place during the training plan creation

and the calculated model shows the highest error.

This result might still be good enough to gain an

impression about HR development of a common

cardiopulmonary patient during training time. We

believe that the error of this scenario can be

improved by adding further predictors related to the

Table 2: Mean error of the prediction. All values refer to the RMSE of the model in relation to the real HR.

Scenario Phase 1 Phase 2 Phase 3 Phase 4 Average Median

11.448 10.267 12.079 12.954 12.254 11.069

11.443 10.267 12.079 12.986 12.260 11.084

5.528 6.514 8.528 9.561 8.498 6.068

4.347 3.636 4.637 6.572 4.733 3.266

4.762 2.940 4.734 5.281 4.906 3.542

HEALTHINF 2012 - International Conference on Health Informatics

patients metabolic response like weight, medication

and information about the current training state.

The available weather data only had a minor

influence and lowers the precision of the model.

This may reflect the fact that weather has no direct

influence on the patient when he trains in a tempered

environment. However, that does not mean that the

direct environment has no influence at all. We want

to examine this by the measurement of the

conditions inside the training area. Furthermore we

are going to examine if the weather indirectly affects

the Borg value, another very important value to

control the intensity of the rehabilitation training.

The influence of the resting HR at the beginning

of a training in S3 leads to a good precision of the

model during the training itself. This predictor is

probably influenced by many other, hard to measure

variables like medical treatment, stress, dehydration

and coffee consumption, which might have a strong

impact on the metabolic system. This leads to the

unexpected observation that the given blood

pressure values show only a very small effect on the

HR. Blood pressure kinetics are in close relationship

to HR, but not to absolute values, due to

antihypertensive treatment in most patient’s.

The prediction can be used to estimate the

patient’s physical state on the day of testing and

thereby help to define an appropriate training

intensity before the training starts.

The phase-wise prediction in S4 during the

runtime of the training shows a relative error below

5%. This should be precise enough to robustly detect

abnormal HR developments and calculate the

optimal load for the next phase. In future we will

focus on the analysis of other time dynamic

predictors that might increase the model accuracy

and also facilitate high refresh rates without the

abstract distinction between training phases.

5 CONCLUSIONS

We created a statistical model to predict HR as an

important vital parameter for the rehabilitation

training of cardiopulmonary patients. We considered

demographic data, training plan information, other

vital parameters and weather information as

potential predictors and classified them into five

aim-specific scenarios. The validation of the model

revealed that weather and the measured blood

pressure have nearly no direct influence on HR. Age

and previously measured HR based variables like the

resting HR strongly influence the responding HR.

The model exhibits an overall low error of ≈11

bpm in median, when used for the creation of a

training schedule (scenario 1). The error is reduced

by about 50%, when the model is used for prediction

at the beginning of a training session. The error

decreases below a significance level when the model

is used during a training to predict HR at the

beginning of each of the four training phases. This

makes it potentially suitable to detect critical

situations before they appear.

The precision of the prediction might be

improved by additionally including expert

knowledge and further statistical methods, but it

already serves as a good basis for the integration of

HR predictive mechanisms into training related

systems and might potentially increase the safety

and efficiency during the rehabilitation training of

cardiopulmonary patients.

ACKNOWLEDGEMENTS

This work was funded in part by the Ministry for

Science and Culture of Lower Saxony within the

Research Network “Design of Environments for

Ageing” (grant VWZN 2420/2524).

REFERENCES

Achten, J., Jeukendrup, A. E., 2003. Heart rate

monitoring: applications and limitations. Sports Med,

33(7):517–538.

Borg, G., 1970. Perceived exertion as an indicator of

somatic stress. Scandinavian journal of Rehabilitation

Medicine, 2(2):92–98.

Cheng, T. M., Savkin, A. V., Celler, B. G., Su, S. W.,

Wang, L., 2008. Nonlinear modeling and control of

human heart rate response during exercise with

various work load intensities. IEEE J BME,

55(11):2499–2508.

Hair, J. F., Black, W. C., Babin, B. J., Anderson, R. E.,

Tatham, R. L., 2006. Multivariate data analysis.

Pearson/Prentice Hall, Upper Saddle River, NJ, 6. ed.

edition. ISBN 0-13-032929-0.

Helmer, A., Song, B., Ludwig, W., Schulze, M.,

Eichelberg, M., Hein, A., Tegtbur, U., Kayser, R.,

Haux, R., Marschollek, M., 2010. A sensor-enhanced

health information system to support automatically

controlled exercise training of COPD patients. In

Pervasive Computing Technologies for Healthcare

(Pervasive Health), 2010 4th International Conference

on, pages 1 – 6.

Lipprandt, M., Eichelberg, M., Thronicke, W., Kruger, J.,

Druke, I., Willemsen, D., Busch, C., Fiehe, C., Zeeb,

E., Hein, A., 2009. OSAMI-D: An open service

A HEART RATE PREDICTION MODEL FOR THE TELEREHABILITATION TRAINING OF CARDIOPULMONARY

PATIENTS

platform for healthcare monitoring applications. In

Proc. 2nd Conference on Human System Interactions

HSI ’09, pages 139–145.

Lung, N. H. Institute, 2009. Morbidity & Mortality: 2009

Chart book on Cardiovascular Lung and Blood

Diseases. U.S. Department of Health and Human

Services National Institutes of Health.

Mazenc, F., Malisoff, M., de Queiroz, M., 2010. Model-

based nonlinear control of the human heart rate during

treadmill exercising. In Proc. 49th IEEE Conference

Decision and Control (CDC), pages 1674–1678.

Rodriguez-Roisin, R., Vestbo, J., 2009. Global Strategy

For The Diagnosis, Management, and Prevention Of

Chronic Obstructive Pulmonary Disease. Report.

Simon, P., Schwartzstein, R., Weiss, J., Fencl, V.,

Tegtsoonian, M., 1990. Distinguishable types of

dyspnea in patients with shortness of breath. Am Rev

Respir Dis, 142(5):1009–14.

Song, B., Wolf, K., Gietzelt, M., Al Scharaa, O., Tegtbur,

U., Haux, R., Marschollek, M., 2010. Decision support

for teletraining of copd patients. Methods Inf Med.,

49(1):96–102.

Su, S. W., Wang, L., Celler, B. G., Savkin, A. V., Guo, Y.,

2006. Modelling and control for heart rate regulation

during treadmill exercise. In Proc. 28th Annual Int.

Conference of the IEEE Engineering in Medicine and

Biology Society EMBS ’06, pages 4299–4302.

Velikic, G., Modayil, J., Thomsen, M., Bocko, M.,

Pentland, A., 2010. Predicting heart rate from activity

using linear and non-linear models. In Proceedings of

2011 IEEE 13th International Conference on e-Health

Networking, Applications and Services.

HEALTHINF 2012 - International Conference on Health Informatics