MULTILEVEL UNIT COMMITMENT IN SMART GRIDS

Maurice G. C. Bosman, Albert Molderink, Vincent Bakker, Gerard Smit and Johann L. Hurink

Dept. of Electrical Engineering, Mathematics and Computer Science, University of Twente, Enschede, The Netherlands

Keywords:

Unit commitment, Smart grids, Column generation.

Abstract:

This paper focuses on the planning of electricity resources in the developing electricity infrastructure. First we

model the existing infrastructure and extend this model to a smart grid infrastructure, where we focus on the

large scale introduction of small electricity generators, leading to generation possibilities at both ends of the

electricity network. Then the traditional Unit Commitment Problem (UCP) is given. We extend this formu-

lation to the Multilevel Unit Commitment Problem (MUCP), where we describe and include the possibilities

that arise in the developing smart grid, in a general way. Based on the characteristics of the problem with its

subdivision into different levels, a planning method for the MUCP is described. Finally we solve and analyze

a scenario, where a ﬂeet of 5000 houses is added to a small collection of power plants.

1 INTRODUCTION

The Unit Commitment Problem (UCP) (Sheble and

Fahd, 1994; Padhy, 2004) is the general term for a de-

cision problem that is related to energy generation. In

this problem, deterministic or stochastic energy de-

mand has to be supplied by a number of generators.

The UCP treats the commitment of speciﬁc genera-

tors during certain time windows (i.e. generators are

used to supply (part of) the demand or not) and deter-

mines the generation level of the committed genera-

tors in these time windows.

Traditionally the UCP origins from the situa-

tion where the demand is given as (deterministic or

stochastic) input (Kerr et al., 1966; Groewe-Kuska

and Roemisch, 2005). In the developing smart grid,

new technologies emerge in generation, storage and

consumption (see e.g. (United States Department of

Energy, 2003; Wemhoff and Frank, 2010; Alanne and

Saari, 2004; Lanzafame and Messina, 2010; Ayompe

et al., 2010; Arsie et al., 2009)). This leads to inter-

esting possibilities in demand side load management

and a change in the setting of the UCP. On the one

side, demand side load management gives possibili-

ties to shift demand, such that demand becomes part

of the decision making process rather than being used

as input data. On the other side, different types of

generation with their own characteristics are added to

the set of generators. Many small-sized generators are

distributed over the grid, which leads to a signiﬁcant

increase in the number of generators that are conside-

red in the UCP.

These advances in the energy supply chain lead to

a new formulation of the UCP, which we call the Mul-

tilevel Unit Commitment Problem (MUCP). Based on

the different sizes and locations in the infrastructure,

a multilevel element is added, taking into account

the quantitative impact of different generators or load

management. To solve this MUCP, the energy infras-

tructure is modeled and partitioned into various lev-

els. The MUCP is part of a three step control method-

ology for smart grids ((Molderink, 2011)) in which

the complete picture of the smart grid is captured: the

methodology consists of prediction, planning and re-

altime control.

The paper is organized as follows. In the next sec-

tion an overview of the energy infrastructure is given

and a model is presented for this structure. Then the

MUCP is formalized in Section 3. In Section 4 the

outlay of a planning method is sketched. As an exam-

ple, a comparison is made between a classic UCP and

the MUCP in Section 5. The results for this compari-

son are analyzed and discussed in Section 6.

2 THE ENERGY

INFRASTRUCTURE

In this section we model the energy infrastructure as a

ﬂow network. First the elements of the electricity grid

are introduced using a small example. Then the grid

is modeled using different elements for production,

361

G. C. Bosman M., Molderink A., Bakker V., Smit G. and L. Hurink J..

MULTILEVEL UNIT COMMITMENT IN SMART GRIDS.

DOI: 10.5220/0003716903610370

In Proceedings of the 1st International Conference on Operations Research and Enterprise Systems (ICORES-2012), pages 361-370

ISBN: 978-989-8425-97-3

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

consumption, transportation and communication.

The classic energy infrastructure (or supply chain)

can be clearly separated into a consumption and a pro-

duction side. Consumption of energy (gas, electricity,

heat, etcetera) can be predicted quite accurately, based

on historic demand and currently available charac-

teristics (of consumer behaviour, weather, etcetera)

(Bakker et al., 2010). In this classic situation, the

energy production of power plants is completely ad-

justed to match this demand. Through transmission

and distribution networks this production is brought

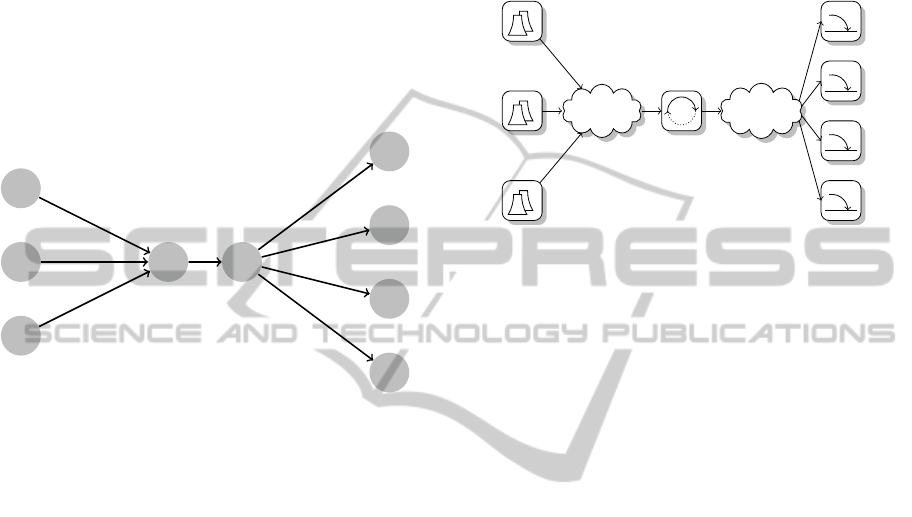
to the consumer. In Figure 1 a simpliﬁed example of

8|20

2|5

1|5

2|5

3|5

Figure 1: An example of the classic electricity infrastruc-

ture.

the situation in a certain time period is given, in which

a decision has to be made on the generation output of

three generators a, b and c, where demand is located

in f, g, h and i. The directed edges (e, f), (e, g), (e, h)

and (e, i) represent the distribution network. The ca-

bles in this part of the network have a certain demand

from the end points (e.g. villages, industrial areas)

and a ﬁxed network capacity for the given time pe-

riod, which are given as weights demand|capacity.

The aggregated demand of the end points f, g, h and i

has to be supplied by the transmission network, which

is represented by the directed edge (d, e). This de-

mand eventually has to be produced by the three gen-

erators, which have a different production capacity. In

this case, all demand can be supplied by generator b

alone, whereas a combination of generators has to be

committed when a or c is willing to produce, since

their production capacity is insufﬁcient to supply the

actual demand alone.

In the current ﬂow network of the example, there

is no bottleneck. Even if all end points would ask

maximum demand (i.e. a demand equal to the distri-

bution grid capacity), the transmission grid is able to

supply this amount of electricity, and the three gener-

ators can produce this amount. When the classic in-

frastructure changes into the new smart grid, the clas-

sic division into a production and a consumption side

becomes less clear. The original consumers also have

the possibility to produce, which results in a bidirec-

tional network. This might put more stress on the ex-

isting infrastructure. In this paper we assume that the

transmission/distribution capacity of the correspond-

ing networks is sufﬁcient even for extreme demands.

village

MV grid

transformer

HV grid

power plant

Figure 2: A model of the classic electricity infrastructure.

In Figure 2 the classic infrastructure of Figure 1

is modeled again, by using different types of nodes

to stress the differences between generation, trans-

portation and consumption. This model allows to

model ﬂows of different types, with preservation of

energy, as proposed by (Molderink, 2011). As indi-

cated in this model, we introduce additional nodes

compared to Figure 1, drawn as clouds, which rep-

resent the level of the grid. The power plants are con-

nected to the high voltage grid, which is connected

to the medium voltage grid, via a transformer. The

demand of the example is connected to this medium

voltage grid. In the Unit Commitment Problem, the

following challenge for the power plants has a cen-

tral position: how to supply the given demand by

the available generation possibilities, such that the

total generation is done under minimum operational

costs? Operational costs can be divided into energy

(fuel efﬁciency) and cost effective costs (maintenance

and startup/shutdown costs) (Sheble and Fahd, 1994;

Padhy, 2004).

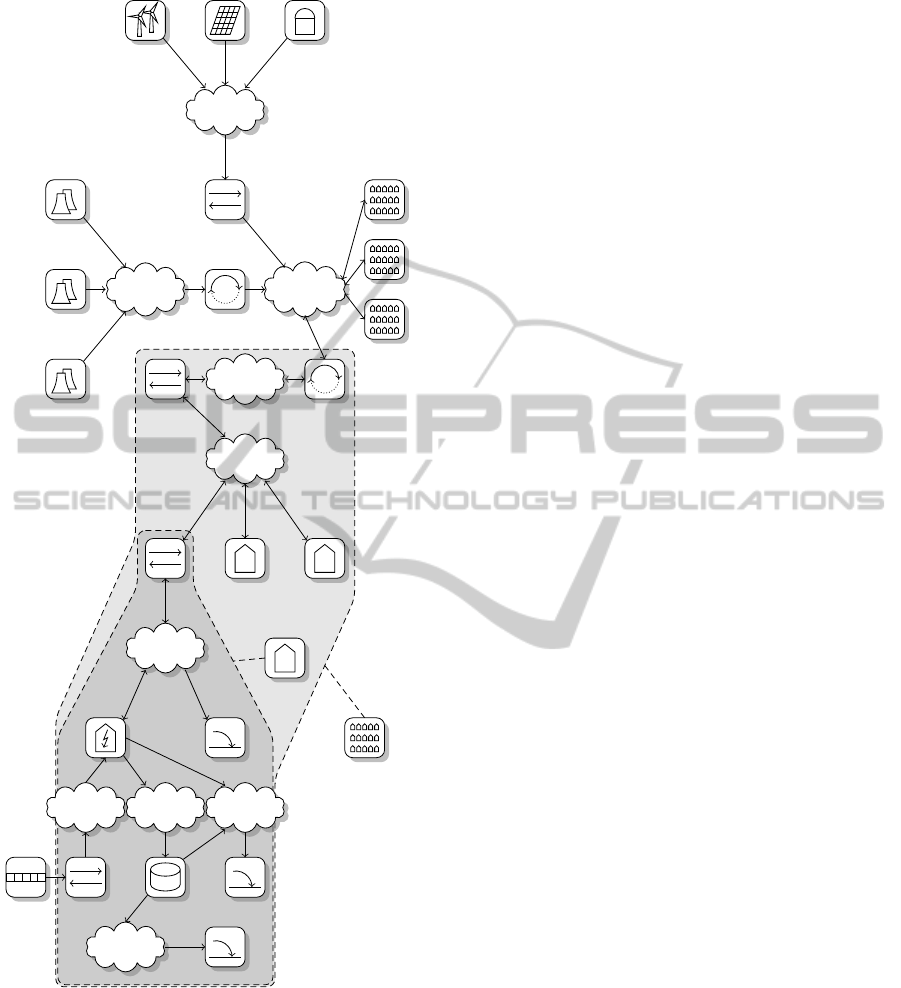
Figure 3 shows the extended infrastructure. As

in Figure 2, directed edges show the electricity ﬂow

in the network. Some edges are bidirectional, in-

dicating that a ﬂow in both ways is possible. The

large power plants are connected to the high voltage

grid; smaller generation (e.g. windmill/solar panel

parks, biogas installations, etcetera) is connected to

the medium voltage grid. Note that this smaller gen-

eration is not directly coupled to the medium voltage

grid, but via an additional electricity node, which is

connected to an exchanging node, called ‘new gen-

eration’. This ‘exchanger’ expresses the introduction

of a new, lower level in the model of the smart grid

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

362

village

house

MV grid

transformer

HV grid

power plant

village

transformer

LV grid

village

electr.

house house house

electr.

local consumption

microCHP

gas

gas network

heat loss

heat buffer loss

heat

heat demand

new generation

windmill

solar panels biogas

electr.

Figure 3: A model of the smart grid infrastructure.

and functions as a separator between the optimization

problem on the higher level and the local commitment

problem on the lower level (e.g. the smaller genera-

tion). The exchanger can be seen as a communication

means between higher and lower order planning prob-

lems. This division into levels is further explained in

Section 4.

Compared to the model of Figure 2, areas like vil-

lages are now modeled in more detail. In the previ-

ous model it sufﬁced to consider the connection of a

village to the medium voltage grid, since only aggre-

gated demand is taken into account. In the extended

model a village is connected to the lower voltage grid

and an exchanger is used to specify a lower level.

In this lower level, a next level is introduced for the

houses to model their own generation/consumption

characteristics. Within the model (e.g. within the

houses) different types of energy (i.e. gas and heat)

are combined. This is one of the strengths of the ex-

tended model. In the model presented in Figure 3 we

show the modeling of a microCHP (Combined Heat

and Power generation on a household level (United

States Department of Energy, 2003)), which is a de-

vice that consumes natural gas and produces both heat

and electricity at a ﬁxed ratio. It is convenient to use

a heat buffer next to this microCHP to guarantee the

heat supply in the house and to partially decouple heat

consumption from the generation of heat (and elec-

tricity). In the model, gas import information is stored

in the gas exchanger. The energy efﬁciency of gener-

ation can be modeled by adding energy losses. In the

example, the loss ﬂow of the microCHP has a ﬁxed ra-

tio to the heat and electricity generation; the loss ﬂow

of the heat buffer is determined by the state of the

buffer. In a similar way, the efﬁciency of each type

of generation can be modeled. However, for simplic-

ity this is left out of Figure 3 and we do not consider

efﬁciency in the remainder of this paper.

3 THE MULTILEVEL UNIT

COMMITMENT PROBLEM

This section describes the Multilevel Unit Commit-

ment Problem. Starting from the Unit Commitment

Problem we derive additional constraints to formulate

the MUCP.

The classic UCP aims to minimize operational

costs or to maximize the proﬁt of the system of gener-

ators. We consider the problem of minimizing costs.

Operational costs are depending both on the binary

commitment variables u

i, j

(specifying whether gener-

ator i is committed or not in time period j) and on the

production level x

i, j

(specifying the electricity pro-

duction of generator i in time period j). In general

the operational costs can be described by a function

f(u, x), where the variables u and x run over the time

horizon T for N generators. Note that startup costs

are incorporated in this notation. The objective of the

UCP is then to minimize f(u, x). Some common con-

straints that are mostly used in the UCP are given in

formulation (1)-(9).

MULTILEVEL UNIT COMMITMENT IN SMART GRIDS

363

min f(u, x) (1)

s.t.

∑

i, j

≥ d

∀ j (2)

∑

i, j

max

− x

i, j

) ≥ r

∀ j (3)

i, j

min

≤ x

i, j

≤ u

i, j

max

∀i, j (4)

down

≤ x

i, j

− x

i, j−1

≤ s

∀i, j (5)

i, j

≥ u

i, j−k

− u

i, j−k−1

∀i, j, k = 1, . . . , t

− 1 (6)

1− u

i, j

≥ u

i, j−k−1

− u

i, j−k

∀i, j, k = 1, . . . , t

− 1 (7)

i, j

∈ {0, 1} ∀i, j (8)

i, j

∈ R

∀i, j (9)

Equation (2) requires that the total production sat-

isﬁes the total demand; equation (3) asks for a cer-

tain amount of spinning reserve r

, i.e. the additional

available generation capacity of already committed

generators. This constraint is added to guarantee a

certain amount of ﬂexibility in the case of a higher-

than-predicted demand or in the case of a failure of a

certain generator. The production boundaries of the

generators x

min

and x

max

are deﬁned in equation (4)

and the ramp up and ramp down rates s

and s

down

which determine the speed with which generation can

be adjusted, are given in equation (5). Equations (6)

and (7) state that the generator has to stay up and run-

ning (or stay switched off) once a corresponding deci-

sion to switch it on (or off) has been made within the

last t

) time periods. The decisions to commit a

generator are binary decisions, where the production

decisions are real numbers.

When we consider the developing energy infras-

tructure, we see more decentralized energy produc-

tion y

m, j

, where y

m, j

speciﬁes the electricity produc-

tion of local generator m in time period j. The maxi-

mum production of these types of generators is much

smaller than the minimum production of a power

plant: max

max

) ≪ min



min



. However, there

may be very many of them. The local generators

are often more limited in their production decisions

than normal power plants, especially when we con-

sider combined heat and electricity generation (e.g.

micro/mini Combined Heat and Power). In this case

the heat demand of the local household/glasshouse

determines to a large extent the total daily generation,

where some ﬂexibility is provided by the use of a heat

buffer. Also, the power output is completely deter-

mined for many of these generators, once the gener-

ator is in operational mode. This further limits the

ﬂexibility of the decision maker.

In the developing energy infrastructure, also a lot

of renewable generation is introduced, which more

and more takes place on a local scale. To cope with

these changes we extend the given UCP formulation

in the following way to a MUCP formulation.

min f(u, x)− g(p, u, y) (10)

s.t.

∑

i, j

∑

m, j

≥ h

(d) ∀ j (11)

∑

i, j

max

− x

i, j

) ≥ r

∀ j (12)

min

j,F

≤

∑

m∈F

∑

k=1

m,k

≤ z

max

j,F

∀ j, n (13)

i, j

min

≤ x

i, j

≤ u

i, j

max

∀i, j (14)

down

≤ x

i, j

− x

i, j−1

≤ s

∀i, j (15)

i, j

≥ u

i, j−k

− u

i, j−k−1

∀i, j, k = 1, . . . , t

− 1 (16)

1− u

i, j

≥ u

i, j−k−1

− u

i, j−k

∀i, j, k = 1, . . . , t

− 1 (17)

m, j

≥ u

m, j−k

− u

m, j−k−1

∀m, j, k = 1, . . . , t

− 1 (18)

1− u

m, j

≥ u

m, j−k−1

− u

m, j−k

∀m, j, k = 1, . . . , t

− 1 (19)

min

m, j

≤

∑

k=1

m,k

≤ y

max

m, j

∀m, j (20)

m, j

= l(u

) ∀m, j (21)

i, j

, u

m, j

∈ {0, 1} ∀i, m, j (22)

i, j

, y

m, j

∈ R

∀i, m, j (23)

The formulation of the MUCP is given by equations

(10)-(23), where the original UCP can be found in

equations (11),(12) and (14)-(17). In this MUCP

model we also incorporate demand side load manage-

ment to alter the demand. This is formalized in equa-

tion (11) by the function h

(d). Furthermore, the lo-

cal generation y

m, j

is taken into account in this equa-

tion too. The local generators have the same type of

dependency constraints on runtime and offtime over

time periods (equations (18) and (19)) as the large

generators (equations (16) and (17)). Next to these

machine dependency constraints the generators also

have user dependencies, resulting e.g. from the heat

demand. The use of a heat buffer, with some ini-

tial heat level, in combination with the local heat de-

mand, determines the minimum aggregated heat pro-

duction and the maximum aggregated heat produc-

tion. Since heat and electricity production are directly

coupled, we model this relationship using a minimally

required aggregated electricity production y

min

m, j

and a

maximally allowed aggregated electricity production

max

m, j

, as in equation (20). So, possible decisions in

future intervals are not only inﬂuenced directly via

runtime/offtime constraints, but they are also inﬂu-

enced indirectly via equation (20). As stated before,

the generator output is completely determined by the

commitment decisions, as in equation (21).

The planning problem for only a group of mi-

croCHPs is proven to be NP-complete in the strong

sense, due to the two-dimensional aspect of the prob-

lem (i.e. a strong dependency between generation in

time periods and a strong dependencybetween house-

holds due to the aggregated generation in the ﬂeet)

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

364

(Bosman et al., 2010). It is therefore practically in-

tractable to solve the MUCP (of which the planning

problem for a ﬂeet of microCHPs is only a part of

the problem) directly. However, heuristics have been

developed to solve the planning problem for the ﬂeet

(Bosman et al., 2011). For this reason, a planning

method for the MUCP is presented that uses the natu-

ral division into different production levels to separate

the decisions that haveto be made for the power plants

and for the local generators, and still combine the two

into a global Multilevel Unit Commitment decision

problem.

In the MUCP, a group of local generators (called

a ﬂeet) is considered as one entity on the planning

level, equivalent to a power plant. Of course, a sub-

division in multiple entities F

is allowed. Equation

(13) is applied to these n ﬂeets, which forces the ag-

gregated production of all generators to be within up-

per and lower bounds z

max

j,F

and z

min

j,F

. The most natu-

ral bounds are z

max

j,F

∑

m∈F

max

m, j

and z

min

j,F

∑

m∈F

min

m, j

These bounds may be sharpened further, since not all

possible decision paths (sequences) within these nat-

ural bounds may be feasible. We explain this by giv-

ing two examples. As a ﬁrst example, the capacity of

the ﬂeet may be smaller than

∑

m∈F

max

m, j

−

∑

m∈F

min

m, j−1

which may result in a ﬂeet decision in time period j

that cannot be met by the individual generators. This

would require additional bounds on the production ca-

pacity of the ﬂeet entity.

However, even if the ﬂeet decision respects the ca-

pacity of the ﬂeet and if the ﬂeet decision path stays

within the natural bounds

∑

m∈F

max

m, j

and

∑

m∈F

min

m, j

, it

can be impossible to follow this decision path by the

individual generation, as shown in the second exam-

ple by Figure 4. Figure 4(a) and 4(b) show the possi-

ble decision paths within the natural bounds (the gray

area) for two households equipped with a microCHP;

Figure 4(c) shows the combined decisions, includ-

ing capacity constraints, for which the given decision

path in Figure 4(d) is impossible to follow. Although

the two generators may run simultaneously, indepen-

dently in the fourth or in the ﬁfth time period, it is

impossible to have the two generators running simul-

taneously in these time periods subsequently, due to

the limited possibilities for the second household in

the fourth and ﬁfth time periods. So, even when ca-

pacity constraints are added the natural bounds may

not result in a ﬂeet entity decision that is feasible for

the individual generators. This is the reason why the

natural bounds may be sharpened. Also, to guarantee

stability, especially within the distribution network,

additional constraints may be posted to the output of

time

total production

(a) Possible transitions of one microCHP.

time

total production

(b) Possible transitions of another microCHP.

time

total production

tions of the combination.

time

total production

(d) Construction of a bid pattern which is impossible

to follow.

Figure 4: A counterexample for the natural ﬂeet bounds.

MULTILEVEL UNIT COMMITMENT IN SMART GRIDS

365

ﬂeets of small generators.

Since the operation of the individual small gener-

ators is of minor importance in comparison with the

behaviour of the ﬂeet, we do not wish to minimize op-

erational costs for the ﬂeet(s). In the additional func-

tion g(p, u, y) in equation (10) the proﬁt of the ﬂeet is

maximized, when this ﬂeet operates, using the given

bounds, on an electricity market with prices p

4 A PLANNING METHOD FOR

THE MUCP

In Section 2 the smart grid is modeled using a divi-

sion into different levels. This division is based on

the amount of energy the different generators produce

and forms the base for a leveled approach to solve the

MUCP of Section 3. In this section, a sketch of a plan-

ning method is given, introducing patterns as building

blocks for the method.

Since it is practically intractable to combine the

commitment of large and small types of generation,

information on the smaller generation is aggregated

on a higher level by using the exchangers, as shown in

the previous sections. Each ﬂeet (e.g. village, wind-

mill park) is then considered as one entity, with some

global constraints based on the aggregated informa-

tion, and treated in this simpliﬁed form in the opti-

mization problem. Note that on this high level, local

constraints on the smaller generators are discarded in

the optimization problem. The objective function of

this high level optimization problem reﬂects the orig-

inal objectives; operational costs are minimized for

power plants and the common ﬂeet output is maxi-

mized for its proﬁt on an electricity market. The deci-

sion paths that result from the optimization of the high

level optimization problem for all entities (whether

power plants or ﬂeets) are called patterns. For a power

plant this pattern simply reﬂects the commitment (and

generation level) decisions that have to be made; for

a ﬂeet this pattern is the input for a new, lower level

optimization problem.

On the lower level a new optimization problem is

formed, which is to match the provided ﬂeet pattern

with the available individual generation possibilities

as good as possible. So, the objective is to minimize

the deviation from the (higher level) ﬂeet pattern. A

ﬂeet consisting of small generators can sometimes be

optimized using full knowledge about each genera-

tor (i.e. patterns can be derived directly for biogas

installations, windmill parks, etcetera, based on lo-

cal constraints on these types of generation). How-

ever, for a ﬂeet consisting of houses it is harder to

solve an overall optimization problem in reasonable

time, where the full details of all houses are consid-

ered, especially when the number of houses is large.

In this situation, a next level is introduced, using a

column generation approach to provide the ﬂeet opti-

mization problem with so-called house patterns. The

lower level optimization problem has to select indi-

vidual house patterns in order to allow the ﬂeet plan-

ner to ﬁnd a combination of patterns that minimizes

the deviation from the ﬂeet pattern. Based on infor-

mation from the solution of the higher level optimiza-

tion problem, a column generation technique is used

to extend the current pattern set for each house with

new promising patterns.

Once the ﬂeet patterns are locally optimized, the

resulting patterns of the ﬂeet planning problem that

minimize the deviation from the original ﬂeet pat-

terns, are now communicated back to the high level

optimization problem. Using this information, this

problem is solved again. This can be seen as a clas-

sic UCP with altered demand (and possibly altered

spinning reserve). If the result is not satisfying, addi-

tional constraints on the ﬂeet patterns can be added to

the original high level optimization problem, and the

complete process can be repeated.

5 CASE STUDY

To study the inﬂuence of generation on multiple lev-

els in the electricity grid, we set up a scenario with

two levels. We choose to use two levels, to see the in-

teraction between generators of different production

capacity in a direct way. In this illustrative example

we use 10 generators on the highest level, with a to-

tal production capacity of 15 MW. This capacity is

divided over 5 generators with a capacity of 1 MW

and a minimum production level of 0.5 MW, and 5

generators with a capacity of 2 MW and a minimum

production level of 1 MW. The (absolute) ramp up

and ramp down rates are equal to the minimum pro-

duction for each power plant. Between the maximum

and minimum production values the operator of the

generator has ﬂexibility to choose its power output,

once the unit is committed. The minimum runtime

and offtime are set to half an hour.

On the lowest level, we have 5000 houses con-

taining a generator, with a total capacity of 5 MW.

These generators are microCHPs (Combined Heat

and Power systems on a household scale) with a pro-

duction output of 1 kW. This power output is a direct

result from the decision to run the microCHP on a

certain moment in time. This means that there is no

ﬂexibility in the production level of committed units,

although ﬂexibility can be found in the moments in

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

366

time that the units are committed. However, these mo-

ments are further constrained by the heat demand in

the houses: the maximum production of the ﬂeet over

the planning horizon is 39.8 MWh and the minimum

production is 35.1 MWh, which is of the same order

of committing a power plant for a complete day. The

minimum runtime and offtime are again set to half an

hour.

In the scenario we deﬁne four use cases to study

the inﬂuence of introducing a ﬂeet of microCHPs in

the UCP. For each use case we use time periods of

30 minutes length; the commitment is planned for a

complete day, which comes down to 48 time periods.

The total daily demand is 114.2 MWh, with a peak of

8 MW and a base load of 2.5 MW. In this scenario

we do not consider demand side load management.

We require a spinning reserve of 2 MW at all time

periods. The objective function combines operational

costs for the power plants and proﬁt maximization for

the ﬂeet. The ﬁrst use case is based on real prices

from the APX day ahead market

. In the second use

case we multiply all prices with −1, which creates

artiﬁcial negative values, to compare to what extent

the ﬂeet would change its decisions. The third use

case uses artiﬁcial prices that correspond to the daily

electricity demand; the higher the demand, the higher

the price. This use case is deﬁned to verify if the ﬂeet

can behave in such a way that peak demand can be

decreased and the demand for the power plants can

be ﬂattened. The fourth use case is the opposite of the

third case, in the sense that prices are again multiplied

with −1; the higher the demand, the lower the price.

0 200 400

600

800 1,000

1,000

2,000

3,000

4,000

generation per 30 minutes (kWh)

costs

power plant 1|3|5 power plant 2|4

power plant 6|8|10 power plant 7|9

Figure 5: The operational cost functions of the power

plants.

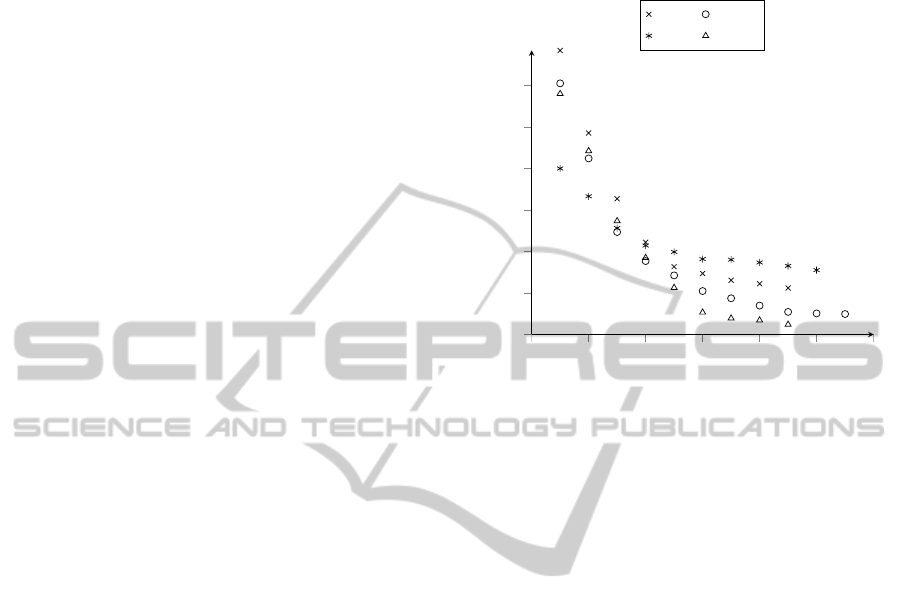
In Figure 5 the cost functions of the power plants

http://www.apxendex.com

are given. They are modeled as piecewise linear cost

functions, to approximate quadratic operational cost

functions. Below certain production levels (625 kWh

for the large power plants and 312.5 kWh for the

small power plants) the cost functions are equal, and

power plants are mutually exchangeable. The start of

a power plant is furthermore penalized with a cost of

1000.

The different optimization problems are mod-

eled as Integer Linear Programming formulations in

AIMMS modeling software using CPLEX 12.2 as

solver. The solution method is executed on a desk-

top computer (2.40 GHz and 2.00 GB RAM).

6 RESULTS AND DISCUSSION

In this section we discuss the solutions of the four use

cases, which are found by the planning method.

10 20 30 40

1,000

2,000

3,000

4,000

5,000

30 minutes intervals

generation (kWh)

power plant 1 power plant 2

power plant 3 power plant 4

power plant 5 power plant 6

power plant 7 power plant 8

power plant 9 power plant 10

local generation

Figure 6: The solution of the UCP.

Figure 6 shows the detailed solution of the UCP,

where we do not use the 5000 houses and the de-

mand is fullﬁlled against minimal operational costs.

The commitment and corresponding generation pat-

terns are given for the 10 power plants. This solution

is used to validate the optimization model. At any

time period, the spinning reserve of 1000 kWh (=2

MW for time periods of 30 minutes length) is avail-

able within this solution. The ramp rates are taken

into account; the minimum and maximum production

constraints are considered too. This can best be seen

when a generator shuts down. The time period before

MULTILEVEL UNIT COMMITMENT IN SMART GRIDS

367

a generator shuts down, the production is reduced to

the minimum production level, which happens to be

equal to the (absolute) maximum ramp up and ramp

down rates. In this case the generator may shut down

in the next period. We see that nine of the ten units are

committed during the day; each power plant is started

at most once.

Table 1 shows the results for the MUCP, where

we incorporate the ﬂeet of 5000 houses. The table

shows the operational costs of the power plants, both

for the initial planning with the rough ﬂeet constraints

(rough) and for the ﬁnal result after applying the col-

umn generation to the ﬂeet and replanning the power

plants using the elaborated ﬂeet pattern (result). It

also shows the number of starts for the power plants,

again for the rough planning and for the ﬁnal re-

sult. The computational time of the result includes the

computational time of the rough planning. Regard-

ing the ﬂeet planning, the ﬁnal mismatch to the rough

planning (i.e. absolute deviation from the rough plan-

ning) is given in kWh and in percentage of the total

generation of the rough planning. The resulting total

generation is given in the last row of Table 1. Since

we mostly use artiﬁcial prices for the electricity mar-

ket, we do not show the proﬁt maximization of the

ﬂeet in more detail.

The operational costs of the result are relatively

close to the rough planning operational costs in all

cases. This means that the commitment of the power

plants is not altered too drastically after the elaborated

planning of the ﬂeet; so, the planning method be-

havesas expected. Of course the ﬁnal costs are higher,

since the rough planning gives the optimal combina-

tion of power plant operation and ﬂeet operation. The

four use cases show that we are able to steer the ﬂeet

production by using different prices. The number of

starts of the power plants increases in all cases, ex-

cept for the third use case. In case 3 the power plants

need only 5 starts in the ﬁnal ﬂeet planning. This

is mostly due to the initial ﬂeet planning, which is

aimed to reduce the peaks in the demand. In the re-

alization of this planning the ﬂeet has relatively much

difﬁculties, since the mismatch from the rough plan-

ning is the highest of the four cases. Nevertheless this

realization leaves enough possibilities for the power

plants to ﬁnd a planning that only needs 5 commit-

ments. The big advantage is that the ﬂeet does not

interfere too much with the base load, which simpli-

ﬁes the continuity of the commitment in time periods

with low demand.

The computational time of the planning method

stays below half an hour in all cases. This is accept-

able for a practical application, especially since the

column generation technique can be distributed over

the smart grid in real life. The mismatch from the

rough planning is below 8%. Figure 7 shows the de-

0 2 4

8 10 12

0.2

0.4

0.6

0.8

1.2

·10

iterations

total mismatch (kWh)

case 1 case 2

case 3 case 4

Figure 7: The mismatch during the column generation for

the four use cases.

velopment of the mismatch during the column genera-

tion method. The ﬁnal solution is found after approxi-

mately 10 iterations. The existence of a mismatch can

be partly explained by a possible impractible rough

planning, but also by the fact that we used a maxi-

mum runtime of 60 seconds for the pattern matching

problem, which tries to select exacly one pattern for

each house to minimize the mismatch from the rough

planning. This maximum runtime results in a prelimi-

nary abortion of the solution method in all four cases.

From this we may conclude that the ﬂeet might have

done better, to the costs of higher computational time.

Finally we see that the total ﬂeet production approx-

imates the upper production bound of 39.8 MWh in

use cases 1, 3 and 4, whereas the total ﬂeet produc-

tion in case 2 is close to the lower production bound

of 35.1 MWh. This indicates that the prices in case 2

are too negative, such that it is more cost effective to

let the power plants produce more.

Figure 8 shows the unit commitment of the 10

power plants and the ﬂeet production of the 5000

houses in the second use case. Figure 8(a) gives the

rough ﬂeet planning and Figure 8(b) gives the result-

ing, ﬁnal ﬂeet planning. We show this use case in

more detail to describe two phenomena that occur.

Firstly, we see three short periods of commitment

of the small power plants 1 and 3 in the ﬁnal plan-

ning. These commitments are not necessary to full-

ﬁll the demand; the already committed power plants

could have supplied this additional demand them-

selves, even against lower costs. However,in that case

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

368

Table 1: MUCP results for the four cases.

case 1 case 2 case 3 case 4

rough detailed rough detailed rough detailed rough detailed

operational costs 158748 164846 163593 169325 154748 163230 154748 167730

# of starts

5 6 5 8 5 5 5 9

computational time (s) 32.28 1543.10 26.91 1798.19 61.72 1753.56 7.40 1451.00

mismatch (kWh) 2236.5 986 3099.5 478.5

mismatch/rough prod. (%)

5.6 2.8 7.8 1.2

ﬂeet production (kWh) 38926 35589 37927 38868.5

10 20 30 40

1,000

2,000

3,000

4,000

5,000

30 minutes intervals

generation (kWh)

(a) The solution of the high level MUCP.

10 20 30 40

1,000

2,000

3,000

4,000

5,000

30 minutes intervals

generation (kWh)

(b) The solution of the high level MUCP, including a de-

tailed ﬂeet planning.

Figure 8: The second use case in more detail.

there would not be sufﬁcient spinning reserve left in

the committed power plants. For this reason, power

plants 1 and 3 have to be committed during these pe-

riods. Secondly, we see many different generators

committed in the ﬁnal planning, in comparison with

the rough planning. However, as we have stated be-

fore, below certain production levels (625 kWh for the

large power plants and 312.5 kWh for the small power

plants) the cost functions are equal, and power plants

are mutually exchangeable. This could explain the

larger number of committed generators. Finally, we

10 20 30 40

500

1,000

1,500

30 minutes intervals

total generation (kWh)

rough planning ﬁnal found solution

Figure 9: Comparison of rough planning and ﬁnal found so-

lution for the planning of the local generators in the second

use case.

show the rough ﬂeet planning and the ﬁnal ﬂeet plan-

ning in one overview in Figure 9. This ﬁgure shows

that the rough planning is matched reasonably well.

6.1 Summary

This paper presents a Multilevel Unit Commitment

Problem (MUCP) for the infrastructure of a smart

grid. This MUCP differs from the common Unit

Commitment Problem (UCP) in its size, the differ-

ence in production levels of the different generator

types, the possibility of demand side load manage-

ment and storage. Objectives may also differ due to

developments in the electricity markets, which leads

to a partial focus shift from the optimization of the

operational costs of generators to the optimization of

the behaviour on the electricity market. In this paper

a use case is deﬁned where a group of 5000 houses

is added to a normal UCP instance, which is planned

MULTILEVEL UNIT COMMITMENT IN SMART GRIDS

369

using the proposed planning method. The results of

the given scenario show that the presented approach

can be applied to a ﬂeet size of 5000 houses.

6.2 Recommendations

In future work scalability should be validated; is it

possible to solve an extended scenario, where multi-

ple ﬂeets are optimized simultaneously? Regarding

this extended scenario, the ﬂeet sizes should be ana-

lyzed for their contribution to the high level optimiza-

tion problem and the speed and quality of the under-

lying lower level optimization problem(s). In this ex-

tended scenario, the inﬂuence of the production ca-

pacity of low level generators on the capability to ad-

just the total output as a ﬂeet also has to be studied.

Also demand side load management should be

added, as well as other local generation or storage

technologies, such as solar cells and heat pumps, to

solve an extended real life Multilevel Unit Commit-

ment Problem. Other types of local generation, de-

mand side load management and local storage can

be incorporated in a similar way as is done for the

microCHP. However, these possibilities cannot be

treated as independent ﬂeets. An additional level

needs to be introduced in the MUCP, where the in-

teractions between these possibilities are considered

as a new type of combined patterns.

REFERENCES

Alanne, K. and Saari, A. (2004). Sustainable small-scale

chp technologies for buildings: the basis for multi-

perspective decision-making. Renewable and Sustain-

able Energy Reviews, 8(5):401–431.

Arsie, I., Marano, V., Rizzo, G., and Moran, M. (2009). In-

tegration of wind turbines with compressed air energy

storage. In Proceedings of the Second Global Con-

ference on Power Control and Optimization (PCO),

pages 11–18. Keynote lecture.

Ayompe, L. M., Duffy, A., McCormack, S. J., and Con-

lon, M. (2010). Validated real-time energy models

for small-scale grid-connected pv-systems. Energy,

In Press, Corrected Proof.

Bakker, V., Bosman, M. G. C., Molderink, A., Hurink, J. L.,

and Smit, G. J. M. (2010). Improved heat demand

prediction of individual households. In Proceedings

of the ﬁrst Conference on Control Methodologies and

Technology for Energy Efﬁciency, Vilamoura, Portu-

gal, pages 1–6, Oxford. Elsevier Ltd.

Bosman, M. G. C., Bakker, V., Molderink, A., Hurink, J. L.,

and Smit, G. J. M. (2010). On the microchp schedul-

ing problem. In Proceedings of the Third Global Con-

ference on Power Control and Optimization (PCO),

pages 367–374.

Bosman, M. G. C., Bakker, V., Molderink, A., Hurink, J. L.,

and Smit, G. J. M. (2011). Controlling a group of

microchps: planning and realization. In Proceedings

of the First International Conference on Smart Grids,

Green Communications and IT Energy-aware Tech-

nologies (ENERGY 2011), pages 1–6.

Groewe-Kuska, N. and Roemisch, W. (2005). Stochastic

Unit Commitment in Hydrothermal Power Production

Planning. Society for Industrial and Applied Mathe-

matics, Philadephia, PA.

Kerr, R., Scheidt, J., Fontanna, A., and Wiley, J. (1966).

Unit commitment. Power Apparatus and Systems,

IEEE Transactions on, PAS-85(5):417 –421.

Lanzafame, R. and Messina, M. (2010). Power curve con-

trol in micro wind turbine design. Energy, 35(2):556–

561. ECOS 2008, 21st International Conference, on

Efﬁciency, Cost, Optimization, Simulation and Envi-

ronmental Impact of Energy Systems.

Molderink, A. (2011). On the three-step control method-

ology for Smart Grids. PhD thesis, University of

Twente.

Padhy, N. (2004). Unit commitment-a bibliographical

survey. Power Systems, IEEE Transactions on,

19(2):1196 – 1205.

Sheble, G. and Fahd, G. (1994). Unit commitment litera-

ture synopsis. Power Systems, IEEE Transactions on,

9(1):128 –135.

United States Department of Energy (2003). The micro-

CHP technologies roadmap. Results of the Micro-

CHP Technologies Roadmap Workshop.

Wemhoff, A. and Frank, M. (2010). Predictions of energy

savings in hvac systems by lumped models. Energy

and Buildings, 42(10):1807 – 1814.

ICORES 2012 - 1st International Conference on Operations Research and Enterprise Systems

370