A QUOTA-BASED MULTI-AGENT NEGOTIATION PROTOCOL FOR
COMPLEX CONTRACTS
Fabian Lang and Andreas Fink
Institute of Computer Science, Helmut Schmidt University Hamburg, Holstenhofweg 85, 22043 Hamburg, Germany
Keywords:
Multi-Agent Systems, Negotiation Protocol, Software Agents, Cooperation, Group Decision Making.
Abstract:
Automated negotiation is regarded as an essential method for the coordination of software agents. However,
without adequate protocols, negotiations are susceptible to malicious and strategic behavior of the agents –
especially when interdependencies of contract items lead to complex contract spaces. In this study, we propose
a mediator-based protocol employing acceptance quotas to ensure cooperative behavior in inter-organizational
systems. Furthermore, we evaluate three potential extensions to the basic protocol. We have conducted sim-
ulation experiments for evaluation which show that the proposed protocol can ensure an effective welfare
performance and that the proposed extensions can result in a further improvement of the basic protocol.
1 INTRODUCTION
Various modern software systems draw on au-
tonomous agents. In software engineering, there are
two considerable hypotheses: firstly, that multi-agent
systems (MAS) provide better opportunities to design
complex, distributed software systems (adequacy hy-
pothesis) and, secondly, that the agent-oriented ap-
proach will succeed as an reliable way of system engi-
neering (establishment hypothesis) (Jennings, 2000).
Agents within multi-agent systems are heteroge-
neous and autonomous (Rosenschein and Zlotkin,
1994). Accordingly, they have to be endowed with
a utility function (Kraus, 1997) – commonly provided
by a human principal. A central task of the design
of a MAS is the coordination of the heterogeneous
agents. Automated negotiation is regarded as the pre-
sumably most suited method for this task (Jennings
et al., 2001). Hence, the coordination is regulated by
a negotiation protocol providing a heuristic body of
rules. To analyze the agents’ interactions, methods
from behavioral science, which centers around hu-
man cooperation and coordination, are found to be ap-
propriate. Nevertheless, such informal environments
need to be evaluated as well, which can be mastered
effectively by conducting simulations (Kraus, 1997).
Regularly, negotiation researchers consider lin-
ear utility functions with well-behaved characteristics
such as monotonicity leading to a single optimum for
each agent (Klein et al., 2003). However, real-world
application can be non-linear as well. For instance,
set-up costs of a machine processing different prod-
ucts or complementary and substitute goods within e-
markets lead to interdependencies which can result in
non-linear, complex contracts with several local op-
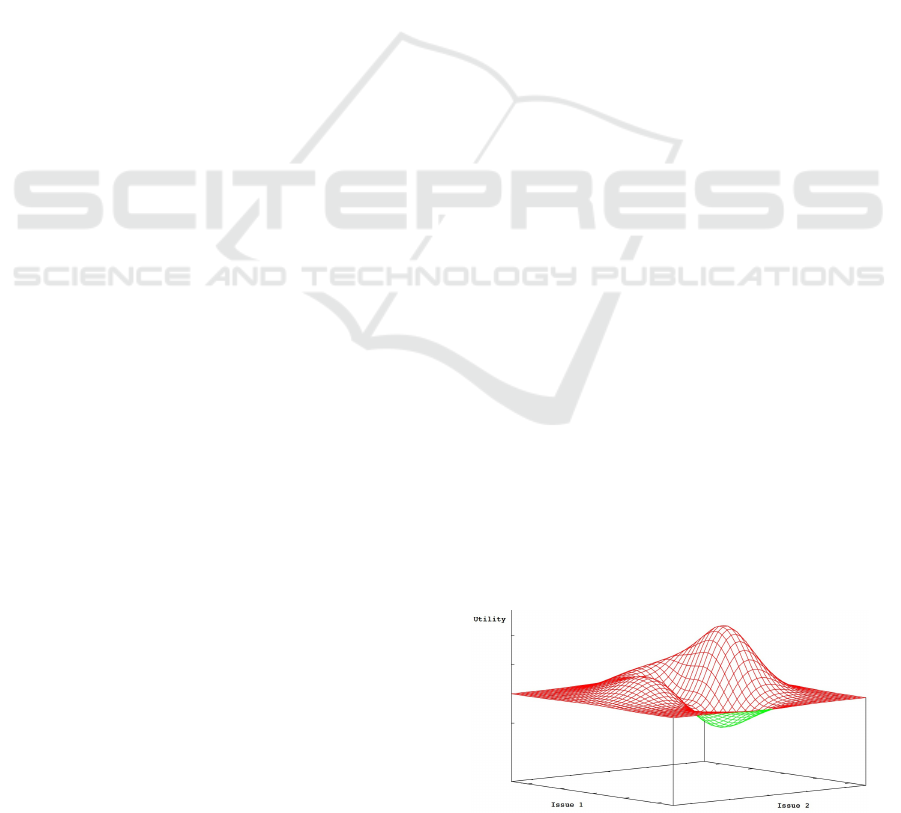
tima (Klein et al., 2003). Figure 1 illustrates a utility
space of a single agent for two interdependent issues.
As shown in the figure, the agent might have to agree
to a deterioration to leave a local utility maximum in
order to achieve a better outcome. However, this pro-
cess might be risky because it is unclear whether the
other agents support the transition and whether they
already have reached their own individual optimum.
Figure 1: Non-linear utility space for two issues.
In the following, we will give a brief overview on
related work and present our formal scenario. Sub-
sequently, we will introduce the proposed negotiation
protocol and its extension and discuss the results of
the simulation experiments. Finally, we will conclude
the study and give an outlook to further research.
113
Lang F. and Fink A..
A QUOTA-BASED MULTI-AGENT NEGOTIATION PROTOCOL FOR COMPLEX CONTRACTS.
DOI: 10.5220/0003717501130118
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 113-118
ISBN: 978-989-8425-96-6
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK
Negotiations have been analyzed by several research
disciplines such as economics, mathematics, sociol-
ogy, psychology, or political science (Conitzer, 2010).
Whereas most work in the field of psychology and so-
ciology is focused on human behavior such as biases,
game theory – mainly adopted by mathematicians and
economists – analyzes rational decisions in negotia-
tion. Best known is probably the Nash bargaining
solution (Nash, 1950). (Rubinstein, 1982) extended
the basic game by introducing strategic interaction of
players (the Rubinstein bargaining model). At this,
the players make proposals in turn and utility de-
creases over time with each round. The model has es-
tablished the strategic (or dynamic) game-theoretical
approach to negotiation. However, these rather the-
oretic approaches can hardly be transfered to auto-
mated negotiation models; real-world problems are
often characterized by highly strategic interactions
and by encapsulated information instead of complete
information (Lai et al., 2006). Negotiations in the
context of software agents gained a lot of interest of
AI researchers. To name a few notable introductory
articles: (Jennings et al., 2001) discuss expectations,
methods, and challenges of automated negotiation re-
search whereas (Kraus, 1997; Kraus, 2001) presents
common methodological approaches and techniques
for multi-agent cooperation. (Conitzer, 2010) sum-
marizes the state of the art focusing on group decision
making of autonomous agents.
Special features of our scenario are a negotiation
space that is complex due to non-linearity of utility
functions as well as a binary coded contract. Sev-
eral papers draw on similar scenarios: (Klein et al.,
2003) propose a simulated-annealing negotiation pro-
tocol providing the idea of annealing agents and us-
ing the same scenario. The interdependencies and the
existence of a mediator are central elements in the
work of (Fujita et al., 2010) and (Hattori et al., 2007).
(Fink, 2006) presents the idea of quotas to force an-
nealing behavior but uses a different cooling sched-
ule procedure. This protocol was applied to the coor-
dination of decentralized multi-project scheduling by
(Homberger, 2009). Finally, we want to refer to (Lai
et al., 2004) who provide a more complete literature
review.
3 SCENARIO
In the scenario, j ∈ {N|0 ≤ j < J} agents participate
in the negotiation. They have to reach a settlement
on a contract c = {d
0
,...,d
i
,...,d
I−1
} incorporating
i ∈ {N|0 ≤ i < I} different contract items. The set
of all possible contracts is called the contract space
C 3 c. The contract item decision d
i
about an item i
can take binary values, thus d
i
∈ {0,1}. The utilities
of the items are mutually interdependent, so that the
agents’ preferences are determined by pairs of items.
Consequently, the preference P
j
(i,
˜
i) is given by a tri-
angular matrix where the diagonal indicates the utility
values for single items. The utility function of a con-
tract c for an agent j, which can be interpreted as a
vector of decisions, is represented as follows:
U
j
(c) =
I−1
∑
i=0
I−1
∑
˜
i=i
P
j
(i,
˜
i) ∗ d(i) ∗ d(
˜
i) (1)
As indicated in (1), the preference for a pair of items
{i,
˜
i} is just relevant if both contract items are ac-
cepted, i.e., d
i
= d
˜
i
= 1. If an item is rejected (d
i
= 0),
the item as well as combinations including this item
have no impact on the utility function. Since cardinal
utilities are supposed, we have chosen the maximiza-
tion of the social welfare (SW) as objective:
SW (c) =
J−1
∑
j=0
U
j
(c) (2)
Furthermore, we assume that no agent would accept a
final contract without any benefit (individual rational-
ity constraint; (Conitzer and Sandholm, 2004)). Thus,
the agents can opt out and leave the negotiation with a
utility of zero. For better comparison, we deploy the
SW optimum to normalize the problem instances. On
this, we have to solve a mixed-integer program de-
picted in (3) where o
j
is a binary variable indicating
whether an agent j opts out (o
j
= 1 ⇒ U
j
(c) ← 0) or
not (o
j
= 0). The SW optimum can just be computed
by supposing full knowledge about the preferences of
the agents. This information is not available for the
agents themselves.
max
d,o
J−1
∑
j=0
I−1
∑
i=0
I−1
∑
˜
i=i
P
j
(i,
˜
i) ∗ d(i) ∗ d(
˜
i) ∗ (1 − o
j
)
s.t. U
j
(c) ∗ (1 − o
j
) ≥ 0 ∀ j ∈ {N|0 ≤ j < J}
d
i
,o
j
∈ {0,1}
(3)
4 NEGOTIATION PROTOCOL
4.1 Overview
In the protocol, a mediator proposes contract candi-
dates and agents choose between a new candidate and
an active contract which is the last accepted contract
candidate by all agents. The basic protocol is shown
ICAART 2012 - International Conference on Agents and Artificial Intelligence
114

Algorithm 1: The basic protocol.
procedure MEDIATED NEGOTIATION PROTOCOL
c
∗
0
← GenerateInitialContract
for t = {0, 1, . . . , τ − 1} do
c
0
t
← Mutate(c
∗
t
)
for all j ∈ {N|0 ≤ j < J} do
Z
j
← AcceptOrRe ject(c
0
t
,c
∗
t
, j)
end for
if
J−1
∑
j=0
Z
j
= J then c
∗
t+1
← c
0
t
else c
∗
t+1
← c
∗
t
end if
end for
c ← c
∗
τ−1
end procedure
as pseudo code in algorithm 1.
Since the agents decide between two contracts, we
need an initial contract c
∗
0
for the first round t = 0. At
first, the mediator randomly generates an initial con-
tract and then randomly mutates a single (or several)
contract item(s) resulting in the contract candidate c
0
t
.
The contract is a binary vector; thus, mutating means
that a decision d
i
on a randomly picked item i be-
comes d
i
← 0, if the decision was d
i
= 1, and vice
versa. After having an active contract c
∗
t
and a con-
tract candidate c
0
t
, the agents decide upon two alterna-
tives resulting in Z
j
. If all agents accept the contract
candidate, i.e., they prefer the candidate to the active
contract, the candidate becomes the new active con-
tract (c
∗
t+1
← c
0
t
); otherwise, the former active candi-
date remains in the next round (c
∗
t+1
← c
∗
t
). In the next
round, the process starts over and the active contract
is mutated again. The process is repeated for τ itera-
tions and the final active – and hence accepted by all
– contract becomes the terminal contract c ← c
∗
τ−1
.
Agent behavior is a very important issue for sys-
tem designers (Binmore and Vulkan, 1999). One aris-
ing question is: How would the agent behave? Game
theory suggests that rational agents seek to maximize
their individual benefit – and not the benefit of the
group. (Klein et al., 2003) present the greedy agent
type who acts like the hill climbing heuristic and
just agrees to contract candidates not making him-
or herself worse off. Consequently, the greedy Hill-
Climber’s (HC) decision function is as follows:
Z
j
=
1, U
j
(c
0
t
) ≥ U
j
(c
∗
t
)
0, U
j
(c
0
t
) < U
j
(c
∗
t
)
(4)
Nevertheless, the main objective should be to em-
ploy a mechanism which results in a desired outcome
(Maskin, 2008). Thus, another question arises: How
should the agents behave? Again, (Klein et al., 2003)
made use of a metaheuristic and propose a cooper-
ative agent type. Cooperative means in this context
that an agent is partly willing to accept a worsen-
ing contract if another agent can achieve an improve-
ment. This agent type acts like the simulated anneal-
ing heuristic and agrees to candidates which make
him- or herself better off but partly also slightly worse
off. Like in the case of the metaheuristic, small dete-
riorations are more likely to be accepted than big ones
and an agent’s willingness to accept worse contracts
is declining over time. The cooperative Simulated-
Annealer’s (SA) decision function is given by:
Z
j
=
1,
U
j
(c
0
t
) ≥ U
j
(c
∗
t
) ∨
e
−[U
j
(c
∗
t
)−U
j
(c
0
t
)]/T
t
≥ U(0,1)
0,
U
j
(c
0
t
) < U
j
(c
∗
t
) ∧
e
−[U
j
(c
∗
t
)−U
j
(c
0
t
)]/T
t
< U(0,1)
(5)
As indicated in equation (5), the agents still accept
individually beneficial contracts. In case of a deteri-
oration, the agents decide according to the Metropo-
lis criterion which is subject to the degree of deteri-
oration, a temperature T
t
, and a uniformly distributed
random number (U(0,1)). The temperature decreases
over time and hence the likelihood of accepting a
worse contract declines as well. Finally, if the tem-
perature converges to zero, the cooperative agents be-
have identically like the HC. The differences between
those two types become clear when the two agent
types compete against each other – as shown in the
game in table 1.
Table 1: Bilateral negotiation game: A prisoner’s dilemma.
Greedy Cooperative
Greedy
3135; 3065 5905; 628
(
∑
6200) (
∑
6533)
Cooperative
628; 5905 3736; 3752
(
∑
6533) (
∑
7488)
Whereas the SAs achieve a very good individual
and collective welfare, an agent can make him- or
herself better off significantly by switching to a hill
climbing strategy. However, the opponent agent can
also improve his or her outcome by behaving greedily
in the same way. Finally, in the strategy set in which
both act greedily, a deviation from the strategy can-
not result in a better outcome so that this strategy set
constitutes a Nash equilibrium – the only one in this
game. Consequently, all agents behave greedily and a
good welfare outcome cannot be reached. This game
is an instance of the classical Prisoner’s Dilemma.
Consequently, we need a mechanism forcing the
agents to behave cooperatively like the SA instead of
greedily like the HC. A central and plausible supposi-
tion is that if the agents have to accept more contracts,
A QUOTA-BASED MULTI-AGENT NEGOTIATION PROTOCOL FOR COMPLEX CONTRACTS
115

they will behave like a SA. The SA’s strategy, namely
to accept small and early deteriorations, is reason-
able since small ones are evidently better than bigger
ones, and early ones can be set off in the subsequent
course of the negotiation. Ergo, we introduce manda-
tory acceptance quotas: The mediator specifies and
monitors quotas for various phases of the negotiation
p = {p
1
,..., p
γ
,..., p
Γ
}. These quotas decline with
each phase of the negotiation and converge to zero.
For instance, in the first thousand rounds (γ = 1), the
mediator demands 400 accepted contract candidates
(p
1
= 40%) and in the following thousand rounds
(γ = 2) 390 (p
2
= 39%). In the final thousand iter-
ations (γ = Γ), this threshold will have declined to,
e.g., p
Γ
= 1%. The agents determine their cooling
schedule accordingly and in- or decrease their tem-
perature T
t
subject to the required quota. The imple-
mentation results in a step-shaped cooling schedule.
In the simulations, we adopted a temperature update
algorithm: The agents check their current acceptance
ratio regularly (e.g., every 100 rounds). If they are
below their projected aim, they increase their temper-
ature to accept more contracts in the following sub-
phases. Analogously, they decrease their temperature
when they temporarily have exceeded their intended
aims.
4.2 Extensions
In the following, we will present and evaluate three
ideas to enhance the basic negotiation protocol.
4.2.1 Three-valued Logic
By now, we have assumed that the cooperative agent
decides according to (5) and can return 1 (accept) or 0
(reject). Additionally, we now introduce a third state
(0.5) which enables to express that a contract is ac-
cepted involuntarily due to the quota restriction:
Z
j
=
1, U
j
(c
0
t
) ≥ U
j
(c
∗
t
)
U
j
(c
0
t
) < U
j
(c
∗
t
) ∧
0.5, e
−[U
j
(c
∗
t
)−U
j
(c
0
t
)]/T
t
≥ U(0,1)
U
j
(c
0
t
) < U
j
(c
∗
t
) ∧
0, e
−[U
j
(c
∗
t
)−U
j
(c
0
t
)]/T
t
< U(0,1)
(6)
If all agents return 0.5, i.e., all agents just accept the
proposal due to the quotas, then the mediator rejects
this proposal (Z
j
← 0 ∀ j|Z
j
= 0.5). However, if at
least one agent benefits from the proposal and returns
Z
j
= 1 while the other agents return 0.5, the decisions
being 0.5 become 1 (Z
j
← 1 ∀ j|Z
j
= 0.5). The ob-
jective of this extension is to prevent Pareto-inferior
moves. This additional revelation of information is
arguable because we suppose, along with the litera-
ture, that agents dislike information revelation (Hat-
tori et al., 2007). Nevertheless, the limits of revelation
willingness are hard to determine and surely depend-
ing on the application context so that we have consid-
ered this approach as an option in the simulation.
4.2.2 Agent-based Proposals
In the basic protocol, a mediator proposes contract
candidates representing mutations of the actual active
contract (last all-agreed contract). Since the mediator
randomly picks a new contract item to mutate due to
lacking better information, there is no sophisticated
movement while searching the contract space. There-
fore, we have implemented an agent-based proposal
scheme. In each iteration, another agent proposes the
mutation of the active contract with the greatest im-
provement for him or her. If an item was proposed
and rejected, this item is blacklisted. The black list
is cleared once a proposal is accepted by the group.
Since the agents are forced to propose a contract,
they can be forced to propose a deteriorating contract.
To determine their best contract mutation, the agents
have to evaluate all possible mutations which can be
runtime demanding. This can be circumvented by rul-
ing decision time limits so that the agents would need
smart heuristics for the determination of the best con-
tract. However, we will disregard this runtime issue
and use complete enumeration in the simulation.
4.2.3 Unanimity vs. Majority
So far, the scenario demands an unanimous decision.
Voting methods are a widespread and important tool
for group decision making (Conitzer, 2010). That is
why we extended the scenario by a simple majority
voting. Here, a contract candidate becomes the new
active contract if the majority of all agents accepts
this candidate (
∑
J−1
j
Z
j
> J/2). The agents have the
choice between two contracts or alternatives, respec-
tively. Concerning this, (May, 1952) showed gen-
erally that the simple majority rule is an egalitarian,
neutral, non-manipulable, and resolute voting proce-
dure for two alternatives – given that ties are forbid-
den.
5 PROTOCOL EVALUATION
There is much to suggest that the protocol’s dynam-
ics are too complex to be abstracted in a theoreti-
cal model adequately. Therefore, we have conducted
ICAART 2012 - International Conference on Agents and Artificial Intelligence
116

simulation experiments to evaluate the protocol with
nine different configurations. Based on our scenario,
we have generated 1,000 equally distributed prefer-
ence sets P
j
(i,
˜
i) ∼ U(−100,100) for J = 5 agents
and I = 50 contract items providing 1,000 problem in-
stances. Each negotiation simulation lasted 50,000 it-
erations meaning 50,000 different contract proposals.
In these iterations, the protocol has to search the over-
all contract space consisting of 2
I
= 2
50
≈ 1.13 ∗ 10
15
possible contracts. We have computed the theoreti-
cal welfare optimum (TO) for these test instances by
solving the mixed-integer program from equation (3)
(supposing complete information). Below, we ana-
lyze the protocol’s performance using the welfare as a
percentage of the TO as performance measure. More-
over, we have conducted pair-wise comparisons em-
ploying a Wilcoxon rank-sum test to validate the sta-
tistical significance (p-Value) of the results. In the
subsequent tables, the subscript of the p-Value indi-
cates the comparison data set.
5.1 Basic Protocol
At first, we examine the basic setup of the protocol,
i.e., negotiation with and without acceptance quotas.
The quotas are parameterized such that the agents col-
lectively accept about 40% in the beginning and about
1% in the end of the negotiation. Like mentioned be-
forehand, we assume that without quotas the agents
behave like Hill-Climbers (HC) and with quotas like
Simulated Annealers (SA). Table 2 shows average re-
sults for the 1,000 problem instances.
Table 2: Performances of the two agent types.
HC SA
p-Value – 1.0
HC
Mean 23.6% 89.3%
As we have expected, hill climbing performs un-
satisfying. After the first few hundred iterations, the
negotiation usually gets stuck in the very same active
contract because the greedy agents do no longer ac-
cept any proposal. In contrast, the quota rule fulfills
its objective and results in a convincing social wel-
fare. The agents are forced to continue accepting pro-
posals and therefore an individual agent cannot ob-
struct the group’s progress.
5.2 Extensions
Now, we analyze the results of the presented exten-
sions. We have, for ease of exposition, used abbrevi-
ations to code the protocol’s configuration:
3 – three-valued logic
P – agent proposal
M – majority rule.
5.2.1 Separate Effects
Table 3 shows the results of using only one extension.
Table 3: Performances of the extensions (separate).
SA-3 HC-P SA-P
p-Value 0.96
SA
0.62
HC
1.0
SA
Mean 89.6% 23.4% 92.0%
HC-M SA-M
p-Value 1.0
HC
1.0
SA
Mean 85.3% 56.3%
The adoption of a three-valued logic does not lead
to a substantial increase of social welfare. As argued
beforehand, this extension forces the agents to reveal
information which they presumably do not want to
share. The improvement seems rather small to jus-
tify the additional revelation. When the proposal sub-
mittal is assigned to the agents instead of the medi-
ator, the protocol employing quotas can improve its
performance substantially. In contrast, when greedy
agents are in place, there is neither a considerable
nor a statistically significant shift in the performance
compared to mediator-based proposals. However, the
majority rule yields a considerable improvement for
greedy agents. The detachment of the unanimity cri-
terion results in accepted contracts that are partially
deteriorative for a subset of the agents. This follows
our argumentation of the proposed cooperative agent
type. However, the HC-M outcome (85.3%) is signif-
icantly worse than the results of SA (89.6%) and SA-
P (92.0%). When the majority rule is adopted along
with quotas, the welfare decreases strongly. Presum-
ably, the acceptance of worsening contracts is re-
peated unnecessarily leading to too many acceptions.
5.2.2 Combinatorial Effects
Besides the separate adoption of the extensions, there
are possible combinatorial applications. In the hill
climbing variant, the majority rule and the agent-
based proposal scheme can be combined; in the sim-
ulated annealing variant, there are several feasible
combinations. However, since the majority rule did
not perform well, we have neglected these configu-
rations and just analyzed the combination of three-
valued logic and agent-based proposal. The results of
the combined extensions are shown in table 4.
The results indicate that none of the combinations
can lead to a further improvement of the protocol’s
A QUOTA-BASED MULTI-AGENT NEGOTIATION PROTOCOL FOR COMPLEX CONTRACTS
117

Table 4: Performances of the extensions (combinations).
HC-P-M SA-3-P
p-Values 0.99
HC−P
1.0
SA−3
1.0
HC−M
0.95
SA−P
Mean 85.2% 91.8%
welfare performance. Neither HC-P-M nor SA-3-P
can perform better than HC-M or SA-P, respectively,
but the performances are similar in scale. Once more,
the three-valued logic outcome does not justify the ad-
ditional information revelation.
6 CONCLUSIONS AND
OUTLOOK
In this paper, we present and evaluate a quotas-based
negotiation protocol ensuring cooperation between
autonomous agents. We discuss two different agent
types: the Hill Climber acting greedily and the Sim-
ulated Annealer acting cooperatively due to accep-
tance quotas. Additionally, we propose three exten-
sions and analyze their effect depending on the two
agent types. The findings of the simulation experi-
ments show that the protocol achieves good welfare
outcomes by means of quotas, whereas the protocol
without quotas – and hence with greedy agents – per-
forms very poor supposing unanimity. However, the
straightforward application of a simple majority rule
can lead to rather good results without quotas but de-
teriorates the outcome of the protocol with quotas.
The introduction of a three-valued logic does not im-
prove the outcome significantly. Nevertheless, the
more sophisticated concept of acceptance quotas per-
forms significantly better than without quotas. Fur-
thermore, an agent-based proposal scheme can im-
prove these results in addition.
Future work will keep focusing on negotiation
protocols for complex contracts. By now, we have
analyzed situations with a single contract candidate
which can be enhanced by several candidates leading
to voting settings. A further aspect is runtime as some
mechanisms are more runtime demanding than oth-
ers. Moreover, we will conduct a sensitivity analysis
of more agents, more contract items, and more itera-
tions, and are going to incorporate real-world problem
sets and problem instances in our studies.
REFERENCES
Binmore, K. and Vulkan, N. (1999). Applying game theory
to automated negotiation. Netnomics, 1(1):1–9.
Conitzer, V. (2010). Making decisions based on the pref-
erences of multiple agents. Communications of the
ACM, 53(3):84–94.
Conitzer, V. and Sandholm, T. (2004). Self-interested auto-
mated mechanism design and implications for optimal
combinatorial auctions. Proceedings of the 5th ACM
Conference on Electronic Commerce (EC 04).
Fink, A. (2006). Supply chain coordination by means of
automated negotiations between autonomous agents.
In Chaib-draa, B. and M
¨
uller, J., editors, Multia-
gent based Supply Chain Management (Studies in
Computational Intelligence, Vol. 28), pages 351–372.
Springer, Berlin/Heidelberg, Germany.
Fujita, K., Ito, T., and Klein, M. (2010). Secure and effi-
cient protocols for multiple interdependent issues ne-
gotiation. Journal of Intelligent and Fuzzy Systems,
21(3):175–185.
Hattori, H., Klein, M., and Ito, T. (2007). Using itera-
tive narrowing to enable multi-party negotiations with
multiple interdependent issues. In Proceedings of the
Sixth International Joint Conference on Autonomous
Agents and Multi-Agent Systems (AAMAS 07), pages
1043–1045.
Homberger, J. (2009). A (µ, λ)-coordination mechanism for
agent-based multi-project scheduling. OR Spectrum.
doi: 10.1007/s00291-009-0178-3.
Jennings, N. R. (2000). On agent-based software engineer-
ing. Artificial Intelligence, 117(2):277–296.
Jennings, N. R., Faratin, P., Lomuscio, A. R., Parsons, S.,
Sierra, C., and Wooldridge, M. (2001). Automated ne-
gotiation: Prospects, methods and challenges. Group
Decision and Negotiation, 10(2):199–215.
Klein, M., Faratin, P., Sayama, H., and Bar-Yam, Y. (2003).
Negotiating complex contracts. Group Decision and
Negotiation, 12(2):111–125.
Kraus, S. (1997). Negotiation and cooperation in multi-
agent environments. Artificial Intelligence, 94(1):79–
97.
Kraus, S. (2001). Automated negotiation and decision mak-
ing in multiagent environments. In Luck, M., Marik,
V., Stepankova, O., and Trappl, R., editors, Multi-
agents Systems and Applications, Vol. 104, pages
150–172. Springer, New York, NY, USA.
Lai, G., Li, C., and Sycara, K. (2006). Efficient multi-
attribute negotiation with incomplete information.
Group Decision and Negotiation, 15(5):511–528.
Lai, G., Li, C., Sycara, K., and Giampapa, J. (2004). Litera-
ture review on multi-attribute negotiations. Technical
Report, CMU-RI-TR-04-66. Carnegie Mellon Univer-
sity, Pittsburgh, PA, USA.
Maskin, E. S. (2008). Mechanism design: how to im-
plement social goals. American Economic Review,
98(3):567–576.
May, K. (1952). A set of independent necessary and suffi-
cient conditions for simple majority decision. Econo-
metrica, 20(4):680–684.
Nash, J. F. (1950). The bargaining problem. Econometrica,
18(2):155–162.
Rosenschein, J. S. and Zlotkin, G. (1994). Designing con-
ventions for automated negotiation. AI Magazine,
15(3):29–46.
Rubinstein, A. (1982). Perfect equilibrium in a bargaining
model. Econometrica, 50(1):97–110.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
118
