
TOWARDS COGNITIVE STEERING BEHAVIOURS FOR
TWO-WHEELED ROBOTS
Franc¸ois Gaillard
1,2
, C´edric Dinont
1
, Micha¨el Soulignac
1
and Philippe Mathieu
2
1
ISEN Lille, CS Dept., 41, Boulevard Vauban, 59046 Lille Cedex, France
2
LIFL, University of Lille 1, UMR USTL/CNRS 8022, 59655 Villeneuve d’Ascq Cedex, France
Keywords:
Robot and multi-robot systems, Cognitive robotics, Task planning and execution, Steering behaviours.
Abstract:
We present a two-layer architecture for two-wheeled robots trajectory planning. This architecture can be used
to describe steering behaviours and to generate candidate trajectories that will be evaluated by a higher-level
layer before choosing which one will be followed. The higher layer uses a TÆMS tree to describe the current
robot goal and its decomposition into alternative steering behaviours. The lower layer uses the DKP trajectory
planner to grow a tree of spline trajectories that respect the kinematic constraints of the problem, such as
linear/angular speed limits or obstacle avoidance. The two layers closely interact, allowing the two trees to
grow simultaneously: the TÆMS tree nodes contain steering parameters used by DKP to generate its branches,
and points reached in DKP tree nodes are used to trigger events that generate new subtrees in the TÆMS tree.
We give two illustrative examples: (1) generation and evaluation of trajectories on a Voronoi-based roadmap
and (2) overtaking behaviour in a road-like environment.
1 INTRODUCTION
Our aim is to provide human-like steering behaviours
to autonomous mobile robots with the respect of their
physical constraints. We would like to design robotic
applications using high-level building blocks repre-
senting motion strategies like follow or overtake and
behaviours like drive smoothly or drive aggressively.
This kind of problem has already been addressed
for autonomous simulated characters by (Reynolds,
1999) who proposed a two-layer architecture to ex-
press steering behaviours.
We reuse here the basic idea from Reynolds but
transposing on real-world robots results that work
for simulating characters raises some problems. The
main one lies in the link between the cognitive layer
of the robot and the trajectory planning layer. An
action selection level first decides which high-level
goals are given to the motion planning layer. Such
an approach hides the motion planning and locomo-
tion problems, so the completeness and kinodynamic
constraints respect issues exist. The action selection
level cannot verify the trajectory feasibility of the de-
cisions and it appears difficult to encode the kinody-
namic constraints within this level.
In the context of robotic arms, some recent ad-
vances have been done in mixing planning, using
PDDL for instance (McDermott et al., 1998), and mo-
tion planning when the configuration space can be en-
tirely precomputed (Jaesik and Eyal, 2009) but they
still do not consider kinematic constraints. Eventu-
ally, some recent works mix sample-based approaches
in both discrete and continuous hybrid state spaces
(Branicky et al., 2006) but the configuration space
may grow exponentially (Jaesik and Eyal, 2009). Re-
alism of driving behaviours also becomes an impor-
tant challenge in traffic simulations. Like in our case,
the main difficulty lies in the link between high (psy-
chological) and low (measurable) levels. This prob-
lem has for instance been addressed in (Lacroix et al.,
2007) using probabilistic distributions of some mea-
surable parameters like time to collision or time to line
crossing to generate the variety of behaviours encoun-
tered in the real world.
Our solution uses two different closely interacting
layers. Each layer grows a tree which construction
influences the building of the other: the trajectory tree
and the steering tree.
The trajectory tree contains trajectory samples
dynamically extended using the steering parameters
from the steering behaviours expressed in the steer-
ing tree. We use our sample-based approach named
DKP, first presented in (Gaillard et al., 2010) and suc-
cessfully applied on real robots (Gaillard et al., 2011).
119
Gaillard F., Dinont C., Soulignac M. and Mathieu P..
TOWARDS COGNITIVE STEERING BEHAVIOURS FOR TWO-WHEELED ROBOTS.
DOI: 10.5220/0003717701190125
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 119-125
ISBN: 978-989-8425-96-6
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: Example of DKP quadratics samples tree in
magenta. The final trajectory from Start to Goal is in blue.
With its selection/propagation architecture, DKP pro-
vides properties for the low layer that we need to build
a cognitive trajectory planner. It produces trajectories
that respect the kinematic constraints of the robot and
avoid obstacles as shown in Figure 1. It also translates
steering behavioursinto parameters for the underlying
trajectory planner. Finally, it provides solutions that
optimize a criterion and it is deterministic: the cogni-
tive part should not have to repeat trajectory planning
until an optimal solution is found if one exists.
The steering tree is made up of instantiated
models of HTN (Hierarchical Task Networks) sub-
trees representing steering behaviours. Common ap-
proaches are based either on a STRIPS-like descrip-
tion of the world and possible actions, or on HTN
decomposition of goals into compound tasks. HTN
have been widely used because they allow a human-
friendly description of tasks, even if their practical ex-
pressiveness is not better than STRIPS (Lekavy and
N´avrat, 2007). We use TÆMS (Decker, 1996), which
is a formalism used to describe HTN, to describe
complex tasks using resources, having durations and
complex interrelations, which is the case in robotic
applications.
So, our approach combines top-down and bottom-
up interactions. The latter provides a way for the bot-
tom layer, DKP, to give information to a cognitive top
layer, using TÆMS, allowing it to decide which ac-
tion to take based on different evaluable alternatives.
The paper is organized as follows. Section 2 details
our two-layer architecture. Sections 3 and 4 give two
examples demonstrating the benefits of our architec-
ture for roadmap-based guidance and for the evalua-
tion of various steering behaviours in an overtaking
scenario.
2 STEERING BEHAVIOURS FOR
TRAJECTORY PLANNING
We propose to create a steering behaviour driven tra-
jectory planner. Two trees grow in parallel: a steer-
ing behaviour tree and a trajectory tree, following the
model in (Reynolds, 1999). The steering behaviour
tree controls the trajectory tree growth and DKP in-
ternal selection/propagation properties, following the
trajectory tree state. The trajectory tree created by
DKP grows if possible in the environment and trig-
gers the instantiation of new behaviours in the steer-
ing behaviour tree in reaction to situations encoun-
tered in the environment. The steering behaviour tree
reflects the trajectory tree: each steering behaviour
corresponds to a valid subtree of the DKP trajectory
tree if this steering behaviourrespects the dynamics of
the robot. Finally, this steering behaviour tree is used
to select the chain of behaviours to follow using the
TÆMS formalism. Our architecture can be seen as a
roadmap based planner where waypoints are replaced
by steering behaviours situated in the environment.
2.1 Controlling DKP with Steering
Parameters
In DKP, all trajectory planning constraints c such
as kinematic constraints and obstacles avoidance con-
straints require a geometrical representation S
c,tr
c
(t),
moved along tr
c
(t) for mobile obstacles. DKP also
needs the transformations T
c
from the constraint basis
to the parameter space basis and back. Finally, a con-
straint c is the tuple (S
c,p
(t),T
c
). Let C = {c
k
} denote
the set of constraints applied to a sample.
We define a goal guidance for propagation level
by the tuple (A
Goal,tr
Goal
(t),Goal) which associates a
Goal state to a delimited zone of the environment
A
Goal,tr
Goal
(t), represented with constructive surface
geometry approach, moved along tr
Goal
(t). The prop-
agation part of DKP extends an exploration tree in the
environment. When the end point of a selected sam-
ple p
k
0
...k
n
(t) is contained in A
Goal,tr
Goal
(t), the next
grown samples minimize the distance to the associ-
ated Goal in the propagation level. A set of propa-
gation goal guidances is denoted PGuide and A
PGuide
is the set of areas which are associated to a goal
within a set of goal guidances. We require that the
areas from A
PGuide
do not overlap: A
Goal,tr
Goal
,k
(t) ∩
A
Goal,tr
Goal
,l
(t) =
/
0 with k 6= l.
With the same formalism than propagation goal
guidance, we define goal guidance for selection level
with a set denoted SGuide. These goals work sepa-
rately from the propagation level to guide the explo-
ration tree created by the selection level. Only one
goal may be defined to keep the good properties from
the selection process (which works in an A
∗
manner).
Time properties in propagation level are T
min
,
the minimal sample duration; T
max
, the maximal
sample duration and Sample
step
, the time interval
ICAART 2012 - International Conference on Agents and Artificial Intelligence
120

in order to produce samples of duration T
min
,T
min
+
Sample
step
,...,T
max
. A discretisation step step is set
for evaluating constraints in the propagationlevel. So,
the tuple T
pr
= (T
min
,T
max
,Sample
step
,step) describes
the inherited time properties of the samples in the
exploration tree. In the backtracking mode used for
this paper, only one sample is created for each prop-
agation step: Sample
step
= 0 and T
min
= T
max
. The
time discretisation for constraints evaluation is set to
step = T
max
/10.
An area parameters set sp is the tuple
(A
sp,tr
c
(t),C
sp
,PGuide
sp
,SGuide
sp
,T
prop
) associating
to an area A
sp,tr
c
of the workspace W some steering
parameters: a set of constraints C
sp
, a set of goal
guidance for the propagation level PGuide
sp
, a set of
goal guidance for the selection level SGuide
sp
and the
time properties T
pr
. The steering parameters set, de-
noted SP, contains all the area parameters sets. Let
A
SP
be the set of areas that are associated to steering
parameters.
2.2 Simultaneously Growing Trees
The complete steering behaviour tree is built using
automatic instantiation of subtree models represent-
ing the steering behaviour library of the application.
We use the TÆMS formalism (Horling et al., 1999).
Even if our architecture does not limit the usage of
any of the TÆMS quality accumulation functions, in
this paper, we only use two of them:
• q seq sum used when all the subtasks need to be
completed in order before giving a quality to the
supertask. In this case, the supertask will get the
combined quality of all its subtasks as its quality;
• q max, which is functionally equivalent to an OR
operator. It says that the quality of the supertask
is equal to the maximum quality of any one of its
subtasks.
We propose an area triggering system to apply
steering behaviours on the exploration tree: each node
in the TÆMS tree contains a steering parameter set
SP associated to an area set A
SP
. When the end-
ing point of a selected sample p
k
0
...k
n
(t) in the DKP
tree is contained in A
sp
k
,tr
c
,k
(t), this sample is prop-
agated using the steering parameters from sp
k
, over-
riding the previous area parameters set sp
k−1
which
ruled the guidance of the exploration tree until this
sample. It means that other samples not concerned
by this triggering will pursue using their respective
steering parameters. When applied, the next samples
in the exploration tree also inherit sp
k
until new steer-
ing parameters are applied on one of the next samples
and so on. When only one area from A
SP
can be trig-
gered as a successor of an area parameters set sp
0,...,k
,
we create a q seq sum node in the TÆMS tree with
two children: the first one contains the area parame-
ters set sp
0,...,k
and the second one contains the next
area parameters set sp
0,...,k,k+1
. If an area parame-
ters set sp
0,...,k,k+1,k+2
can be triggered as a successor
of the area parameters set sp
0,...,k,k+1
, sp
0,...,k,k+1,k+2
is added to the q seq sum node. When n areas from
A
SP
can be triggered as successors of an area parame-
ters set sp
0,...,k
, we create a q max node in the TÆMS
tree with n children containing the associated area pa-
rameters sets. This q max node is added as a child
to the q seq sum node containing sp
0,...,k
. When the
end point of a selected sample p
k
0
...k
n
is contained in
A
sp,p
(t), the next grown samples of the exploration
tree are created respecting the corresponding set of
constraints C
sp,k
and using the corresponding set of
goal guidance for the propagation level PGuide
sp,k
,
goal guidance for the selection level SGuide
sp,k
and
the time properties of the exploration tree.
The DKP exploration tree interacts closely with
the steering behaviour tree thanks to the area trigger-
ing system. When the end point of a selected sample
p
k
0
...k
n
is contained in n areas A
sp,tr
c
(t), we create n
independent new forks in the DKP tree. We can see
each fork as a new DKP exploration subtree with the
sample p
k
0
...k
n
as root, each first sample child apply-
ing one of the n steering parameter sets. Nevertheless,
some samples may overlay in the workspace, espe-
cially those near the root sample p
k
0
...k
n
from which
the n different steering parameters sets are expanded.
3 ILLUSTRATIVE EXAMPLES:
ROADMAP-BASED GUIDANCE
We use the environment of Figure 1 for this first ex-
ample which illustrates the use of the steering tree to
guide the trajectory planning algorithm on a roadmap.
A roadmap captures the connectivity of the different
areas of the environment. It is made up of precom-
puted paths allowing the mobile robot to explore the
environment while avoiding obstacles.
Among the numerous existing approaches pro-
posed in literature, we opted for a Voronoi diagram
because it has the property of keeping the robot away
from obstacles: the paths composing the roadmap
are equidistant to obstacles boundaries. This obstacle
clearance property naturally provides a good roadmap
to guide the robot. It also let it substantially deviate
from it because the area around the roadmap is free.
An example of roadmap generated with a Voronoi
diagram is provided in Figure 3(a) (thick light grey
lines). This is done in two steps. First, the contours of
obstacles and of the environment bounds are discre-
TOWARDS COGNITIVE STEERING BEHAVIOURS FOR TWO-WHEELED ROBOTS
121
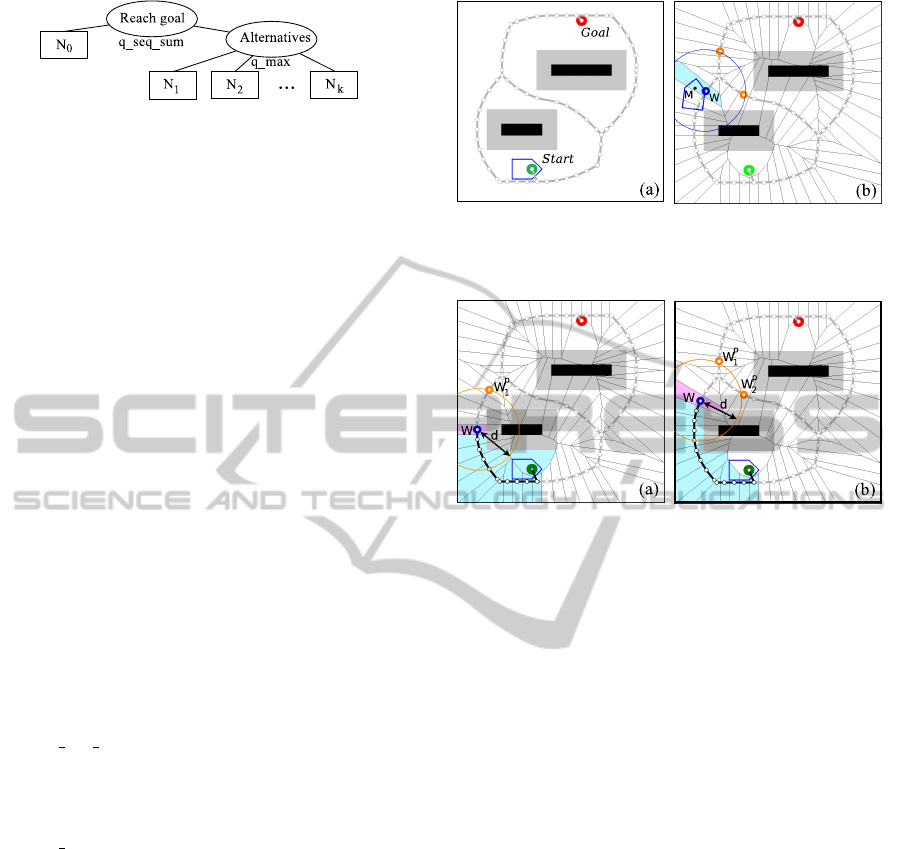
Figure 2: The TÆMS crossroads pattern to be instantiated
in the steering tree.
tised to obtain a set of points from which we generate
a Voronoi diagram. Second, the Voronoi diagram is
simplified by removing the segments crossing obsta-
cles or going to the boundary of the environment.
To perform the guidance of the robot over the
roadmap, we have to retrieve the nearest waypoint
W in the roadmap to any potential location M of the
robot in the environment. This can be efficiently done
by building a meta Voronoi diagram: a Voronoi di-
agram around the Voronoi diagram waypoints. We
obtain a polygonal decomposition of the environment
illustrated in Figure 3(b) (thin black lines). Each poly-
gon P contains a unique waypoint W of the roadmap.
The area of P contains all the points of the environ-
ment closer to W than the other waypoints. We see
in Figure 3(b) that from a robot location M, we can
retrieve the containing polygon P (filled in magenta)
and then the associated waypoint W (plotted in blue).
Using this cellular decomposition, we can build
the steering tree making the bridge between the tra-
jectory planner and the roadmap. The steering tree
models all the possible strategies to bypass the obsta-
cles. A bypassing strategy can be modelled by the
TÆMS crossroads pattern illustrated in Figure 2:
• the q seq sum node expresses the trajectory has
not reached the goal and has to be continued. The
N
0
node corresponds to the part which has already
been done and for which we have an evaluation.
• the q max node chooses the best alternative (i.e.
the alternative of maximal quality) between the
steering behaviour subtrees N
1
, ..., N
k
, that is, the
best bypassing strategy among k.
The steering tree is made up of instantiated cross-
roads patterns. It is progressivelybuilt thanks a depth-
first traversal of the roadmap, from the Start way-
point. Each time a waypoint W of the roadmap is
visited, it is projected at a given distance d on the
roadmap. This projection consists in finding on the
roadmap the k waypoints W
p
i
, (i ∈ {1, k}) situated at
least at the distance d from W. This is depicted in
Figure 4 where projected waypoints are plotted in or-
ange. Note that if the projected waypoint has already
been visited, it is ignored.
This notably forbids to go backward and perform
loops. This can be observed in Figure 4, where vis-
ited waypoints are illustrated through their associated
Figure 3: (a) A roadmap as a simplified Voronoi diagram
(thick grey lines). (b) Meta Voronoi diagram (thin black
lines) associating a unique area to each roadmap waypoint.
Figure 4: Roadmap waypoint W associated to a robot posi-
tion M, and projected waypoints W
p
i
at a distance d. (a) 1
projected waypoint, on 1 branch, before the crossing, (b) 2
projected waypoints, on 2 branches, after crossing.
area, depicted in cyan. For instance, for the W way-
point from Figure 4(a), there would be two theoretical
projected waypoints: W
p
1
(above W) and W
p
2
(below
W), but W
p
2
is not considered.
When creating steering parameter set SP
N
i
associ-
ated to steering node N
i
, two cases are possible. First,
if the projection process leads to a unique projection
waypoint (k = 1), the pair (P,W
p
1
) is added to the set
of goal guidance for the propagation level PGuide
sp,k
.
Second, when several projected waypoints are de-
tected (k > 1), a crossing in the roadmap has been
passed and the considered polygons P are identified
as triggering areas A
sp,k
for each k new steering pa-
rameters set SP
N
i+k
. In this case, a new crossroads
pattern is instantiated in the steering tree, associating
the new steering parameter sets to TÆMS nodes and
generating new alternatives to be evaluated.
Figure 5 shows the steering tree associated to the
environment of Figure 4. This steering tree allows
the trajectory tree of Figure 6 to evaluate the 4 pos-
sible steering behaviours, by planning the 4 associ-
ated trajectories (drawn in blue). The distance d used
to project waypoints on the roadmap directly impacts
the smoothness of the trajectories, allowing smooth
turns in places where the roadmap has sharp corners.
Generated trajectories are guaranteed to be feasible by
the robot and contain its required speed for all points,
ICAART 2012 - International Conference on Agents and Artificial Intelligence
122

which is not the case of the initial Voronoi based
roadmap. Once all the alternatives are known, the
best one can be chosen, according to an application-
dependent criterion (e.g. curvature, length, time or
energy spent).
If we compare the DKP tree of Figure 1 to the one
of Figure 6, we can see that the shape of the final tra-
jectories are better than when DKP runs alone. The
tree also contains much lesser branches, resulting in
faster computation, even with better environment ex-
ploration.
4 ILLUSTRATIVE EXAMPLES:
OVERTAKING
Description. For this example, we consider the fol-
lowing scenario, illustrated by Figure 9. A fast robot
R
0
moves as fast as possible on a road-like environ-
ment with two lanes. Robot R
0
starts moving at the
beginning of the bottom lane and wants to go to the
extremity of this lane. A slower robot R
1
also moves
straight on the bottom lane at a constant speed S
1
. In
the top lane, another robot R
2
also moves at a con-
stant speed S
2
= S
1
, in the opposite direction. The
road is 500m long and 6m wide. Robot dimensions
are 4m×1.7m (like a small car). The clearance on the
robot sides is set to 1.15m. Robots R
1
and R
2
move
at a speed of 110 km/h (∼ 30m/s) on their respective
lanes. R
0
must reach an overall goal G
1
(t) set at the
end of the bottom lane (main goal set in SGuide).
As shown in (Gaillard et al., 2011), DKP can deal
with this kind of overtaking situation. From our point
of view, the solution (the one from DKP used alone
or solutions from other hybrid trajectory planners) is
a ”forward obstacle avoidance”: there is no reason-
ing or adaptation about the kinematic constraints or
the samples duration during the trajectory planning
(except for the backtracking process). The kinematic
constraints are too low to apply to a common overtak-
ing situation that we may meet on our roads. More-
over, even if the kinematic constraints may allow an
overtake, if the robot R
2
starts too close, DKP may
fail to provide an intuitive ”wait and follow” solution:
in DKP, the trajectory is forced to move as far as pos-
sible because of the distance minimizing criterion.
Using steering behaviours, we can deal with this
situation with more realistic parameters. This al-
lows to get and evaluate both follow and overtake be-
haviours. We first set the initial following steering be-
haviour for the robot R
0
. To reach the Goal G
1
(t), R
0
cruises fast at a maximum speed of 130 km/h: the lin-
ear speed constraint is set to [30,36]m/s, time samples
are set to 0.5s and G
1
(t) is added to SGuide.
When R
0
catches up with R
1
, i.e. enters in area
A
1
(t) behind R
1
, it triggers the instantiation of the fol-
low or overtake steering behaviour. Two alternatives
are set under a q max node and are added to the steer-
ing tree. R
0
may adjust its speed to R
1
one and fol-
low it: the linear speed constraint is set to [27,30]m/s,
time samples are set to 1s (following a robot cruising
at a constant speed does not require very reactive ma-
noeuvres) and G
1
(t) stays the goal. R
0
may overtake
R
1
and this behaviour is factorised under a q seq sum
node. The overtake steering behaviour uses different
steering parameters sets:
1. R
0
accelerates to 150km/h and goes to top lane:
the linear speed constraint is set to [30,42]m/s,
time samples are set to 0.1s (overtaking requires
a precise driving at this speed) and a goal G
2
(t)
added to PGuide enforces R
0
to turn left.
2. when R
0
enters in area A
2
(t) behind R
1
on the top
lane, in the same speed conditions, it stays on top
lane: a goal G
3
(t) added to PGuide is set at the
end of the top lane.
3. when R
0
enters in area A
3
(t) in front of R
1
on the
top lane, in the same speed conditions, it goes to
the bottom lane: a goal G
4
(t) added to PGuide
enforces R
0
to turn right.
4. when R
0
enters in area A
4
(t) in front of R
1
on the
bottom lane, it returns to the cruise steering be-
haviour.
Figure 7 shows the steering tree of this example. The
areas and goals associated to the motion of R
1
are il-
lustrated in Figure 8
1
.
The trajectory planning returns a solution associ-
ated to each behaviour. For instance, in Figure 9(a),
the overtake behaviour is not solved when the robot
R
2
sits in the opposite lane at the same instant: only
the follow behaviour should be applied as valid trajec-
tory. If R
2
sits further (Figure 9(b)), the overtake be-
haviour is also solved and should be applied as valid
trajectory. The overtake behaviour solution lasts 13s
whereas the follow behaviour solutions lasts 15.5s.
Once again, the resulting trajectories are better than
with DKP alone. The trajectory tree is also far less
complex than usual solutions from DKP, where a lot
of backtrack occurs before a valid trajectory is found.
Computation time is thus greatly reduced.
We presented two possible usages of our archi-
tecture, but the expressiveness of the steering pa-
rameter and TÆMS languages is high enough to de-
scribe other human-like steering behaviours. Dy-
namic changes of the acceleration or linear/angular
1
Figures 8 and 9 have been vertically upscaled ∼ 8
times.
TOWARDS COGNITIVE STEERING BEHAVIOURS FOR TWO-WHEELED ROBOTS
123
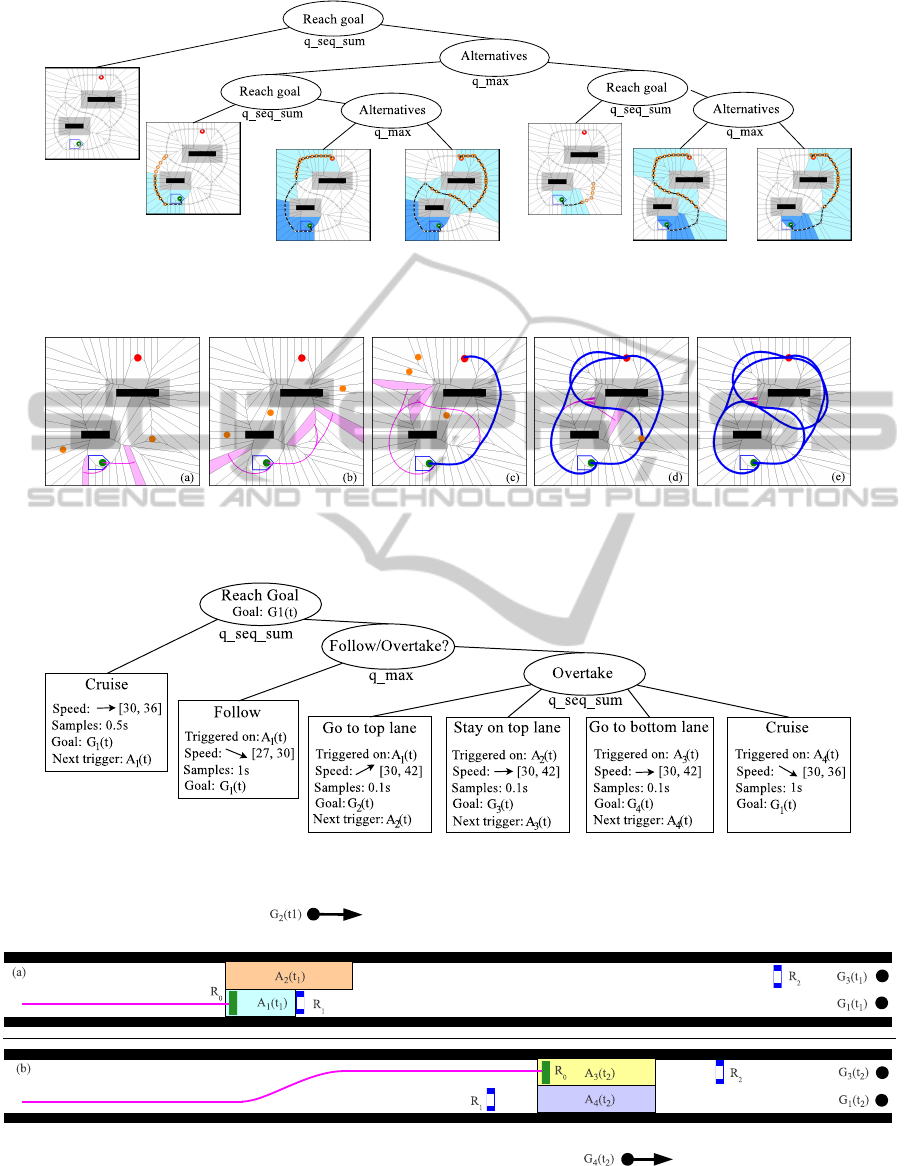
Figure 5: The steering tree for a roadmap-based guidance. Each leaf corresponds to an area, filled in cyan, in which there
is no crossing and where intermediate goals are plotted in orange. Dark blue polygons represent areas to be ignored because
they have already been visited in parent nodes.
Figure 6: The trajectory tree guided by the steering tree of Figure 5. Blue curves are the final trajectories that reach the goal.
Magenta curves are under construction or given up trajectories. Light magenta polygons correspond to arrival areas of under
construction trajectories. Orange dots are associated intermediate goals, provided by the steering tree.
Figure 7: The final steering tree for overtaking. Nodes with thick lines were created in the initial configuration of the tree.
Other nodes come from the instantiation of the Follow/Overtake pattern.
Figure 8: Overtaking areas and goals represented at different time steps. (a) at t
1
, when a candidate trajectory enters the
A
1
(t) area, (b) at t
2
, when a candidate trajectory enters the A
3
(t) area. The controlled robot is the green rectangle and the
vehicles to avoid are the blue rectangles.
ICAART 2012 - International Conference on Agents and Artificial Intelligence
124

Figure 9: Different overtaking situations. (a) R
0
, in green, cannot overtake. It must follow R
1
using the trajectory in blue.
(b) R
0
can follow or overtake R
1
and we get two alternative trajectories in blue. R
0
is drawn on the one that overtakes.
speed constraints and of the goal point could be used
to describe other driving manoeuvres and smooth or
aggressive driving behaviours.
5 CONCLUSIONS AND FUTURE
WORKS
Like Reynolds did for autonomous characters in sim-
ulated environments, we want to introduce steering
behaviours for mobile robots but using a cognitive
rather than a reactive approach. We presented an ar-
chitecture where two tightly coupled layers are used
to co-elaborate candidate trajectories that may be
evaluated by a cognitive layer to choose the best one
to apply in a particular situation.
For the first layer, we chose the DKP trajectory
planner which is able to efficiently deal with kinody-
namic constraints in a real continuous world. But, this
single layer cannot handle all the aspects governing a
good trajectory for a complex robot task. We thus
added a TÆMS based layer which role is to make the
connection between higher cognitive layers and the
trajectory planning layer. In this layer, we are able to
describe steering behaviours that constraint in a top-
down interaction the construction of the DKP trajec-
tory tree. The interaction is also bottom-up because
steering behaviours are instantiated in reaction to sit-
uations detected during the construction of the trajec-
tory tree. Detailed examples showed that this archi-
tecture is also more efficient for the solution explo-
ration than DKP alone.
Future works will focus on two main improve-
ments of this architecture. First, its ability to run con-
tinuously. For the moment, we have to launch distinct
successive planning tasks to deal with an endless sce-
nario. We may continuously grow our two trees to re-
act to new events, select nodes to execute and discard
already executed nodes. Second, we will work on a
third layer reasoning about the steering behaviours
to instantiate them for the achievement of the high
level goals of the robot and to possibly merge them.
We would be allowed to generate and evaluate com-
pound behaviours like overtake aggressively or follow
smoothly.
REFERENCES
Branicky, M., Curtiss, M., Levine, J., and Morgan, S.
(2006). Sampling-based planning, control and veri-
fication of hybrid systems. IEE Proceedings Control
Theory and Applications, 153(5):575.
Decker, K. (1996). TÆMS: A Framework for Environment
Centered Analysis & Design of Coordination Mech-
anisms. Foundations of Distributed Artificial Intelli-
gence, Chapter 16, pages 429–448.
Gaillard, F., Soulignac, M., Dinont, C., and Mathieu, P.
(2010). Deterministic kinodynamic planning. In Pro-
ceedings of the Eleventh AI*IA Symposium on Artifi-
cial Intelligence, pages 54–61.
Gaillard, F., Soulignac, M., Dinont, C., and Mathieu, P.
(2011). Deterministic kinodynamic planning with
hardware demonstrations. In Proceedings of IROS’11.
To appear.
Horling, B., Lesser, V., Vincent, R., Wagner, T., Raja, A.,
Zhang, S., Decker, K., and Garvey, A. (1999). The
TAEMS White Paper.
Jaesik, C. and Eyal, A. (2009). Combining planning and
motion planning. 2009 IEEE International Confer-
ence on Robotics and Automation.
Lacroix, B., Mathieu, P., Rouelle, V., Chaplier, J., Galle, G.,
and Kemeny, A. (2007). Towards traffic generation
with individual driver behavior model based vehicles.
In Proceedings of DSC-NA’07, pages 144–154.
Lekavy, M. and N´avrat, P. (2007). Expressivity of STRIPS-
Like and HTN-Like Planning, volume 4496/2007 of
Lecture Notes in Computer Science, pages 121–130.
Springer Berlin / Heidelberg, Berlin, Heidelberg.
McDermott, D., Ghallab, M., Howe, A., Knoblock, C.,
Ram, A., Veloso, M., Weld, D., and Wilkins, D.
(1998). Pddl-the planning domain definition language.
The AIPS-98 Planning Competition Comitee.
Reynolds, C. (1999). Steering behaviors for au-
tonomous characters. In Game Developers Confer-
ence. http://www. red3d. com/cwr/steer/gdc99.
This work is supported by the Lille Catholic Univer-
sity, as part of a project in the Handicap, Dependence and
Citizenship pole.
TOWARDS COGNITIVE STEERING BEHAVIOURS FOR TWO-WHEELED ROBOTS
125
