
A NOVEL STRUCTURE FOR REALIZING
GOAL-DIRECTED BEHAVIOR
Cem Yucelgen, Yusuf Kuyumcu and N. Serap Sengor
Electronics and Communication Engineering Department, Istanbul Technical University, Maslak, Istanbul, Turkey
Keywords: Adaptive resonance theory, Reinforcement learning, Goal-directed behaviour.
Abstract: Intelligent organisms complete goal-directed behaviour by accomplishing a series of cognitive process.
Inspired from these cognitive processes, in this work, a novel structure composed of Adaptive Resonance
Theory and an Action Selection module is introduced. This novel structure is capable of recognizing task
relevant patterns and choosing task relevant actions to complete goal-directed behavior. In order to construct
these task relevant choices the parameters of the system are modified by Reinforcement Learning. Thus the
proposed structure is capable of modifying its choices and evaluates the outcome of these choices. In order
to show the efficiency of the proposed structure word hunting task is solved.
1 INTRODUCTION
To suppress the irrelevant stimuli amongst similar
ones, to focus on the task relevant ones and to
perceive these and process them to reach a goal
requires accomplishment of a series of cognitive
processes. A system capable of realizing these
processes would be efficient in many intelligent
system applications. In this work, an integrated
structure composed of Adaptive Resonance Theory
(ART) and Action Selection module (AS) is
introduced. This novel structure named ART-AS is
capable of recognizing the changes in the
environment and is able to adapt itself to these
changes according to the rewards it obtains for its
choices. There are two different adaptation
procedures: (i) one corresponding to selective
attention where parameters of ART are modified to
recognize goal related patterns and (ii) a second
adaptation where parameters of AS module are
modified to choose task relevant actions. Both of
these adaptation procedures are accomplished by
Reinforcement Learning (RL).
In most of the applications, the differential
equations defining ART (Carpenter, Grossberg,
1987) are not considered. Instead an algorithm using
steady state behavior of these equations is utilized
(Tan, 2004). Here the overall ART-AS structure is
composed of nonlinear dynamical systems and the
behavior of each dynamical system is adapted by the
parameters governing their steady-state behavior.
So, to determine the parameters that are effective in
guiding ART’s behavior, the solution of the
differential equations are considered. Once, the
effective parameters are determined and their
interpretation are discussed they are used to guide
ART. These parameters of ART are modified by
reward expectation error and the task related patterns
are obtained in the Long Term Memory (LTM). To
order the patterns in LTM according to the task is
the last step in concluding goal-directed behavior.
This ordering of patterns in LTM is accomplished
with a set of difference equations realizing action
selection. Another dynamical system defines the AS
module which is developed considering the neural
substrates that are effective in action selection
(Sengor, Karabacak, Steinmetz, 2008). In (Sengor
et.al., 2008) it has been shown that this dynamical
system is capable of selecting task relevant actions
in a goal-directed behavior.Thus, in the proposed
ART-AS structure while ART part realizes
recognition of task relevant patterns, AS part
determines the task relevant actions.
A similar work is (Brohan, Gurney, Dudek,
2010), where a hybrid structure is proposed. In their
work Self-Organizing Maps (SOM) and RL are
incorporated. Their aim is to solve an action
selection problem while organizing SOM with
selected actions. Here, ART is considered instead of
SOM and the aim is not only to order features
according to actions but to show how pattern
249
Yucelgen C., Kuyumcu Y. and Serap Sengor N..
A NOVEL STRUCTURE FOR REALIZING GOAL-DIRECTED BEHAVIOR.
DOI: 10.5220/0003719902490255
In Proceedings of the 4th International Conference on Agents and Artificial Intelligence (ICAART-2012), pages 249-255
ISBN: 978-989-8425-95-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)
recognition can be adapted according to a goal.
Another similar work is (Tan, 2004), where ART
and RL are used together. In FALCON the main
concern is to propose machine learning methods,
while here efficiency of a system inspired by neural
substrates is investigated.
This paper is organized as following: In Section
2, a scheme for the proposed structure is given. The
RL mechanism modifying the parameters of ART-
AS is explained. Especially, the differential
equations defining ART are considered and the
effect of parameters ρ, D1, D2 and L on LTM is
investigated. In Section 3, word hunting task is
solved using the proposed structure.
2 THE PROPOSED STRUCTURE
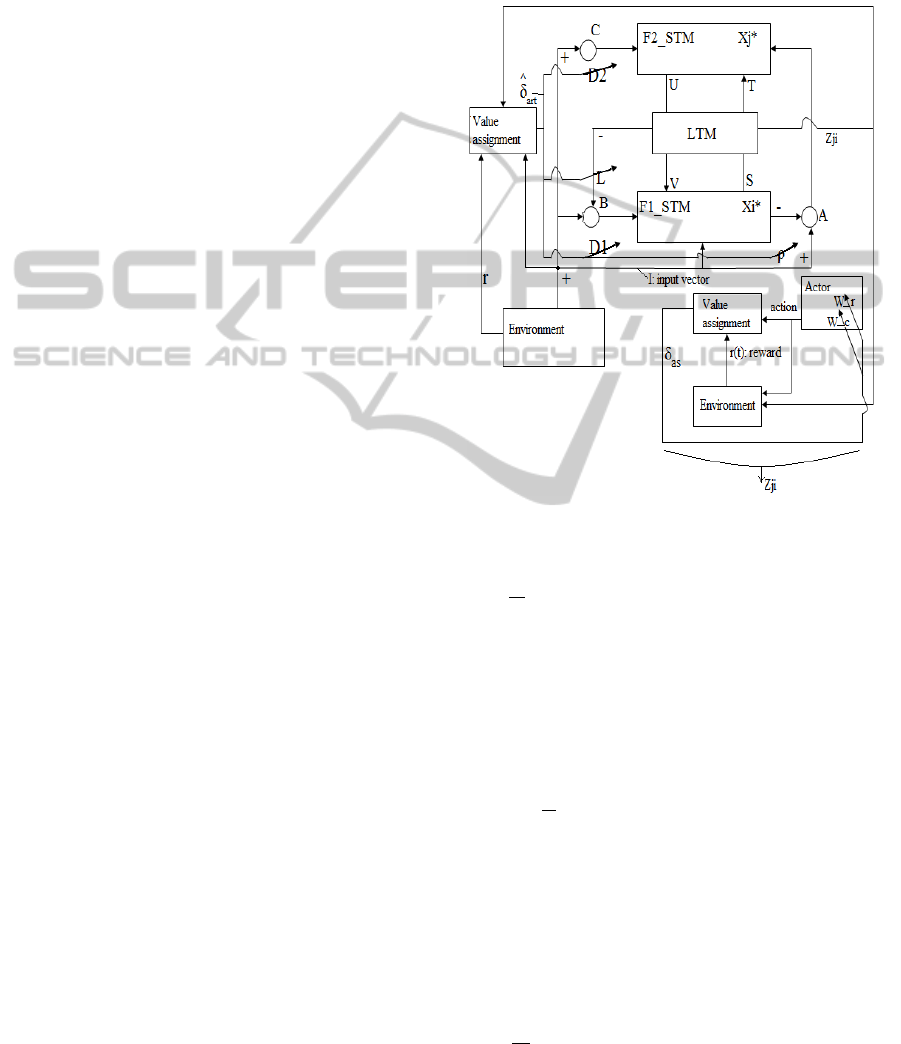
The overview of the ART-AS structure together with
learning process RL is presented in Fig.1.
In ART-AS structure, some parameters of ART
are modified by RL to realize selective pattern
recognition.
Modification of the parameters depends on the
evaluation of features at LTM by the value
assignment block. RL part does not dictate ART
what to recognize, it just assigns a value to ART’s
performance. This assigned value is evaluated by
δ
art
. If ART cannot manage to recognize the stimulus
correctly it is not rewarded, and parameter δ
art
changes the vigilance parameter ρ and parameters
D
1
, D
2
and Lwhich define the effect of
neurotransmitter dopamine.
Once, the perception of task related features is
completed, in order to conclude the goal-directed
behaviour, these features have to be processed
according to the task. The second RL component of
the proposed structure is responsible for this process.
The features in LTM are processed by the RL
block on the lower right hand side of the Fig.1. So
the environment in this part is composed of the
perceived patterns stacked at LTM. The patterns that
are chosen by ART are represented as different
states in the environment and actor selects an action
corresponding to each of these. The selected action
is evaluated by RL and the task related actions are
chosen. The error in reward expectation δ
as
modifies
a parameter of the dynamical system realizing action
selection thus stimulating actor to choose a different
action.
In this setup, while ART with the RL mechanism
performs selective pattern recognition, AS part
orders the unorganized LTM outputs according to
the goal by second RL part.
2.1 Realization of ART-AS
Once stimuli in the environment are presented to F1,
this triggers the dynamic progression in this layer
which is defined by the differential equation in Eq.1.
(Carpenter, Grossberg, 1987):
Figure 1: The proposed structure: The modification of
ART and action selection is realized by RL.
ℰ
=−
+
(
1−
)
−(
+
)
(1)
Here
=
+
is the excitatory signal. It is equal to
I
i,
as V
i
is not formed yet. J
i
-
is the inhibitory signal.
If vigilance test is not satisfied in gain control unit
A, it inhibits the F1 activities. However, in the first
step this term does not emerge as features at F1
instead approach to equilibrium point at I
i
.
Therefore, equation for layer F1becomes
ℰ
=−
+
(
1−
)
.
(2)
With X
i
*
being the solution of Eq. 2, F1 releases
signal S to the synaptic field.
=ℎ
(
∗
)
=
1,
∗
>0
0, ℎ
(3)
Bottom-up activities of LTM are triggered by S.
=
[−
+ℎ
(
)
]
(4)
ICAART 2012 - International Conference on Agents and Artificial Intelligence
250

At the end of this synaptic process, signal T which
stimulates the layer F2 is produced.
=
ℎ
(
∗
)
(5)
Dynamic process in layer F2 is defined by Eq. 6.
ℰ
=−
+1−
−(
+
)
(6)
Similar to layer F1signals
=
+
and J
j
-
are the
excitatory and inhibitory for layer F2, respectively.
J
j
+
is the excitatory signal and starts the activities at
F2. On the other hand, depending on the vigilance
test result in unit A, J
j
-
inhibitory signal is either
generated or not generated. When J
j
-
is not
generated, the equation for F2 becomes as follows:
ℰ
=−
+1−
(
+
)
(7)
With X
j
*
being a solution of Eq. 7, F2 releases signal
U to synaptic field. This signal is important as it
determines the neuron that is effective in
recognizing the patterns.
=
∗
=
1,
=max{
}
0, ℎ
(8)
Top-down synaptic activities is initiated by the
signal U and top-down weights start to take shape
through Eq. 9.
=
∗
[−
+ℎ
(
)
]
(9)
At the end of this synaptic activity, top-down
template V stimulates
=
∗
In F1 and unit B, V and I are compared to each
other. If result of this comparison exceeds the
vigilance parameter ρ, then ART reaches to stable
state and forms itself efficiently (Carpenter,
Grossberg, 1987). Otherwise, inhibitory signals are
produced and signals at layers and synaptic fields
are reset. Thus, equations for layer F1 and F2
become
ℰ
=−
+
(
1−
)
−(
+
)
(10)
ℰ
=−
+1−
−(
+
)
–
(11)
ART structure is convenient for adaptation and RL
mechanism is used to modify the parameters of
ART. The performance of ART depends on
parameters ρ, D
1
, D
2
and L. In (Dranias, Grossberg,
Bullock, 2000) it is pointed out that, the effect of
parameters D
1
, D
2
correspond to the effect of
dopamine on cognitive processes. In this work, these
parameters are modified by the reward expectation
error δ
art
. The details of this reward mechanism will
be explained in detail in (2.2).
Once the patterns formed by ART are stacked at
its LTM, these have to be evaluated according to the
goal. In order to fulfil the goal, some actions have to
be chosen and the patterns have to be processed
according to these actions. The dynamical system
given in Eq. 12 corresponds to cortico-striato-
thalamic loop proposed in (Sengor, et al., 2008). It is
shown that this system is capable of choosing task
relevant actions when parameter
r
W
is modified
according to RL.
(
+1
)
=
(
(
)
+
(
)
+
())
(
+1
)
=
(
(
)
−
(
)
)
(
+1
)
=
(
(
)
)
(
+1
)
=(
(
)
)
(
+1
)
=
(
()−
(
)
)
(
)
=0.5(tanh
(
−0.45
)
+1)
(12)
In (Sengor et al., 2008) it is discussed that
modifying
r
W
corresponds to modelling the effect
of dopamine on action selection. The details of this
RL process will be given in Section 2.2.
2.2 Learning Process for ART-AS
The solutions of the differential equations governing
ART depend on its parameters ρ, D
1
, D
2
and L. Any
change in these parameters highly affects the
behaviour of the nonlinear system. In (Dranias et.al.,
2000), it is pointed out that forming the weights to
maintain the learning process in LTM relies also on
dopamine-gated steepest descent learning. The
following two equations are related to the dopamine-
gated steepest descent learning:
=
∑
∗
=
∑
ℎ
(
∗
)
(13)
Besides parameters D
1
and D
2
, ρ has a different role
on the system. Following simulation results show
this.
As it is depicted in Fig. 2b-c, more features are
obtained with higher ρ values. Fig. 2b and d
manifest the effect of the D
1
and when D
1
increases,
the number of features formed in the LTM decrease.
The effect of D
2
is not taken into consideration as by
itself D
2
affects only layer F2. However, D
2
affects
LTM when interacts with change in L.
A NOVEL STRUCTURE FOR REALIZING GOAL-DIRECTED BEHAVIOR
251

(a) (b)
(c) (d)
Figure 2: Patterns in (a) environment (b) LTM with
ρ=0.95
, D
1
=0.2, D
2
=0.7, L=1(c) LTM with ρ=0.55,
D
1
=0.2, D
2
=0.7, L=1(d) LTM with ρ=0.95, D
1
=0.7,
D
2
=0.7, L=1.
In (Grossberg, 1999), it is shown that inactivation
and releasing of the neurotransmitters for a neuron is
based on S in Eq. 14. Using this equation the
parameter responsible for neurotransmitter
inactivation and release is obtained.
=
(
−
)
−=+
(
−−
)
(14)
Accepting that neurotransmitters release from F1
neurons, and considering z
ij
in Eq. 9. where E
ij
is
defined as in Eq. 15
=ℎ
(
)
+
ℎ(
)
(15)
gives the following result
=
−
+
ℎ
(
)
=
ℎ
(
)
+(−
ℎ
(
)
−
ℎ
(
)
)
(16)
Considering above equations, S can be obtained
in terms of parameter L.
≜
ℎ(
)
(17)
Thus, changing the ratio of the inactivation and
release of neurotransmitters for one neuron in F1
causes parameter L to have influence on ART. The
effect of parameter L can be observed in Fig. 3a
where letter “L” is associated with letter “N”. In Fig.
3b this association does not exist. Hence, increasing
parameter L results in decaying of this association
between the patterns in LTM. Also, “F” is not
formed with L=30.
Fig. 4 shows the influence of D
2
; as D
2
decrease,
letter “L” is associated with “N” again. However, in
this case letter ”G” becomes clear. Also, in Fig. 3
and Fig.4 another effect of L can be seen. In Fig.3,
“M” does not exist but is formed in Fig. 4.
Considering the results of Fig. 2-4, it can be
(a) (b)
Figure 3: Patterns in LTM with ρ=0.95, D
1
=0.35, D
2
=0.7
(a) L=1 (b) L=30.
(a) (b)
Figure 4: Patterns in LTM with ρ=0.95, D
1
=0.35, L=45
(a) D
2
=0.7 (b) D
2
=0.05.
concluded that while ρ and D
1
are effective on the
number of patterns formed in LTM, D
2
and L are
effective on clarity and formation of some patterns
in LTM. These results reveal that ART can be
modified with these four parameters. A reward
mechanism, similar to one in (Brohan, et al., 2010)
is used and the error δ
art
modifies the parameters of
ART. Owing to the fact that there is no
mathematical model introducing the relation
between δ
art
, ρ and D
1,
D
2
, empirical equations
inspired by simulation results are produced. These
equations are used to modify the parameters until
ART forms the task relevant features. These
parameters are controlled by an error parameter
obtained in value assignment block. First, in pattern
matrices (I) which are composed of “1”’s and “0”’s
the elements with value “1” are determined. Then,
the elements of LTM outputs corresponding to these
elements are determined and
""
=
|
1−
|
are calculated for each element
corresponding to “1”. These errors are summed up
for each input- output pair and smallest value is
chosen amongst them. It is named
. Equations in
(18) are determined by
which produces δ
art
according to an emprical formula,
=
ℎ
=+
=0.41−
1−
=0.12−
1−
=0.3+1.3+
1−
(18)
Once a pattern is recognized successfully, in order to
ICAART 2012 - International Conference on Agents and Artificial Intelligence
252
perceive other patterns ART’s parameter values are
reset to values which give the worst perception of
the features. If perception of the new pattern could
not be realized with these worst case values, they are
updated till they provide better results. When the
patterns related to the task are stacked at the LTM,
in order to complete the goal-directed behaviour,
these patterns are ordered by actions selected with
the dynamical system given by Eq. 12. The action
selected for a pattern is evaluated by critic. Then the
reward r(t) and expectation error
)(t
as
δ
are
determined as follows (Schultz, Dayan, Montague,
1997).
)()1()()( tVtVtrt
as
−++=
δ
(19)
where the value function
ItnWtV
v
))(()( +=
,
)(tn
is
the noise term and I corresponds to patterns in LTM.
This reward expectation error modifies the action
selection and value function by updating the
vr
WW ,
,
respectively as follows (Sengor, et al., 2008):
)()()()1( tIttWtW
asvvv
′
+=+
δ
η
)())(()()()1( tErtpfttWtW
pmpmasrrr
δ
η
+=+
(20)
To set up the representation of patterns in action
selection
c
W
is updated as
)()()()()1( tItptkWtW
pmasccc
′
+=+
δ
η
(21)
3 SIMULATION RESULTS
In order to verify the effectiveness of the proposed
hybrid structure, word hunting puzzle is considered.
In the puzzle a set of letters that can form a word
should be recognized from a jam of letters. As an
example, the template given in Fig. 5 is considered.
Figure 5: The word hunting puzzle.
The task is to recognize the letters B, D, I, R and
then organize these letters to obtain the word BIRD.
An in-house code written in MATLAB
®
as an m-file
is used. For ART, the initial values of weights and
x
i
, are random positive and negative small numbers.
Coefficient matrices, A
1
, C
1
and A
2
, C
2
are unit
matrices which have dimensions same as the input
patterns. B
1
and B
2
are column vectors with
dimensions same as the patterns and their
components are random small positive numbers. All
layers’equationsaresolvedoutbyusingOpen
EulerMethodsoisstepsizeanditsvalueis
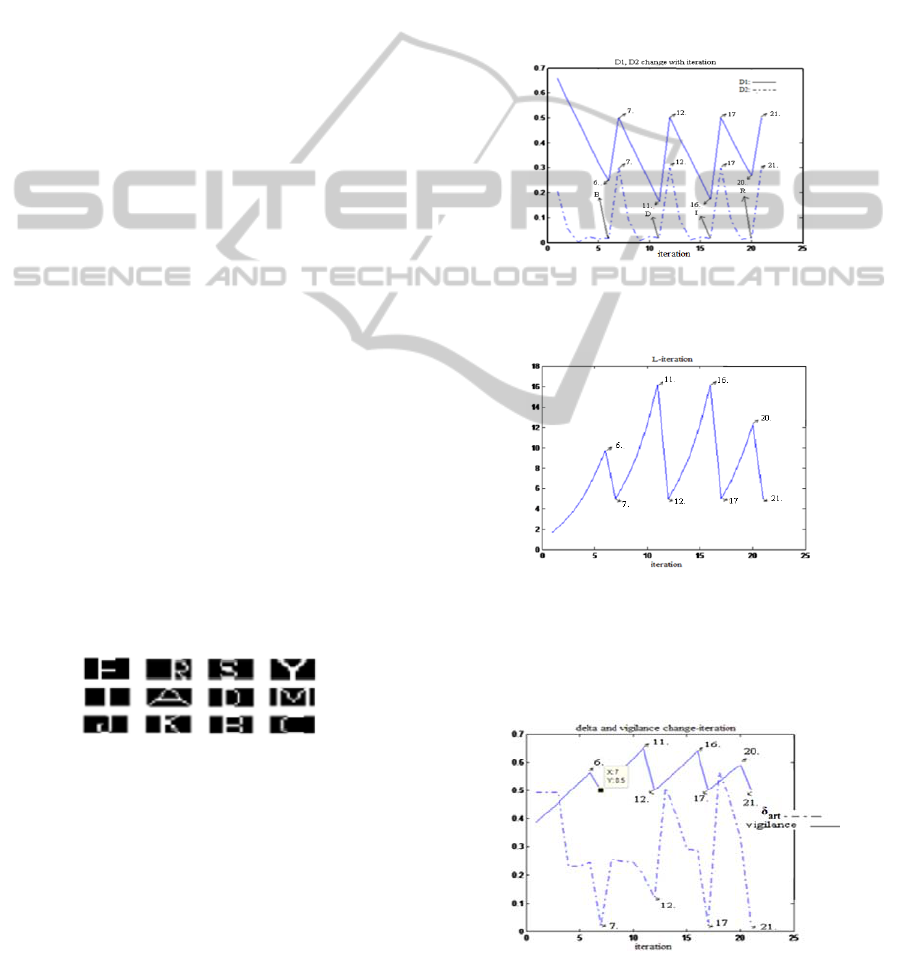
0.03.The initial values of parameters are ρ=0.35,
L=1, D
1
=0.75, D
2
=0.6. The evaluation of D
1
and D
2
and L through the learning procedure is shown in
Fig.6 and 7, respectively. In Fig. 8, the evaluation of
δ
art
and vigilance parameter ρ is given. For example,
in Fig. 6 from 1
st
to 6
th
iteration, ART cannot
perceive the “B” letter but in 7
th
iteration δ
art
becomes less than 0.15
which is the reward level. In
this case, ART is rewarded and “B” is stacked in the
LTM.
Figure 6: For 6
th
11
th
16 and 20
th
iterations, letters are
about to be learned. After learning, at iterations 7, 12, 17
and 21 D1 and D2 are set to 0.5 and 0.3, respectively.
Figure 7: At 6
th
, 11
th
, 16
th
and 20
th
iterations, letters are
determined. For 7
th
, 12
th
, 17
th
and 21
th
iterations L is set to
5.
Here it must be noted that only the recognized letters
are stacked at LTM as given in Fig. 9.
Figure 8: For 6
th
, 11
th
, 16
th
and 20
th
iterations, letters are
determined. At 7
th
, 12
th
, 17
th
and 21
th
iterations, ρ is set to
0.5. Also, at these iterations, δ
art
has the lowest values.
A NOVEL STRUCTURE FOR REALIZING GOAL-DIRECTED BEHAVIOR
253
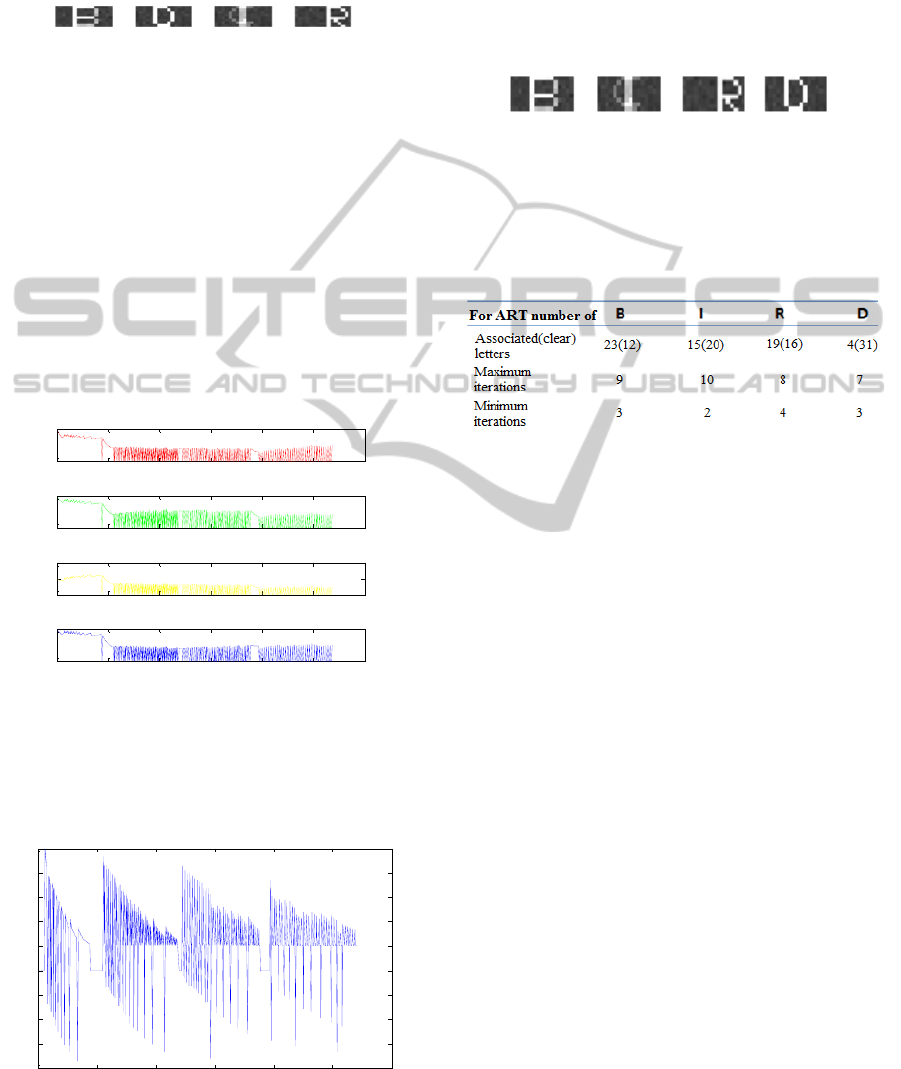
As it can be seen in the third block in Fig. 9, letter
“I” and “B” are associated with letter “C” and “F”
respectively, but as this association do not
mix, “I”
and “B”, they are accepted. Once all letters are
stacked then RL organizes them to form the word.
Figure 9: The patterns in LTM.
The ordering of these letters to form a word is
accomplished by action selection system which
adapts action selection according to RL. The initial
values of the parameters
r
W
,
C
W
and
V
W
are small
random numbers and the reward is 1 when a correct
choice is done for a letter and it is assumed that the
correct choice is set up if reward is obtained 20
times, successively. Each time the correct place of a
letter in the word is determined, the next letter is
considered. The change in values of
r
W
and
)(t
as
δ
can be followed from Fig.10 and Fig.11,
respectively. In 35 trials the average and mean
number of the iterations is 428±86.13.
Figure 10: Updating of wr during RL.
As it is depicted in Fig.11, for each of the four letters
)(t
as
δ
fluctuates during the search for the correct
place but once the correct place for the letter
Figure 11: Change of
)(t
as
δ
during RL.
is found,
)(t
as
δ
does not change anymore and also
the value of
r
W
is stabilized. Once the place of a
letter is determined correctly, search begins for the
next letter and fluctuation in
)(t
as
δ
begins again.
When the action selection process is completed the
letters are organized to form the word as shown in
Fig. 12.
Figure 12: The patterns ordered by action choices.
In order to see the effect of random initial valued
weights, the problem is solved for 35 times. These
results are shown in Table 1.
Table 1: ART’ s performance for 35 tests.
4 CONCLUSIONS
In this work a novel structure combining ART and
AS module is proposed. It is shown that ART-AS
recognizes task related patterns and fulfils goal-
directed behaviour. To confirm this property of
ART, the analysis of the ART structure is given in
detail considering differential equations defining it.
The performance is tested with word hunting task
and the simulation results are discussed.
REFERENCES
Carpenter, G. A., Grossberg, S., ‘’A Massively Parallel
Architecture for a Self Organizing Neural Pattern
Recognition Machine’’, Computer Vision, Graphics,
and Image Processing Vol. 37, 1987.
Sengor, N. S., Karabacak, O., Steinmetz, U., “A
Computational Model of Cortico-Striato-Thalamic
Circuits in Goal-Directed Behaviour”, Proc.
ICANN’08, 2008.
Brohan, K., Gurney, K., Dudek, P., “Using Reinforcement
Learning to Guide the Development of Self Organised
Feature Maps for Visual Orienting”, Proc. ICANN’10,
2010.
Tan, A. H., “FALCON: A Fusion Architecture for
Learning, Cognition and Navigation”, Proc. IJCNN,
2004.
0 100 200 300 400 500 600
0
0.5
Change of Weights
0 100 200 300 400 500 600
0
0.5
0 100 200 300 400 500 600
0
0.5
1
W
r
0 100 200 300 400 500 600
0
0.5
Iteration
0 100 200 300 400 500 600
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
Reinforcement Signal - delta
Iteration
Value
ICAART 2012 - International Conference on Agents and Artificial Intelligence
254

Dranias, M. R., Grossberg, S., Bullock, D.,
“Dopaminergic and non-dopaminergic value systems
in conditioning and outcome specific revaluation”,
2000.
Schultz, W., Dayan P., Montague, P. R., “A Neural
Substrate of Prediction and Reward”, Science, Vol.
275, 1997.
Grossberg, S.,“Neural models of normal and abnormal
behavior: what do schizophrenia parkinsonism,
attention deficit disorder, and depression have in
common?” Progress in Brain Research, Vol 121,
1999
A NOVEL STRUCTURE FOR REALIZING GOAL-DIRECTED BEHAVIOR
255
