PROBABILISTIC ESTIMATION OF VAPNIK-CHERVONENKIS

DIMENSION

Przemysław Kle¸sk

Department of Methods of Artiﬁcial Intelligence and Applied Mathematics, West Pomeranian University of Technology

ul.

Zolnierska 49, Szczecin, Poland

Keywords:

Statistical learning theory, Machine-learning, Vapnik-Chervonenkis dimension, Binary classiﬁcation.

Abstract:

We present an idea of probabilistic estimation of Vapnik-Chervonenkis dimension given a set of indicator

functions. The idea is embedded in two algorithms we propose — named A and A

′

. Both algorithms are based

on an approach that can be described as expand or divide and conquer. Also, algorithms are parametrized

by probabilistic constraints expressed in a form of (ε,δ)-precision. The precision implies how often and by

how much the estimate can deviate from the true VC-dimension. Analysis of convergence and computational

complexity for proposed algorithms is also presented.

1 INTRODUCTION

Vapnik-Chervonenkis dimension is an important no-

tion within Statistical Learning Theory (Vapnik and

Chervonenkis, 1968; Vapnik and Chervonenkis,

1989; Vapnik, 1995; Vapnik, 1998). Many bounds

on generalization or sample complexity are based on

it.

Recently, several other measures of functions sets

capacity (richness) have been under study. Particu-

larly, of great interest are covering numbers (Bartlett

et al., 1997; Anthony and Bartlett, 2009). In many

cases covering numbers can lead to tighter bounds

(on generalization or sample complexity) than pes-

simistic bounds based on VC-dimension. However,

the constructive derivation of covering numbers itself

is usually a challenge. One has to suitably take ad-

vantage of some properties of given set of functions

or of the learning algorithm and discover how they

translate onto a cover. One of such attractive results is

e.g. a result from (Zhang, 2002) related to regulariza-

tion. Qualitatively, it states that for sets of functions

linear in parameters and under a L

-regularization

(general q = 1,2,...) the bound on covering number

scales only linearly with the dimension of input do-

main. This allows to learn and generalize well with

a sample complexity logarithmic in the number of at-

tributes. On the other hand, there exist results where

the property used for the derivation of covering num-

bers is actually the known VC-dimension of some

set of functions (Anthony and Bartlett, 2009), which

again proves its usefulness.

Known are some sets of functions for which the

exact value of VC-dimension has been established

by suitable combinatorial or geometric proofs (of-

ten very complex). Here are some examples. For

polynomials deﬁned over R

of degree at most n,

the VC-dim is



n+d



, see e.g. (Anthony and Bartlett,

2009). For hyperplanes in R

(which can be bases

for multilayer perceptrons) the VC-dim is d + 1 (Vap-

nik, 1998). For rectangles in R

the VC-dim is 2d

(Cherkassky and Mulier, 1998). For spheres in R

(which can be bases of RBF neural networks) the

VC-dim is d + 1 (Cherkassky and Mulier, 1998). As

regards linear combinations of bases as above the

VC-dim can typically be bounded by the number of

bases times the VC-dim of a single base (Anthony and

Bartlett, 2009, p. 154), this fact however requires usu-

ally a careful analysis.

Also, some analysis has been done in the subject

of computational complexity for the VC-dimension.

In particular, in (Papadimitriou and Yannakakis,

1996) authors take up the following problem ,,given

a set of functions F and a natural number k, is

VC-dim(F) ≥ k?”, i.e. one asks about a lower bound

of VC-dimension. And the problem is proved to be

logNP-complete.

Our motivation for this paper is to introduce an

idea for algorithms, which given an arbitrary set of

functions (plus a learning algorithm) would be able

to estimate its VC-dimension with an imposed proba-

bilistic accuracy. Such algorithms, if sufﬁciently suc-

262

Klesk P..

PROBABILISTIC ESTIMATION OF VAPNIK-CHERVONENKIS DIMENSION.

DOI: 10.5220/0003721702620270

In Proceedings of the 4th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2012), pages 262-270

ISBN: 978-989-8425-95-9

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

cessful, could potentially replace the need for com-

plex proofs establishing the exact value of the VC-

dimension.

2 NOTATION, NOTIONS, TOOLS

We restrict considerations to the binary classiﬁcation

learning problems.

Let F denote the set of indicator functions

, which

we have at disposal for learning. Let L denote the

learning algorithm we use to choose a single function

from F. This happens via the sample error minimiza-

tion

principle.

Let P denote the unknown joint probability distri-

bution deﬁned over Z = X × Y from which training

pairs z = (x, y) are drawn, where in general x ∈ R

are input points and y ∈ {0,1} are corresponding class

labels. By z = {z

,...,z

} we shall denote the

whole training sample of size m drawn from the prod-

uct distribution P

in a i.i.d. manner

For any ﬁxed function f ∈ F the true generaliza-

tion error with respect to P is typically calculated as

( f) =

(z)dP(z), (1)

where l

is the following loss function

(z) = l



(x,y)



(

0, for f(x) = y;

1, for f(x) 6= y.

(2)

Therefore er

( f) expresses the probability of misclas-

siﬁcation of (x,y) drawn randomly from P. Since

P is unknown the learning algorithm L can only try

to minimize the frequency of misclassiﬁcation on the

observed sample i.e.:

( f) =

∑

i=1

). (3)

Let the solution-function of L be denoted by

We now brieﬂy remind some notions introduced

by Vapnik. Let l

= {l

: f ∈ F} denote the set of loss

functions generated by F. Consider the following set



),...,l

)



: f ∈ F



. (4)

It contains all distinguishable functions in l

re-

stricted to the ﬁxed sample z

,...,z

. Throughout the

paper we shall denote (4) by (l

)

,...,z

{0,1}-valued functions.

Alternatively also called empirical risk minimization

Independent, identically distributed. This means P

unknown but ﬁxed.

Using a natural correspondence between indica-

tor functions and dichotomies of a set, Vapnik intro-

duces the notion of shattering. We say that l

shat-

ters a sample z

,...,z

if all its dichotomies can be

generated using functions from F, equivalently this

means that the number of distinguishable functions is

#(l

)

,...,z

= 2

. The Vapnik-Chervonenkis dimen-

sion for l

(or equivalently for F) is equal to the size

of some largest sample that can be shattered.

It will be helpful to remind three more quantities:

• Vapnik-Chervonenkis entropy

(m) =

ln#(l

)

,...,z

(5)

which is an expectation of the logarithm of the

number of distinguishable functions;

• annealed entropy

ann

(m) = ln

#(l

)

,...,z

(6)

which is a logarithm of expected number of dis-

tinguishable functions;

• growth function

(m) = sup

,...,z

#(l

)

,...,z

, (7)

which is supremum number of distinguishable

functions.

Known is the connection H

(m) ≤ H

ann

(m) ≤

lnG

(m), where the ﬁrst inequality is due to Jensen

inequality. Known also is the fact, that VC-dim(F) is

equal to such an argument of G

after which it stops

growing exponentially.

As a tool, throughout the paper, we shall exten-

sively take advantage of one-sided Chernoff inequali-

ties (Hellman and Raviv, 1970; Schmidt et al., 1995),

which we now write down the following way

p− ν

≤

−lnδ

, (8)

− p ≤

−lnδ

, (9)

where p is a probability of some event (that will be

of interest for us) and ν

is its frequency observed in

m independent trials. Each inequality holds true with

probability

at least 1− δ.

Also, in several places we are going to take ad-

vantage of Iverson notation [s], which returns 1 if the

statement s is true and 0 otherwise (Graham et al.,

2002).

The 1−δ is an outer probability calculated with respect

to probabilistic space deﬁned over all random experiments

consisting of m independent trials.

PROBABILISTIC ESTIMATION OF VAPNIK-CHERVONENKIS DIMENSION

263

3 PROBABILISTIC SHATTERING

In this section we introduce several new notions,

which can be regarded as probabilistic versions of se-

lected notions reminded in the previous section. The

new notions are suitable for our purposes and give a

high-levelintuition on algorithms we are about to pro-

pose.

3.1 Distribution Dependence — Two

Conceptual Scenarios

We start with the following remark. It is the fact

that: shattering, growth function and VC-dimension

are distribution-independent notions. For our pur-

poses it will be convenient though to deﬁne notions

that are distribution-dependent, because we are going

to carry out probabilistic estimations. All the notions

shall therefore refer to P or P

. Two conceptual sce-

narios are possible here.

I. In this scenario we think of P as it was originally

deﬁned — i.e. the joint probability distribution de-

ﬁned over X× Y describing the speciﬁc learning

problem. And therefore we should treat all new

notions as distribution-dependent counterparts of

classical Vapnik’s notions.

II. In this scenario we conceptually replace P by

the uniform distribution. By doing so we sep-

arate ourselves from the speciﬁc problem. For

this purpose, we only need to assume a bound-

edness of X. The P will still explicitly appear

in the notions and formulas. But, we can then

agree (as a form of convention) to look at the no-

tions as distribution-independent or at least ‘orig-

inal problem’-distribution-independent, since the

uniformness does not favor any samples.

The reader can therefore treat further considera-

tions in either context — of scenario I or II. In both

scenarios we shall assume that we can freely and nu-

merously redraw samples from P.

3.2 New Notions

Deﬁnition 1. We say that µ

(m) is a shatterability

measure with respect to the probability distribution

, and is calculated as follows

(m) =

[#(l

)

,...,z

= 2

]dP

,...,z

(10)

Intuitively the shatterability measure expresses

how frequently one ‘comes across’ samples drawn

from P

which can be shattered. We suggest to

think of shatterability measure in conjunction with

the growth function G

(m), see (7). Imagine some

method trying to discover the argument z

,...,z

for which the supremum is attained. Of course for

strictness, we must remind that ﬁrstly the deﬁnition of

(m) is distribution-independent and secondly even

if it was distribution-dependent then the supremum

could be attained on sets of measure zero. Never-

theless, the intuition that the smaller µ

(m) the more

difﬁcult it is to indicate the supremum represented by

(m) is true. In particular if G

(m) < 2

then cer-

tainly µ

(m) = 0.

Deﬁnition 2. We say that a set of indicator functions

F is an m-shatterer with respect to P

(or: shatters

some samples of size m drawn from P

) if µ

(m) > 0.

Deﬁnition 3. We say that a set of indicator functions

F is not an m-shatterer with respect to P

everywhere,

if the two conditions are met:

1. µ

(m) = 0,

2. ∄ z

,...,z

such that #(l

)

,...,z

= 2

Deﬁnition 4. We say that a set of indicator functions

F is not an m-shatterer with respect to P

almost ev-

erywhere, if the two conditions are met:

1. ∃ z

,...,z

such that #(l

)

,...,z

= 2

2. µ

(m) = 0.

The complementary deﬁnitions above followfrom

the arguments discussed earlier, and the almost every-

where condition takes into account that the case where

dichotomies are feasible but for sets (samples) of

measure zero.

3.3 Probabilistic Estimation of

VC-dimension — Sketch of Idea

We now sketch an idea according to which the algo-

rithms to be presented later shall work.

Suppose that for given sample of size m we exe-

cute multiple times (say n times) an experiment con-

sisting of drawing a sample z

,...,z

from P

and

checking exhaustively if all its dichotomies are fea-

sible, i.e. checking if #(l

)

,...,z

= 2

. If for any

experiment this is true, then we can stop (before n is

reached), since certainly VCdim(F) ≥ m and we can

try to increase the sample size. If this event did not

occur in any experiment, then by means of Chernoff

inequality we have that with probability at least 1− δ:

(m) ≤ 0+

−lnδ

. (11)

We write down 0 explicitly on purpose — it is the

observed frequency of the event ‘all dichotomies are

ICAART 2012 - International Conference on Agents and Artificial Intelligence

264

feasible on random sample’. In that case we shall de-

crease the sample size. We would also like to intro-

duce a probabilistic precision parameter for the algo-

rithm. We name it (ε,δ)-precision, 0 < ε,δ < 1. If we

insert ε :=

−lnδ/(2n), it follows that the needed

number of experiments is n = ⌈− lnδ/(2ε

)⌉.

Now, by analogy to the deﬁnition 4, we introduce

the following deﬁnition.

Deﬁnition 5. We say that a set of indicator functions

F is not a (m, ε,δ)-shatterer with respect to P

if with

probability at least 1− δ:

(m) ≤ ε.

In simple words we say (with an imposed proba-

bilistic precision) that F does not shatter samples of

size m, if the probability that 2

dichotomies on a ran-

dom sample are feasible is suitably small.

Now, we deﬁne the probabilistic VC-dimension.

Deﬁnition 6. We say that the probabilistic

(ε,δ)-VC-dimension for the set F equals m, we

write

VCdim

ε,δ

(F) = m,

if there exists a sample of size m that can be

shattered by F and simultaneously F is not a

(m+ 1,ε,δ)-shatterer.

4 ALGORITHM A

The algorithm A, we are about to propose, returns the

probabilistic dimension VCdim

ε,δ

(F). This value is

an estimate of the true VC-dimension.

First, we present an auxiliary algorithm called B,

which will be invoked by the main algorithm A in a

loop. The algorithm B works as the checker of feasi-

bility of all dichotomies given a ﬁxed sample, accord-

ingly to the sketch from the section 3.3. The algo-

rithm returns 1 when all dichotomies are feasible and

0 otherwise.

B(F;z

,...,z

)

1. For all (t

,...,t

) ∈ {0,1}

1.1. Create a temporary training sample S =

),...,(x

) and execute learning algo-

rithm L on it, which yields

1.2. If

(

f) > 0 return 0.

2. Return 1.

Figure 1: Auxiliary algorithm B.

We now present the algorithm A which works with

an imposed (ε,δ)-precision, see the Fig. 2. As argu-

ments for A, apart from F we also enlist P, with solely

such an intention that we will be able to draw multiple

samples from it, nothing more (since P in general can

be unknown, recall scenario I).

ε,δ

(F, P)

1. Set m

:= 1, m

:= ∞, m := m

2. Repeat while m

− m

> 1:

2.1. Set s := 0.

2.2. Repeat n = ⌈−lnδ/(2ε

)⌉ times:

2.2.1 Draw a sample z

,.. .,z

from P

2.2.2 If B(F;z

,.. .,z

) = 1 then set s := 1 and jump

out of the loop 2.2.

2.3 If m

= ∞:

2.3.1 If s = 1 then set m

:= 2m, m := m

2.3.2 Else set m

:= 1/2m, m

:= m, m := (m

)/2.

2.4 Else

2.4.1 If s = 1 then set m

:= m, m := (m

+ m

)/2.

2.4.2 Else set m

:= m, m := (m

+ m

)/2.

3. Return ⌊m

⌋.

Figure 2: Algorithm A.

The algorithm uses an approach that could be de-

scribed as expand or divide and conquer. At the start

we set the lower bound m

and the current sample size

m to 1, whereas we set the upper bound m

to inﬁn-

ity. At ﬁrst, as the algorithm progresses and all di-

chotomies prove feasible (s ﬂag equals 1), the tested

sample sizes are doubled (step 2.3.1.). Let us call it

the expand-phase. When a moment is reached such

that all dichotomies are not feasible despite n trials,

the algorithm suitably sets m

and m

(no longer in-

ﬁnite) and puts the next sample size m to be tested in

the middle of m

and m

(step 2.3.2.). This moment

starts the divide-phase. Since then, all next execu-

tions of the main loop (step 2) make the algorithm

enter step 2.4. and suitably narrow down the interval

) until the stop condition is reached.

The form of the return value ⌊m

⌋ requires a short

explanation. The ﬂoor function is meant to handle

the special case when after the ﬁrst iteration of the

main loop (step 2.) the s ﬂag is already equal 0. Then

halfening (step 2.3.2.) causes m

to be 1/2, and since

the stop condition is reached we want to correct this

value to 0.

5 CONVERGENCE AND

COMPUTATIONAL

COMPLEXITY ANALYSIS

We will show that it is convenient to analyze con-

PROBABILISTIC ESTIMATION OF VAPNIK-CHERVONENKIS DIMENSION

265

vergence of the algorithm A in terms of shatterability

measures for given problem.

5.1 Sequence of Shatterability Measures

— General Observations

Consider the sequence of shatterability measures

along growing sample size:

(1),µ

(2),....

A moment of thought leads to the following observa-

tion.

Lemma 1. The sequence µ

(1),µ

(2),... is non-

increasing.

Proof. By independence and Fubini’s theorem we

have that:

(m+ 1)

m+1

[#(l

)

,...,z

m+1

= 2

m+1

]dP

m+1

,... ,z

m+1

)

[#(l

)

,...,z

m+1

= 2

m+1

]dP

,... ,z

)dP(z

m+1

)

≤

[#(l

)

,...,z

= 2

]dP

,... ,z

)dP(z

m+1

)

≤ µ

(m)

dP(z

m+1

Please note that in the second equality-pass any z

can be taken outside the inner integral, not necessarily

m+1

, and the rest of the proof is still valid.

A second obvious observation is that µ

(m) = 0

for all m > VCdim(F). This follows from the deﬁni-

tion of VC-dimension.

A more interesting fact is that there exist

sets of functions F and distributions P for which

the sequence complies with the following pattern:

(1,... , 1,0,...). It means the sequence consists solely

of starting ones and after some point zeros take place.

Consider e.g. hyperplanes on a plane. Clearly any sin-

gle point or two points can be shattered by a hyper-

plane. Any three points can also be shattered provided

that they do not lie in the same line. This is called

a “general position”, see e.g. (Anthony and Bartlett,

2009, Theorem 3.1), (Wenocur and Dudley, 1981).

But even so, the situation of three points lying in the

same line is of probability measure zero in continuous

spaces. Therefore the sequence for that case would

be (1,1,1,0,. . .). On the other hand it is possible to

indicate certain sets F and distributions P for which

the sequence that does not consist solely of ones and

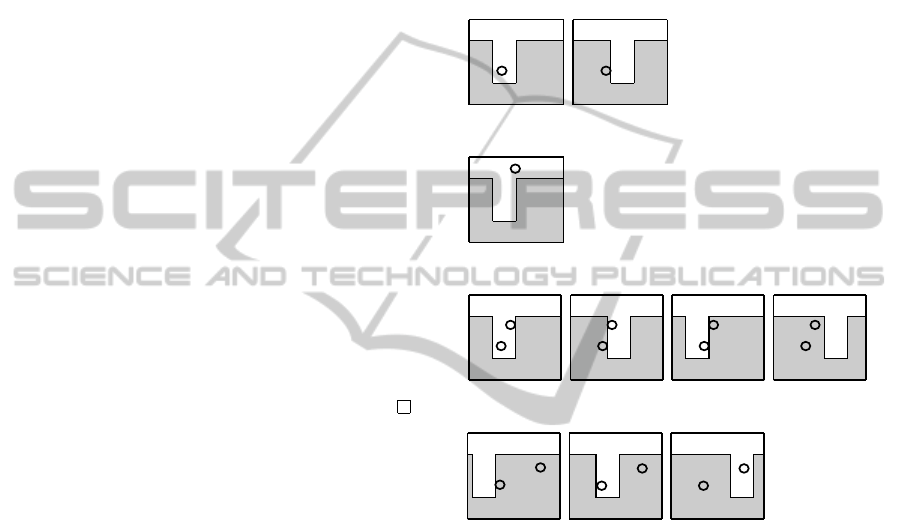
zeros. As an example see the Fig. 3. It illustrates a

set of functions deﬁned over a plane with the decision

boundary in the shape of ‘U’ letter. Suppose ‘U’ is

of ﬁxed width and height and it can be shifted only

along horizontal axes. As the ﬁgure shows there exist

samples of size m = 1 (with positive probability mea-

sure) for which only 1 dichotomy is feasible. Also,

there exist such samples (also with positive proba-

bility measure) for which 2 dichotomies are feasible.

The same is true for the case of m = 2. Therefore, the

corresponding shatterability measures must be frac-

tions.

(a) m = 1; all dichotomies feasible

(b) m = 1; not all dichotomies feasible

(d) m = 2; not all dichotomies feasible

Figure 3: Set of functions with horizontally shifting ‘U’-

shaped decision boundary of ﬁxed width. Illustration of

feasibility of all dichotomies for different samples.

From now one, for shortness we will denote the

sequence by µ

,µ

,....

5.2 Results Distribution and

Convergence for Algorithm A

As one may note, the result of algorithm A being

VCdim

ε,δ

(F) cannot be an overestimation of the true

VCdim(F), but it might be its underestimation. In

this section we analyze how often this underestima-

tion takes place and in effect we derive the probabil-

ity distribution deﬁned over the results to which A can

converge. The analysis is carried out in terms of the

sequence µ

,µ

,....

Let p(h) denote the probability that A returns

VCdim

ε,δ

(F) = h and let us start by taking a closer

look at small cases. For h = 0 we have

ICAART 2012 - International Conference on Agents and Artificial Intelligence

266

p(0) = (1− µ

)

, (12)

since it requires that in all n = ⌈− lnδ/(2ε

)⌉ inde-

pendent trials the event opposite to feasibility of all

dichotomies occurs (in n times the algorithm B re-

turned 0). For h = 1 we have

p(1) =



1− (1− µ

)



(1− µ

)

. (13)

The ﬁrst factor arises as a complement of p(0) —

the algorithm discovered that for some sample of size

m = 1 all dichotomies were feasible, but it failed to

discover such property for m = 2, hence the second

factor. The cases of h = 2, 3 reveal more of the ex-

pand or divide and conquer approach:

p(2) =



1− (1− µ

)



1− (1− µ

)



(1− µ

)

(1− µ

)

. (14)

p(3) =



1− (1− µ

)



1− (1− µ

)



(1− µ

)



1− (1− µ

)



, (15)

After the algorithm failed to discover feasibility of all

dichotomies for m = 4, it had to make a jump back-

wards to check the case of m = 3. We now move to a

bigger case example of h = 21 which illustrates well

forward and backward jumps during the divide phase

in a chronological order (see indices of µ).

p(21) =



1−(1−µ

)



1−(1−µ

)



1−(1−µ

)





1− (1− µ

)



1− (1− µ

)



(1− µ

)

(1− µ

)



1− (1− µ

)



(1− µ

)



1− (1− µ

)



(16)

A careful analysis allows to ﬁnd a regular formula for

the whole distribution. We state it as the following

theorem.

Theorem 1. Suppose µ

,µ

,... is the sequence of

shatterability measures for given set of functions

F and distribution P. Let q = ⌊log

h⌋ and let

q−1

,...,h

)

denote a binary representation for

each h > 0. Then, the probability distribution of re-

sults to which algorithm A may converge is:

p(0) = (1− µ

)

p(1) =



1− (1− µ

)



(1− µ

)

p(h) =

∏

k=0



1− (1− µ

)



(1− µ

q+1

)

q−1

∏

k=0



q−k−1

+ (−1)

q−k−1

(1− µ

i(h,k)

)



(17)

for h ≥ 2, where

i(h,k) =

q+1

+ 2

) +

∑

j=1

(−1)

1−h

q− j

· 2

q− j−1

(18)

Sketch of proof. Note that during the expand phase

the algorithm performs ⌊log

h⌋ + 2 iterations (which

is q+ 2) and this is represented in p(h) by the product

∏

k=0



1− (1− µ

)



(1− µ

q+1

)

. In this product all

but last factors must be of form 1 − (1− µ

)

, since

the algorithm discovered that some sample of size 2

can be shattered, whereas the last factor must be of

form (1 − µ

q+1

)

, since in n trials samples of size

q+1

failed to be shattered. In the divide phase the al-

gorithm performs log

q+1

− 2

) = q iterations, this

is represented by the remaining product. The i(h,k)

function handles suitably successive indices visited

by the algorithm and it is easy to check that these in-

dices are determined by the q− 1 least signiﬁcant bits

in the binary representation (h

q−1

,...,h

)

. These

bits determine also whether the factor should be of

form (1− µ

i(h,k)

)

or 1− (1− µ

i(h,k)

)

The following statements are direct consequences

of p(h) distribution.

Corollary 1. Suppose that VCdim(F) = h

∗

and sup-

pose the sequence of shatterability measures for given

F and P consists solely of ones and zeros. Then dis-

tribution of results is p(h

∗

) = 1 and p(h) = 0 for all

h 6= h

∗

. Therefore, for any 0 < ε,δ < 1 we have that

ε,δ

(F,P) = h

∗

This states that the algorithm A always converges

to the true Vapnik-Chervonenkis dimension if the se-

quence of shatterability measures does not contain

fractions.

Corollary 2. Suppose that VCdim(F) = h

∗

and sup-

pose the sequence of shatterability measures contains

fractions. Then the expected result is EA

ε,δ

(F,P) <

∗

, where expectation is taken over inﬁnite number of

runs of algorithm A for given problem.

This states that the algorithm A underestimates the

true Vapnik-Chervonenkis dimension if the sequence

of shatterability measures does contain fractions.

5.3 Computational Complexity

It is easy to see that the number of iterations of the

main loop in algorithm A (step 2.) is logarithmic as a

function of the true VCdim(F) = h

∗

. The number of

iterations is at most 2log

∗

+ 2. Recall that there are

q+ 2 iterations needed by the expand phase and q it-

erations by the divide phase. Unfortunately the most

heavy step is the execution of the algorithm B (step

2.2.2.), since it is an exhaustive check of feasibility of

all dichotomies. Therefore if we consider the compu-

tational complexity as a function of ε,δ,h

∗

then the

pessimistic number of iterations

PROBABILISTIC ESTIMATION OF VAPNIK-CHERVONENKIS DIMENSION

267

∑

visited indices

of µ

≤ n

∗

∑

i=1

= O



n(2

∗

− 1)



, (19)

which is exponential in h

∗

. This is a consequence of

the fact the B is an exact algorithm.

In the next section we propose a new algorithm

named A

′

. It is very similar to A but uses an auxiliary

algorithm B

′

being a softened probabilistic version of

B. This leads to a constant (at most) complexity of the

step 2.1.2. and in effect logarithmic complexity of the

whole algorithm.

6 ALGORITHM A

′

First, we formulate a probabilistic auxiliary algorithm

′

. For a ﬁxed sample z

,...,z

consider the follow-

ing quantity: η

,...,z

) deﬁned as the probabil-

ity that a random dichotomy drawn from the uniform

distribution (deﬁned over {0, 1}

) is feasible by some

function in F on z

,...,z

) = (20)

−1

∑

i=0

[∃ f ∈ F realizing dichotomy

m−1

,...,i

)

on z

,...,z

], (21)

where (i

m−1

,...,i

)

is a binary representation of i.

We shall introduce an additional (ε,δ)-precision.

Suppose we would like to have B

′

ε,δ

(F;z

,...,z

) =

0 if an unfeasible dichotomy occurred, and to have

′

ε,δ

(F;z

,...,z

) = 1 if with probability at least 1−δ

,...,z

) ≥ 1− ε (22)

holds true.

The algorithm B

′

is presented in the Fig. 4.

′

ε,δ

(F;z

,...,z

)

1. Repeat N = − lnδ/(2ε

) times:

1.1. Draw a random dichotomy (t

,...,t

) from a

uniform distribution.

1.2. Create a temporary training sample S =

),...,(x

) and execute learning algo-

rithm L on it, which yields

1.3. If

(

f) > 0 return 0.

2. Return 1.

Figure 4: Auxiliary algorithm B

′

We now present the algorithm A

′

. Since the inner

auxiliary algorithm was probabilistically softened, the

′

,δ

,ε

,δ

(F,P)

1. Set m

:= 1, m

:= ∞, m := m

2. Repeat while m

− m

> 1:

2.1. Set s := 0.

2.2. Repeat n = ⌈−lnδ

/(2ε

)⌉ times:

2.2.1 Draw a sample z

,...,z

from P

2.2.2 If B

′

,δ

(F;z

,...,z

) = 1 then set s := 1 and

jump out of the loop 2.2.

2.3 If m

= ∞:

2.3.1 If s = 1 then set m

:= 2m, m := m

2.3.2 Else set m

:= 1/2m, m

:= m, m := (m

)/2.

2.4 Else

2.4.1 If s = 1 then set m

:= m, m := (m

+ m

)/2.

2.4.2 Else set m

:= m, m := (m

+ m

)/2.

3. Return ⌊m

⌋.

Figure 5: Algorithm A

′

algorithm A

′

requires now four precision parameters

,δ

,ε

,δ

, see the Fig. 5.

The result of A

′

is quantity compliant with the fol-

lowing deﬁnition (and is an estimation of the true VC-

dimension).

Deﬁnition 7. We say that the probabilistic

(ε

,δ

,ε

,δ

)-VC-dimension for the set F equals m,

we write

VCdim

,δ

,ε

,δ

(F) = m,

if there exists a sample of size z

,...,z

such that with

probability at least 1− δ

,...,z

) ≥ 1− ε

(23)

and with probability at least 1− δ

(m+ 1) ≤ ε

. (24)

Putting it in simpler wording, the probabilistic

(ε

,δ

,ε

,δ

)-VC-dimension is m if we can indicate

a sample of size m for which with high probability

all dichotomies are feasible, and simultaneously with

high probability we cannot indicate such sample of

size m + 1. Obviously, both probability parameters

refer strictly to quantities µ and η, which one should

be aware of. They are related to different probabilistic

spaces. The probability 1 − δ

and µ quantities refer

to the probabilistic space with P distribution, whereas

the probability 1 − δ

and η quantities refer to the

probabilistic space describing feasibility of random

dichotomies drawn uniformly from {0, 1}

for some

ﬁxed sample z

,...,z

Please note that, in contrast to the algorithm A, the

result of A

′

can be (with small probability)both under-

estimation and overestimation of the true VCdim(F).

ICAART 2012 - International Conference on Agents and Artificial Intelligence

268

It is worth remarking that the algorithm B

′

is of

constant complexity O(N) where N = − lnδ

/(2ε

Therefore, it is easy to see that the complexity of the

′

algorithm is



−lnδ

2ε

−lnδ

2ε

log

∗



. (25)

6.1 Notes on Distribution of Results for

Algorithm A

′

Having in mind the theorem 1 which describes the

probability distribution p(h) of results to which the

algorithm A may converge, we can try to do a sim-

ilar analysis for the A

′

algorithm. The main differ-

ence now is that A

′

can overestimate the true VC-

dimension. This happens when for some sample

drawn in the step 2.2.1. some dichotomies are not fea-

sible, but B

′

fails to discover it in its N trials. In other

words, apart from quantities µ

(m) the involvement

of η

,...,z

) must be taken into account.

Consider the following expectation



[#(l

)

,...,z

= 2

]

+ [#(l

)

,...,z

< 2

]η

,...,z

)



,...,z

)

= µ

(m)

[#(l

)

,...,z

< 2

]η

,...,z

)

,...,z

). (26)

It describes (in an average case) the probability of an

event of interest, i.e. : that either a randomly drawn

sample of size m can be shattered (ﬁrst summand) or

it cannot be shattered, but this fact was not discovered

in N trials (second summand). Therefore, to explicitly

write down the theoretical probability distribution for

results of A

′

it is sufﬁcient to insert into (17) quantities

in the place of µ

7 SUMMARY AND FUTURE

RESEARCH

In the paper we propose a general idea for probabilis-

tic estimation of the VC-dimension for an arbitrary

set of indicator functions. The idea required suitable

deﬁnitions of several notions and quantities which can

be regarded as probabilistic counterparts of some tra-

ditional notions deﬁned by Vapnik.

The main idea is based on an approach we call

expand or divide and conquer and is represented

by two algorithms A and A

′

that we propose. The

analysis of computational complexity shows that A

′

requires only logarithmic time with respect to the

true VC-dimension it tries to discover. This time

scales also with imposed precision parameters: n =

−lnδ

/(2ε

)

, N = − lnδ

/(2ε

)

, and their scaling

inﬂuence on the time is O(n· N).

We are aware that the presented part of research

constitutes only the theoretical part. Certainly, practi-

cal applications of the idea may still require a thor-

ough experimental research ﬁrst, possibly some re-

ﬁnements in algorithms, in order to be successful.

In the future, we plan to carry out the following

experimentally-oriented studies on the idea:

1. executions of A and A

′

on sets of functions with

simple geometrical bases (hyperplanes, spheres,

rectangles etc.),

2. tests for linear combinations of bases,

3. tests for sets of functions with regularization,

4. tests on convergence and performance,

5. registering histograms of experimental distribu-

tions of results to see how heavy are the tails

(i.e. how often under/overestimations of the true

VC-dimension occur),

6. discovering ‘good’ settings for precision parame-

ters for given conditions of experiment,

7. tests for sets of functions for which the true VC-

dimension is unknown.

Results of these studies ought to form a separate pub-

lication.

ACKNOWLEDGEMENTS

This work has been ﬁnanced by the Polish Govern-

ment, Ministry of Science and Higher Education from

the sources for science within years 2010–2012. Re-

search project no.: N N516 424938.

REFERENCES

Anthony, M. and Bartlett, P. (2009). Neural Network Learn-

ing: Theoretical Foundations. Cambridge University

Press, Cambridge, UK.

Bartlett, P., Kulkarni, S., and Posner, S. (1997). Covering

numbers for real-valued function classes. IEEE Trans-

actions on Information Theory, 47:1721–1724.

Cherkassky, V. and Mulier, F. (1998). Learning from data.

John Wiley & Sons, inc.

PROBABILISTIC ESTIMATION OF VAPNIK-CHERVONENKIS DIMENSION

269

Graham, R., Knuth, D., and Patashik, O. (2002). Con-

crete Mathematics. A foundation for Computer Sci-

ence. Wydawnictwo Naukowe PWN SA, Warsaw,

Poland.

Hellman, M. and Raviv, J. (1970). Probability of error,

equivocation and the chernoff bound. IEEE Transac-

tions on Information Theory, IT-16(4):368–372.

Papadimitriou, C. and Yannakakis, M. (1996). On limited

nondeterminism and the complexity of the V-C di-

mension. Journal of Computer and System Sciences,

53:161–170.

Schmidt, J., Siegel, A., and Srinivasan, A. (1995).

Chernoff-hoeffding bounds for applications with lim-

ited independence. SIAM Journal on Discrete Mathe-

matics, 8(2):223–250.

Vapnik, V. (1995). The Nature of Statistical Learning The-

ory. Springer Verlag, New York.

Vapnik, V. (1998). Statistical Learning Theory: Inference

from Small Samples. Wiley, New York.

Vapnik, V. and Chervonenkis, A. (1968). On the uniform

convergence of relative frequencies of events to their

probabilities. Dokl. Aka. Nauk, 181.

Vapnik, V. and Chervonenkis, A. (1989). The necessary

and sufﬁcient conditions for the consistency of the

method of empirical risk minimization. Yearbook of

the Academy of Sciences of the USSR on Recognition,

Classiﬁcation and Forecasting, 2:217–249.

Wenocur, R. and Dudley, R. (1981). Some special Vapnik-

Chervonenkis classes. Discrete Mathematics, 33:313–

318.

Zhang, T. (2002). Covering number bounds of certain reg-

ularized linear function classes. Journal of Machine

Learning Research, 2:527–550.

ICAART 2012 - International Conference on Agents and Artificial Intelligence

270